大跨径预应力混凝土连续刚构箱梁桥荷载试验研究

■池毓伟

（福建省交通建设工程试验检测有限公司，福州350008）

大跨径预应力混凝土连续刚构箱梁桥荷载试验研究

■池毓伟

（福建省交通建设工程试验检测有限公司，福州350008）

本文以一座新建的大跨径某海峡大桥的通航主桥预应力混凝土连续刚构箱梁桥为例，对其荷载试验进行研究。研究结果表明，在试验荷载作用下，测试截面的应变、挠度的校验系数及相对残余变形均满足“规程”要求；桥梁的实测自振频率大于理论计算值，实测振型与理论振型基本一致；冲击系数小于理论计算值；满足公路-I级设计荷载等级要求。

静动载预应力连续刚构箱梁试验研究

0 前言

箱梁结构由于抗弯与抗扭性能优越以及施工方便等特点，在桥梁建设中被广泛采用。目前，桥梁结构荷载试验是检验桥梁承载能力最直接、最有效的方法，荷载试验分为静载试验和动载试验，通过桥梁静动载试验及其对试验数据的综合分析研究，判断桥梁结构是否满足设计要求，为工程验收质量评价提供技术支持，也为桥梁后期养护管理提供依据。本文以某新建的大跨径海峡大桥的通航主桥预应力混凝土连续刚构箱梁桥为工程案例，对其荷载进行试验研究。

1 工程背景

某海峡大桥的通航主桥上部结构为四跨（100+2× 180+100m）变高度预应力混凝土连续刚构箱梁。通航孔（K43+526.235m～K44+086.235）为双孔单向航道，代表5000吨级海轮为标准。桥跨布置为100+2×180+100m，全长560m。下部结构采用钻孔桩基础。桥面横向由一个单箱单室直腹板箱梁组成，箱梁顶板宽17m，底板宽8.5m，两悬臂长4.25m。桥面由箱梁中心线向两侧设置1.5%双向横坡。箱梁根部箱中心梁高11m（高跨比约1/16.36），跨中及边跨现浇直线段箱中心梁高3.5m（高跨比约1/ 51.43），其间梁底曲线以1.6次抛物线变化。行车道数为三车道。设计荷载：公路-Ⅰ级。详见图1～图2。

图1 某海峡大桥示意图

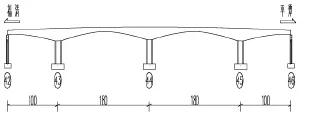
图2 某海峡大桥通航主桥立面图（单位：m）

2 静动载试验

2.1 静载试验

2.1.1 静载试验原则

为使静载试验达到既定目的，试验按以下原则：

（1）为使荷载试验能充分反映桥梁结构受力特点，静载试验效率不宜过小，否则，不能反映出桥梁在设计荷载下的工作性能；同时，也不宜过大，以防结构局部破坏，因此，根据《公路桥梁荷载试验规程》（JTG/T J21-01-2015）（以下简称“规程”）的规定，对交（竣工）验收荷载试验效率控制在0.85～1.05之间。否则，应控制在0.95～1.05之间。

（2）静载试验宜对结构的内力、应力、位移和裂缝的控制截面进行；按桥梁结构的最不利受力原则和代表性原则确定试验工况及测试截面。

（3）正式加载试验前，应对加载桥梁进行预加载，使结构状态能进入正常工作状态。同时检查整个试验及测试系统能否正常进行。

（4）试验荷载应分级施加，若结构变位或应变较大，应实时绘制测点变位或应变与荷载的关系曲线，分析结构状态，确保结构安全。加载级数应根据试验荷载总量和荷载分级增量确定，可分成3～5级，当桥梁资料不全时，应增加分级。

（5）加载时间间隔应满足结构反应稳定的时间要求，待前一级荷载阶段内结构反应相对稳定后，方可进入下一级荷载试验。当进行主要控制截面最大内力（变形）加载试验时，分级加载稳定时间不少于5min；对尚未投入运营的新桥，首个工况的分级加载稳定时间不宜少于15min。

（6）试验过程中发生下列情况时，应立刻停止加载并查找原因，采取措施后再确定是否进行试验，并在确保结构及人员安全的情况下方可继续试验。

①控制测点应变值已经达到或超过计算值。②控制测点变形（挠度）已超过计算值。

③结构的裂缝长度、宽度或数量明显增加。④实测变形分布规律异常。

⑤桥体发出异常响声或发生其他异常情况。

2.1.2 有限元计算模型

采用MIDAS/Civil大型有限元程序计算软件建立空间模型，某海峡大桥的通航主桥有限元计算模型见图3。在设计荷载作用下，结构的内力包络图见图4～图5。

图3 有限元计算模型图

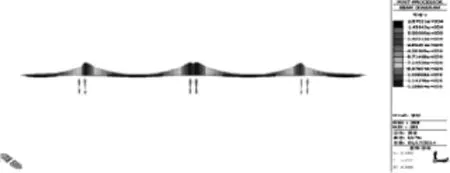
图4 活载弯矩包络图

图5 活载剪力包络图

2.1.3 试验工况

选择测试截面时，应依据桥跨结构所得的内力包络图，并考虑应力分布，按最不利受力原则进行选定。依此原则选择了第44#墩支点负弯矩（III-III）截面、第45跨跨中最大正弯矩（II-II）截面以及第46跨最大正弯矩（I-I）截面进行试验。具体见表1，该桥梁测试截面如图6。

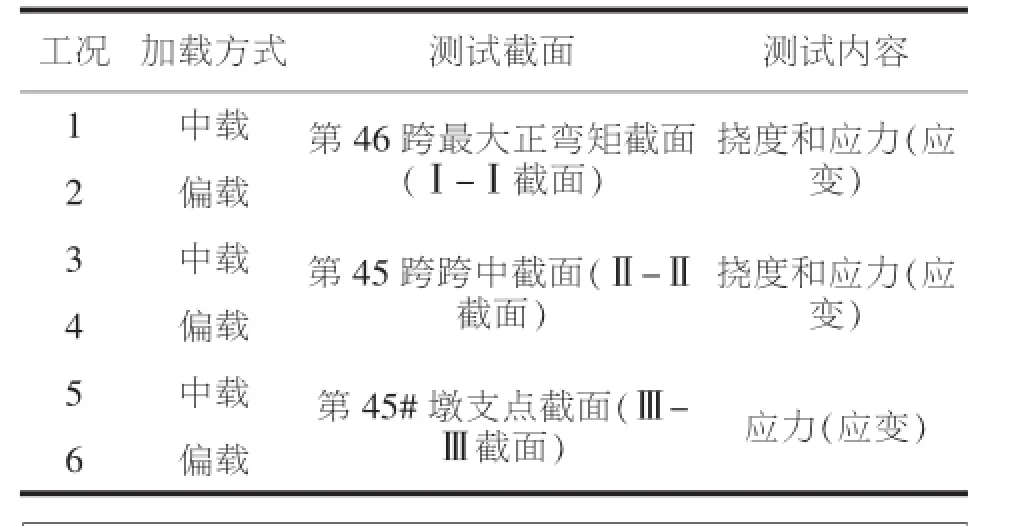
表1 静力试验加载工况一览表

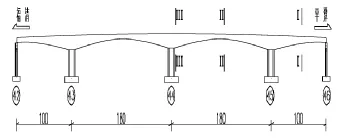
图6 测试截面示意图（单位：m）

2.1.4 静载试验效率

经计算分析确定的各工况控制截面，采用有限元结构分析软件MIDAS/Civil进行控制截面内力影响线分析，根据程序计算所得的设计荷载作用下桥跨结构的各控制截面处最大弯矩影响线见图7～图9。根据影响线分析结果进行加载，以设计标准活载产生的该试验项目的最不利效应值等效换算，确定所需的试验荷载、加载车辆和轮位。本试验桥跨静载试验共采用12辆三轴重型（340kN）车辆进行等效加载。限于篇幅，仅列出横桥向中载车辆加载布置图（见图10）。由表2可知静力荷载试验效率（η）为0.98～1.00，满足了“规程”中所规定的交（竣）工验收荷载试验0.85≤η≤1.05的限值要求，说明静载试验能充分反映桥梁结构受力性能。

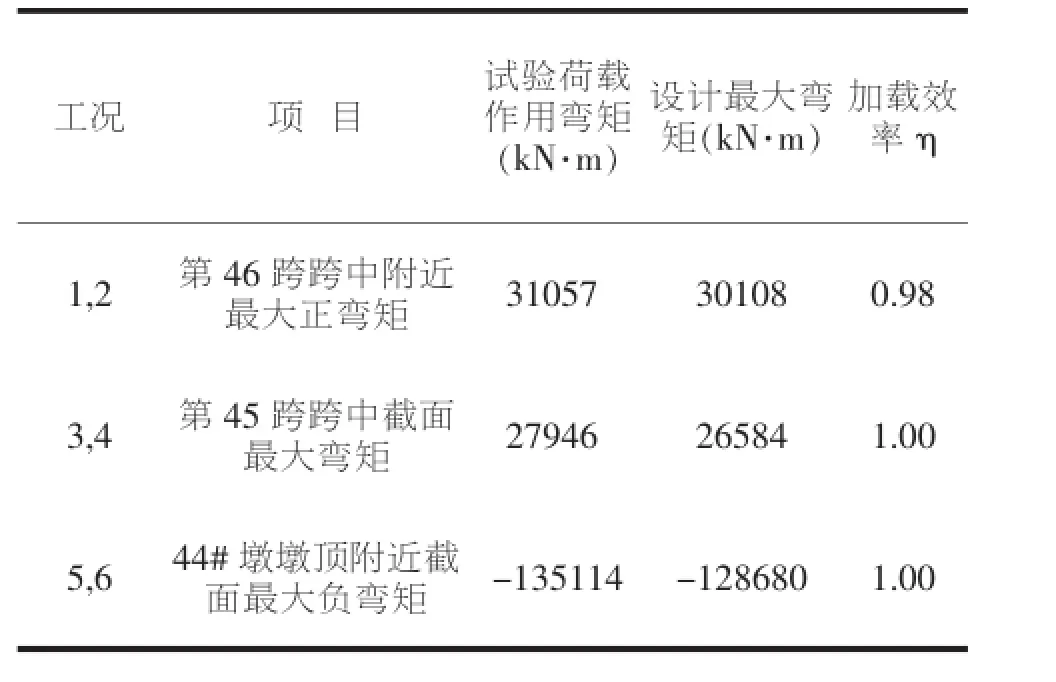
表2 静力试验荷载效率计算一览表

图7 第46跨最大正弯矩影响线图

图8 第45跨中点处弯矩影响线图

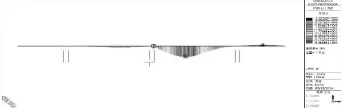
图9 第44号墩墩顶处弯矩影响线图

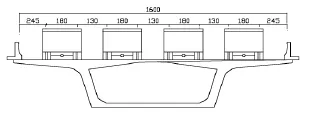
图10 横桥向中载车辆加载布置示意图（单位：cm）

2.1.5 测点布置

I、II、III测试截面应变测点布置如图11～图13，每个截面箱内布设14～16个电阻应变片测点，用静态数据采集仪进行测试；挠度测点布设在位于桥面左、右两侧I-I、II-II截面（见图14），用精密水准仪测量。

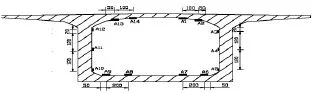
图11 I-I截面应变测点布置图

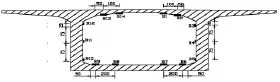
图12 II-II截面应变测点布置图

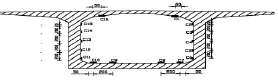
图13 III-III截面应变测点布置图

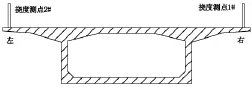
图14 各控制截面挠度测点布置图

2.2 动载试验

2.2.1 动载试验原则

（1）桥梁动载试验测试截面应根据桥梁结构振型特征和行车动力响应最大的原则确定。

（2）对多联（孔）桥梁，同时开展静、动载试验时，动载试验桥联（孔）与静载试验相同。

（3）脉动测点一般根据桥梁结构按跨径8等分或16等分简化布置。

（4）宜首选无障碍行车试验。有障碍行车和制动试验根据实际情况选择。

（5）无障碍行车试验荷载效率ηd宜取高值，但不超过1。

（6）正式试验前应进行预加载试验，对测试系统进行稳定性检查。

2.2.2 自振特性试验

在桥面无任何交通荷载以及桥址附近无规则振源的情况下，采用环境随机振动法测定桥跨结构由于桥址处风荷载、地脉动等随机荷载激振而引起的桥跨结构微幅振动响应，以测定桥梁结构的自振特性。在各桥跨桥面上8等分及墩顶处放置脉动测点传感器，用DH5922N智能信号自动采集仪和DHMA实验模态分析系统软件进行数据采集与分析，从而得到分析桥梁结构的频率、振型、阻尼比等自振特性参数。

2.2.3 无障碍行车试验

在桥面无障碍的情况下，采用1辆载重汽车（单车总重约34t）分别以车速20km/h、30km/h和40km/h匀速通过桥跨结构，应用DH5922动力测试系统测试第45跨跨中截面的动应变，分析其冲击系数。动应变测点布于第45跨跨中截面。

3 静动载试验结果与分析

3.1 静载试验结果与分析

3.1.1 桥梁静载试验数据分析

（1）校验系数

校验系数η是评定结构受力状况，确定桥梁承载能力的一个重要指标。实测结构校验系数·是试验的实测值与理论计算值的应力或挠度之比，它反映结构的实际工作状态。

同类型桥梁η值越小,说明结构的安全储备越大，但η值不宜过大或过小，如η值过大可能因为组成结构的材料强度或弹性模量较低，结构各部分联结性能较差，刚度较低等。η值过小可能因为组成结构材料的实际强度或弹性模量较高，桥面铺装及人行道等与主梁共同受力，以及计算理论或简化的计算图式影响等。另外，试验加载物的称量误差、仪表的观测误差等对η值也有一定的影响。实测结构校验系数η的常值见表3。

表3 实测结构校验系数的常值表

（2）相对残余变位（或应变）

残余变位（或残余应变）按下列公式计算：

总变位（或总应变）St＝Sl－Sh

弹性变位（或弹性应变）Se＝Sl－Su

残余变位（或残余应变）Sp＝St－Se＝Su－Sh

式中，Sh——加载前测值；

Sl——加载达到稳定时测值；

Su——卸载后达到稳定时测值。

相对残余变位（或应变）按下式计算：

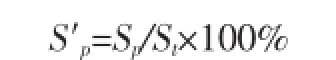
式中，S′p——相对残余变位（或应变），Sp、St意义同前。

测点在控制荷载工况作用下的相对残余变位Sp/St越小，说明结构越接近弹性工作状况。一般要求Sp/St值不大于20%，当Sp/St大于20%时，说明桥梁结构弹性工作状态较差，应查明原因。必要时再次进行荷载试验确定。

（3）裂缝

在试验荷载作用下新桥裂缝宽度不超过《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定的容许值，卸载后其扩展宽度应闭合到容许值的1/3。

3.1.2 挠度试验结果与分析

根据对所观测挠度数据进行整理，限于篇幅，表4仅以列出工况3～4的测试结果。由表4可知挠度理论值与实测值变化规律基本一致，测试截面的挠度校验系数在0.81～0.90之间，均符合“规程”中预应力混凝土桥规定0.70～1.00的常值范围内。最大相对残余变形为6.6%，也小于“规程”规定的20%的限值要求。试验结果表明，桥梁实际状况要好于理论状况，桥梁结构刚度性能良好，其桥梁结构接近弹性工作状况。

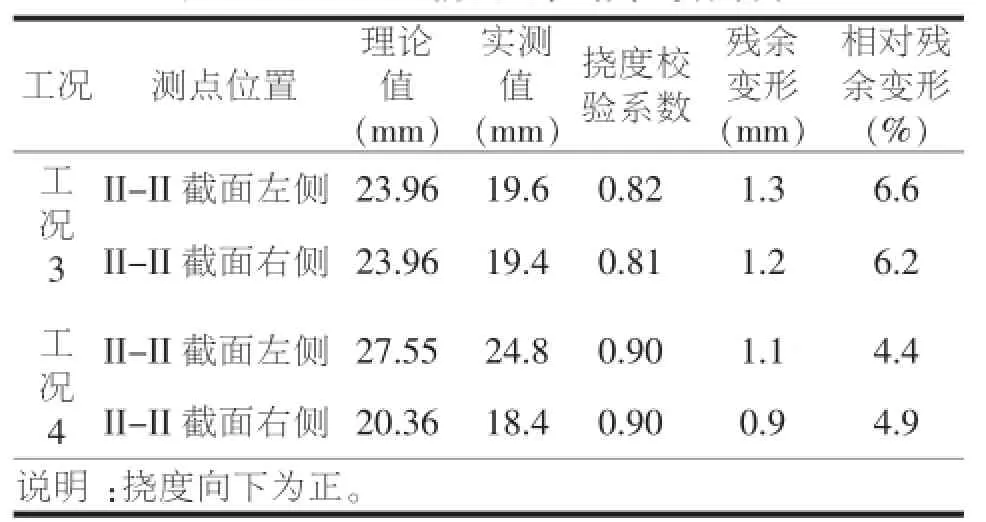
表4 工况3～4挠度试验结果与分析表

3.1.3 应变试验结果与分析

根据对所测应变数据进行整理，限于篇幅，表5仅以列出工况3～4的测试结果。由表5可知应变实测值与理论值变化规律基本一致，测试截面的应变校验系数在0.76～0.88之间，均符合“规程”中预应力混凝土桥规定0.60～0.90的常值范围内。最大相对残余应变为12.5%，也小于“规程”规定的20%的限值要求。试验结果表明，桥梁实际状况要好于理论状况，桥梁结构力学性能良好，桥梁结构接近弹性工作状况。

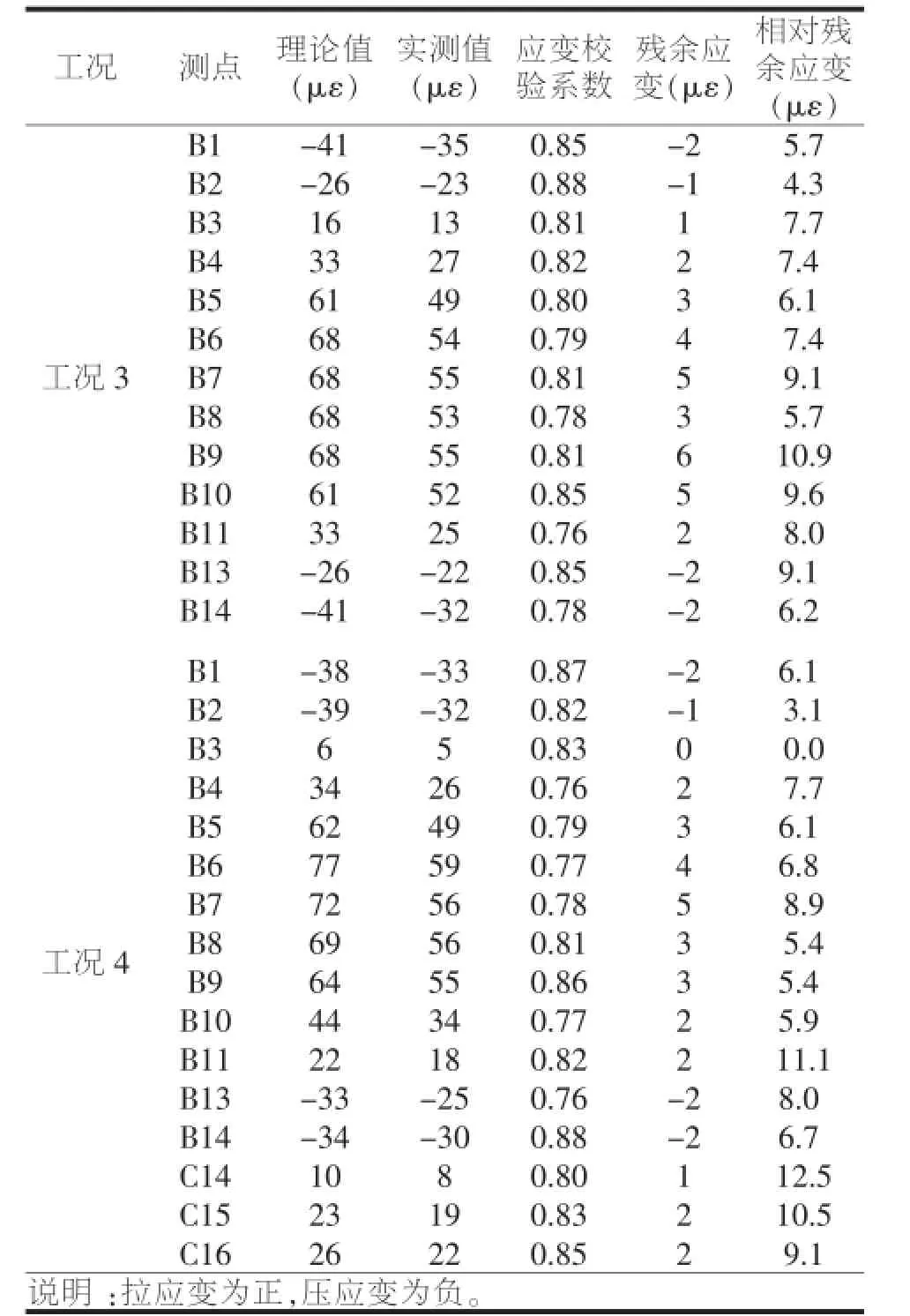
表5 工况3～4应变试验结果与分析表

3.1.4 裂缝观测结果

测试截面及附近没有出现裂缝和其它异常现象。

3.2动载试验结果与分析

动载试验以主要动力测试参数说明结构的动力性能和结构响应，在实测值与理论值对比的基础上对结构做出评价。

3.2.1 自振特性试验结果与分析

现场采集的信号经FFT分析、模态分析，得到该桥第45跨跨中测点时域波形图及频谱图见图15，实测竖向第一阶、二阶自振频率及振型见图16、图18；理论计算竖向第一阶、二阶自振频率及振型见图17、图19；理论计算频率与实测频率参数表见表6。试验表明，该桥实测竖向第一阶、二阶自振频率分别为1.00Hz、1.29Hz，均分别大于竖向第一阶、二阶自振频率理论值0.98Hz、1.17Hz，说明桥梁实际刚度大于理论刚度；竖向实测振型与理论振型一致，表明该桥有限元分析模型中采用计算式基本合理。

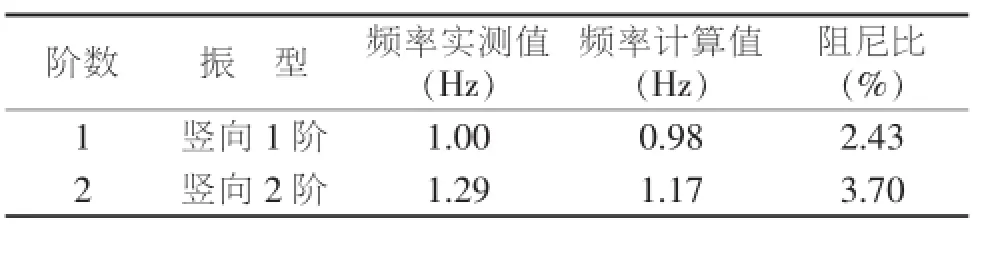
表6 理论计算频率与自振特性参数表

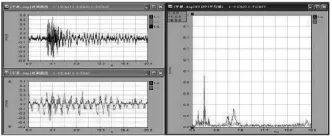
图15 第45跨跨中测点时域波形图及频谱图

图16 实测竖向第一阶自振频率及振型图（自振频率f1=1.00Hz）

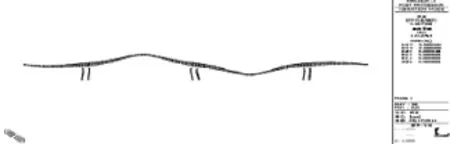
图17 理论计算模型竖向第一阶自振频率及振型图（自振频率f1=0.98Hz）

图18 实测竖向第二阶自振频率及振型图（自振频率f2=1.29Hz）

图19 理论计算模型竖向第二阶自振频率及振型图（自振频率f2=1.17Hz）

3.2.2 无障碍行车试验结果与分析

根据理论计算得到竖向第一阶自振频率0.98Hz，以及《公路桥涵设计通用规范》（JTG D60-2015）中的规定，计算得到该桥冲击系数理论计算值为1.05。经动力测试系统信号采集和分析，该桥在无障碍行车情况下的桥梁动应变与冲击系数列于表7。限于篇幅，仅绘出40km/h车速时动应变时程曲线（见图20）。该桥经换算标准汽车荷载作用下的冲击系数最大值为1.02，小于理论计算值1.05，表明该桥有较好的抗动载冲击能力。

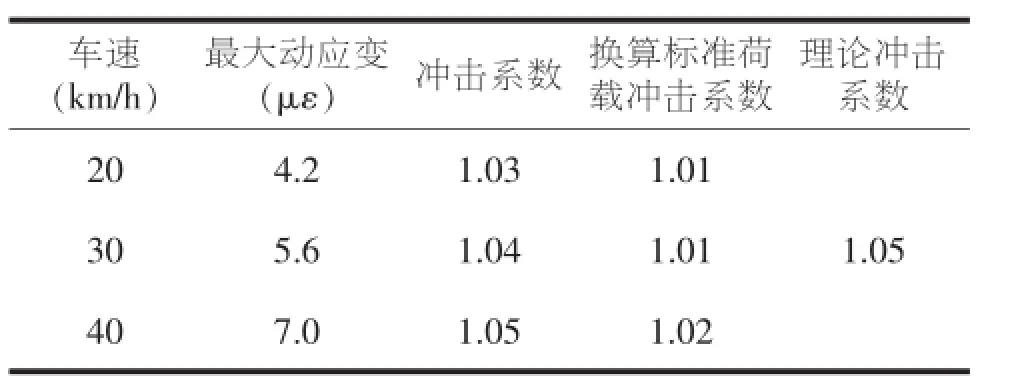
表7 不同车速激振下桥面动应变与冲击系数

图20 40km/h车速时动应变时程曲线图

4 结论

通过对该桥荷载试验以及对试验数据并结合试验现象进行综合分析研究，结论如下：

（1）静载试验效率系数介于0.98～1.00之间，符合“规程”规定。表明试验荷载能反映设计荷载对桥梁结构的作用，试验结果有效。

（2）静载试验结果研究表明：在试验荷载作用下，桥跨结构各测试截面挠度和应变校验系数，分别介于0.81～0.90、0.76～0.88之间，均符合“规程”中预应力混凝土桥规定的常值范围内，桥梁实际状况要好于理论状况,桥跨结构受力性能良好；最大相对残余变形和应变分别为6.6%、12.5%，均低于“规程”规定值20%的要求，桥梁实际状况要好于理论状况，桥梁结构刚度性能良好，接近弹性工作状况。

（3）动载试验结果研究表明：实测竖向第一阶、二阶自振频率分别为1.00Hz、1.29Hz，均分别大于竖向第一阶、二阶自振频率理论值0.98Hz、1.17Hz，说明桥梁实际刚度大于理论刚度；竖向实测振型与理论振型基本一致，表明该桥有限元分析模型中采用计算式基本合理。该桥经换算标准汽车荷载作用下的冲击系数最大值为1.02，小于理论计算值1.05，表明该桥有较好的抗动载冲击能力。

（4）裂缝观测结果表明，测试截面及附近没有出现裂缝和其它异常现象。

（5）综上所述，该桥满足公路-I级设计荷载等级要求。

[1]JTG/TJ21-01-2015,公路桥梁荷载试验规程[S].

[2]何玉珊，程崇国，章关永，涂耘.桥梁隧道工程[S].北京：人民出版社股份有限公司.2016.5.

[3]MIDAS/Civil分析与计算原理[S].北京：迈达斯技术有限公司. 2016.5.

[4]张玉平,李传习.株洲建宁大桥斜拉桥静载试验研究[J].公路与汽运，2008（2）.