计算B3-型量子群的Gröbner-Shirshov基*

阿布力米提·孜克力亚, 杨 凡, 齐秀琴, 马 丽

(新疆农业大学 数理学院,乌鲁木齐 830052)

计算B3-型量子群的Gröbner-Shirshov基*

阿布力米提·孜克力亚, 杨 凡, 齐秀琴, 马 丽

(新疆农业大学 数理学院,乌鲁木齐 830052)

为了计算出B3型量子群的Gröbner-Shirshov基，先用有限维代数表示论中的Auslander-Reiten理论和Hall代数方法计算出B3型量子代数根向量之间的拟交换关系式并验证这些关系式对合成运算封闭，然后给出B3型量子群的一个极小Gröbner-Shirshov基.

量子群；Gröbner-Shirshov；拟交换关系

文献[1-5]中介绍了代数学中特别有用的工具——约化问题(Gröbner-Shirshov基理论).在文献[4]中作者给出了构造量子包络代数的Gröbner-Shirshov基的方法后,人们按照此方法分别计算并构造了3个不同(E6,F4,G2)量子包络代数的Gröbner-Shirshov基[5-7].

本文先用文献[8]中提出的Frobenius映射方法算出B3型量子代数的3个根向量之间的拟交换关系，再用Ringel介绍的同构理论来构造出B3型包络代数的正部分和负部分的Gröbner-Shirshov基,最后用文献[4]中的方法构造出了整个B3型包络代数的极小Gröbner-Shirshov基.

1 准备知识

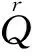
M=M0⊇M1⊇…⊇Mt-1⊇Mt=0

其中

≅Ni(对所有1≤i≤t)

(dimM,dimN)=〈dimM,dimN〉+〈dimN,dimM〉

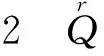
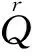
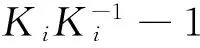
其中：

(f,g)ω≡0 mod (S;ω)

2 B3-型量子包络代数的Gröbner-Shirshov基

如图1所示，先选取B3的如下定向：

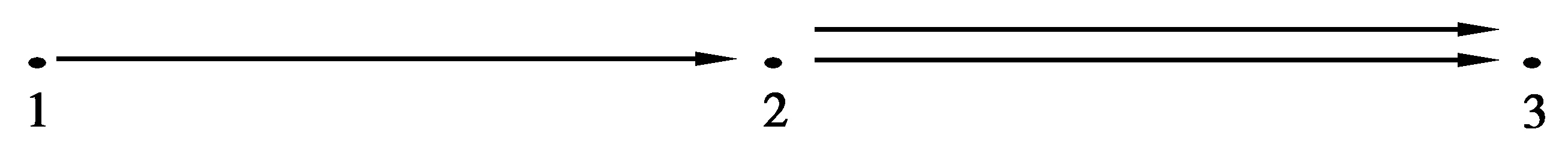
图1 B3的Dynkin赋值图
Fig.1 Dynkin assignment chart of B3

图1是B3的Dynkin赋值图及对应的极小对称化子，D和Cartan矩阵A分别为

,

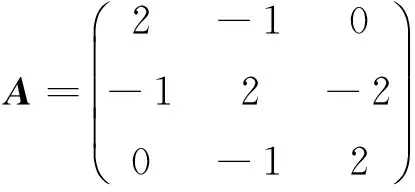
U≅U+⊗U0⊗U-

B3的Auslander-Reiten箭图如图2所示.

图2 B3的Auslander-Reiten箭图Fig.2 Auslander-Reiten arrow chart of B3

图2中,向上箭头↗的权值为(1,2),向下箭头↘的权值为(2,1).设

因为e1,e2,和e3分别是对应于点1,2和3的单模,所以

X1=[e3],X7=[e2],X9=[e1]

令E3=η-1(X1),E233=η-1(X2),E23=η-1(X3)

E1233=η-1(X4),E12233=η-1(X5),E123=η-1(X6)

E2=η-1(X7),E12=η-1(X8),E1=η-1(X9)

和X={E1,E2,E3,E12,E12233,E123,E1233,E23,E223}

选取以下序：

E3>E23>E223>E2>E1233>

E123>E12233>E12>E1

这里的序是单项式集上的一个字典排序,

1≤i≤9}

是Uq(B3)的一组单项式集[9].

为了计算出一切拟交换关系，首先计算较容易的以下18个关系式：

E3E1=E1E3

(1)

E2E123=E123E2

(2)

E23E123=E123E23

(3)

E233E3=υ2E3E233

(4)

E1233E3=υ2E3E1233

(5)

E23E233=υ2E233E23

(6)

E1233E233=υ2E233E1233

(7)

E12233E23=υ2E23E12233

(8)

E2E23=υ2E23E2

(9)

E12233E1233=υ2E12233E1233

(10)

E123E1233=υ2E123E1233

(11)

E1E1233=υ2E1233E1

(12)

E123E12233=υ2E12233E123

(13)

E2E12233=υ2E12233E2

(14)

E12E123=υ2E123E12

(15)

E1E123=υ2E123E1

(16)

E12E2=υ2E2E12

(17)

E1E12=υ2E12E1

(18)

其次，通过计算两个不可分解模之间的Hom空间和Ext空间的维数得到以下公式：

E2E3=υ-2E3E2+E23

(19)

E12E3=υ-2E3E12+E123

(20)

E1E233=υ-2E233E1+E1233

(21)

E2E1233=υ-2E1233E2+E12233

(22)

E1E2=υ-2E2E1+E12

(23)

E1E23=υ-2E23E1+E123

(24)

最后,“归纳”上面关系式得到剩下的公式：

E23E3=E3E23+(υ+υ-1)E223

(25)

E123E3=E3E123+(υ+υ-1)E1233

(26)

E123E23=E23E123+(υ+υ-1)E12233.

(27)

E12233E3=E3E12233+(υ2-υ-2)E23E1233

(28)

E12E23=E23E12+(υ2-υ-2)E123E2

(29)

E123E233=E233E123+(υ2-υ-2)E1233E23

(30)

(31)

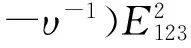
(32)

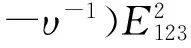
(33)

(34)

(35)

E12E233=υ-2E233E12+(2υ-1-υ+υ-3)E123E23+(υ-4-υ-2-1)E12233-υ-4E1233E2

(36)

下面给式(36)的推导过程说明所说的“归纳”法,式(22)的两边乘E1得到：

E1E2E233=υ-2E2E1E233+E12E233

(37)

对式(37)用式(31),式(20)得到：

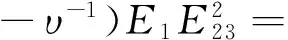
υ-4E2E233E1+υ-2E2E1233+E12E233

υ-4E2E233E1+υ-2E2E1233+E12E233

再分别用式(23),式(27)得到：

υ-2E12233+E12E233=

υ-4E233[υ2(E2E1-E12)] +

(υ-3-υ-5)E23[υ2(E1E23-E123)] +

υ-4E123E2+υ-2E12233+E12E233

最后等式两边整理得到：

E12E233=υ-2E233E12+(2υ-1-υ+υ-3)E123E23+

(υ-4-υ-2-1)E12233-υ-4E1233E2

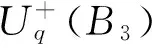
那么就有S+⊆S+c.显然,里面的单项式都不可约，因此根据文献[3]中的钻石引理,得到以下结果.

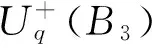
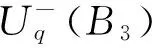
F1=ω(E1)

F2=ω(E2)

F3=ω(E3)

F12=ω(E12)

F123=ω(E123)

F1233=ω(E1233)

F12233=ω(E12233)

F23=ω(E23)

F223=ω(E223)

那么就得到关于子代数Uq(B3)-的生成元：

Y={F1,F2,F3,F12,F12233,F123,F1233,F223,F23}

用R′(1)来表示关于Fij的以上关系的集合.显然R′(1)包含定义关系集S-,因此如果J是由R′(1) 生成的理想,那么Uq(B3)-可以看成商代数Q(υ)〈Y>/J.

选取序

F3>F23>F223>F2>F1233>

F123>F12233>F12>F1

则此序单项式集的一个字典排序.同样，用S-c(1≤i≤36)来表示R′(1)中的多项式,令

S-c={ω

那么就有S-⊂S-c，同理得到以下定理.

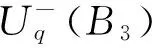
如果选取序

E3>E23>E223>E2>E1233>E12233>

E3>F23>F223>F2>F1233>

F12233>F12>F1

这时根据文献[4]中的定理，叙述下面主要结论.

定理3 量子包络代数Uq(B3)的极小Gröbner-Shirshov基是集合S-c∪K∪T∪S+c.

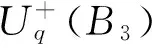
[1] BUCHBERGER B. An Algorithm for Finding a Basis for the Residue Class Ring of a Zero-Dimensional Ideal[M].Innsbruck:University of Innsbruck,1965

[2] BERGMAN G M. The Diamond Lemma for Ring Theory[J].Advances in Mathematics,1978,29(3):178-218

[3] SHIRSHOV A I. Some Algorithmic Problems for Lie Algebras[J].Siberian Mathematical Journal,1962,3(5):292-296

[4] BOKUT L A,MALCOLMSON P. Grobner-Shirshov Basis for Quantum Enveloping Algebras[J].Israel Journal of Mathematical,1996,96(2):97-113

[5] 艾尼·吾司塔,阿布都卡的·吾甫.G2型量子群表示的Gröbner-Shirshov基[J].重庆工商大学学报(自然科学版),2013,11(1):1-5

Aini Utta, Abdukadir Obul.Gröbner-Shirshov Basis Represented by G2-Type Quantum Group[J].Journal of Chongqing Technology and Business University (Natural Science Edition),2013,11(1):1-5

[6] REN Y H,OBUL A. Grobner-Shirshov Basis of Quantum Group of Type G2[J].Comm,Algebra,2011,39(5):1510-1518

[7] QIANG C X,OBUL A. Grobner-Shirshov Basis of Quantum Group of Type F4[J].Frontiers of Mathematics in China,2014,9(1):135-150

[8] OBUL A,YUNUS G. Grobner-Shirshov Basis of Quantum Group of Type E6[J].Journal of Algebra,2011,346(5):248-265

[9] DENG B M,DU J,Parshal B,et al.Finite Dimensional Algebra and Quantum Groups[M].Soc Providence:Mathematical Surveys and Monographs,2008

[10] RINGEL C M. Hall Polynomials for Representation-Finite Hereditary Algebras[J].Advances in Mathematics,1990,84(3):137-178

[11] RINGEL C M. PBW-bases of Quantum Groups[J].Jreine Angew Math,1996,470(7):51-88

责任编辑：罗姗姗

Calculation of Grobner-Shirshov Basis of Quantum Group of TypeB3

Ablmit Zikerya, YANG Fan, QI Xiu-qin, MA Li

(School of Mathematics and Physics, Xinjiang Agricultural University, Urumqi 830052, China)

In order to calculate Grobner-Shishov basis of quantum groupB3, firstly Auslander-Reiten theory and Hall algebraic method in finite dimension algebraic expression are used to calculate skew-commutators between algebraic root vectors of quantum group ofB3, and their composition operation closure of these commutators is tested, then the minimal Grobner-Shirshov basis of the quantum groupB3is given.

quantum group; Grobner-Shirshov; skew commutator

2016-10-13；

2016-11-14.

新疆维吾尔自治区大学生创新创业训练计划项目(201610758186).

阿布力米提·孜克力亚(1987-)，男，新疆乌鲁木齐人，助教，硕士，从事代数表示论研究.

10.16055/j.issn.1672-058X.2017.0002.005

O152.8

A

1672-058X(2017)02-0022-05