求解凸极小化问题的一种部分并行的可分方法

李 小 容

(重庆师范大学 数学科学学院，重庆 401331)

求解凸极小化问题的一种部分并行的可分方法

李 小 容

(重庆师范大学 数学科学学院，重庆 401331)

针对具有可分结构的凸极小化问题，提出了一种部分并行的可分方法.该方法是在预校正近似乘子法的基础之上，在极小化时采取了不同的格式，去掉了二次邻近项而直接用的增广项；在算法的迭代部分，预校正近似乘子法先计算xk+1，再计算zk+1，在部分并行的可分方法中，xk+1，zk+1是并行计算的；通过数值算例得到的结果显示，该方法具有可行性.

凸优化问题；交替方向乘子法；预校正近似乘子法；部分并行的可分方法

本文针对两个变量的可分离凸优化问题进行研究[1]，形式如下：

minf(x)+g(z)

s.t.Ax+Bz=b

(1)

其中：f:Rn→(-∞,+∞]和g:Rn→(-∞,+∞]是闭凸真函数，A是m×n矩阵，B是m×s矩阵，b是m维向量.问题(1)是一种经典的凸规划问题，它广泛应用于信号与图像处理、统计学、机器学习等领域中[2].

问题(1)的拉格朗日函数L：Rn×Rs×Rm→(-∞,+∞]定义如下：

L(x,z,λ)=f(x)+g(z)+〈λ,Ax+Bz-b〉

(2)

问题(1)的增广拉格朗日函数Ψ：Rn×Rs×Rm→(-∞,+∞]定义如下：

Ψc(x,z,λ)=f(x)+g(z)+〈λ,Ax+Bz-b〉+

(3)

其中，〈.,.〉表示内积，λ是约束Ax+Bz=b的相应拉格朗日乘子，c是罚因子.

针对两个变量的可分离凸优化问题，很早以前就有学者进行了研究并取得了一定的成果.1975年，R.Glowinsk[3]和D.Gabay[4]等人针对两个变量的可分离凸优化问题，提出了一种算法，即交替方向乘子法(ADMM).

1994年，Chen和Teboulle[5]针对两个变量的可分离凸优化问题，提出了一种可分方法，即预校正近似乘子法(PCPMM).这种方法不同于交替方向乘子法，它充分利用了邻近点乘子法较好的结构特征，并且在较弱的假设条件下，它收敛到原对偶问题的最优解.

预校正近似乘子法的主要算法如下：

在ADMM算法中，没有对变量进行校正，对于解决两个变量的可分离凸优化问题，这种方法的有效性得到了证实.但是当这种算法直接延伸到n个变量的情形时，其收敛性存在一些缺陷.为了达到算法收敛的目的，对目标函数要求太高，条件太强，利用预校正步骤可以避免这一问题.在PCPMM算法中，采用了预校正步骤，使得在较弱的假设条件下可以满足算法的收敛性.

在上述算法的基础之上，提出了一种部分并行的可分方法(MPCPMM).对预校正近似乘子法做了一些改进，在极小化时采取不同的格式，去掉了二次邻近项而直接用增广项.在算法的迭代部分，ADMM算法与PCPMM算法都是先计算xk+1，再计算zk+1.在部分并行的可分方法(MPCPMM)中，xk+1，zk+1是并行计算的.在算法的证明部分，PCPMM算法采用了鞍点最优性条件，文章用到的假设条件是约束条件，其系数矩阵是满秩的.通过数值算例得到的结果显示，与PCPMM算法相比，该方法具有可行性.

1 部分并行的可分方法(MPCPMM)

为了方便后面进一步叙述，考虑如下凸规划问题(带线性约束、目标函数可分)，形式如下：

minf1(x1)+f2(x2)

s.tA1x1+A2x2=b

(4)

其中，fi:Rn→(-∞,+∞]是闭凸真函数，Ai是m×n矩阵，b是m维向量.为了进一步讨论，做出如下假设：(i) 假设问题的解集是非空的；(ii) 矩阵A1，A2是满秩的.

1.1 方法介绍

步骤2 计算

(5)

(6)

步骤3 乘子更新

(7)

1.2 收敛性证明[6]

〈w-w*,Q(w*)〉≥0,∀w∈W

(8)

在这里，

(9)

∂fi是凸函数fi的次微分算子，它是单调的，所以式(8)(9)是可解的.用w*表示式(8)(9)的解，在假设条件下，解集w*是非空的.

≥0

这等价于

(10)

又由MPCPMM算法的式(5)(7)，有λk+1=pk+1=λk.

(11)

(12)

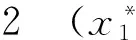
λk-λ*)≥

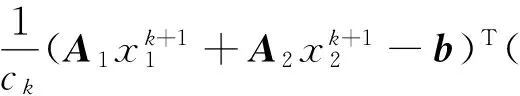
(13)

(14)

(15)

将式(14)(15)加起来，得到

(16)

(17)

同理，可以得到

λk+1-λ*)≥

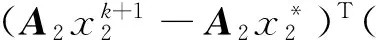
(18)

λk+1-λ*)≥

(19)

由λk+1-λ*=λk-λ*+λk+1-λk及式(7)λk+1的定义，将式(19)进行整理，得到

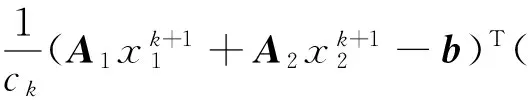
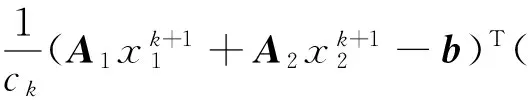
这就完成了证明.

很容易可以看到式(20)(21)是成立的.

(20)

(21)

将式(20)(21)与式(13)相加，可以得到

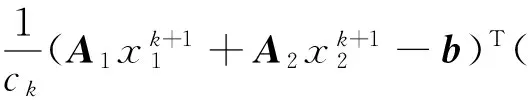
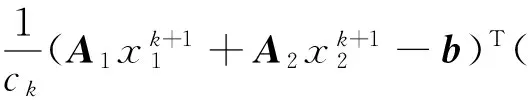
(22)

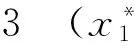
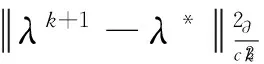
(23)

证明 式(24)—(26)显然成立:

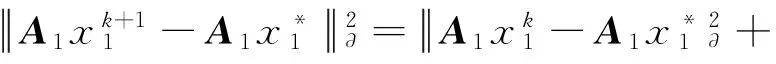
(24)

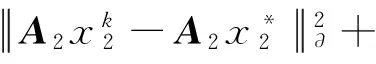
(25)

(26)

由此，可以得到

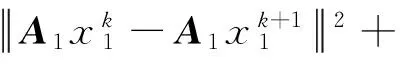
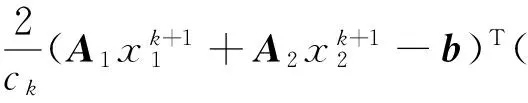
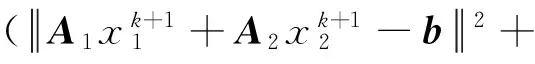
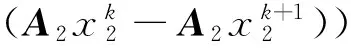
(27)

式(27)可由式(5)(7)(22)得到.对于任意的向量a,b和任意的正参数l>0，有

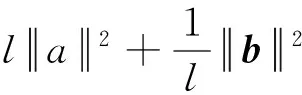
(28)

将式(28)应用到式(27)，就可以得到最后一个不等号成立.因此，引理3得证.

证明 由式(23)，可以推断出：

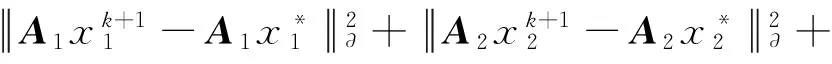
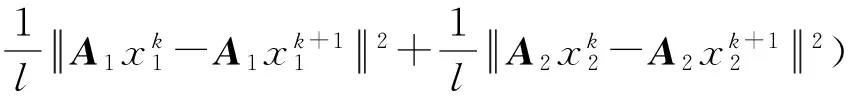
对所有的k(k=0,1,…,∞)求和，可以得到

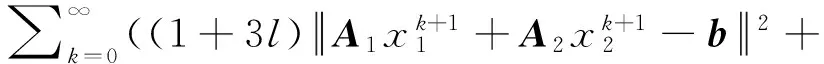
这意味着

(29)

(30)

(31)

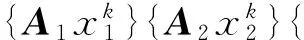
对子序列，将式(11)求极限，可得到

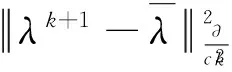
这就完成了证明.

2 数值算例

例1[7]考虑下面的问题

minx2+z2s.t.x-10=-z

这个问题的最优解为x*=5,z*=5,λ*=-10，f(x*，z*)=50，用ADMM，PCPMM，MPCPMM算法求解结果如表1：

表1 例1的数值结果

例2[7]考虑下面的问题：

s.t.

这个问题的最优解为x*=[0.200 0,0.000 0]T，z*=[0.000 0,0.200 0]T，λ*=[-0.080 0,-0.080 0]T，f(x*,z*)=0.08，分别用ADMM，PCPMM，MPCPMM算法求解结果如表2：

表2 例2的数值结果

由以上数值结果显示，MPCPMM算法具有可行性.与PCPMM算法相比，虽然迭代次数和迭代时间上没有明显的优势，但是数值结果相对较好,(x*,z*)和f(x*,z*)更接近最优值.

[1] BOYD S,PARIKH N,CHU E,et al.Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers[J].Foundations and Trends in Machine Learning,2011,3(1):1-122

[2] YANG J,ZHANG Y. Alternating Direction Algorithms for L1-Problems in Compressive Sensing[J].SIAM Journal on Scientific Computing,2011,33(1):250-278

[3] GLOWINSKI R,LETALLEC P.Augmented Lagrangian and Operator Splitting Methods in Nonlinear Mechanics[M].Philadelphia:SIAM Studies in Applied Mathematics,1989

[4] GABAY D,MERCIAR B.A Dual Algorithm for the Solution of Nonlinear Variation Problems via Finite-element Approxi-mations[J].Computers and Mathematics with Application,1975(2):17-40

[5] GONG C,MARC T.A Proximal-based Decomposition Method for Convex Minimization Problems[J].Mathem-atical Programming,1994(64):81-101

[6] HAN D,YUAN X,ZHANG W,et al.An ADM-based Splitting Method for Separable Convex Programming[J].Computational Optimization and Applications,2013,54(2):343-369

[7] 张静.用于预校正乘子法解拟可分多学科设计优化问题[D].重庆:重庆师范大学,2012

ZHANG J.Solve the Quasi-separable MDO Problems by the MPCPMM Method[D].Chongqing:Chongqing Normal University,2012

责任编辑：李翠薇

Partially Parallel of Separable Method to Solve Convex Minimization Problem

LI Xiao-rong

(School of Mathematical Science, Chongqing Normal University, Chongqing 401331, China)

In view of convex minimization problem with separable structure, this paper presents a separable method of partially parallel, and this method is evolved by the predictor-corrector proximal multiplier method. A different format is used in the process of minimization, the quadratic adjacent items are replaced but the augmented items are directly used in the method. Numerical example results show that this method is feasible.

convex optimization problem; alternating direction multiplier method; predictor-corrector proximal multiplier method; partially parallel of separable method

2016-03-15；

2016-04-22.

国家自然科学基金(61263020).

李小容(1991-)，女，重庆巫山人，硕士，从事计算数学研究.

10.16055/j.issn.1672-058X.2017.0002.004

O224

A

1672-058X(2017)02-0016-06