一个修正的NVPRP方法

吴 素 花

(重庆师范大学 数学科学学院,重庆 401331)

一个修正的NVPRP方法

吴 素 花

(重庆师范大学 数学科学学院,重庆 401331)

非线性共轭梯度方法是解决大规模无约束问题最有效的方法之一，提出了一类新的修正共轭梯度算法，新算法推广了黄海东等的共轭梯度参数算法,不依赖任何线搜索且具有充分下降性；然后,在标准 Wolfe非精确线搜索下,得到了新算法的全局收敛性.

无约束优化问题;共轭梯度法;充分下降性;全局收敛性

0 引 言

考虑以下无约束极小问题:

minf(x)x∈Rn

(1)

共轭梯度法是求解这类问题的最有效的方法之一,其一般迭代格式为

xk+1=xk+αkdk

(2)

(3)

其中αk为由某种线搜索确定的步长，gk表示f(x)在点xk处的梯度,参数βk称为共轭梯度参数,关于参数βk的不同取法对应于不同的共轭梯度法.著名的共轭梯度法有1952年Hestenes和Stiefel在文献[1]提出的HS方法；1964年Fletcher和Reevse在文献[2]提出的FR方法；1969年Polak和Ribiere,Polyak在文献[3-4]独立提出的PRP方法；1987年Fletcher在文献[5]中提出的CD方法；1991年Liu和Storey在文献[6]中提出的LS方法； 1999年戴彧虹和袁亚湘在文献[7]提出的DY方法，其对应的βk的计算公式如下：

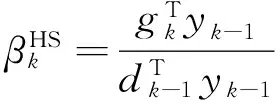
在以上经典的βk公式的选取中，PRP，HS， LS的计算效果比较好,但是理论比较差. 对于一般的非线性函数,Powell[8]举出了一个三维的例子证明了即使采用精确线搜索,PRP方法也不收敛.为了得到好的理论及数值效果,Huang,Li和Wei[9]对PRP方法进行了修正,称为NVPRP方法,βk由下面公式确定：

(4)

江羡珍等在文献[10]中对PRP和HS提出了修正,βk选取如下:

(5)

(6)

基于以上βk的选取,黎小林在文献[11]提出了:

(7)

此处将NVPRP修正如下：

(8)

(9)

其中θ>1,t>1. 记由式(2)(3)(8)确定的方法为MVNPRP方法.

为了得到新方法的全局收敛性,对目标函数进行一般假设:

此处用标准沃尔夫线搜索：

(10)

其中 0<δ<σ<1. 若式(11)成立,则称方法具有充分下降性.

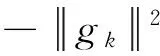
(11)

引理1 对所有θ>2,若gk≠0,对于新方法MNVPRP，总有式(12)成立：

(12)

并且βk≥0.

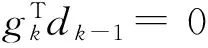
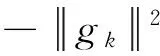
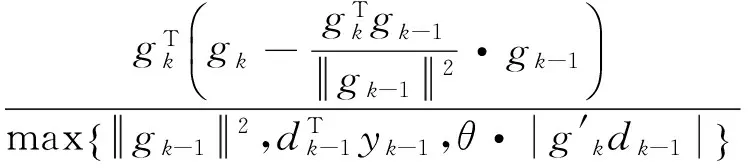
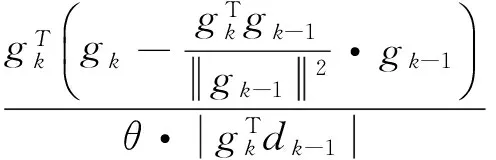
(13)

由式(13)和式(3)可得：

≤

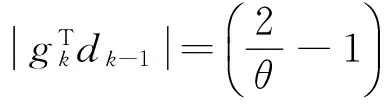
证毕.

引理1说明新方法不依赖线搜索具有充分下降性,下证新方法具有性质1.

性质1 考虑由式(2)(3)和式(8)构成的迭代,假设

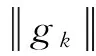
(14)

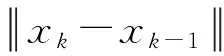
(15)

成立，则称方法具有性质1.

引理2 假设(A1)(A2)成立,由式(2)(3)和式(8)确定的方法在任何线搜索下都具有性质1.

证明 由式(8)和式(13)易得：

0≤βk=

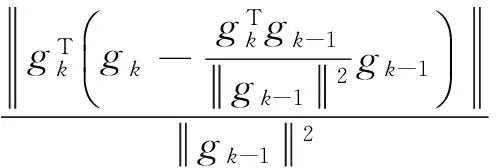
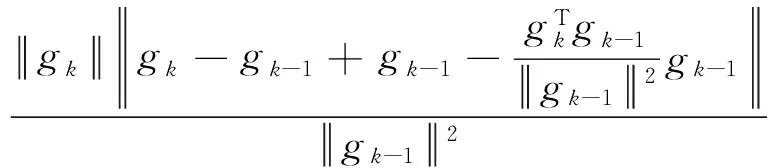
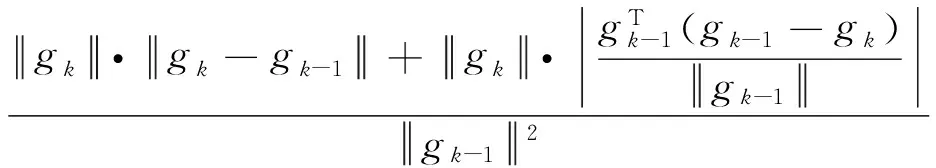
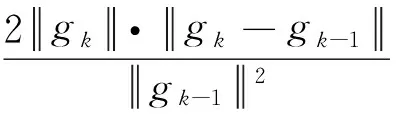
证毕.

因此，由引理1,引理2和文献[12]中定理3.3.3即可得MNVPRP方法的全局收敛性.

定理1 目标函数f(x)满足一般假设(A1)(A2),迭代序列由式(2)(3)产生，αk满足式(10)(11),βk由式(8)确定,则MNVPRP方法全局收敛,即

(16)

同理可证明MNVPRP*方法的全局收敛性.

[1] HESTENES M R,STIEFEL E. Method of Conjugate Gradient for Solving Linear Equations[J].J Res Nat Bur Stand,1952(49):409-436

[2] FLETCHER R,REEVES C M. Function Minimization by Conjugate Gradients[J].The Computer Journal,1964,7(2):149-154

[3] POLAK E,RIBIERE G. Note Sur La Convergence De MéThodes De Directions ConjuguéEs[J].ESAIM:Mathematical Modelling and Numerical Analysis-Modélisation Mathématique et Analyse Numérique,1969,3(R1):35-43

[4] POLYAK B T. The Conjugate Gradient Method in Extremal Problems[J].USSR Computational Mathematics and Mathematical Physics,1969,9(4):94-112

[5] FLETCHER R.Practical Methods of Optimization Vol 1:Unconstrained Optimization[M].New York:John Wiley & Sons,1987

[6] LIU Y,STOREY C. Efficient Generalized Conjugate Gradient Algorithms,Part 1:Theory[J].Journal of Optimization Theory and Applications,1991,69(1):129-137

[7] DAI Y H,YUAN Y. A Nonlinear Conjugate Gradient Method with a Strong Global Convergence Property[J].SIAM Journal on Optimization,1999,10(1):177-182

[8] POWELL M J D. Ncoconvex Minimization Calcalations and the Conjugate Gradient Method[C]∥IN:lecture Notes in Mathematics. Berlin:Springer-verlag,1984

[9] HUANG H D,LI Y J,WEI Z X. Global Convergence of a Modified Prp Conjugate Gradient Method[J].Journal of Mathematical Research Exposition，2010,30(1):141-148

[10] 江羡珍，简金宝，马国栋.具有充分下降性的两个共轭梯度法[J].数学学报,2014,57(2):365-372

JIANG X Z,JIAN J B,MA G D.Two Conjugate Gradient Methods with Suffient Descent Property[J].Acta Mathematica Sinica,2014,57(2):365-372

[11] 黎小林.基于Wei-Yao-Liu共轭梯度参数的修正共轭梯度算法[D].重庆：重庆师范大学，2015

LI X L.Conjugate Gradient Algorithms Based on the Conjugate Gradient Parameter of Wei-Yao-Liu[D].Chongqing:Chongqing Normal University，2015

[12]DAI Y H,YUAN Y X. Nonlinear Conjugate Gradient Methods(in chinese)[M].Shanghai:Shanghai Scientific and Technical Publishers,2000

[13] 吴双江.带有最优参数选取的修正DL共轭梯度法[J].重庆工商大学学报(自然科学版),2015，32(8)：6-9

WU S J.The Modified DL Conjugate Gradient Method with Optimal Parameter Choices[J].Journal of Chongqing Technology and Business University (Naturnal Science Edition),2015，32(8)：6-9

责任编辑：李翠薇

An Improved NVPRP Method

WU Su-hua

(School of Mathematical Science, Chongqing Normal University, Chongqing 401331, China)

Nonlinear conjugate gradient method is one of the most effective methods to solve large-scale unconstrained problems. This paper presents a class of modified conjugate gradient algorithms. The new algorithm generalizes the conjugate gradient parameter algorithm of Huang Haidong et al, and has sufficient descent property without depending on any line search. Then, under Wolfe non-accurate line search, the global convergence of the new algorithm is obtained.

unconstrained optimization; conjugate gradient algorithm; sufficient descent property; global convergence

2016-03-12；

2016-04-06.

吴素花(1991-)，女，重庆秀山人，硕士研究生，从事最优化理论和算法研究．

10.16055/j.issn.1672-058X.2017.0002.007

O225

A

1672-058X(2017)02-0031-03