Bernstein Bezout矩阵与可控制型/可观测型矩阵之间的联系*

郑婷婷, 吴化璋

(安徽大学 数学科学学院，合肥 230039)

Bernstein Bezout矩阵与可控制型/可观测型矩阵之间的联系*

郑婷婷, 吴化璋**

(安徽大学 数学科学学院，合肥 230039)

通过多项式标准幂基与Bernstein基之间的转换关系给出了经典Bezout矩阵与Bernstein Bezout矩阵之间的相互联系；同时,由标准线性控制系统中的可控制型/可观测型矩阵构造出Bernstein基下的线性控制系统理论中的(广义)可控制型/可观测型矩阵,并建立Bernstein Bezout矩阵与对应的(广义)可控制型/可观测型矩阵之间的联系，所得结果和标准幂基下的有关结果是平行的.

标准幂基;Bernstein基;Bezout矩阵;Bernstein Bezout矩阵;可控制型/可观测型矩阵

0 引 言

用Rn[x]表示实数域R上次数不超过n-1的线性多项式空间,令

π(x)=(1,x,…,xn-1)T

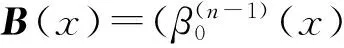
又设a(x)和b(x)分别是它们对应的关于标准幂基的表达式,即

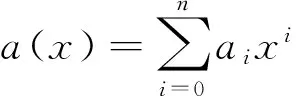
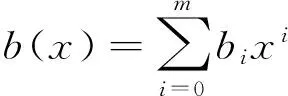
考察下面分别由a(x)与b(x)生成的关于标准幂基的双线性函数：

(1)

和f(x)与g(x)生成的关于Bernstein基的双线性函数：

(2)

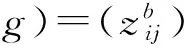
Bezout矩阵的研究有着悠久的历史,起初主要用来判断多项式的求根问题.近些年,由于它在多项式与线性控制系统理论、线性系统的实现理论、结构矩阵理论等领域有着广泛的应用[3-6],从而受到数学工作者和工程技术人员的重视.近些年来,Bezout矩阵被推广到一些多项式基下进行研究[7-12].

在线性控制系统理论中,Bezout矩阵可通过伴侣矩阵、可控制型/可观测型矩阵等来表示，而这些矩阵在判定一个线性系统是否可控制与是否可观测中起着非常重要的作用[3].此处主要讨论Bernstein基下的Bezout矩阵,并试图建立与线性控制系统中的(广义)可控制型/可观测型矩阵等之间的联系.得到的关系式可以看作是经典Bezout矩阵与可控制/可观测型矩阵之间关系的一个推广.

1 经典Bezout矩阵与可控制/可观测型矩阵

令Tn-1是标准幂基向量π(x)与Bernstein多项式基向量B(x)之间的转移矩阵,满足Tn-1B(x)=π(x).为了方便起见,下面用T来代替Tn-1,即

TB(x)=π(x)

矩阵T=(tij)及其逆矩阵T-1=(sij)可直接算出[2]. 由于f(x)=a(x),g(x)=b(x),根据以上Bezout矩阵的定义,有如下关系式成立：

TTB(a,b)T=B(b)(f,g)

(3)

如果g(x)≡b(x)=1,那么

B(b)(f,1)=TTB(a,1)T

(4)

再令S(a)=B(a,1)，S(b)(f)=B(b)(f,1),那么式(4)可简写为

S(b)(f)=TTS(a)T

(5)

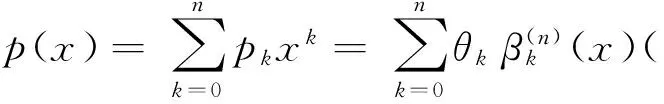
它的(关于Bernstein多项式基)广义伴侣矩阵记为

C(b)(p)=T-1C(p)T

(6)

众所周知,经典Bezout矩阵有如下的Barnett分解.

引理1[4]经典Bezout矩阵满足下列公式：

B(a,b)=S(a)b(C(a)T)

(7)

对于Bernstein Bezout矩阵B(b)(f,g)有如下形式的Barnett型分解公式.

引理2 Bernstein Bezout矩阵满足下面Barnett型分解公式：

B(b)(f,g)=S(b)(f)g(C(b)(f)T)

其中S(b)(f)=TTS(f)T-1.

证明 利用式(4)—(6)和引理2得到：

B(b)(f,g)=TTB(a,b)T=

TTS(a)b(C(a)T)T=

TTS(f)T-1Tg(C(f)T)T=

S(b)(f)g(C(b)(f)T)

在线性控制系统中,经典Bezout矩阵有着重要应用,通常可由可控制型/可观测型矩阵和它们的逆来表示.事实上,考虑下面可控制/可观测的单输入系统：

,y=MTw

(8)

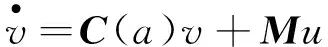
(9)

其中，

并且，

,…,anbn-1-an-1bn)T

其中ai和bj分别是a(x)和b(x)的系数.假设式(8)和式(9)分别是完全可观测的和完全可控制的系统,那么根据对偶性原则,它们的两个可控制型矩阵定义为

CI≡C(C(a)T,D)=(D,C(a)TD,…,(C(a)T)n-1D)

CII≡C(C(a),M)

(10)

两个可观测型矩阵定义为

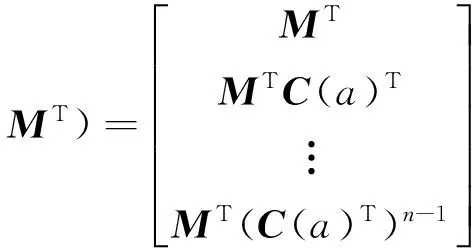
OII≡O(C(a),DT)

(11)

这两类矩阵满足下列关系式

(12)

另一方面，很容易推断等式(13)成立:

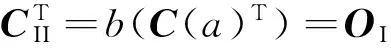
(13)

因此,根据引理2以及B(f,g)的对称性，很容易得到下列经典Bezout矩阵关于可控制性与可观测性矩阵的表示.

引理3[3]沿用上面记号，并设a(x)和b(x)互素.那么Bezout矩阵B(a,b)有如下表示:

B(a,b) = (CI)-1OI=CII(OII)-1=

(OII)-1OI=CII(CI)-1

(14)

2 Bernstein Bezout矩阵与可控制型/可观测型矩阵

本节将考虑Bernstein Bezout矩阵B(b)(f,g)的一个关于(广义)可控制型/可观测型矩阵类似表示.为此,考虑一般的可控制型/可观测型的单输入系统:

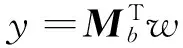
(15)

(16)

其中Db=TTDT,Mb=T-1MT.分别构造两个广义可控制型矩阵和广义可观测型矩阵如下：

CI(b)≡Cb(C(b)(f)T,Db)=

(Db,C(b)(f)TDb,…,(C(b)(f)T)n-1Db)

CII(b)≡Cb(C(b)(f),Mb)

(17)

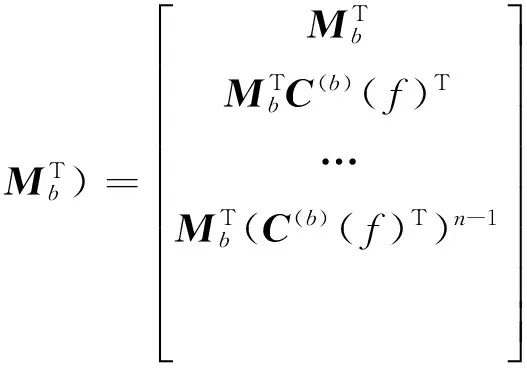
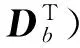
(18)

容易验证这两类矩阵之间存在以下关系:

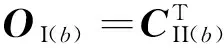
(19)

下面给出Bernstein Bezout矩阵B(b)(f,g)关于(广义)可控制型/可观测型矩阵(17)和(18)的表示定理.

定理1 沿用上面记号，并设f(x)和g(x)互素，那么Bernstein Bezout矩阵有如下的矩阵表示:

B(b)(f,g)=(CI(b))-1OI(b)=CII(b)(OII(b))-1=

(OII(b))-1OI(b)=CII(b)(CI(b))-1

(20)

证明 先证第一个等式.根据式(10)(11)和式(17),有

CI(b)=(Db,C(b)(f)TDb,…,(C(b)(f)T)n-1Db)=(TTDT,TTC(f)TT-tTTDT,…,TT(C(f)T)n-1T-tTTDT)=

TT(D,C(f)TD,…,(C(f)T)n-1D)T=TTCIT

(21)

又

(22)

式(21)、(22)结合,有

T-1B(f,g)T-T=B(b)(f,g)

因此,式(20)中的第一个等式得证.

剩下的可根据式(17)(18)(19)以及Bernstein Bezout矩阵的对称性得到.

从定理1证明过程和等式：

容易得到下面的公式.

推论1 设记号如前,则式(23)成立

(23)

注释:从推论1不难看出,定理1是Bernstein Bezout矩阵B(b)(f,g)的一种广义Barnett型分解公式.因为从定理1的第一个等式和推论1可得：

B(b)(f,g)=(CI(b))-1OI(b)=S(b)(f)g(C(b)(f)T)

(24)

式(24)与引理2完全一致.

[1] BARNETT S. Matrices in Control Theory[M].London:Van Nostrand-reinhold,1971

[2] BINI D A,GEMIGNANI L. Bernstein Bezoutian Matrices[J].Linear Algebra and Its Applications,2004(315):319-333

[3] BARNETT S.Polynomials and Linear Control System[M].NewYork:Marcel Dekker,1983

[4] HEINIG G,ROST K.Algebraic Methods for Toeplitz-like Matrices and Operators[M].Basel:Springer,1984

[5] LANCASTER P,TISMENETSKY M.The Theory of Matrices (2nd edition)[M].New York:Academic Press,1985

[6] BINI D,PAN V.Numerical and Algebraic Computations with Matrices and Polynomials[M].Boston:Birkhauser,1994

[7] GOVER J,BARNETT S.A Generalized Bezoutian Matrix[J].Linear and Multilinear Algebra,1990(27):33-48

[8] MANI J,HARTWIG R E.Generalized Polynomial Bases and the Bezoutian[J].Linear Algebra and Its Applications,1997(251):293-320

[9] YANG Z H,HU Y J.A Generalized Bezoutian Matrix with Respect to a Polynomial Sequence of Interpolatory Type[J].IEEE Transactions on Automatic Control,2004,49(10):1783-1789

[10] WU H Z.Generalized Polynomial Bezoutian with Respect to a Jacobson Chain Basis over an Arbitrary Field[J].Linear Algebra and Its Applications,2010(432):3351-3360

[11] WU H Z.Resultant Matrices and Bezoutians under the Polynomial Bases Generated by a Bilinear Transformation Function[J].Journal of Anhui University (Natural Science Edition),2015,39(6):1-8

[12] 吴梅.一类特殊的Bezout矩阵[J].重庆工商大学学报(自然科学版),2015,32(4):1-5

WU M.A Special Class of Bezout Matrix[J].Journal of Chongqing Technology and Business University (Natural Science Edition),2015,32(4):1-5

[13] WOLTERS H J,FARIN G E.Geometric Curve Approxi-Mation[J].Comput Aided Geom Design,1997,14(6): 499-513

[14] WINKER J R.A Companion Matrix Resultant for Bernstein Polynomials[J].Linear Algebra and Its Applications,2003(362):153-175

[15] WINKER J R.The Transformation of the Companion Matrix Resultant between the Power and Bernstein Polynomial Bases[J].Applied Numerical Mathematics,2004(48):113-126

责任编辑：罗姗姗

Connections between Bernstein Bezout Matrix and Generalized Controllability/Observability-type Matrices

ZHENG Ting-ting, WU Hua-zhang

(School of Mathematical Sciences, Anhui University, Hefei 230039, China)

The relationships between the classical Bezout matrix and Bernstein Bezout matrix are given by the transformation matrix of the standard power basis and Bernstein polynomial basis. Meanwhile, a generalized linear control system for the Bernstein polynomial basis is established from the classical one, and a kind of generalized controllability/observability-type matrices is constructed correspondingly. Finally, connections between Bernstein Bezout matrix and generalized controllability/observability-type matrices are discussed. The results obtained are parallel to the previous ones for the standard power basis.

standard power basis; Bernstein basis; Bezout matrix; Bernstein Bezout matrix; controllability/observability-type matrix

2016-06-07;

2016-07-05.

安徽省自然科学基金(1208085MA02)；安徽大学大学生科研训练项目(A01414110).

郑婷婷(1997-),女,陕西西安人,从事应用数学研究.

**通讯作者：吴化璋 (1966-),男,安徽全椒人,教授,博士,从事矩阵与算子理论研究. E-mail:wuhz@ahu.edu.cn.

10.16055/j.issn.1672-058X.2017.0002.003

O151

A

1672-058X(2017)02-0012-04