迭代算法求解矩阵方程埃尔米特双对称解*
2017-03-27胡志增杨春花
胡志增, 杨春花
(湘潭大学 数学与计算科学学院,湖南 湘潭 411105)
迭代算法求解矩阵方程埃尔米特双对称解*
胡志增, 杨春花
(湘潭大学 数学与计算科学学院,湖南 湘潭 411105)
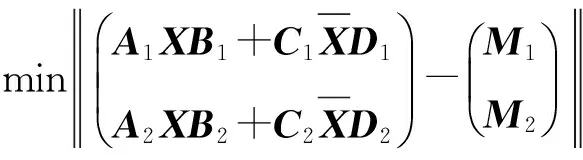
复矩阵方程;迭代算法;埃尔米特双对称解
1 问题论述
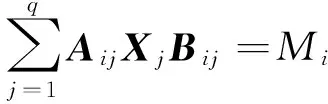
本文主要考虑以下问题.
问题Ⅰ 已知矩阵A1,A2,C1,C2∈Cp×n,B1,B2,D1,D2∈Cn×q,M1,M2∈Cp×q,求矩阵X∈HBSCn×n使得
(1)
2 问题Ⅰ的规范方程
以下主要给出式(1)的最小F范数剩余问题规范方程.
首先,给出推导过程中所用到的一些定义和引理.
定义1 设S⊆Cn×n,对于任意矩阵x1,x2∈S,以及任意数α∈(0,1),若都有αx1+(1-α)x2∈S,则称矩阵集S是凸的,用Qc表示Cn×n上的凸子集.
定义2 若对于任意x1,x2∈Qc以及α∈(0,1),矩阵函数f均满足f(αx1+(1-α)x2)≤αf(x1)+(1-α)f(x2),则称f:Qc→C是凸的.
定义3 若f:Qc→C连续且可微,则f的梯度定义为
引理1 若f:Qc→C是连续且可微的,则f在Qc是凸的当且仅当f(y)≥f(x)+〈▽f(x),y-x〉,对于所有x,y∈Qc.
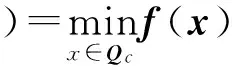
因为HBSCn×n是一个无界的、开的凸集,由式(1),定义HBSCn×n上的矩阵函数:
(2)
则函数F(X)是连续的、可微的,在HBSCn×n上也是凸的,所以由引理1、引理2,可得出以下引理.
引理3 设F(X)的定义式为式(2),则存在X*∈HBSCn×n满足
当且仅当▽F(X*)=0
引理4 矩阵X∈HBSCn×n当且仅当X=XH=SnXSn.
引理5 假设矩阵X∈HBSCn×n,则X+SnXSn∈HBSCn×n.
引理6 设矩阵A∈Cn×n,X∈HBSCn×n,则有
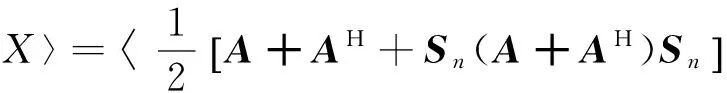
由F范数的基本性质以及矩阵内积,可知:
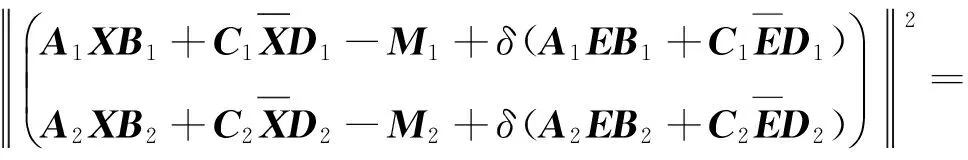


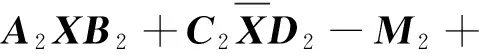
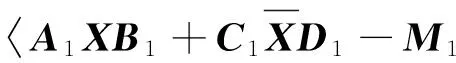


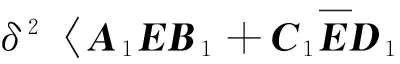
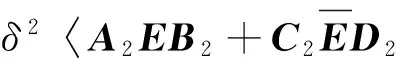

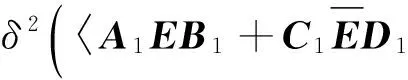
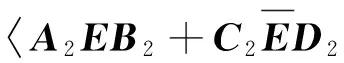
(3)
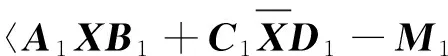
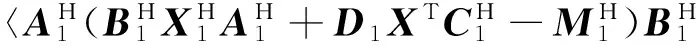
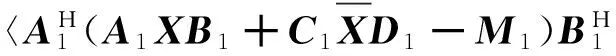
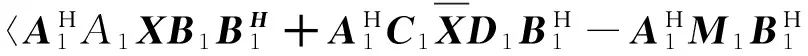
(4)
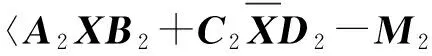
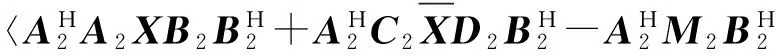
(5)
又对任意
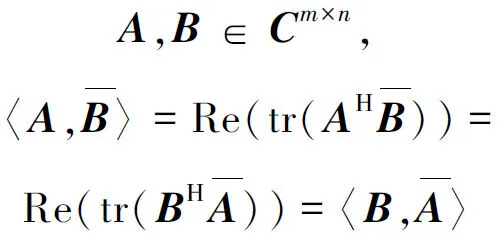
所以

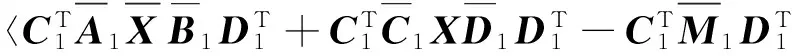
(6)
同理
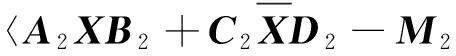
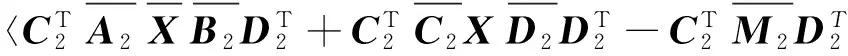
(7)
由式(4),式(6)以及引理6知

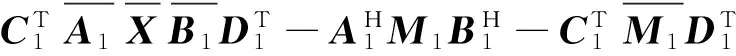
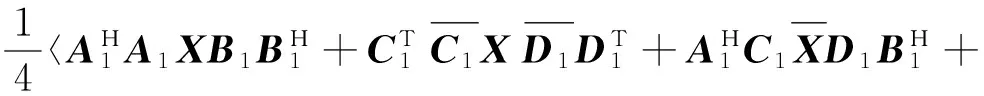
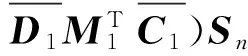
(8)
同理
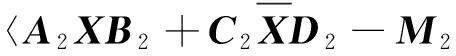
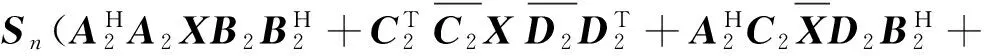
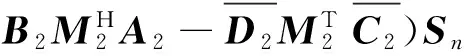
(9)
由泰勒级数展开式,知道
F(X+δE)=F(X)+δ〈▽F(X),E〉+∘(δ)∀X,
E∈HBSCn×n,δ∈R
(10)
代入式(8)、式(9)到式(3),然后对比式(10)可得到▽F(X).
由引理3可得到以下定理.
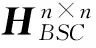
(11)
式(11)称为问题I的规范方程.
3 问题I的迭代算法
算法1
第1步:输入矩阵A1,A2,C1,C2∈Cp×n,B1,B2,D1,D2∈Cn×q,M1,M2∈Cp×q,以及任意初始矩阵X0∈HBSCn×n.
第2步:计算
R0=V-U(X0),P0=R0,k:=0
第3步: 如果Rk=0,则停止算法,否则令k:=k+1.
第4步:计算
第5步:回到第3步.
注1 因为X0以及U(X)属于HBSCn×n,所以可知由算法1得到的矩阵序列{Xk},{Rk}和{Pk}均是埃尔米特双对称矩阵,其中Rk是规范方程式(11)的剩余.
为了证明算法1的收敛性,先验证以下一些基本性质.
引理7 由算法1得到的矩阵序列{Ri}和{Pi},如果存在正整数k满足对所有的i=0,1,2,…,k有Ri≠0,则有:
(i) 〈Ri,Rj〉=0,〈Pi,U(Pj)〉=0,(i,j=0,1,2,…,k,i≠j);
(ii) 〈Ri,Pj〉=〈Rj,Pj〉,(0≤i≤j≤k).
证明 (i) 对任意矩阵X1,X2∈HBSCn×n,由引理6以及本文所用到的内积,容易验证〈X1,U(X2)〉=〈U(X1),X2〉,又因为〈A,B〉=〈B,A〉对所有A,B∈Cm×n均成立,所以对于(i)中的性质只需证明对所有的0≤i 当k=1时,〈R0,R1〉=〈R0,R0-t0U(P0)〉= 〈P0,U(P1)〉=〈U(P0),P1〉= 假定当0≤s 当s 〈Rs,Rj〉-〈Rs,tjU(Pj)〉=-tj〈Rs,U(Pj)〉= -tj〈U(Rs),Pj〉=-tj〈U(Ps+Ls-1Ps-1),Pj〉= -tj[〈U(Ps),Pj〉+Ls-1〈U(Ps-1),Pj〉]=0 〈Ps,U(Pj+1)〉=〈U(Ps),Pj+1〉= 〈U(Ps),Rj+1-LjPj〉= 当s=j时〈Rs,Rs+1〉=〈Rs,Rs-tsU(Ps)〉= 〈Rs,Rs〉-〈Rs,tsU(Ps)〉= 〈Rs,Rs〉-ts〈Rs,U(Ps)〉= 〈Ps,U(Ps+1)〉=〈U(Ps),Ps+1〉= 所以由归纳法证明了性质(i)的成立. (ii) 证明 由算法1以及引理7可知 Ri=Ri+1+tiU(Pi)=Ri+2+ti+1U(Pi+1)+tiU(Pi)= …=Rj+tj-1U(Pj-1)+…+tiU(Pi) 所以〈Ri,Pj〉=〈Rj,Pj〉+tj-1〈U(Pj-1),Pj〉+…+ ti〈U(Pi),Pj〉=〈Rj,Pj〉 (0≤i≤j≤k) 注2 因为算法1中得到的矩阵序列{Ri}是彼此正交的,而在有限维矩阵空间HBSCn×n中基一定是有限的,所以总存在正整数r使得Rr=0,所以该迭代算法一定会在有限步内停止,从而得到迭代解. 例 对于问题I给定矩阵A1,A2,B1,B2,C1,C2,D1,D2,M1,M2如下: 取初始矩阵X0=0∈HBSC5×5,应用算法1经过14步迭代,得到方程组的迭代解. [1] HUANG N,MA C.The Modified Conjugate Gradient Methods for Solving a Class of Generalized Coupled Sylvester-Transpose Matrix Equations[J].Computers and Mathematics with Applications,2014,67(8): 1545-1558 [2] LIU A,CHEN G,ZHANG X.A New Method for the Bisymmetric Minimum Norm Solution of the Consistent Matrix Equations[J].Journal of Applied Mathematics,2013(3) [3] DUAN X,LI C.A New Iterative Algorithm for Solving a Class of Matrix Nearness Problem[J].ISRN Computational Mathematics,2012 [4] LIN Y,WANG Q W.Generalized Reflexive and Generalized Antireflexive Solutions to a System of Matrix Equations[J].Journal of Applied Mathematics,2014(3):1-9 [5] CHEN D Q,YIN F,HUANG G X.An Iterative Algorithm for the Generalized Reflexive Solution of the Matrix EquationsAXB=E,CXD=F[J].Journal of Applied Mathematics,2012(9):701-708 [6] Zhou Z,Huang G.An Iterative Algorithm for the Reflexive Solution of the General Coupled Matrix Equations[J].The Scientific World Journal,2013(1) [7] XIE Y J,MA C F.The Matrix Iterative Methods for Solving a Class of Generalized Coupled Sylvester-Conjugate Linear Matrix Equations[J].Applied Mathematical Modelling,2015,39(16):4895-4908 [8] LIANG K,LIU J.Iterative Algorithms for the Minimum-Norm Solution and the Least-Squares Solution of the Linear Matrix Equations[J].Applied Mathematics and Computation,2011,218(7):3166-3175 [9] CAI J,CHEN G.An Iterative Algorithm for the Least Squares Bisymmetric Solutions of the Matrix EquationsA1XB1=C1,A2XB2=C2[J].Mathematical and Computer Modelling,2009,50(7):1237-1244 [10] 周金华,刘建州.矩阵方程ATXB-BTXTA=D的最小二乘解[J].重庆工商大学学报(自然科学版),2003(2):19-21 ZHOU J H,LIU J Z.The Least-square Solution of Matrix EquationATXB-BTXTA=D[J].Journal of Chongqing Technology and Business University (Natural Science Edition),2003(2):19-21 责任编辑:罗姗姗 An Iterative Algorithm for the Hermite Bisymmetric Solution to A Class of Complex Matrix Equations HU Zhi-zeng, YANG Chun-hua (School of Mathematics and Computational Science, Xiangtan University, Hunan Xiangtan 411105, China) complex matrix equations; iterative algorithm; Hermite bisymmetric solution 2016-09-14; 2016-10-23. 湖南省自然科学基金项目(2015JT2134). 胡志增(1991-),男,河南安阳人,硕士研究生,从事最优控制理论与计算研究. 10.16055/j.issn.1672-058X.2017.0002.002 O151.24 A 1672-058X(2017)02-0006-06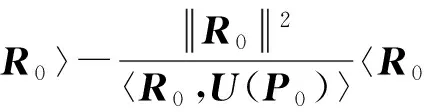

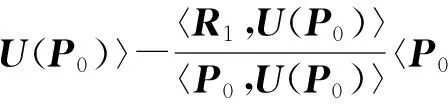
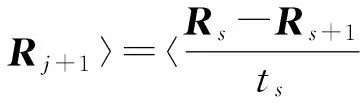
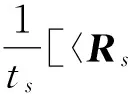
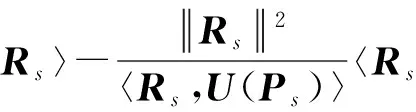
4 数值试验
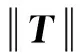




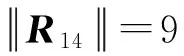
5 结束语

