柔性线缆连接的分离式卫星动力学建模
2017-03-27庞岩,李静,刘磊
庞 岩,李 静,刘 磊
(1.大连理工大学航空航天学院,大连116024;2.工业装备结构分析国家重点实验室,大连116024; 3.西北工业大学航天学院,西安710072)
柔性线缆连接的分离式卫星动力学建模
庞 岩1,2,李 静1,刘 磊3
(1.大连理工大学航空航天学院,大连116024;2.工业装备结构分析国家重点实验室,大连116024; 3.西北工业大学航天学院,西安710072)
基于拉格朗日法建立柔性线缆连接的分离式磁耦合卫星刚柔耦合动力学模型,并基于该模型研究柔性线缆对分离式卫星隔振性能以及指向性能的影响。仿真结果表明,柔性线缆将明显降低分离式卫星对服务模块低频扰动的隔振性能,由于柔性线缆的存在,低频扰动将使载荷模块稳态时的姿态精度和稳定度大幅下降。柔性线缆也会影响载荷模块的指向控制精度,采用相同的PD控制器,有柔性线缆时载荷模块指向稳态误差大于无柔性线缆时载荷模块指向稳态误差4个数量级。柔性线缆对载荷模块性能影响明显,所建动力学模型对提高分离式卫星建模和控制精度有重要意义。
分离式卫星;柔性线缆;拉格朗日法;刚柔耦合动力学
0 引 言
超静力学环境是敏感载荷的迫切要求,本文研究一种特殊设计的超静卫星构型,即分离式卫星的动力学建模。分离式卫星是洛克希德·马丁公司提出来的一种新型超静卫星构型,其由载荷模块、服务模块以及两个模块之间的磁耦合界面组成。载荷模块上安装有需要高精度以及高稳定度控制的敏感设备,比如高分辨率望远镜等。服务模块安装有反作用飞轮、推进器、挠性太阳帆板等有扰设备,因此卫星微振动源主要集中在服务模块。理想磁耦合界面由非接触作动器(如音圈作动器)、非接触传感器以及无线能量和信息传递通道组成,以保证载荷模块超静性能。由于载荷模块和服务模块之间无机械连接,这种结构理论上可以实现零刚度完全隔振,并且可以通过磁耦合作动器对载荷模块进行姿态和位置操作[1-5]。文献[2]以NGST空间望远镜的构型为例通过数值仿真比较了分离式卫星和传统扰动源隔振卫星的隔振性能,结果表明分离式卫星较传统卫星其隔振性能提高两个数量级,证实了分离式卫星构型对微振动隔离的有效性。文献[4]研究了分离式卫星构型在敏捷卫星中的应用,其数值仿真和地面实验结果表明分离式卫星构型在满足隔振性能的同时能够实现对载荷模块的快速指向控制。
理想分离式卫星其载荷模块和服务模块之间完全没有物理连接,但实际中由于现有技术的局限,载荷模块和服务模块之间的能量传递需要柔性线缆连接[2,5]。文献[2]中仿真结果表明载荷模块和服务模块之间存在柔性线缆耦合时,其低频段隔振性能较完全非接触情况下降十倍以上,说明柔性线缆严重影响了分离式卫星的隔振性能,但文中并未给出柔性线缆连接的分离式卫星动力学模型。许域菲建立了无机械连接时,对载荷进行六自由度操作的一种动力学模型,但还没有研究有线缆连接时的情况[6]。
柔性线缆连接的分离式卫星不同于绳系卫星。绳系卫星系绳两端的模块分别采用常规执行机构进行姿态和轨道控制,而本文研究的分离式卫星,其载荷模块的姿态、位置(轨道)通过载荷模块和服务模块之间的磁耦合作动器进行控制。对绳系卫星的动力学建模已经有了大量的研究[7-12],但这些动力学模型尤其是在闭环控制时并不适合本文研究的分离式卫星。
本文以柔性线缆连接的分离式卫星为研究对象,基于拉格朗日法构建其刚柔耦合动力学模型并进行仿真研究。拉格朗日法从能量角度出发,无需计算系统内约束力,推导过程简洁,适用于多自由度复杂系统建模,因而被广泛的应用在机器人动力学以及多体系统动力学等领域中[13-17]。针对所建动力学模型,本文仿真分析了柔性线缆连接对分离式卫星的隔振性能以及载荷模块控制的影响程度。
1 系统描述以及拉格朗日法简述
1.1 柔性线缆连接的分离式卫星系统描述
柔性线缆连接的分离式卫星基本结构如图1所示。图中载荷模块的姿态和位置通过非接触作动器控制,作动器的数量以及安装构型可以有多种形式,比如具有六个作动器的hexapod构型[1,5]。为使作图简洁,本文在图1中只给出了某一个作动器及其传感器示意图,记其编号为i。本文假设载荷模块和服务模块均为刚体,且载荷模块和服务模块之间的柔性线缆可视为一个具有一定刚度和阻尼的弹簧/阻尼元件[18]。
为利用拉格朗日法建模,将图1所示系统写为图2所示的向量形式,并建立用于描述系统运动的坐标系。
图2中,L-XYZ是卫星的轨道坐标系,L是整个系统的质心;S-XYZ和P-XYZ分别表示服务模块和载荷模块的体坐标系,S和P分别是服务模块和载荷模块的质心;SE-XYZ以及PE-XYZ分别是服务模块和载荷模块在标称位置时的体坐标系;rSE和rPE分别表示服务模块和载荷模块处于标称位置时质心在轨道坐标系下的位置矢量;ΔrS和ΔrP分别为载荷模块和服务模块的质心偏离标称位置的矢量;du和pu表示服务模块和载荷模块的柔性线缆连接点在各自体坐标系下的位置矢量,K和C是柔性线缆简化模型在轨道坐标系下的刚度阵和阻尼阵;di和pi表示载荷模块和服务模块的第i个作动器连接点在各自体坐标系下的位置矢量。
图2中载荷模块和服务模块的运动可分解为跟随轨道坐标系的轨道运动以及偏离标称位置的受扰运动两部分[18]。本文在推导分离式卫星动力学方程时忽略整星轨道运动,把轨道坐标系近似看成一个惯性系,且假设SE-XYZ、PE-XYZ、L-XYZ三个坐标系互相平行。
1.2 拉格朗日法简述
适用于完整系统的第二类拉格朗日方程如下所示:
式中:L=T-V是拉格朗日函数,T为系统的总动能,V为系统的总势能;qk是系统的第k个广义坐标,f是系统的自由度;F为瑞利耗散函数,Qk表示和广义坐标对应的广义力。
求取广义力通常采用式(2)所示虚功原理[19]
式中:W为系统主动力虚功。
利用拉格朗日法建模时,需要选取合适的广义坐标来描述系统的运动,图2所示系统有两个刚体,要完整描述系统运动需要12个广义坐标。本文选择描述载荷模块运动的广义坐标为 qP= (xp,yp,zp,θpx,θpy,θpz)T,式中:xp、yp、zp表示矢量ΔrP在轨道坐标系下投影的三个分量,用来描述刚体平动,θpx、θpy、θpz表示载荷模块体坐标系P-XYZ绕X-Y-Z三轴相继转动后和PE-XYZ平行所需要的转动欧拉角,用来描述刚体转动。同样,对于服务模块选择广义坐标为qS=(xs,ys,zs,θsx,θsy,θsz)T,其中各分量和载荷模块广义坐标中各分量定义对应。第2节将给出有柔性线缆连接的分离式卫星动力学模型的详细推导过程。
2 柔性线缆连接的分离式卫星动力学建模
首先求系统动能表达式。图2所示系统动能包括载荷模块和服务模块的平动动能以及转动动能,其具体表达式如下
式中:mp、ms分别为载荷模块和服务模块质量,IP、IS分别为载荷模块和服务模块在各自体坐标系下的转动惯量,ωP、ωS分别表示载荷模块和服务模块的体坐标系相对轨道坐标系的转动角速度矢量。
为简化推导,本文假设IP、IS为对角阵,记IP=diag(Ipx,Ipy,Ipz),IS=diag(Isx,Isy,Isz)。为书写简便记sinθ=Sθ,cosθ=Cθ。则式(3)可写为如下矩阵形式。
式中:
式中:
将式(5)中各广义坐标分量下标 p换成 s可得MS(qS)表达式。
下面求势能表达式。本文不考虑系统轨道运动,系统的势能只有柔性线缆的弹性势能,在标称位置时柔性线缆伸长量为0[18]。记柔性线缆的长度变化矢量为Δu,则柔性线缆的弹性势能为
式中:
若pu在载荷模块体坐标系下的分量为pu= (pu1,pu2,pu2)T,du在服务模块体坐标系下的分量为du=(du1,du2,du2)T。将式(8)代入式(7)中可得ΔuP的具体表达式为
将式(9)中广义坐标各分量下标p换成s,并用du各分量替换 pu各分量即可得 ΔuS的表达式。再将ΔuP和ΔuS的表达式代入式(6)即可得势能表达式。
接下来求系统的瑞利耗散函数。本文选择的瑞利耗散函数具有如下形式
对式(9)求导可得
式中:
式中:
同理可得
将式(13)中各广义坐标分量下标p替换成s,并将pu各分量替换成du各分量可得到Rdu(qS)表达式。因此系统的瑞利耗散函数为
将式(4)、(6)、(14)代入式(1)即可得分离式卫星动力学方程,写成矩阵形式如下
式(15)中上半部分是载荷模块的动力学方程,下半部分是服务模块的动力学方程,QP和QS分别为与广义坐标向量 qP以及 qS对应的广义力。
以载荷模块为例,将式(15)中载荷模块动力学方程展开可得
式(16)中右端各项表达式如下
式中:
式中:
根据式(11)可得
因此有
同理对于服务模块有
将CP1、CP2表达式中各广义坐标下标由p换为s可得CS1、CS2表达式。
接下来求式(15)中广义力QP和QS的具体表达式。图2中第i个作动器在轨道坐标系下的支杆矢量为
支腿的速度矢量为
作动器沿支腿方向的伸长速度为
记第i个作动器的作用力大小为,假设每个作动器的作用力方向沿支腿伸长方向,记f=(f1,f2,…)T,那么根据虚功原理有
根据式(26)可得
之后,将式(20)~(21)、(27)~(28)代入式(15)即可得分离式卫星在轨道坐标系下的动力学方程。若载荷模块以及服务模块的运动是在标称位置附近的小角度运动,那么忽略高阶小量,可得近似线性后的如下动力学方程
上式中E3×3表示3阶单位矩阵,分别表示矢量pu、bu的反对称矩阵,JP、JS此时为常矩阵。
3 分离式卫星载荷模块仿真分析
本文以载荷模块为研究对象,分析柔性线缆连接对载荷模块在开环状态下的指向性能以及闭环指向控制精度的影响。
3.1 载荷模块开环响应分析
将服务模块的六自由度广义坐标看作载荷模块的输入端扰动,利用近似线性化之后的载荷模块动力学方程,即式(29)可以求得服务模块广义坐标qP到载荷模块广义坐标qS的传递函数。载荷模块动力学方程是一个六输入—六输出系统,若采用Bode图描述输入输出关系共需要36个Bode图,过于繁琐,于是本文采用奇异值曲线来描述输入输出关系[21]。载荷模块动力学方程的基本参数如表 1所示。
服务模块广义坐标到载荷模块广义坐标的传递函数奇异值曲线如图3所示
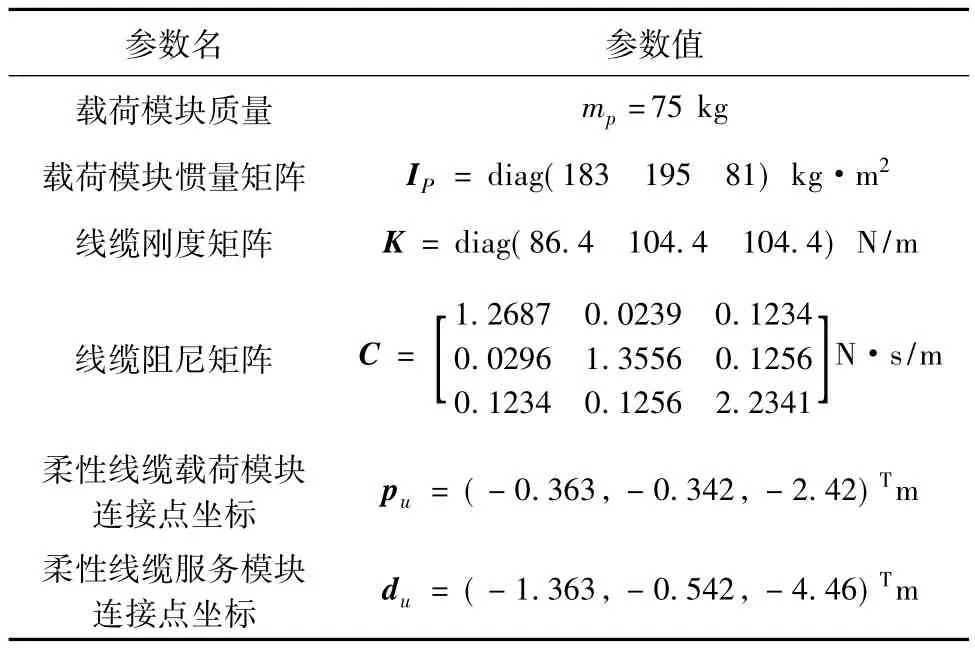
表1 载荷模块基本参数Table 1 Argument of payload module
从图3的奇异值曲线可以看出,在0.01 Hz~1 Hz频段内,来自服务模块的扰动传递到载荷模块时在某些方向上会引发谐振,且谐振峰值超过30 dB。而对于频率高于1 Hz的扰动,载荷模块的响应表现出幅值衰减的特性,且频率越高,衰减效果越强。因此,在有柔性线缆连接的情况下,服务模块对载荷模块的影响主要是在低频段。分析部分低频段发生耦合振动的原因,可以看出,有柔性线缆连接时,通常线缆刚度较低且阻尼小,柔性线缆与载荷模块连接的基频低,因此开环状态下柔性线缆对载荷模块发生低频耦合振动。柔性线缆很大程度上衰减了高频干扰但是在低频段会产生谐振,谐振频率和峰值取决于柔性线缆的刚度和阻尼。服务模块对载荷模块的耦合影响也主要在低频段。
下面以载荷模块广义坐标的第四个分量θpx为例,仿真其对服务模块输入θsx的时域响应。仿真时采用载荷模块完整的非线性动力学模型,取θsx为幅值0.0001°、频率0.4 Hz以及幅值0.00001°、频率20 Hz的两个信号的叠加。载荷模块的姿态角和姿态角速度响应如图4和图5所示,图5中ωsx=sx,ωpx=px。为说明柔性线缆的影响,图4和图5中给出了无线缆连接时载荷模块的响应作为对比。
从图4和图5中结果可以看出,在没有柔性线缆连接时,服务模块的扰动对载荷模块几乎没有影响,载荷模块的姿态精度优于1×10-8(°),姿态稳定度优于1×10-8(°/s)。而有柔性线缆连接时,载荷模块姿态精度下降到8×10-4(°),姿态稳定度下降到2×10-3(°/s)。可见,柔性线缆连接会严重影响载荷模块在稳态时的指向性能,图4和图5中结果也可看出影响载荷模块姿态精度和姿态稳定度的主要因素是θsx中频率为0.4 Hz的低频分量,而服务模块的高频分量对载荷模块没有太大影响,时域仿真结果和线性化模型的频域结果一致。
3.2 载荷模块闭环响应分析
本节分析柔性线缆连接对载荷模块指向控制的影响,作为对比分别仿真在没有柔性线缆连接和有柔性线缆连接时载荷模块的指向控制。仿真时不考虑作动器的具体构型,把式(29)中JTPf单纯等效为载荷模块的主动控制力和力矩,并采用如下所示的PD控制器
式中:,r为各广义坐标的参考输入,本文取 ωn=0.4π,ξ=0.707。取 r= (0.04 m 0.05 m 0.06 m 4°5°6°)T,载荷模块基本参数同3.1节中一致,对载荷模块六自由度控制的仿真结果如下
从图6~11中仿真结果可以看出,没有柔性线缆连接时,在PD控制器作用下载荷模块12 s内可以收敛到稳态值,且各方向控制的稳态误差小,控制精度高。有柔性线缆连接时,在同样的PD控制器作用下载荷模块在12 s内能收敛到稳态值,但是稳态误差明显增大。有线缆连接和无线缆连接两种情况下的PD控制稳态误差结果如表2所示,从表中结果可以看出,有线缆连接时载荷模块稳态误差高于无线缆连接时稳态误差4个数量级,说明柔性线缆连接会严重影响载荷模块六自由度的指向控制精度。

表2 载荷模块主动控制的稳态误差Table 2 Steady-state error of payload module in active control
4 结 论
本文基于拉格朗日法建立了柔性线缆连接的分离式卫星的动力学模型,并研究了柔性线缆对载荷模块的隔振性能以及指向控制的影响。开环频域和时域仿真结果表明,根据线缆参数和平台参数的不同,柔性线缆主要影响分离式卫星在低频段的隔振性能。闭环指向控制仿真结果表明在同样的PD控制器作用下,有无线缆稳态误差相差4个数量级。仿真结果证实柔性线缆对分离式卫星性能影响明显,论文建议下一步工作对其柔性线缆动力学进行补偿,以提高分离式卫星性能。
[1] Pedreiro N,Carrier A C,Lorell K R,et al.Disturbance-free payload concept demonstration[C].AIAA Guidance,Navigation,and Control Conference and Exhibit,Monterey,California,USA,August 5-8,2002.
[2] Pedreiro N.Spacecraft architecture for disturbance-free payload[J].Journal of guidance,Control,and Dynamics,2003,26 (5):794-804.
[3] Gonzales M A,Pedreiro N,Roth D E,et al.Unprecedented vibration isolation demonstration using the disturbance-freepayload concept[C].AIAA Guidance,Navigation,and Control Conference and Exhibit,Providence,Rhode Island,August 16-19,2005.
[4] Pedreiro N,Park M.Compiler:US,770252[P]2002-08-08.
[5] Pedreiro N,Gonzales A G,Foster B W,et al.Disturbance-free payload[C].AIAA Guidance, Navigation, and Control Conference and Exhibit,San Francisco,California,USA,August 15-18,2005.
[6] Xu Y F,Liao H,Liu L,et al.Modeling and robust H-infinite control of a novel non-contact ultra-quiet stewart spacecraft[J].Acta Astronautica,2015,107:274-289.
[7] HuangJ,MaG F,Liu G.Nonlineardynamicsand reconfiguration control of two-satellite coulomb tether formation at libration points[J].Aerospace Science and Technology,2014,39:501-512.
[8] 王长青,张马林,李爱军,等.空间系绳系统的动力学建模与轨迹跟踪控制[J].应用力学学报,2014,31(6):896-899.[Wang Chang-qing,Zhang Ma-lin,Li Ai-jun,et al.Dynamic stability of a high pier under the transverse impact considering geometrical nonlinearity[J].Chinese JournalofApplied Mechanics,2014,31(6):896-899.]
[9] 余本嵩,文浩,金栋平.绳系卫星编队动力学及控制研究进展[J].动力学与控制学报,2015,13(5):321-328.[Yu Bensong,Wen Hao,Jin Dong-ping.Advances in dynamics and control of tethered satellite formations[J].Journal of Dynamics and Control,2015,13(5):321-328.]
[10] Pang Z J,Yu B S.Chaotic motion analysis of a rigid spacecraft dragging a satellite by an elastic tether[J].Acta Mech,2015,226(8):2761-2771.
[11] 胡仄虹,黄攀峰,孟中杰.空间绳系机器人系统动力学建模与仿真研究[J].宇航学报,2014,35(1):28-38.[Hu Ze-hong,HuangPan-feng,MengZhong-jie.Dynamics modelingand simulation of tethered space robot system[J].Journal of Astronautics,2014,35(1):28-38.]
[12] 张健,王峰,孙兆伟.电动力绳系卫星轨道机动策略研究[J].宇航学报,2014,35(10):1182-1188.[Zhang Jian,Wang Feng,Sun Zhao-wei.Research on orbit maneuver strategy for electrodynamic tether satellite[J].Journal of Astronautics,2014,35(10):1182-1188.]
[13] Min B C,Hong J H,Matson E T.Adaptive robust control (ARC)for an altitude control of a quadrotor type UAV carrying an unknown payloads[J].ICCA,2011,1416(4):1147- 1151.
[14] Eftekhari M,Eftekhari M,Karimpour H.Neuro-fuzzy adaptive control of a revolute stewart platform carrying payloads of unknown inertia[J].Robotica,2015,33(9):2001-2024.
[15] Mahir A,Deng S P,Qi Y M.Gantry robot dynamic analysis based on Lagrange’s motion equation[J].Key Engineering Materials,2016,693:1741-1746.
[16] Zhang J,Zhang J,Wang C.Dynamic analysis and simulation on bionics quadruped robot[J].The Open Automation and Control Systems Journal,2015,7(1):1088-1093.
[17] Lyu J T,Gao D.Attitude synchronization for multiple spacecraft with input constraints[J].Chinese Journal of Aeronautics,2014,27(2):321-327.
[18] Johnson T L,Tolson R H.Development of a simulation capability for the space staion Active Rack Isolation[R].Hampton,Virginia:Langley Research Center,March 1998.
[19] Ahmed A H.Active isolation and damping of vibrations via Stewart platform[D].Brussels:Universite Libre de Bruxelles,2003.
[20] Hajimirzaalian H,Moosavi H,Massah M.Dynamics analysis and simulation of parallel robot Stewart platform[C].The 2nd International Conference on Computer and Automation Engineering(ICCAE),Singapore,February 26-28,2010.
[21] 刘磊,王萍萍,孔宪仁,等.Stewart平台动力学建模及鲁棒主动隔振控制[J].宇航学报,2011,32(6):1231-1238.[Liu Lei,Wang Ping-ping,Kong Xian-ren,et al.Dynamic modeling and robust active isolation control of Stewart platform[J].Journal of Astronautics,2011,32(6):1231-1238.]
通信地址:辽宁省大连市大连理工大学航空航天学院(116024)电话:(0411)84706692
E-mail:ypang@dlut.edu.cn
作者简介:
刘 磊(1981-),男,副教授,主要从事空间微振动、微动力学与控制等研究。本文通信作者。
通信地址:陕西省西安市碑林区友谊西路西北工业大学航天学院(710072)
电话:(029)88492781
E-mail:Leiliu@nwpu.edu.cn
(编辑:张宇平)
Dynamics Modeling of the Separated Satellite with Flexible Cable
PANG Yan1,2,LI Jing1,LIU Lei3
(1.School of Aeronautics and Astronautics,Dalian University of Technology,Dalian 116024,China; 2.State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian 116024 China; 3.School of Astronautics,Northwestern Polytechnical University,Xi’an 710072,China)
The rigid-flexible coupling dynamics model of a separated satellite with flexible cable is derived using Lagrange method.Based on the proposed model,the flexible cable effect on the vibration isolation performance and pointing control of the satellite is investigated.The simulation result indicates that the flexible cable decreases the vibration isolation performance at low frequencies.Furthermore,the low frequency disturbances from the support module dramatically degrade the attitude accuracy and stability of the satellite.The flexible cable also has significant effect on the pointing control performance of the payload module.Using the same PD controller,the steady-state error of the payload module with flexible cable is 4 orders of magnitude larger than that of the payload module without flexible cable.It can be concluded that the performance of the payload module is seriously degraded by the flexible cable.The dynamics model in this paper is important on how to improve the modeling and control accuracy of the separated satellites.
Separated satellite;Flexible cable;Lagrange method;Rigid-flexible coupling dynamics
V412.4
A
1000-1328(2017)01-0001-09
10.3873/j.issn.1000-1328.2017.01.001
庞 岩(1977-),女,副教授,主要从事飞行器动力学建模、控制与仿真。
2016-08-10;
2016-11-23
国家自然科学基金(11402044,51675430,11302132);可靠性与环境工程技术重点实验室开放基金(KHZS20143003);中央高校基本科研业务费(DUT16QY23)
