立体几何教学中应培养学生的若干基本教学思想

陈志坚

数学思想方法是数学的灵魂。近几年的立体几何高考试题，在坚持考查“三基”和“四个能力”的同时，还把数学基本思想方法作为一个重要内容进行考查。立体几何常用的数学思想有化归思想、分类思想、基本量思想、函数与方程思想、数形结合思想、整体思想、类比与转换思想等，教学中应着重培养这些数学基本思想，特别是在基本概念、定理公式及例题示范中，一定要讲思想、讲方法。

一、化归思想

化归思想是立几中最重要的思想，它的一个具体体现是立体几何问题平面化。实现这一转化的常用途径是两点直线法、平行线法、垂直射影法、截面法、展开图法等。

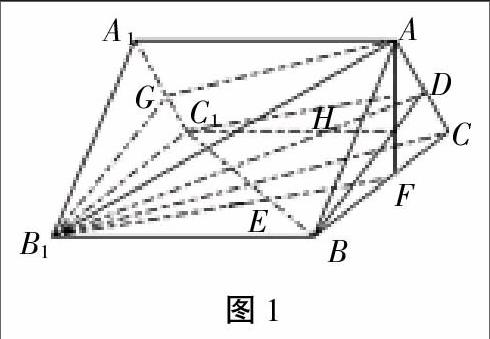
例1 如图，已知A1B1C1-ABC是正三棱柱，D是AC中点。

（1）证明AB1//平面DBC1；

（2）假设AB⊥BC1，BC=2，求线段AB1在侧面B1BCC1上的射影长。

分析：（1）欲证AB1//平面DBC1，转化为线与线（面DBC1）平行；或者面（含AB1的平面）与面BDC1平行，即图中证DE平行于AB1，或证面AGB1//平面DBC1（G为A1C1的中点）即可。

（2）先截出AB1在面B1BCC1内的射影B1F，转化为在面B1BCC1內研究而求B1F。一种是△B1BF与△C1BC相似而得；一种是过F作FH//BC1交C1C于H，则△B1FH为Rt△。设B1B为x，由Rt△B1FH的边长关系而得，另外也可通过△B1BF与△C1CD相等

求得。

二、分类思想

分类思想是一切科学研究的基本思想。一般来说，立体几何分类有两类：一是点、线、面的相互位置关系；二是线段及角度的量变引起分类。

三、基本量思想

基本量思想在立体几何问题中对确定位置、大小关系具有十分重要的意义。

例2 在三棱柱ABC-A1B1C1中，∠ACB=90°，∠BAC=30°，BC=1，AA1=，M是C1C的中点，求证：AB1⊥A1M。

分析：在化归思想指导下，根据题设与结论，易将问题转化为证明AB1在平面AA1C1C上的射影AC1与A1M垂直。再根据基本量思想，此两线的交角应由矩形AA1C1C的边长决定，因而AA1=，AC=是决定AC1与A1M垂直与否的基本量。这样，我们就能在这个特定的矩形AA1C1C中用不同的方法证明AC1与A1M垂直。另外也可在化归思想的指导下，AB1与A1M垂直，即两异面直线所成的角为90°，转化为作AB1与A1M的平行线，从而在原三棱柱的上方或下方补一个同样大小的三棱柱，再运用基本量思想验证所求的角。

四、函数与方程思想

函数与方程均为中学数学的重要内容，同时也是解决一类数学问题中经常用到的基本数学思想。

例3 如果圆柱轴截面的周长l为定值，那么圆柱体积的最大值是多少？

解：设圆柱的底面半径为r，则圆柱高h=

∴V圆柱=πr2·=lr2-2πr3

令V′=（2lr-12r2）=0，则r=或r=0（舍）

∴当l-4r=2r，即r=时，V圆柱最大=πl3

与函数概念密切联系的是方程，因此，方程的思想与函数的思想也是密切相关的。

五、数形结合思想

数形结合，即是“形”中觅“数”“数”中思“形”，把要研究问题的数量关系与空间图形结合起来。华罗庚说：“数”缺“形”少直观，“形”离“数”难入微。如根据问题的需要，可把数量关系问题化为图形性质去求解；或把图形性质问题转化为数量关系来研究。

例4 球面上有P、A、B、C四点，如果PA、PB、PC两两互相垂

直，且PA=PB=PC，那么这个球面的面积是多少？

分析：可据题构想一个棱长为a的正方体内接于半径为R的球，由对称性知识R=a/2，故S球=3πa2。

六、整体思想

整体思想是一种从全局总体出发着眼处理问题的思想方法。常用的有整体代换、圆形的补形与分割、等面积体积求距离等。

七、类比与转换思想

类比即是先从一个类似的平面几何问题出发，去探求立体几何问题。而转换就是把立体几何问题的基本元素转换到某一个或几个平面中，然后用平面几何知识来解决。

在教学中，立体几何中许多重要概念，如异面直线所成的角、直线与平面所成的角、二面角的大小都是用两相交直线所成的角来定义。它们都是通过把空间图形中许多基本元素的计算问题转换成平面图形问题来解决。常用的方法有构造含有空间图形基本元素的平面图形，利用多面体和旋转体的截面，或多面体和旋转体的侧面展开图等，这里就不再一一举例。

总之，一定要掌握好各种基本数学思想，善于融会贯通、举一反三，这样就会逐步提高数学学习能力。