一种混沌变参数粒子群优化算法

2017-03-23虎涛涛单要楠

自动化仪表 2017年3期

关键词：控制参数适应度全局

虎涛涛,单要楠

(1.电子科技大学电子科学技术研究院，四川成都 611731；2.电子科技大学数学科学学院，四川成都 611731)

一种混沌变参数粒子群优化算法

虎涛涛1,单要楠2

(1.电子科技大学电子科学技术研究院，四川成都 611731；2.电子科技大学数学科学学院，四川成都 611731)

粒子群优化算法存在易陷入局部最优、收敛精度低、进化后期收敛慢等问题，混沌粒子群优化算法利用混沌运动的遍历性、随机性、规律性特点，很好地解决了粒子群优化算法陷入局部最优的问题，但混沌初始化会破坏已收敛的种群结构。在混沌粒子群优化算法的基础上，提出了一种混沌变参数粒子群优化算法。对陷入局部最优的种群进行混沌初始化，并采取一定的规则动态改变混沌运动的控制参数，以增强或减弱混沌方程的混沌特性，既可以减轻混沌初始化对已收敛种群结构的破坏性，又能利用混沌特性摆脱种群陷入局部最优问题，提高收敛精度，从而提高算法的全局寻优能力。通过仿真测试表明，混沌变参数的粒子群优化算法能有效避免种群陷入局部最优现象，收敛快、收敛精度高，全局寻优能力优于基本粒子群优化算法。

粒子群优化算法；混沌运动；变参数；局部最优；收敛；优化

0 引言

Kennedy和Eberhart于1995年提出粒子群优化(particle swarm optimization，PSO)算法[1]。该算法具有原理简单、易于实现、收敛速度快的优点，被广泛应用于目标函数优化、自适应控制、神经网络等领域[2-3]，与其他进化算法一样，PSO算法同样存在易陷于局部最优、优化计算精度低、后期收敛慢的缺点。针对这些缺点，学者们提出了很多改进的粒子群算法[4-6]。尽管这些改进算法能解决局部最优的问题，但在收敛性能上仍存在一定的不足，效果并不理想。本文根据混沌运动的随机性、遍历性等特点[7]，提出一种混沌变参数粒子群优化算法。对典型函数的仿真测试表明，与混沌粒子群优化算法和基本粒子群优化算法相比，混沌变参数粒子群优化算法在保证算法能摆脱局部最优的基础上，收敛性能明显提高。

1 粒子群优化算法

PSO算法的思想源于对鸟群捕食行为的研究与模拟，是一种基于群体的智能优化算法。基本粒子群优化算法，又称为标准粒子群算法(standard particle swarm optimization,SPSO)，其在粒子群优化算法中引入了惯性权重系数，以平衡粒子的搜索能力，保证算法的局部寻优能力和全局寻优能力。

基本粒子群优化算法中，粒子每次通过两个值来更新自己的位置，一个为粒子自身的最优解，另一个为种群所有粒子找到的最优解，用数学方法描述如下。

假设粒子种群的群体规模为N，每个粒子在D维空间进行搜索，则xi=(xi1,xi2,...,xid)是第i个粒子的当前搜索位置，xid是第i个粒子的第d维空间位置，vi=(vi1,vi2,...,vid,...,viD)是第i个粒子的当前飞行速度，vid是第i个粒子的第d维空间飞行速度。设f(x)为目标函数，即适应度函数；pi=(pi1,pi2,...,pid,...,piD)是第i个粒子所经历的最优位置，称为个体最优；pg(pg1,pg2,...,pgd,...,pgD)是群体中所有粒子所经历的最优位置，称为全局最优，并且全局最优位置pg只有一个。设当前迭代次数为k，则粒子的当前位置xi和飞行速度vi按照以下两式来更新：

(1)

(2)

个体最优位置pi和全局最优位置pg由以下两式确定：

(3)

(4)

以上公式中：i=1,2,...N;d=1,2,...,D;w为惯性因子，用于修正自身原有飞行速度，通常在[0.1，0.9]之间取值;c1、c2为学习因子，一般取常数2;rand1、rand2为两个相互独立、并在[0，1]之间取值的随机数。

基本粒子群优化算法具有操作简单、实现容易、收敛速度快、无需确定太多参数等优点。但根据文献[2]对基本粒子群优化算法中粒子位置和飞行速度的收敛性分析可知，基本粒子群优化算法在进化后期收敛速度比较慢，收敛精度降低，容易陷入局部最优值；同时，由于粒子停滞使种群丧失多样性，会导致算法早熟收敛。混沌(Chaos)是自然界普遍存在的非线性现象，是由确定方程得到的非确定随机运动状态，具有随机性、便利性及规律性等特点，它对初始条件极度敏感，能在一定范围内不重复地遍历所有状态。本文根据混沌运动的这些特点，提出一种混沌变参数粒子群优化算法。

2 混沌变参数粒子群优化算法

混动运动变化过程看似杂乱无章，但其并不是完全混乱，而是含有内在的规律性[8]。呈现混沌状态的变量称为混沌变量，其对初值极其敏感。一个混沌变量在一定范围内有如下特点：①随机性，即它的表现同随机变量一样杂乱；②遍历性，即它可以不重复地遍历空间内的所有状态；③规律性，该变量是由确定的迭代方程确定的。Logistic方程是一个典型的混沌系统，其公式为：

xn+1=μ×xn×(1-xn)

(5)

式中：μ为混沌控制参数，其决定Logistic方程的混沌程度，μ值越大，混沌程度越高，一般在[0，4]之间取值，xn∈[0,1]。

利用混沌对初值敏感的特点，给式(5)赋i个具有微小差异的初值，即可得到i个混沌变量。

由于混沌变量的遍历性、随机性有助于增强种群的搜索能力[9]，因此，为解决基本粒子群算法中出现的陷入局部最优、收敛精度低等问题，很多学者将混沌思想和粒子群优化算法相结合，提出了混沌粒子群优化算法(chaotic particle swarm optimization,CPSO)。戴冬雪等在算法的初始阶段，对粒子的位置混沌初始化；而在算法运行过程中，根据群体适应度方差来自适应地对粒子的位置进行混沌更新[10]。张劲松等以基本粒子群优化算法的运算流程作为主体流程，当整个粒子群历史全局最优位置pg连续不变化或变化极小时，将混沌搜索机制引入其中，在以pg为中心的一定范围内进行混沌搜索，将混沌搜索得到的最优解作为新的pg，并继续原粒子群算法的求解[11]。按概率方式来决定混沌搜索的时间，在进化初期，以较小的概率进行混沌搜索；在进化后期，以接近1的概率进行混沌搜索[12]。

混沌控制参数μ越大，混沌程度越高，对种群结构的破坏性越大，在算法运行过程中，根据种群的收敛情况，动态地减小或增大控制参数μ，就可以减少对种群结构的破坏，同时摆脱陷入局部最优的困境。因此，本文提出的基于混沌变参数的粒子群优化算法的思想是：在算法运行过程中，利用群体适应度方差进行早熟收敛判断。当发现种群陷入局部最优时，保留粒子群个体最优解，混沌初始化粒子群，根据准则判断目前粒子群收敛情况，并根据一定的规则动态增大或减小混沌控制参数μ，减少对已收敛种群结构的破坏，这样在保证收敛速度的基础上，既能摆脱种群陷入局部最优的现象，又能提高收敛精度和全局优化能力，其算法具体的流程描述如下。

①初始化参数。种群规模为N，粒子搜索空间维数为D，学习因子为c1、c2,惯性因子最大值为wmax，最小值为wmin，混沌控制参数为μ，迭代次数为T。

②混沌初始化种群。随机产生一组取值区间为[0,1]的变量z1=(z11,z12,...,z1d,...,z1D)，利用Logistic方程产生(N-1)个混沌变量z2,z3,..,zN，并根据式子xi=xmin+(xmax-xmin)zi,将这N个变量映射到粒子位置取值区间[xmin,xmax]上，生成位置变量。速度变量可以根据实际情况取位置变量的百分比，根据适应度函数f(x)求出初始种群的个体最优解pi和全局最优解pg。

③根据式(1)、式(2)更新粒子位置xi和速度vi。

④根据适应度函数f(x)求出粒子的适应度，并根据式(3)、式(4)来更新个体最优解pi和全局最优解pg。

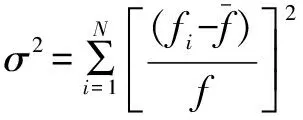
(6)

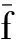
如果适应度方差σ2小于所设定的阈值且满足混沌搜索条件，则保留粒子群个体最优解，根据准则判断粒子群收敛情况，动态改变混沌控制参数，并返回步骤②。对种群重新初始化，再根据适应度函数求出粒子的适应度，并与保留的粒子群个体最优解比较，确定全局最优解；否则继续执行步骤⑥。

⑥判断是否满足终止条件或达到最大迭代次数T，满足即跳转到步骤⑦，否则返回步骤③。

⑦优化结束，输出结果。

3 仿真测试

为了验证本文提出的变参数混沌粒子群优化算法的收敛性能，现选取三个典型函数作为测试，并与混沌粒子群优化算法、基本粒子群优化算法作对比。三个典型函数分别如下：

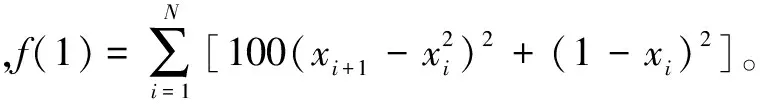
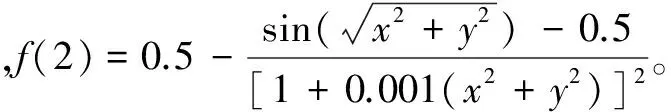
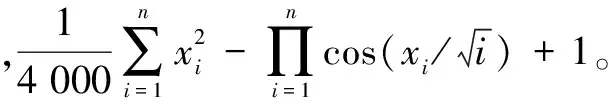
变参数混沌粒子群优化算法的初始化参数如下：种群规模N为20，位置、速度取值和三个函数后面的标注保持一致，学习因子c1、c2都为2，惯性因子最大值wmax为1、最小值wmin为0.2，混沌控制参数μ初始值为4，最大迭代次数T为1 000。各算法独立运行50次，测试函数f(1)、f(2)、f(3)的测试结果如表1所示。

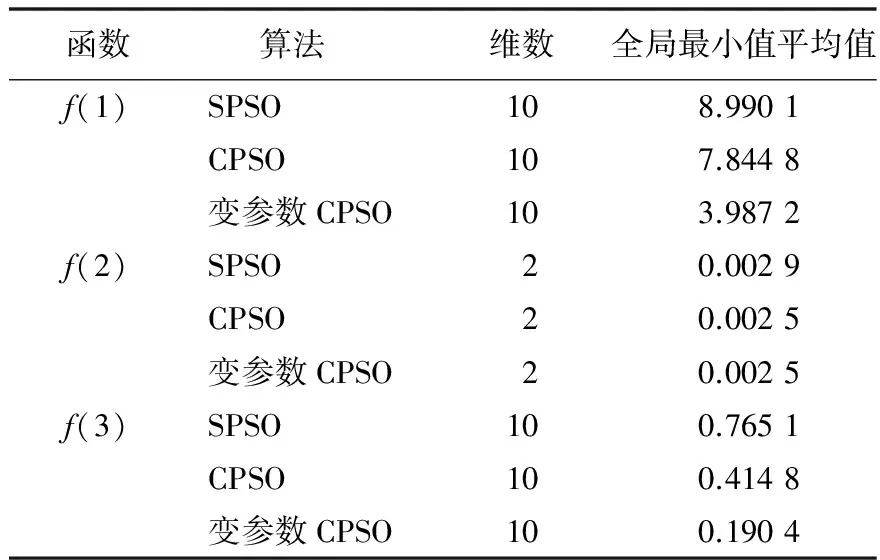
表1 三种函数的寻优测试计算结果

从表1可以看出，混沌粒子群优化(CPSO)算法和变参数混沌粒子群优化(变参数CPSO)算法都能摆脱局部最优值。CPSO算法寻优要优于SPSO算法寻优，而变参数CPSO的全局寻优能力最好、收敛精度更高，进而说明其全局寻优能力要优于混沌粒子群优化算法。

采用基本粒子群算法(SPSO)、混沌粒子群算法(CPSO)和变参数混沌粒子群算法(变参数CPSO)，得到的测试函数寻优轨迹曲线如图1所示。

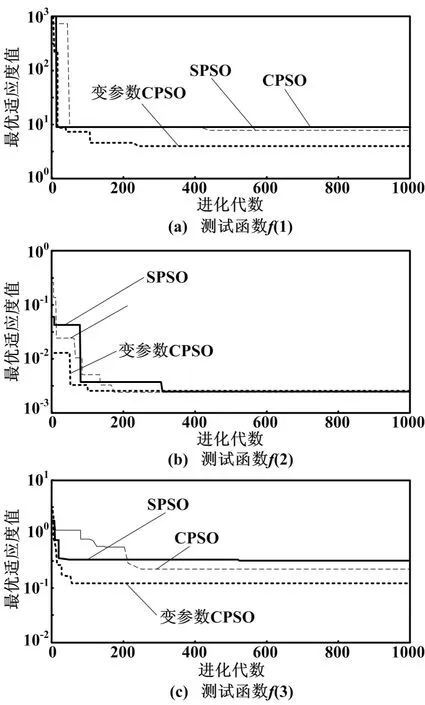
图1 测试函数寻优轨迹曲线

测试函数f(1)很难极小化函数Rosenbrock，很容易找到极小点，但是要跳出这个极小点收敛到全局最小点却十分困难。而利用混沌运动的特性，可以克服粒子群陷入局部最优的情况，图1(a)中测试函数f(1)的寻优轨迹曲线表明,CPSO算法在算法迭代450次就已收敛，而变参数CPSO在252次收敛，且收敛精度最高。图1(b)的寻优轨迹曲线表明变参数CPSO比CPSO算法收敛快。图1(c)中测试函数f(3)的寻优轨迹曲线表明,CPSO算法在算法迭代263次就已收敛，而变参数CPSO在85次收敛，且收敛精度最高。以上数据充分说明，无论收敛性能，还是克服种群摆脱局部最优性能，采用变参数CPSO算法寻优都优于采用CPSO算法和SPSO算法寻优。变参数CPSO算法既可以保证种群摆脱局部最优的问题，又可明显改善其收敛性，提高算法的全局寻优能力。

4 结束语

混沌变参数粒子群优化算法是在混沌粒子群算法的基础上，通过动态改变Logistic方程的混沌控制参数，使算法在迭代过程中根据种群收敛状态及时增强或减弱混沌运动，以降低对已收敛种群的破坏。根据仿真测试，混沌变参数粒子群优化算法既保留了混沌粒子群优化算法的优点，又保持了粒子群体的多样性，可快速跳出局部最优点，寻找全局最优解，有效提高了算法的全局寻优能力和收敛性能。

[1] KENNEDY J,EBERHART R C. Particle swarm optimization[C]//

Proceedings of IEEE International Conference on Neural Networks,Piscataway(USA):IEEE Press,1995:1942-1948.

[2] 宫玉琳,永磁同步电动机伺服系统自适应逆控制策略研究[D]. 长春：长春理工大学,2013.

[3] GRIMALDI E A,GRIMACCIA F,MUSSETTA M,et al. PSO as an effective learning algorithm for neural network applications[J]. Computational Electromagnetic and Its Applications,2004(3):557-560.

[4] LI J W,CHENG Y M,CHEN K Z. Chaotic particle swarm optimization algorithm based on adaptive inertia weight[C]//Control and Decision Conference. Beijing:IEEE,2014:1310-115.

[5] YAN Z C,LUO Y S. A particle swarm optimization algorithm based on simulated annealing[J]. Advanced Materials Research,2014,989(1):2301-2305.

[6] PAN T S,DAO T K,CHU S C. Hybrid particle swarm optimization with bat algorithm[M]. Switzerland : Springer International Publishing,2015:37-47.

[7] YANG D X,LI G,CHENG G D. On the efficiency of chaos optimization algorithms for global optimization[J]. Chaos,Solions and Fractals,2007,34(4) :1366-1375.

[8] LU H J. A new optimization algorithm based on Chaos[J]. Zhejiang University Science A,2006,7(4) :539-542.

[9] TAVAZOEI M S,HAERI M. An optimization algorithm based on chaotic behavior and fractal nature[J]. Journal of Computational and Applied Mathematics,2007,206(2) :1070-1081.

[10]戴冬雪,王祁,阮永顺,等. 基于混沌思想的粒子群优化算法及其应用[J]. 华中科技大学学报,2005,33(10):53-55.

[11]张劲松,李歧强,王朝霞. 基于混沌搜索的混合粒子群优化算法[J]. 山东大学学报, 2007,37(1):47-50.

[12]杨俊杰，周建中，喻菁，等. 基于混沌搜索的粒子群优化算法[J]. 计算机工程与应用,2005(16):69-71.

A Chaotic Particle Swarm Optimization Algorithm with Variable Parameters

HU Taotao1,SHAN Yaonan2

(1.Institute of Electronic Science and Technology,University of Electronic Science and Technology,Chengdu 611731,China；2.School of Mathematical Sciences,University of Electronic Science and Technology,Chengdu 611731,China)

Easy to fall into local optimum,low convergence precision and slow late evolutionary convergence rate are the main problems of particle swarm optimization algorithm,chaotic particle swarm optimization algorithm well solves the problem of falling into local optimum for particle swarm optimization algorithm by using the ergodicity,randomness and regularity of chaotic motion. However,chaos initialization may destroy the structure of population converged;based on the chaotic particle swarm optimization algorithm,a chaotic particle swarm optimization algorithm with variable parameters is proposed. Chaotic initialization is conducted for the population that trapped into local optimum,and certain rules are adopted to dynamically change the control parameters of chaotic motion,to enhance or weaken the chaotic characteristics of the chaotic equation. The destruction of the converged population can be reduced,and the problem of falling into local optimum can be got rid of by using chaotic characteristics,thus the convergence precision and the capability of global optimization are improved. The simulation tests show that the phenomenon of population trapped into local optimum can be effectively avoided by the algorithm proposed,the convergence precision is high,and the capability of optimization is better than of the basic particle swarm optimization algorithm.

Particle swarm optimization algorithm; Chaos motion; Variable parameter; Local optimum; Convergence; Optimization