不确定分数阶Colpitts系统的混沌同步研究
2017-03-23李贤丽窦雪莹赵昱阳
李贤丽,窦雪莹,赵昱阳
(东北石油大学电子科学学院,黑龙江 大庆 163318)
不确定分数阶Colpitts系统的混沌同步研究
李贤丽,窦雪莹,赵昱阳
(东北石油大学电子科学学院,黑龙江 大庆 163318)
分数阶混沌系统在信息加密等领域具有广泛的研究价值。通过理论推导和数值仿真两方面的研究,采用分数阶系统的稳定性定理,对选取的分数阶多涡卷混沌Colpitts振荡电路系统的动力学特性进行了详细的分析,并计算出了该系统处于混沌态时的阶数范围。研究结果证明,当系统作混沌运动时,其混沌吸引子的形态存在特殊的演变过程,逐渐从单涡卷混沌吸引子演变为多涡卷混沌吸引子。将自适应技术和参数辨识技术应用到混沌系统的同步控制中,在参数不确定的情况下,基于Lyapunov函数稳定性理论,设计了合理的控制器和估计参数自适应律。利用不确定参数的自适应同步法,分别实现了系统在阶数相同和阶数不同两种情况下的完全同步以及对未知参数的辨识。该结果对于参数未知混沌系统的同步研究具有重要意义。
信息安全; 自适应技术; 分数阶系统; Colpitts系统; Lyapunov稳定性理论
0 引言
近年来,人们热衷于对分数阶混沌系统的研究。在信息安全、保密通信等领域,分数阶混沌系统正成为非线性科学应用的新方向[1],而混沌系统的同步控制技术是应用过程中需要解决的关键问题。到目前为止,已提出许多同步方法,如驱动-响应控制法[2]、自适应控制法[3-5]和滑模控制法[6]等。上述方法都只是针对确定性系统进行的研究,对不确定性系统的同步[7-10]研究却很少,但不确定性系统在实际中应用广泛。因此,本文选取分数阶的Colpitts振荡电路系统为研究对象,对系统随参数变化的运动规律进行研究,并且采用自适应同步法,对分数阶混沌的不确定性系统,分别实现了阶数相同和阶数不同两种情况下的同步。
1 分数阶混沌Colpitts系统分析
1.1 分数阶微积分定义
(1)
式中:m为正整数;a>0;Γ(·)为Gamma函数。
根据分数阶系统稳定定理,通过理论计算求解分数阶系统在混沌状态时的阶数范围。采用预估-校正解法,对分数阶系统进行数值计算,全面了解系统的参数、阶数等因素对其动力学性能的影响。
1.2Colpitts振荡电路系统模型
对典型Colpitts振荡电路系统进行参数归一化处理[11],并引入分段线性三角波函数[12],再增添一维线性控制器,简化参数后可得到多涡卷混沌Colpitts系统。本文研究Colpitts系统相应的分数阶混沌系统,其数学模型可描述为:
(2)
式中:α1,α2,α3,α4∈(0,1)。
(3)
式中:K为正整数;p>0;q∈(0,p)。
分段线性三角波函数曲线图(N=3)如图1所示。

图1 分段线性三角波函数曲线图(N=3)
根据文献[12],通过对比系统随参数q变化的分岔图和Lyapunov指数谱可知,q值越小,混沌吸引子所形成的涡卷分布越均匀。因此,本文选取q=0.02p。
1.3 动力学性质分析
选取分数阶混沌Colpitts系统中的分段线性三角波函数的参数为M=2、N=1、p=1、q=0.02,系统初值为(0.2,0.2,0,0),利用预估-校正解法,对系统进行数值计算,得到的系统状态变量随参数μ变化的分岔图如图2所示。

图2 分岔图
当μ分别为0.4和1时,系统二维相图如图3所示。

图3 系统二维相图
当μ=(1,2]时,系统处于混沌态,分别取参数μ=1.11、μ=1.13、μ=1.39,并对这些参数下的混沌系统进行仿真。从所得到的二维相图可以观察到,随着参数的变化,混沌吸引子的形态也发生了明显的变化,在平面x-y上,其由单涡卷向五涡卷演变,具体形态变化如图4所示。

图4 x-y平面上二维相变化图
在平面y-w上,混沌吸引子由(1×3)涡卷向(5×3)涡卷演变,具体形态变化如图5所示。
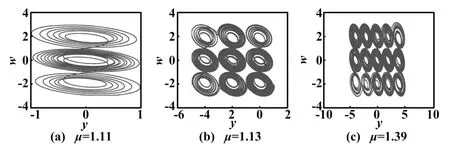
图5 y-w平面上二维相变化图
对分数阶混沌Colpitts系统的稳定定态进行稳定性分析。系统在平衡点处的Jacobian矩阵为:
(4)
(5)
令混沌系统中各状态变量对时间的导数均为0,可得fM(y)=0、fN(w)=0、z=0、x=-y,进而求得平衡点以及平衡点处的特征方程。根据Routh-Hurwitz稳定判据,利用数值计算可知,当参数满足μ>0.626 3时[13],系统处于混沌状态。
由分数阶系统稳定性定理可知,要确保系统在平衡点处渐进稳定,需要满足特征根(λ1,λ2,λ3,λ4)均在|arg(λ1)|>πα/2、α=max(q1,q2,q3,q4)=1,2,3,4条件下成立。通过数值计算可得,当分数阶超混沌Colpitts系统的阶数为(q1,q2,q3,q4)∈[0.919 1,1)时,满足条件。
2 分数阶混沌Colpitts系统的同步
2.1 相同阶数情况
设定式(2)为驱动系统,响应系统可以描述为:
(6)

设系统误差变量e1=x2-x1、e2=y2-y1、e3=z2-z1、e4=w2-w1,由此可得误差系统为:
(7)
根据驱动系统(2)和响应系统(6),为了保证误差系统(7)在t→∞时渐进稳定,可以对控制变量和估计参数自适应率分别进行设计,如式(8)所示:
(8)
选取估计参数自适应律为:

(9)
根据Lyapunov稳定性判定定理可知,在选取合适的控制变量和估计参数自适应律的情况下,误差系统趋于0,驱动系统和响应系统可实现同步。
基于改进的Adams-Bashforth-Moulton理论算法,分别选取驱动系统初值为x1(0)=0.2、y1(0)=0.2、z1(0)=0、w1(0)=0,响应系统初值为x2(0)=-0.6、y2(0)=-0.45、z2(0)=1、w2(0)=2,估计参数初值为μ(0)=0.01,系统阶数取α1=α2=α3=α4=0.92。阶数相同时的同步仿真结果如图6所示。随着时间的变化,在控制变量和估计参数自适应率的共同作用下,两系统间的误差逐渐趋于0,未知参数μ也逐渐趋于给定值,从而实现了驱动系统和响应系统之间的同步。

图6 阶数相同时的同步仿真结果
2.2 不同阶数情况

定义驱动系统为:
(10)
式中:β1,β2,β3,β4∈(0,1]。
由分数阶微积分定义及以上定理,对上式进行转化,可以得到:
(11)
经过如上转换,不同阶数混沌Colpitts系统的同步问题就转变为相同阶数的异结构超混沌系统(2)和(11)之间的同步问题。
在响应系统(2)中加入控制变量μ=[μ1,μ2,μ3,μ4]T。设系统误差变量为e1=x1-x3、e2=y1-y3、e3=z1-z3、e4=w1-w3,由此可得到误差系统:
(12)
同理,分别设计误差系统(12)的控制变量和估计参数自适应率:
(13)
(14)
将控制器和估计参数自适应律代入误差系统,整理后,验证了此设计的合理性。
分别选取驱动系统初值x3(0)=-0.285、y3(0)=-0.255、z3(0)=1、w3(0)=2,阶数β1=β2=β3=β4=0.919 7,响应系统初值x1(0)=0.2、y1(0)=0.2、z1(0)=0、w1(0)=0,阶数α1=α2=α3=α4=0.92,估计参数初值为μ(0)=0.01。阶数不同时的同步仿真结果如图7所示。随着时间的变化,在控制变量和估计参数自适应率的共同作用下,驱动系统和响应系统之间的误差逐渐趋于0,未知参数μ也逐渐趋于给定值,从而实现了同步。

图7 阶数不同时的同步仿真结果
3 结束语
本文对分数阶Colpitts混沌系统进行了理论分析和数值计算,得出系统随着参数的变化,存在稳定态、周期态和混沌态等多种运动状态。当阶数的取值范围为(q1,q2,q3,q4)∈[0.919 2,1]时,系统处于混沌态,且系统混沌吸引子的形态在各个平面上表现出明显的变化趋势,由单涡卷逐渐演变为多涡卷。当系统参数不确定时,基于Lyapunov稳定性定理,构造控制器和估计参数自适应律。利用自适应同步法,分别实现了相同阶数和不同阶数两种情况下的分数阶混沌Colpitts振荡电路系统的完全同步。所得到的仿真结果证明了该方法的有效性以及设计的合理性。
[1] ARMAN K B,KIA F,NASER P,et al.A chaotic secure communication scheme using fractional chaotic system based on an extended fractional Kalman filter[J].Communication in Nonlinear Science and Numerical Simulation,2009,14(3):863-879.
[2] LI C,DENG W.Chaos synchronization of fractional-order differential systems[J].International Journal of Modern Physics B,2006,20(7):791-803.
[3] ZHANG R X,YANG S P.Adaptive synchronization of fractional-order chaotic systems via a single driving variable[J].Nonlinear Dynamics,2011,66(4):831-837.
[4] ODIBAT,ZAID M.Adaptive feedback control and synchronization of nonidentical chaotic fractional-order systems[J].Nonlinear Dynamics,2010,60(4):479-487.
[5] ZHANG R,YANG S.Stabilization of fractional-order chaotic system via a single state adaptive-feedback controller[J].Nonlinear Dynamics,2012,68(1):45-51.
[6] CHEN D,LIU Y,MA X,et al.Control of a class of fractional-order chaotic systems via sliding mode[J].Nonlinear Dynamics,2012,67(1):893-901.
[7] 金鑫,江铭炎.基于非线性控制的异结构混沌同步控制[J].山东大学学报(工学版),2007,37(5):78-83.
[8] DAS S.A modified adaptive control method for synchronization of some fractional chaotic systems with unknown parameters[J].Nonlinear Dynamics,2013,73(1),907-919.
[9] 黄丽莲,齐雪.基于自适应滑模控制的不同维分数阶混沌系统的同步[J].物理学报,2013,62(8):53-59.
[10]董俊,张广军,姚宏,等.异结构的分数阶超混沌系统函数投影同步及参数辨识[J].电子与信息学报,2013,35(6):1371-1375.
[11]MAGGIO G,FEO O,KENNEDY M.Nonlinear analysis of the colpitts oscillator and applications to design[J].IEEE Transactions on CAS,1999,46(9):1118-1130.
[12]禹思敏.用三角波序列产生三维多涡卷混沌吸引子的电路实验[J].物理学报,2005,54(4):1500-1509.
[13]包伯成,刘中,许建平,等.基于Colpitts振荡器模型生成的多涡卷超混沌吸引子[J].物理学报,2010,59(3):1540-1548.
Research on the Chaotic Synchronization for the Fractional-Order Colpitts System with Uncertain Parameters
LI Xianli,DOU Xueying,ZHAO Yuyang
(College of Electronics Science,Northeast Petroleum University,Daqing 163318,China)
In information encryption field,the fractional-order chaotic systems have extensive research value.Through the research on theoretical derivation and numerical simulation,by adopting the stability theorem of fractional-order system,the dynamics characteristics of the selected fractional-order multi-scroll chaotic Colpittsoscillation circuit system are analyzed in detail,and the range of the orders in which the systemis in a chaotic state is calculated.The results of research show that when the system is in chaotic motion,the form of the chaotic attractor has a specific transformation process;the single-scroll chaotic attractor gradually turns into multi-scroll chaotic attractor.Adaptive control technology and parameter identification technology are used in the synchronous control of chaotic systems,in the case of uncertain parameters,and based on the Lyapunov stability theory;a reasonable controller is designed,and the parameter adaptive laws are estimated.By using the adaptive synchronization under uncertain parameters,the full synchronization of the fractional-order chaotic systems with the same order and a different order and the identification of the unknown parameter are realized respectively.The results are more useful for researching the synchronization of chaotic systems with unknown parameters.
Information security; Adaptive technology; Fractional-order system; Colpitts system; Lyapunov stability theory
黑龙江省自然科学基金资助项目(A201402)、黑龙江省教育厅科学技术研究基金资助项目(12541064)
李贤丽(1971—),女,博士,教授,主要从事非线性动力学及混沌控制方向的研究。E-mail:lxl7158@163.com。 窦雪莹(通信作者),女,在读硕士研究生,主要从事分数阶混沌同步方向的研究。E-mail:735714684@qq.com。
TH13;TP273
A
10.16086/j.cnki.issn1000-0380.201703006
修改稿收到日期:2016-11-29
