微纳卫星姿态机动的变论域模糊PID控制

张 悦,林 都,鲜 浩,林云海

(中北大学计算机与控制工程学院，山西 太原 030051)

微纳卫星姿态机动的变论域模糊PID控制

张 悦,林 都,鲜 浩,林云海

(中北大学计算机与控制工程学院，山西 太原 030051)

为了简化计算，满足实时处理的要求，建立了微纳卫星的姿态角动力学模型，并应用欧拉角参数描述运动学模型。针对微纳卫星系统的时变、环境外力矩干扰等因素，同时考虑到系统参数不确定性问题，设计了变论域模糊PID控制律的姿态控制器。不考虑解耦运算，分析了控制器的动态变化参数对姿态稳定控制性能的影响。基于MATLAB/SIMULINK对该系统进行了仿真验证。仿真结果表明，在卫星姿态控制方面，该控制方法具有稳定性好、响应快速、系统超调量小的特点，能够使微纳卫星完成对目标姿态的机动控制，实现对系统姿态的有效控制。

模糊控制； PID控制; 航天技术； 微纳卫星； 高斯分析； 变论域； 仿真

0 引言

随着航天技术的高速发展，卫星在现代通信、国防建设和科技研究等领域发挥着越来越重要的作用。微纳卫星以其质量轻、体积小、技术新、制造周期短等特点，在航天任务中得到了广泛的应用。微纳卫星控制的关键技术之一是姿态控制系统设计，国内外很多学者在这方面开展了大量研究，并取得了一系列成果[1-8]。因此，设计有效的控制策略以实现对微纳卫星的姿态控制，已成为航天领域广泛关注的热门课题。

经典PID控制律具有稳定性好、算法成熟、控制参数相互独立等优点，长久以来被认为是理想的控制策略。但是在实际应用中，卫星姿态系统的结构具有非线性、强耦合等特性。当系统内部结构或者外部环境发生变化时，PID控制律对于非线性、不确定的复杂系统难以达到理想的控制效果[4-6]。文献[6]应用非线性控制模块实现姿态参数的优化设计，文献[7]基于遗传算法实现算法参数调节。尽管以上方法可以达到控制目的，但是在一定程度上计算相对复杂，无法满足实时处理的要求。

本文将模糊规则和PID调节相结合，引入变论域控制算法，保持了PID控制算法静态误差小的优势，又实现了控制灵活、快速的特点，对非线性复杂星体姿态控制系统实现了良好的控制。仿真结果验证了控制律能够达到理想的控制效果。

1 微纳卫星数学模型

以一类微纳卫星为研究对象，假设卫星为刚体，且考虑外部扰动作用，具有推力器执行机构卫星的动力学模型为：

(1)

I=[IxIyIz]为卫星转动惯量矩阵;ω=[ωxωyωz]T为星体的角速度；u=[u1u2u3]T为星体所受控制力矩；T=[Td1Td2Td3]T为外界干扰力矩。

(2)

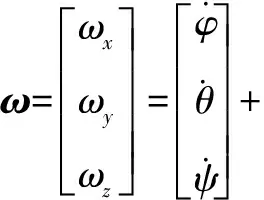
(3)

忽略转动惯量矩阵中的惯量积，线性化得到所用的卫星姿态运动方程，将式(2)代入式(1)得到：

卫星的姿态运动方程为二阶非线性方程，且姿态的滚动角φ、俯仰角θ、偏航角ψ三通道相互耦合[3-5]。通过解耦实现对卫星姿态的控制比较复杂，且无法满足实时处理的要求。针对微纳卫星的复杂结构设计模糊PID控制律，分别对模糊PID姿态控制系统进行数学仿真。微纳卫星姿态控制系统结构如图1所示。

图1 系统结构图

2 变论域模糊PID控制器

2.1 控制器结构设计

模糊PID控制器主要由模糊控制系统和可控式参数PID系统组成[13-14]。目前，应用广泛的是二维模糊控制器，其采用误差及误差变化率作为输入变量，修正参数变化量作为输出变量。其基本原理是以系统误差e和误差变化率ec作为输入，参数变化量ΔkP、ΔkI、ΔkD作为输出， 以满足不同时刻对参数的整定要求。根据模糊规则产生相应的输出，并在PID控制器初始参数的基础上进行实时调节，能提高系统的控制性能，以满足不同阶段对PID控制器参数的不同要求[14-16]。模糊PID控制器结构如图2所示。

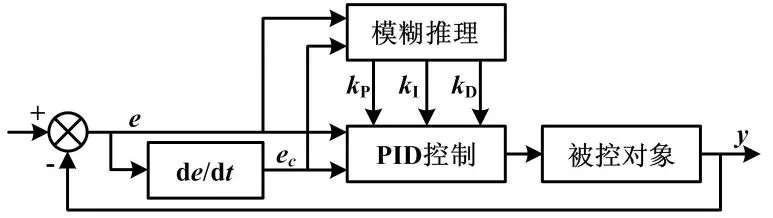
图2 模糊PID控制结构图

变论域模糊PID控制在模糊PID控制的基础上，增加了一个论域调整机构，误差e和误差变化率ec的初始论域[-E,E]与自适应规律产生的伸缩因子α(x)相乘，得到满足控制状况的新论域[3-4]。

增量关系表达式为：

(5)

当Δx→0时，得到微分方程：

(6)

分离变量可得：

(7)

其实际论域为：

2.2 伸缩因子设定

如何选取伸缩因子是变论域思想的关键问题。依据各类文献资料[12-13]，目前有两种常用的构造伸缩因子的方法。一种方法是由模糊规则确定论域的伸缩因子，另外一种方法是基于误差或者误差变化率的函数确定伸缩因子。本文设计变论域模糊PID控制误差e和误差变化率ec作为输入变量，参数变化率作为输出变量，采用变化量函数确定伸缩因子，作为双输入单输出系统，构造输入误差e和误差变化率ec的连续函数并确定伸缩因子αe、αec、βu。输入误差e的基本论域e=[-emax,emax]，误差变化率ec的基本论域ec=[-ecmax,ecmax]。引入伸缩因子αe后，误差e和误差变化率ec的论域变换为e=[-αeemax,αeemax]、ec=[-αeecmax,αeecmax]。同理，输出的基本论域则变换为u=[-βuμmax,βuμmax]。

2.3 控制器设计

模糊控制规则以满足系统输出响应的静态特性为目标，是设计控制系统的关键。根据PID控制器中每个参数对系统动态及稳态控制的影响效果，建立相应的模糊规则[1]。模糊规则需满足原则: 当|e|较小时，减小系统的稳态误差，选取较大的kP、kI、kD，可以保证系统的动态性能减小稳态误差；当|e|适中时，适当减小kP，选取适中的kI、kD，可有效地减小系统的超调量；当|e|较大时，加快系统的动态响应，选取较大的kP、较小的kD，为防止出现较大的超调，选取较小的kI(或为0)[15-19]。根据模糊控制原则，同时考虑参数对控制系统的影响效果，能有效地限制积分作用，避免产生较大的超调量。令kI=0，因此PID部分选择PD控制。

建立模糊PID控制器应对输入输出量进行模糊化处理，以误差e、误差变化率ec作为模糊推理的输入部分，参数变化率ΔkP、ΔkD作为模糊推理的输出部分。设定e、ec的论域均为[-3，3]；ΔkP、ΔkD基本论域均为[-6,6]。对于输入、输出变量均采用模糊子集：{NB,NM,NS,ZO,PS,PM,PB}定义隶属度函数，采用变化量函数构造基本论域的伸缩因子αe=1-0.5e-0.5e2、αec=1-0.5e-0.5ec2、βkP=0.1|e|、βkD=0.5|e|，e和ec采用三角隶属函数，ΔkP、ΔkD采用高斯分布函数，通过MATLAB得到参数隶属函数。

采用“If A and B then C”的推理条件语句，结合专家的控制实践经验，制定的ΔkP、ΔkD模糊控制规则表如表1、表2所示。

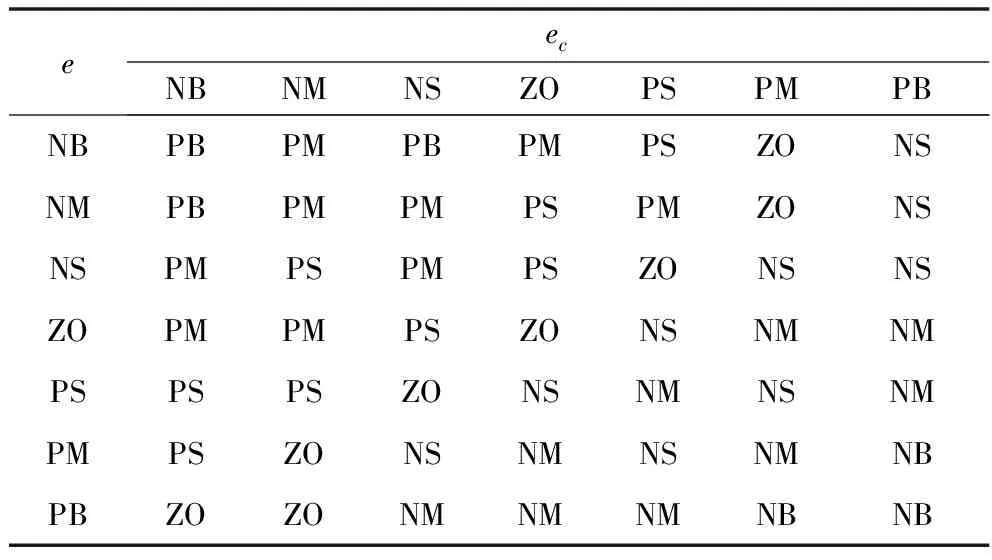
表1 ΔkP模糊控制规则

表2 ΔkD模糊控制规则

模糊推理采用Mamdani算法：令e=A、ec=B，则R=(x,y)=A(x)×B(y)。

kP的模糊推理可表示为：

(8)

同理可得kD的模糊推理表达式，加权平均解模糊化法求解公式如下：

采用SIMULINK工具箱中的模块，在基础的PID控制模块上，采用变论域自适应模糊PID模块。

3 数值仿真

设置卫星运行高度为450 km，星体的转动惯量为:

(9)

考虑作用在卫星轨道的干扰力矩为:

(10)

卫星的起始角速度和姿态角分别设定为：ωx=0.01 rad/s、ωy=0.02 rad/s、ωz=0.025 rad/s、φ(0)=0.4 rad、θ(0)=0.2 rad、ψ(0)=-0.2 rad。目标角速度及姿态角速度为：ωx=ωy=ωz=0 rad/s、φ(0)=θ(0)=ψ(0)=0 rad。

调整参数设置，分别仿真卫星的姿态角、角速度和控制力矩的时间响应情况。在变论域模糊PID控制作用下，星体的角速度变化曲线与姿态角变化曲线分别如图3、图4所示。可以看出，系统约在4 s收敛到0，达到目标角速度与目标姿态角。整个控制过程中,

卫星的姿态变化曲线平滑,没有发生剧烈变化，调节时间短、超调量小、稳态精度高、控制效果良好。

图3 角速度变化曲线

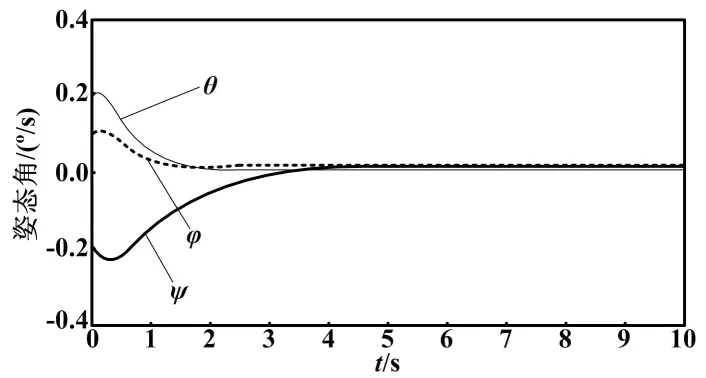
图4 姿态角变化曲线

在变论域模糊PID控制作用下，星体控制力矩变化曲线如图5所示。控制力矩的初始幅值较小，很快达到稳定状态。转动惯量的变化对其姿态机动效果几乎没有影响，可以实现微纳卫星系统的高精度控制。

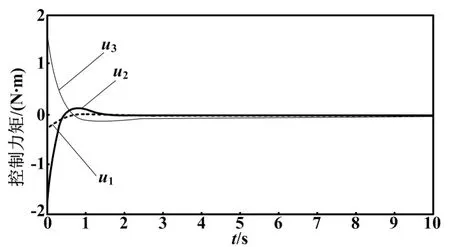
图5 控制力矩变化曲线

4 结束语

本文首先介绍了卫星姿态控制的相关知识，分析其模型特点，然后针对微纳卫星姿态控制，提出了变论域模糊PID控制方案。引入伸缩因子，在MATLAB/SIMULINK环境中搭建了该控制算法。结果表明：对于具有耦合性强、非线性特性的微纳卫星姿态控制

系统，提出的控制方案能够满足系统对目标姿态的机动控制，控制系统在响应中具有良好的稳态精度下，可快速达到渐进稳定状态，实现较好的控制效果。该控制器设计简单、方便，可应用到微纳卫星姿态控制系统中。

[1] 王辚,张科. 基于MATLAB的自整定模糊PID控制系统[J]. 探测与控制学报,2008(2):73-76.

[2] 李洪兴. 变论域自适应模糊控制器[J]. 中国科学E辑:技术科学,1999(1):32-42.

[3] 李良峰. 变论域模糊控制算法研究[D].成都:电子科技大学,2008.

[4] 姜艳. 挠性卫星自适应模糊变结构控制的研究[D].哈尔滨:哈尔滨工业大学,2008.

[5] WANG L X. Stable adaptive fuzzy control of nonlinear systems[J].IEEE Transactions on Fuzzy Systems,1993,1(2):140-151.

[6] Sousa J M.Fuzzy predictive control applied to an air-conditioning system[J].Control Engineering Practice,1997,5(10):1340-1410.

[7] 李源,吴宏悦,吴杰. 基于遗传算法PID整定的卫星姿态控制研究[J]. 中国空间科学技术,2007(4):66-71.

[8] TONG S C,WANG T,LI Y M. A combined backstepping and stochastic small-gain approach to robust adaptive fuzzy output feedback control[J]. IEEE Transaction on Fuzzy System,2013,21(2):310-321.

[9] 王蜀泉. 基于模糊控制的卫星姿态控制方法研究[D].北京：中国科学院研究生院(空间科学与应用研究中心),2005.

[10]余涌涛,梁加红. 基于SIMULINK的卫星姿控系统的仿真实现[J]. 计算机仿真,2006(11):71-74.

[11]徐燕. 微小卫星三轴稳定姿态控制系统设计[D].南京：南京航空航天大学,2005.

[12]谢祥华. 微小卫星姿态控制系统研究[D].南京:南京航空航天大学,2007.

[13]REN W,NATHAN S. Distributed coordination architecture for multirobot formation control[J].Robotics and Autonomous Systems,2008,56(2):324-330.

[14]SUI S,TONG S C,LI Y M. Adaptive fuzzy backstepping output feedback tracking control of MIMO stochastic pure-feedback nonlinear systems with input saturation[J]. Fuzzy Sets and Systems,2014,25(4):20-41.

[15]杨思亮,徐世杰. 柔性航天器大角度姿态机动的变论域分形控制[J]. 哈尔滨工业大学学报,2011(11):136-140.

[16]李洪兴，苗志宏，王加银.非线性系统的变论域自适应稳定控制[J].中国科学E辑,2002,32(2): 211-223.

[17]董恺琛,赵开春,赵鹏飞,等.微纳卫星姿控软件实时测试系统[J]. 光学精密工程,2013(8):2008-2015.

[18]乔建忠,郭雷,雷燕婕,等.微纳卫星姿态控制系统的精细抗干扰容错控制方法[J]. 中国科学:信息科学,2012(11):1327-1337.

[19]殷云华,陈闽鄂,郑宾,等.基于Matlab的模糊控制器设计及仿真[J]. 控制工程,2007(5):488-490.

Variable Universe Fuzzy PID Control for Attitude Maneuver of Nanosat

ZHANG Yue,LIN Du,XIAN Hao,LIN Yunhai

(School of Computer and Control Engineering,North University of China,Taiyuan 030051,China)

In order to simplify the calculation and satisty the requirement of real-time processing,the attitude angle dynamics model of nanosat is established,and the kinematics model is described by using Euler angle parameters. Aiming at the time varying and environment external torque disturbances,and considering the uncertainty of the system parameters,the attitude controller of variable universe fuzzy PID control has been designed;without considering the decoupling calculation,the influence of the dynamic variation parameters of the controller on the stably control performance of attitude. The simulation and verification of the system are carried out based on Matlab/simulink. The simulation results verify the correctness,in attitude control of the satellite,this control method features good stability, fast response and small overshoot;makes nanosat complete the target attitude maneuver,and achieve the effective control of the systematic attitude.

Fuzzy control; PID control; Astronautical technology; Nanosat; Gaussian distribution; Variable universe; Simulation

中国人民解放军总装备部预先研究基金资助项目(9140A20040514BQ04294)

张悦(1992—)，男，在读硕士研究生,主要从事航天器导航与控制方向的研究。E-mail:qingyixuanyuan@163.com。 林都(通信作者)，男，博士，教授，主要从事系统建模与仿真技术的研究。E-mail:lindu@nuc.edu.cn。

TH7;TP27

A

10.16086/j.cnki.issn1000-0380.201703001

修改稿收到日期：2016-06-16