基于Cosserat连续体理论的疲劳寿命概率可靠性分析

任远++尹进++张成成++侯乃先++张盛++陈飙松

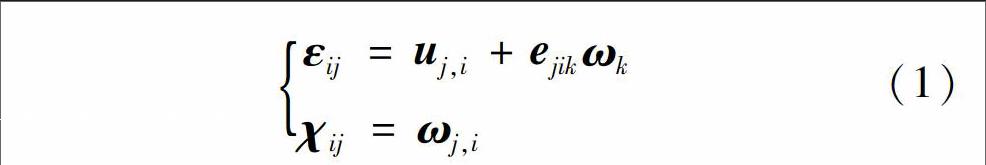
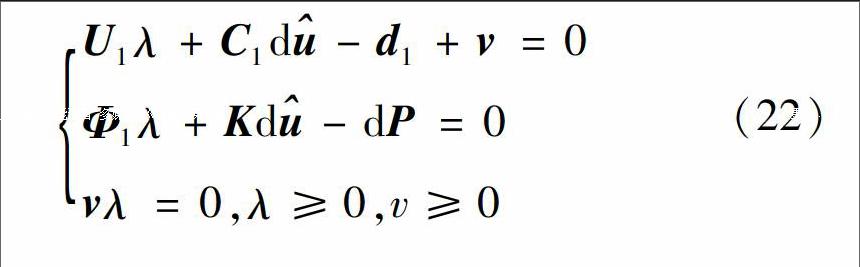
摘要： 基于Cosserat连续体理论建立考虑应变梯度效应的粉末高温合金弹塑性模型.该模型考虑微尺度长度效应，并能消除缺陷局部化问题求解时的网格依赖性.基于参变量变分原理提出一种高效的求解方法，该方法将原非线性问题转化为互补问题求解，可大大提高求解效率和收敛性.针对一种假想涡轮盘模型，将Cosserat尺度参数和Basquin斜率作为随机变量，分别采用蒙特卡洛法与二阶矩法进行疲劳寿命概率可靠度计算.结果表明二阶矩法在保证精度的情况下具有较高的效率.

关键词： 应变梯度理论； 粉末合金； 尺度效应； 弹塑性； 参变量变分原理； 涡轮盘； 不确定性； 可靠度方法

中图分类号： TB33文献标志码： B

Probabilistic reliability analysis of fatigue life based on

Cosserat continuum theory

REN Yuan1， YIN Jin2， ZHANG Chengcheng1， HOU Naixian1，

ZHANG Sheng2， CHEN Biaosong2

（1. AVIC Commercial Aircraft Engine Co.， Ltd.， Shanghai 201108； 2. State Key Laboratory of Structural Analysis for

Industrial Equipment， Dalian University of Technology， Dalian 116024， Liaoning， China）

Abstract： Considering the strain gradient effect， an elastoplastic model of powder metallurgy superalloy is proposed on the basis of Cosserat continuum theory. The model takes into account the effect of microscale length and can eliminate the mesh dependence when solving the problem of localization of defects. Based on parametric variational principle， an efficient solution method is proposed. The original nonlinear problem is transformed into the complementary problem to solve by the method， which can greatly improve the efficiency and convergence of the solution. As to a hypothetical turbine disk model， the Cosserat scale parameter and the Basquin slope are considered as random variables， and Monte Carlo method and the secondmoment method are used to calculate the probabilistic reliability of fatigue life. The results show that the efficiency of secondmoment method is high in the case of ensuring accuracy.

Key words： strain gradient theory； powder alloy； scale effect； elastoplasticity； parametric variational principle； turbine disk； uncertainty； reliability method

收稿日期： 2017[KG*9〗01[KG*9〗03修回日期： 2017[KG*9〗02[KG*9〗01

基金項目： 国家自然科学基金（11232003， 91315302）；国家重点基础研究发展计划（“九七三”计划）（2010CB832704）；高等学校学科创新引智计划（B08014）；教育部博士点基金（20130041110050）；上海市科学技术委员会科研计划（13DJ1400200）

作者简介： 任远（1982—），男，四川南充人，高级工程师，博士，研究方向为航空发动机结构可靠性，（Email）renyuan@acae.com.cn0引言

航空发动机是飞机的心脏，其中涡轮盘等热端部件，由于处在高温的恶劣工作条件下，其故障最多，是影响发动机可靠性的主要因素.实际的不确定性因素，一是来自于外部因素的影响，如载荷和环境等的不确定性；二是来自于内部因素的影响，如材料性能的分散性.在起飞—巡航—着陆的多次循环中，部件材料实际上经受着疲劳作用.随着航空发动机的发展，机械应力越来越高，使用条件越来越恶劣，疲劳问题也越来越突出.因此，疲劳寿命评估和可靠性分析是构件设计、防止失效、解除对发动机使用破坏的忧虑所必须进行的一项重要工作.相关学者[14]进行大量的研究工作，提出多种疲劳可靠性分析方法，取得一定的成果.

涡轮盘常用的材料是粉末合金材料，该材料由粉末冶金工艺生产，常存在缺陷.制造过程中产生的缺陷与传统的铸锻合金的缺陷有所不同[5]，如热诱导孔洞、原始颗粒边界、夹杂物与异金属等，其对疲劳性能具有很大的影响.热诱导孔洞由残留氩气或氦气不溶于合金产生.原始颗粒边界作为裂纹源是由粉末冶金工艺过程产生的，并且在热处理过程中很难消除，严重影响疲劳寿命.夹杂物与异金属严重降低粉末合金的疲劳寿命和力学性能，包括塑性，其中主要有合金中的夹杂物以及粉末中的夹杂物.

传统连续介质力学的研究对象的共同特点是其部件或变形所涉及的尺度较大，常大于若干毫米.近年来连续介质力学开始在其他工程中获得新的应用，例如材料微结构、微电子、微纳米薄膜、微传感器、颗粒或纤维夹杂复合材料微加工等.这些领域应用的共同特点是部件或变形所涉及的特征尺寸很小，约0.1～10.0 μm，即所谓的细观尺度.在细观尺度下，材料的力学性质呈现出很强的尺寸效应，而应变梯度理论是能够很好地解释尺度效应的有效方法之一.常用的商业有限元软件不适合模拟细观尺度下的力学现象，是因为没有考虑特征长度尺度.近年来，研究者通过引进不同长度量纲的参数，提出多种应变梯度理论.[6]

1基于Cosserat理论的弹塑性模型

采用Cosserat模型[7]，其材料点除具有平动自由度ui外，还引入独立的旋转自由度ωi及与其对应的微曲率和偶应力.应变向量ε依赖于位移向量和旋转向量，含有18个应变分量，即εij=uj，i+ejikωk

χij=ωj，i （1）式中：ejik为置换向量；当i=j时χij为扭转微曲率分量，当i≠j时χij为弯曲微曲率分量.合并应变和曲率向量，得到广义应变向量εc=εχT，同样，广义应力向量包含应力和偶应力，即σc=σmT.Cosserat连续体模型平衡方程表达为σji，j+bi=0

mij，i+ejikσik+ψj=0 （2）式中：bi为体力；ψj为体力偶.本构关系表示为σ=Duuε

m=Dωωχ

σc=Dεc （3）弹性刚度阵D=D1000

0D200

00D20

000D20

0D3 （4）其中：D1=λ+2Gλλ

λλ+2Gλ

λλλ+2G （5）

D2=G+GcG-Gc

G-GcG+Gc （6）

D3=4G·diag l2tl2tl2tl2cl2cl2cl2cl2cl2c （7）式中：λ为拉梅常数；G为剪切模量；Gc为Cosserat剪切模量；lt和lc分别为Cosserat材料扭转和弯曲的内部特征长度尺度，可通过实验测定，本文取lt=lc.边界条件可以表示为σijni=j，on Γp

ui=i，on Γu

mijni=j，on Γm

ωi=i，on Γω （8）采用压力无关的von Mises屈服准则模拟不可逆的变形.应力应变关系表示为σ=D：（ε-εp） （9）式中：σ和ε分別为应力和应变张量；εp为塑性应变；D为弹性材料矩阵.塑性流动方程为dεpij=λgσij （10）式中：g为塑性势；σij为流动因子.屈服函数f满足一致性条件f≤0，λ≥0，f·λ=0 （11）2参变量变分原理

采用von Mises屈服准则及关联的流动法则f（σij，εij，p，κ）=σeq-σy（εij，p，κ） （12）式中：κ为材料硬化/软化内变量；σeq为有效应力，表示为σeq=32sijsij1/2

sij=σij-13σkkδij

σm=13σkk （13）σy为屈服应力，对各向同性线性硬化材料，有σy=σ0+ph （14）式中：σ0为初始屈服应力；p为等效塑性应变；h为硬化模量.

对本构关系线性化，屈服函数进行一阶展开得f=f0+fσijdσij+fεij，pdεij，p+fκdκ=

f0+fσijDijkldεkl+-fσijDijklgσkl+

fεij，pgσij+fκhλ（15）利用关系dκ=hλ，引入非负松弛因子v得c1kldεkl+u1λ+w1+v=0，

vλ=0，λ≥0，v≥0 （16）其中： c1kl=fσijDijkl，w1=f0，u1=-fσijDijklgσkl+fεpijgσij+fκh （17）定义势能泛函Π=∫Ω12Dijkldεijdεkl-λDijklgσijdεkldΩ-

∫ΩdbiduidΩ+∫ΓdiduidΓ （18）则参变量变分原理为min Π（dεij，dui，λ）

s.t. c1kldεkl+u1λ+w1+v=0

vλ=0，λ≥0，v≥0 （19）由于 dσkl=Dijkldεij-Dijklλgσij （20）

对泛函变分得δΠ=∫Ωdσijδ（dεij）dΩ-

∫Ωdbiδ（dui）dΩ+∫Γdiδ（dui）dΓ （21）分部积分得δΠ=-∫Ω（dσij，j+dbi）δ（dui）dΩ+

∫Γ（dσijnj-di）δ（dui）dΓ （22）令变分等于0，并考虑δ（dui）的任意性，可得平衡方程和应力边界条件.进一步，由于δ2Π≥0，则泛函取总体最小值.由于泛函是在状态控制方程控制下取极值的，因此整个过程中也满足塑性流动定律.

对方程进行离散，du=Nudu⌒，dε=Bd （21）式中：u为单元内位移向量；u⌒为节点位移向量；Nu为位移插值形函数；B为应变阵.

假定状态方程在单元上积分满足，得U1λ+C1d-d1+v=0

Φ1λ+Kd-dP=0

vλ=0，λ≥0，v≥0 （22）其中：

U1=∫Ω-fσTDgσ+fεpTgσ+fκhdΩ，

CT1=∫ΩBTDfσdΩ，d1=-∫Ω f0dΩ，

Φ1=-∫ΩBTDgσdΩ，K=∫ΩBTDBdΩ，

dP=∫ΩNTudbdΩ+∫ΓNTudpdΓ.

上述线性互补问题可采用自由变量二次规划算法进行求解.[78]

3疲劳寿命分析

3.1假想涡轮盘结构应力分析

假想的涡轮盘结构见图1.材料的弹性模量为200 GPa，泊松比为0.3，密度为7 850 kg/m3，屈服极限为500 MPa，塑性硬化切线模量为10 GPa，Cosserat连续体剪切模量为50 GPa，受到均匀转速所导致的离心力载荷，结构内侧受到约束作用，转速工况为2 100 r/min.

考虑不同尺度参数对弹塑性分析应力结果的影响，尺度参数取为0.05～0.25 m，不同尺度參数的最大von Mises应力见表1.a）涡轮盘结构网格

b）涡轮盘结构约束

Tab.1Maximum von Mises stress of different scale parameters尺度参数/m0.0500.0750.1000.1250.1500.1750.2000.2250.250最大von Mises应力/MPa588.745587.355585.463583.187580.649578.16575.566572.939570.357

由表1可以发现：尺度参数与最大von Mises应力呈近似线性关系，尺度参数越大，最大von Mises应力越小，其中，尺度参数为0.150 m的位移、应力、应变结果分别见图2～4.

4.2疲劳寿命计算

考虑不同尺度参数对疲劳特性的影响，针对特定工况下Cosserat连续体理论弹塑性分析计算出的应力结果计算疲劳寿命.在循环载荷中，考虑完全加载的循环载荷形式.采用基于应力的BrownMiller算法[910]，并采用Goodman平均应力修正公式.

BrownMiller算法认为疲劳损伤是剪应变和正应变的耦合造成的，计算公式为γmax2+εN2=1.65σ′fE（2Nf）b+1.75ε′f（2Nf）c（24）式中：γmax/2为最大剪切应变幅值；εN/2为正应变幅值；σ′f为拉伸疲劳强度系数；E为弹性模量；b为Basquin斜率；ε′f为疲劳韧性系数；c为疲劳韧性指数；Nf为疲劳寿命循环次数.

基于应力的BrownMiller算法的损伤参数用应力表示为τmax2+σN2=E1.65σ′fE（2Nf）b+1.75ε′f（2Nf）c （25） 假设疲劳极限Sf取为500 MPa，Basquin斜率b取为-0.138 3，SN曲线见图5.

同样考虑尺度参数取为0.050～0.250 m，不同尺度参数的临界循环次数见表2.

考虑不同的Basquin斜率对疲劳寿命的影响.疲劳极限Sf取500 MPa，Cosserat连续体尺度参数l取0.150 m，Basquin斜率b取为-0.16～-0.12，不同斜率b的临界循环次数见表3.

表 2不同尺度参数的临界循环次数

Tab.2Critical cycle number under different scale parameters尺度参数/m0.0500.0750.1000.1250.1500.1750.2000.2250.250寿命/（106 次）1.601.641.691.761.851.932.032.132.23

表 3不同斜率b的临界循环次数

Tab.3Critical cycle number of different slope b斜率b-0.16-0.15-0.14-0.13-0.12寿命/（106 次）2.322.111.881.661.43

由表3可以发现：尺度参数越大，寿命越大；b越大，寿命越小.需针对这2个参数讨论概率可靠性问题.

4概率可靠性分析

针对给定载荷工况的假想涡轮盘算例，考虑尺度参数为随机变量，采用二次多项式回归方法，对不同尺度参数得到的寿命数据进行拟合，可以得到拟合后的方程，拟合曲线与原始数据见图6.

考虑安全的循环寿命为1.7×106，则可得到极限状态方程Z，Z>0为安全.Z=N-1.700 0×106=7.168 8×106×l2+

1.076 0×106×l-0.179 2×106 （26）考虑l为随机变量，假设l的均值数学期望值为0.150，标准差为0.033 3，变异因数为0.222.图 6二次多项式拟合曲线与原始数据对比

Fig.6Comparison of quadratic polynomial fitting curve and original data

采用蒙特卡洛方法得到的Z>0的安全概率为93.38%，采用二阶矩的可靠度方法[11]得到的Z>0的安全概率为93.35%，可以发现2种方法相差不大，说明二阶矩的可靠度方法的合理性.

针对给定载荷工况的涡轮盘算例，考虑b为随机变量，采用一次多项式回归方法，尺度参数取0.150 m时的应力结果，对不同斜率b得到的寿命数据进行拟合，可以得到拟合后的方程，拟合曲线与原始数据见图7.

Fig.7Comparison of linear polynomial

fitting curve and original data

考虑安全的循环寿命为1.7×106，则可得到极限状态方程Z，Z>0为安全.Z=N-1.700×106=

-2.230×107×b-2.942×106 （27）考虑b为随机变量，假设b的均值数学期望为-0.140，标准差为0.003 33，变异因数为0.023 8.

采用蒙特卡洛方法得到的Z>0的安全概率为99.24%，采用二阶矩的可靠度方法得到的Z>0的安全概率为99.23%，可以发现2种方法相差不大，说明二阶矩的可靠度方法合理.

同时考虑l和b为随机变量，根据寿命数据，采用二元二次多项式进行回归分析，可以得到拟合后的方程，拟合曲线与原始数据见图8.

考虑安全的循环寿命为1.7×106，则可得到极限状态方程Z，Z>0为安全.

Z=N-1.7×106=

p00-1.7×106+p10l+p01b+p20l2+p11lb（28）

其中，

p00=-1.291×106，p10=-9.839×105，

p01=2.040×107，p20=7.457×106，

p11=1.400×107.

考慮l和b为随机变量，假设l的均值数学期望值为0.150，标准差为0.033 3，变异系数为0.222，假设b的均值数学期望值为-0.140，标准差为0.003 33，变异因数为0.023 8.

采用蒙特卡洛方法得到的Z>0的安全概率为93.25%，采用二阶矩的可靠度方法得到的Z>0的安全概率为93.58%，可以发现2种方法相差不大，但二阶矩方法的计算量要远小于蒙特卡洛方法，说明二阶矩的可靠度方法合理.在实际问题中，需要考虑各种参数对疲劳寿命的敏感性，如果考虑的随机变量不只2个甚至很多，可以采用代理模型的方法[12]构建极限状态方程，并以此模型进行可靠度计算.

6结束语

基于Cosserat连续体理论可以通过尺度参数描述粉末合金的细观微结构的特征，因此建立Cosserat连续体理论的弹塑性模型.采用参变量变分原理构建求解算法，这种算法要比传统的求解算法具有更好的收敛性和稳定性，算例表明材料的尺度参数会影响结构的应力，进而影响结构的疲劳寿命，可以同时考虑材料的不确定性和强度的不确定性来进行疲劳寿命概率可靠性分析.本文将尺度参数和Basquin斜率作为随机变量，并用代理模型和回归分析的方法构建极限状态方程，采用蒙特卡洛方法和二阶矩方法进行可靠度计算，可以说明这种求解策略的合理性.

参考文献：

[1]王应珍， 吕文林. 用摄动法研究几何尺寸为随机量时轮盘的可靠性[J]. 航空动力学报， 1994， 9（4）： 371374.

WANG Y Z， LYU W L. Perturbation technique for reliability analysis of a rotating disk with uncertain geometry[J]. Journal of Aerospace Power， 1994， 9（4）： 371374.

[2]陆山， 吕文林. 轮盘低周疲劳寿命可靠性分析新方法[J]. 航空学报， 1997， 18（2）： 135138.

LU S， LYU W L. New method for reliability analysis of discs LCF life[J]. Acta Aeronautica et Astronautica Sinica， 1997， 18（2）： 135138.

[3]乐晓斌. 用剩余疲劳损伤强度预测机械零件疲劳可靠度及寿命的方法[J]. 机械强度， 1996， 18（1）： 3436.

LE X B. The method for calculating fatigue reliability and life of mechanical parts using residual fatigue damage strength[J]. Journal of Mechanical Strength， 1996， 18（1）： 3436.

[4]高阳， 白广忱， 张瑛莉. 涡轮盘多轴低循环疲劳寿命可靠性分析[J]. 航空学报， 2009， 30（9）： 16781682.

GAO Y， BAI G C， ZHANG Y L. Reliability analysis of multiaxial low cycle fatigue life for turbine disk[J]. Acta Aeronautica et Astronautica Sinica， 2009， 30（9）： 16781682.

[5]张义文， 上官永恒. 粉末高温合金的研究与发展[J]. 粉末冶金工业， 2004， 14（6）： 3043.

ZHANG Y W， SHANGGUAN Y H. Research and development in P/M superalloy[J]. Powder Metallurgy Industry， 2004， 14（6）： 3043.

[6]陈少华， 王自强. 应变梯度理论进展[J]. 力学进展， 2003， 33（2）： 207216.

CHEN S H， WANG Z Q. Advances in strain gradient theory[J]. Advances in Mechanics， 2003， 33（2）： 207216.

[7]张洪武. 参变量变分原理与材料和结构力学分析[M]. 北京： 科学出版社， 2010： 32105.

[8]钟万勰， 张洪武， 吴承伟. 参变量变分原理及其在工程中的应用[M]. 北京： 科学出版社， 1997： 138205.

[9]MILLER K J. Fatigue under complex stress[J]. Metal Science， 1977， 11（89）： 432438. DOI： 10.1179/msc.1977.11.89.432.

[10]BROWN M W， MILLER K J. A theory for fatigue failure under multiaxial stressstrain conditions[J]. Proceedings of Institution of Mechanical Engineers， 1973， 187： 745755. DOI： 10.1243/PIME_PROC_1973_187_069_02.

[11]姚卫星. 结构疲劳寿命分析[M]. 北京： 国防工业出版社， 2003： 187220.

[12]李坚. 代理模型近似技术研究及其在结构可靠度分析中的应用[D]. 上海： 上海交通大学， 2013： 2240.（编辑武晓英）