基于近场动力学方法的水力压裂过程数值模拟

吴凡++李书卉++段庆林++李锡夔++张洪武

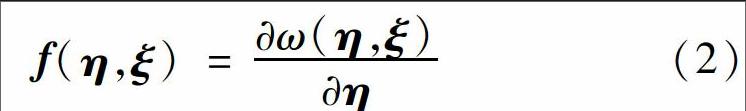
摘要： 利用近场动力学方法便于处理多裂纹萌生、扩展和分叉的优点，将其应用于页岩水力压裂过程的数值模拟.结合页岩水力压裂机理提出在近场动力学中由破坏度跟踪裂纹扩展路径，并通过在新生成裂纹面法线方向施加水压载荷的裂纹追踪方法，成功模拟单射孔横剖面开裂水压实验以及单射孔和多射孔水平井纵剖面的水力压裂过程，得到压裂导致的裂纹缝网结构.数值结果还表明初始射孔裂纹会显著影响后续的水力压裂过程.

关键词： 页岩气开采； 水力压裂； 近场动力学； 裂纹扩展； 多裂纹； 裂纹追踪

中图分类号： TE357.1文献标志码： B

Numerical simulation of hydraulic fracturing process

based on peridynamics method

WU Fan1， LI Shuhui1， DUAN Qinglin1， LI Xikui1， ZHANG Hongwu1

（State Key Laboratory of Structural Analysis for Industrial Equipment，

Dalian University of Technology， Dalian 116024， Liaoning， China）

Abstract： Due to the advantages of peridynamics method in dealing with the initiation， propagation and branching of multiple cracks， it is introduced into the numerical simulation on the hydraulic facture process of shale. Combining with the hydraulic fracture mechanism， a method for tracing crack path according to damage degree in peridynamics is proposed in which the hydraulic pressure is applied in the normal direction of the newly generated crack surface. The cracking pressure of single horizontal well in cross section and the hydraulic fracture of the horizontal well with single and multiple perforations in longitudinal section are successfully simulated by the method. The crack net due to fracturing is obtained. The numerical results also show that the initial perforations have significant effect in the subsequent hydraulic fracture process.

Key words： shale gas extraction； hydraulic fracture； peridynamics； crack propagation； multiple cracks； crack tracking

收稿日期： 2016[KG*9〗09[KG*9〗27修回日期： 2016[KG*9〗11[KG*9〗23

基金项目： 国家自然科学基金（11232003，11372066）；中央高校基本科研业务费专项资金（DUT15LK07）；

遼宁省教育厅重点实验室基础研究项目（LZ2014002）

作者简介： 吴凡（1992—），男，吉林辽源人，博士研究生，研究方向为近场动力学，（Email）251386704@qq.com

通信作者： 李书卉（1979—），女，辽宁沈阳人，博士，工程师，研究方向为材料破坏分析与实验、并行计算技术等，（Email）shuhuili@dlut.edu.cn0引言

页岩气是蕴含在地下深处页岩层区域有机质泥页岩内的气体，是以吸附和游离状态为主的非常规天然气资源.美国对页岩气的开采已有80多年的历史.我国页岩气储量位居世界第一，但开采起步相对较晚.[13]高效的页岩气开采技术对保证能源安全具有重要意义.国家“十二五”和“十三五”规划均对页岩气开采产业进行强有力扶持.

由于页岩埋藏深、质地硬，页岩气被困于页岩体内难以逸出.目前，水力压裂是最有效的页岩气开采技术.该技术将压裂液注入页岩气井中，通过高强度水压压裂岩石进而形成裂缝网络，从而使得页岩气能通过由裂缝形成的高导流通道得以快速析出.

对水力压裂过程实施准确有效的数值模拟有助于深入理解各工艺参数的作用机理，对裂缝形态进行预测，合理配置工艺参数，从而降低生产成本，提高经济效益.然而，由于该过程涉及多裂纹甚至海量裂纹的萌生、扩展和分叉，传统模拟裂纹扩展的数值方法，如扩展有限元法等[45]，难以对其实施有效的数值模拟.

SILLING[6]提出近场动力学模型，其基本方程采用积分形式，因此在连续和不连续处均自然成立，受到力学界的广泛关注[79].由于对裂纹无须进行特殊处理，近场动力学方法十分便于处理多裂纹尤其是海量裂纹的萌生、扩展和分叉问题.因此，该方法十分适合于页岩水力压裂过程的数值模拟，本文将对此进行初步探究.

1近场动力学理论

1.1连续模型

近场动力学基本方程基于牛顿第二定律的积分形式描述物质点运动.假设结构内任一物质点与其一定范围内的其他物质点具有一定的相互作用，其基本方程为ρu··（x，t）=∫Hf（u（x^，t）-u（x，t），x^-x）dx^+

b（x，t） （1）式中：ρ，u和 b分别为密度、位移和外力体力项；f为力密度函数，被称作对点力函数，代表物质点x^对其临近的物质点x的作用；H为影响域，与无网格法的影响域定义相似，用于描述该物质点x所能作用的其他物质点所涵盖的区域.

可视近场动力学为一种宏观的分子动力学[10]，两物质点间的相互作用f可比拟为分子动力学中原子之间的范德华力，称为键.对点力函数包含物质本构的所有信息，包括线性以及非线性等，因此通过修改对点力函数，对弹性、塑性、非线性问题均可以适用.对于微弹性材料，其对点力函数能够由一个标量的微势能函数的微分得到，即f（η，ξ）=ω（η，ξ）η （2）式中：ω（η，ξ）为微势能函数，其物理意义为单个键内储存的能量，ξ=x^-x和η=u^-u分别为参考位置向量和相对位移向量.对于微弹性材料，有ω（η，ξ）=c（ξ）s2ξ2 （3）式中：ξ=ξ；η=η；s为键伸长，类似于应变，代表键的伸长比率.s定义为s=（ζ-ξ）/ξ （4） 式中：ζ=ξ+η为当前构型下的相对位置向量，模量ζ=ξ+η代表当前键长.微模量c（ξ）表征材料刚度，物理意义为微观下键的刚度.对于微弹性材料，c（ξ）与ξ无关.在各项均匀拉伸变形下，将两者应变能密度等效，可得出微模量与经典力学中物理量的关系[6]为c=6Eπδ4（1-2ν） （5）式中：E为弹性模量；ν为泊松比；δ为影响域半径.对于二维平面应力有c=9Eπδ3（1-2ν） （6）1.2断裂模型

由动量守恒定律可知f平行于ζ，因此微弹性材料对点力函数可写为f=ξ+ηξ+ηcsμ=ξ+ηξ+ηf （7）式中：f为对点力函数f的模量.因此，f=csμ （8）式中：μ为01函数，用以引入断裂，表示该键的断裂或完好，μ=1，s

0，其他 （9）式中：s0为极限伸长率，代表引发键断裂的最大键伸长，当达到该设定值时，该键断裂.微观下键的断裂在宏观上能够反映裂纹的发展情况.为在宏观上描述断裂，定义破坏度φ用以表示物质点断裂情况，φ（x，t）=1-∫H μ（x，t，ξ）dVH∫HdVH （10）式中：φ=0代表与该物质点相连的所有键都保持完好，φ=1代表该点游离于结构.

2水力压裂的近场动力学模型

水力压裂过程示意见图1.通过从地表钻入竖井，穿过地下水层，深入到地下页岩区域，然后换钻头打大斜度的水平井.水平井完成以后，通过送入井内的射孔枪进行井内射孔.射孔弹穿过井壁打入岩层，从而连通井内和岩区形成通道.由于射孔弹穿透效果有限，需要在射孔之后进行水力压裂.通过地面的压裂车的高压泵组将压裂液注入水平井内，利用高强度水压压裂页岩储层基质形成复杂裂纹网络，使裂缝壁面与储层基质的接触面积更大，缩小油气从任意方向的基质向裂缝输出的渗流距离，为页岩气形成高导流通道，加快页岩气的析出.[2]

Fig.1Schematic of hydraulic fracture process

水力压裂是页岩气开采的主要增产措施，压裂的体积改造是目前研究的热点，即进一步提高储层总剖面的使用程度，追求裂纹数目更多、裂纹形态更复杂、延伸距离更远的缝网压裂技术.因此，本文针对水平井的横纵剖面分别进行二维近场动力学数值模拟，对缝网的形成机制进行机理探究.

页岩岩体物理参数取自吉林省农安油田的页岩实验数据，见表1.近场动力学二维微弹性模拟的泊松比固定为1/3[10]，且由于泊松比对裂纹路径、分叉的影响很小[11]，所以计算泊松比也取1/3.

Tab.1Parameters of shale materialE/GPaρ/（kg/m3）νs01.9032 4001/30.009 148 7

时间积分格式采用VelocityVerlet算法，射孔初始裂纹采用预先在结构内添设的方式实现.为施加水压，须对裂纹进行追踪.为简便起见，在本文的实现中，破坏度为0.35<φtrace<0.50的粒子被认为处于裂纹面上，而水压的施加方向为断裂键的“平均”方向.这里的“平均”是指对各断裂键的取向根据其键长进行加权平均，其中权重系数αb（ξ）的计算式为αb（ξ）=∞i=1piξΔxi-1（11）式中：pi为拟合的多项式系数.对于本文采用的均匀节点分布，在离散δ=3时权重系数αb（ξ）的取值见表2.

Tab.2Fitting points for directional weight coefficientsξ/Δx1223αb（ξ）1.001.000.300.01

3数值算例

通过几个数值算例考察建立的近场动力学方法模拟水力压裂过程的效果.為验证近场动力学模型对裂纹扩展模拟的有效性和准确性，算例1模拟KalthoffWinkler实验，算例2考察初始裂纹对所需压裂水压的影响情况，算例3考察单射孔水平井纵剖面的水力压裂裂纹扩展情况，算例4进行多射孔水平井纵剖面的模拟.

3.1KalthoffWinkler实验

KalthoffWinkler实验是研究断裂扩展角度的著名实验.实验中测得裂纹扩展角度呈70°.现采取的结构尺寸见图2.其中，v0=20 m/s.近场动力学模拟结果见图3.

Fig.2KalthoffWinkler experiment setup

Fig.3KalthoffWinkler experiment simulation result obtained by peridynamics method

模拟得到的裂纹扩展角度与实验测得的角度非常接近.裂纹在扩展一段距离之后便不再扩展（由于整体运动的产生），这一点与实验结果也吻合.这些数值结果表明近场动力学方法能够准确有效地模拟裂纹的扩展过程.

3.2初始裂纹对压裂水压的影响

该算例考虑水平井的横剖面，分为有初始裂纹的套管井和无初始裂纹的裸眼井.水平井横剖面示意图和水压加载见图4.结构尺寸为10.00 m×10.00 m，均匀离散下网格尺寸为Δx=0.02 m，节点数为65 000个，中央处水平井直径为0.60 m，其中，套管井的射孔长度为0.60 m，裸眼井无射孔，对比2种井各自所需的起裂水压.水压加载见图4b，增量为1 MPa/ms，0.200 ms后恒定（足够大）.2种井的压裂效果云图见图5.由此可看出：裸眼井的破裂压力为13.2 MPa，而套管井的射孔在5.8 MPa时开始发生裂纹扩展，0.250 ms时发生分叉.该结果显示射孔套管井能够显著降低所需的起裂水压.

a）整体示意b）裸眼井与套管井示意c）水压加载

Fig.4Schematic of cross section of horizontal

well and hydraulic loading

a）裸眼井b）套管井

Fig.5Crack propagation process of horizontal wells

3.3单射孔水平井纵剖面压裂过程模拟

带有射孔的套管水平井的纵剖面见图6.追踪裂纹扩展，持续施加水压以观测水力压裂裂纹扩展效果.结构尺寸为20.0 m×20.0 m，射孔深度a=1.0 m，网格尺寸为Δx=0.1 m.结构最外层设定为非破坏区，即s0→∞.加载水压p从0开始，到t=50 ms为pmax=24 MPa，时间步长Δt=10-5s.

Fig.6Longitudinal section of horizontal well with single perforation and its hydraulic loading curves

单射孔纵剖面水平井水力压裂过程见图7.由图7可知：射孔裂纹在裂纹扩展后发生裂纹分叉以及多级分叉现象，表明近场动力学方法可以十分方便且有效地模拟裂纹扩展和分叉问题.a）t=0.40 msb）t=0.55 msc）t=0.65 msd）t=70 mse）t=80 msf）t=85 ms图 7单射孔纵剖面水平井水力压裂过程

Fig.7Hydraulic fracture process of longitudinal section of horizontal well with single perforation

3.4多射孔水平井纵剖面压裂过程模拟

水平井在射孔作业时往往需在套管井井筒内壁上射多个孔眼以进行压裂.该算例考察多射孔水平井的情况.采用40.0 m×20.0 m结构，3射孔同时压裂.射孔长度a=1.0 m，射孔间距b=5.0 m，见图8.网格尺寸Δx=0.1 m，时间步长Δt=10-5s.非破坏区域与水压加载方式同前例.

图 8多射孔水平井纵剖面示意

Fig.8Schematic of longitudinal section of horizontal

well with multiple perforations

模拟得到的裂纹扩展过程见图9.一个显著的特点是在两侧裂纹发生明显扩展后，中央裂纹才开始缓慢扩展，并且直到最后；相比于两侧裂纹，中央裂纹的扩展和分叉也很小，表现为两侧裂纹对中央裂纹具有一定的抑制作用.这表明由于裂纹间的相互影响，多裂纹的扩展过程更为复杂，与单裂纹的扩展过程具有明显的差异.该算例的模拟结果对实际工程具有一定的指导意义，表明高密度的初始裂纹分布并不能得到高密度的裂缝网络.因而，工程上应合理安排射孔排布，以减少成本并达到更好的压裂效果.

a）t=50 msb）t=70 msc）t=80 msd）t=100 ms图 9多射孔纵剖面水平井水力压裂过程模拟结果

Fig.9Simulation results of hydraulic fracture process in longitudinal section of horizontal well with multiple perforations

4结束语

利用近场动力学方法便于模拟裂纹萌生、扩展和分叉的显著优点，发展页岩水力压裂过程的数值模拟方法.模拟结果表明该方法不仅能模拟页岩的水力压裂过程、预测最终的裂缝网络拓扑，而且能定性揭示该工艺过程的一些力学机理，如：初始射孔能显著降低起裂水压，由于裂纹间的相互影响须合理安排射孔间距等.当然，本文工作仅是定性意义上的二维模拟，对于工程亟需的定量的三維模拟仍需深入研究.参考文献：

[1]OUCHI H， KATIYAR A， YORK J， et al. A fully coupled porous flow and geomechanics model for fluid driven cracks： a peridynamics approach[J]. Computational Mechanics， 2015， 55（3）： 561576. DOI： 10.1007/s0046601511238.

[2]朱海燕， 赵军， 邓金根， 等. 水力压裂过程中微环隙的产生和扩展的数值模拟[J]. 计算机辅助工程， 2013， 22（S2）： 443447. DOI： 10.3969/j.issn.10060871.2013.z2.108.

ZHU H Y， ZHAO J， DENG J G， et al. Numerical simulation on microannulus initiation and propagation during hydraulic fracturing[J]. Computer Aided Engineering， 2013， 22（S2）：443447. DOI： 10.3969/j.issn.10060871.2013.z2.108.

[3]董大忠， 邹才能， 杨桦， 等. 中国页岩气勘探开发进展与发展前景[J]. 石油学报， 2012， 33（S1）： 107114.

DONG D Z， ZOU C N， YANG H， et al. Progress and prospects of shale gas exploration and development in China[J]. Acta Petrolei Sinica， 2012， 33（S1）： 107114.

[4]BELYTSCHKO T， BLACK T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering， 1999， 45（5）： 601620. DOI： 10.1002/（SICI）10970207（19990620）45：5<601：：AIDNME598>3.0.CO；2S.

[5]MOE··S N， DOLBOW J， BELYTSCHKO T. A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering， 1999， 46（1）： 131150. DOI： 10.1002/（SICI）10970207（19990910）46：1<131：：AIDNME726>3.0.CO；2J.

[6]SILLING S A. Reformulation of elasticity theory for discontinuities and longrange forces[J]. Journal of the Mechanics and Physics of Solids， 2000， 48（1）： 175209. DOI： 10.1016/S00225096（99）000290.

[7]HU W， HA Y D， BORARU F. Peridynamic model for dynamic fracture in unidirectional fiberreinforced composites[J]. Computer Methods in Applied Mechanics and Engineering， 2012， 217220： 247261. DOI： 10.1016/j.cma.2012.01.016.

[8]REN H， ZHUANG X， CAI Y， et al. Dualhorizon peridynamics[J]. International Journal for Numerical Methods in Engineering， 2015， 108（12）： 125. DOI： 10.1002/nme.5257.

[9]BESSA M A， FOSTER J T， BELYTSCHKO T， et al. A meshfree unification： reproducing kernel peridynamics[J]. Computational Mechanics， 2014， 53（6）：12511264. DOI： 10.1007/s004660130969x.

[10]SILLING S A， ASKARI E. A meshfree method based on the peridynamic model of solid mechanics[J]. Computers & Structures， 2005， 83（17）： 15261535. DOI： 10.1016/j.compstruc.2004.11.026.

[11]HA Y D， BORARU F. Studies of dynamic crack propagation and crack branching with peridynamics[J]. International Journal of Fracture， 2010， 162（1）： 229244. DOI： 10.1007/s1070401094424.

[12]SONG J H， AREIAS P M， BELYTSCHKO T， et al. A method for dynamic crack and shear band propagation with phantom nodes[J]. International Journal for Numerical Methods in Engineering， 2006， 67（6）： 868893. DOI： 10.1002/nme.1652.（編辑武晓英）第26卷 第1期2017年2月计 算 机 辅 助 工 程Computer Aided EngineeringVol.26 No.1Feb. 2017