浅谈如何上好整理复习课

胡长玲

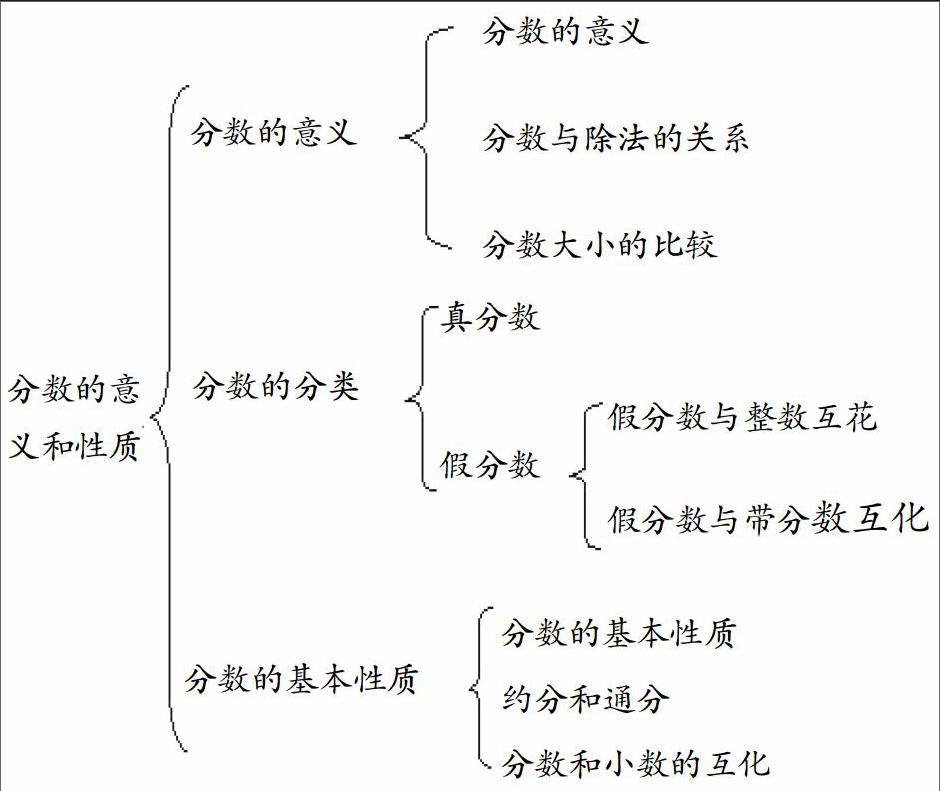
整理复习课在数学课堂教学中非常重要，是小学数学一种基本课型，它不同于新授课和练习课。它承载着“回顾与整理，沟通与生长”的独特功能，是把学生所学知识进一步系统化的过程。新课程下，复习课的主要针对某一阶段所学知识进行整理归纳，使知识条理化，系统化，查缺补漏，进一步巩固深化知识。使学生认识到知识的相关联系，把知识形成链条形成网络，形成知识网，使书越学越薄，提高学生总结知识的能力，做好这一阶段的反思，完善认知系统，发展数学能力，促进学生全面发展。

一、注重知识梳理，梳理知识，融会贯通

复习课的重要功能就是引导学生按一定的标准进行梳理归类。当然，其实在每一节的新授课和练习课时也应该做好知识的前后联系，这样才能在复习课中梳理知识时容易很多。例如在做分数的认识和分数与除法这一复习课时，我采用现在黑板上写出分数4/5，让学生说出，看到五分之四这个分数你能想到什么？有的学生会想到它的分数单位是1/5，还会想到他是把单位“1”平均分成5份，取其中的4份，也就是分数的意义。还有的学生会想到这个分数表示4÷5。老师因势利导，划出一条直线，能否在这直线上表示出4/5呢？有的说能，有的说不能，争论后得出结论：必须先在直线上标出一条线段作为单位“1”，然后才能把这个单位“1”平均分成五份，取其中的4份。再一次强调单位“1”与平均分的重要性。在复习分数这一章时，可以与学生一起梳理出知识脉络。

例如在复习多边形面积时，先把基础知识夯实，把知识点、图形的特征、基本公式、基本练习明确后，让学生认识到构造这种网络学习的好处。在复习时更要关注公式的推导过程，不能让学生死记公式，渗透数学思想方法，让复习过程成为一个动态提升的过程。例如在复习三角形，平行四边形，梯形面积时，先一起找出三者面积公式之间的联系与区别，发现其实最后都可以统一成梯形的面积公式（上底+下底）×高÷2来表示，只不过三角形的上底为0，在平行四边形里上底和下底相等，上底+下底=2×下底，是学生充分认识到知识之間的融会贯通，找到知识间的联系与区别。

二、典型变式习题，在变中求联

练习设计要精选有代表性的习题，要注重习题的综合性和代表性。例如在复习分数的认识这节课时先画出一个图形，

让学生说出你能写出哪些分数？

学生都能写出1/4，3/4这样的分数。把整个椭圆看成单位“1”，白色部分占整个圆的3/4，红色部分占整个圆的1/4。老师再抛出问题，还能写出其他的分数吗？给学生思考和讨论的时间，有个别学生会想到1/3这个分数，红色部分占白色部分的1/3，白色部分是红色部分的3倍，又一次巩固了单位“1”不同，写出的分数也不同。在复习多边形面积这一课时，可以和学生一起准备七巧板，在七巧板的不断变化过程中整理出所学知识，学生兴趣盎然。

三、复习课要注重查缺补漏

对于容易混淆的知识点，平时训练时哪些知识点掌握的不好，老师一定要心中有数，在复习课上再次复现，加深理解。概念梳理后，为了更好地查缺补漏，设计一些综合类习题，提高学生能力。例如整理因数与倍数这一章时，重点概念可以以题为载体，设计了以下学生易错习题，更好地查缺补漏。

（1）最小的奇数是（ ），最小的偶数是（ ），最小的质数是（ ），最小的合数是（ ）。

（2）12的所有因数有（ ），50以内5的倍数（ ）。

（3）18的最大因数是（ ），18的最小倍数是（ ）。

（4）在6×8=48中，（ ）是6的倍数，（ ）和（ ）是30的因数。

（5）在7，9，12，15，43，59，99中，奇数有（ ），偶数有（ ），质数有（ ），合数有（ ）。

概念性较多的章节中，用典型习题的方式查缺补漏，效果很好。其实，数学知识就像一粒粒宝贵的珍珠，只有把它们串起来才更有价值，从整理复习课中，关键要让学生养成自觉及时地把学过的知识进行归纳整理，是所学知识形成网络，提高学习能力。