一个两类矩阵乘积特征值实部的估计

沈 浮,夏必腊,李文涛

(中国人民解放军陆军军官学院 数学教研室，合肥 230031)

一个两类矩阵乘积特征值实部的估计

沈 浮,夏必腊,李文涛

(中国人民解放军陆军军官学院 数学教研室，合肥 230031)

在证明了复正规矩阵特征值实部具有单调性的基础上，给出了Hermite矩阵与复正规矩阵乘积特征值实部的范围，具有一定的理论价值和应用价值。

Hermite矩阵；复正规矩阵；复正定矩阵；正交补空间；可交换

本文用A>0(A≥0)表示A为正定(半正定)的Hermite矩阵；用A>B(A≥B)表示A-B是复正定(半正定)矩阵；用Re(z)表示复数z的实部；用λ(A)表示矩阵A的特征值；Hermite矩阵A的n个特征值按如下排列：λ1(A)≤λ2(A)≤…≤λn(A)；用λRmin(A)和λRmax(A)分别表示复矩阵A实部最小的特征值和实部最大的特征值。

文献[1]的定理4.4.1指出：A、B为2个Hermite矩阵，若A≥B，则λi(A)≥λi(B)(i=1,2,…,n)。本文把这一结果推广到A、B为复正规矩阵的情形，并利用它估计出了Hermite矩阵与复正规矩阵乘积特征值实部的范围，得到了一些有价值的结果。

1 相关定义及引理

定义1 设A∈Cn×n，若对任意的非零列向量x∈Cn都有Re(xHAx)>0(或Re(xHAx)≥0)，则称A为复正定矩阵(或复半正定矩阵)；若对任意的非零列向量x∈Cn都有Re(xHAx)<0，则称A为复负定矩阵。

显然A>0(A≥0)，它也是复正定(半正定)矩阵。

引理1[2]设A∈Cn×n，A>0(A≥0)，则存在唯一的正定(半正定)矩阵G满足A=G2，且任一个与A可交换的矩阵B必和G可交换。

引理2[3]设A∈Cn×n是复矩阵，且A为正规矩阵，则λRmin(A)E≤A≤λRmax(A)E(其中E为n阶单位矩阵)。

定义2 设A∈Cn×n是复正规矩阵，对任意非零列向量x∈Cn，称复数

(1)

为复正规矩阵A的Rayleigh商。

引理3[4]设A∈Cn×n是复正规矩阵，其n个特征值λ1=a1+ib1，λ2=a2+ib2，…，λn=an+ibn满足a1≤a2≤…≤an，相应的标准正交特征向量依次是x1，x2，…，xn。

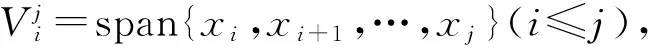
引理4 设A∈Cn×n是复正规矩阵，其n个特征值λ1=a1+ib1，λ2=a2+ib2，…，λn=an+ibn满足a1≤a2≤…≤an，k是给定的整数(1≤k≤n)，Vk是n维复向量空间中任意k维子空间，则有

(2)

证明 设A∈Cn×n的属于特征值λ1,λ2,…,λn的标准正交特征向量依次是x1，x2，…，xn，用Rk表示k-1 维子空间span{x1,x2,…,xk-1}的正交补空间，它是n-k+1维的。因此，Vk与Rk必有公共的非零向量yk，故由引理3的 1)得

(3)

又yk∈Vk，故

(4)

因此

(5)

又由引理3的 2)知

(6)

故

(7)

引理5[1]设A≥0，k是实数，A和kA的特征值排列如下：λ1(A)≤λ2(A)≤…≤λn(A)，λ1(kA)≤λ2(kA)≤…≤λn(kA)。则(1)k≥0时，λi(kA)=kλi(A)，i=1,2,…,n；(2)k<0时，λi(kA)=kλn-i+1(A)，i=1,2,…,n。

2 主要结果

定理1和定理2就是本文的主要结果。

定理1 设A、B是n阶复正规矩阵，Re(λ1(A))≤Re(λ2(A))≤…≤Re(λn(A))，Re(λ1(B))≤Re(λ2(B))≤…≤Re(λn(B))，若A≥B，则Re(λk(A))≥Re(λk(B))，(k=1,2,…,n)。

证明 因A≥B，所以对任取的非零列向量x∈Cn×1有：Re(xHAx)≥Re(xHBx)。设Vk是n维复向量空间中任意k维子空间，则有

(8)

从而有

(9)

故由定理4知

Re(λk(A))≥Re(λk(B))，k=1,2,…,n

(10)

定理2 设A∈Cn×n是半正定的Hermite矩阵，B∈Cn×n是复正规矩阵，AB=BA，则：

1) 若B是复半正定的，有

Re[λRmin(B)]·λi(A)≤Reλi(AB)≤Re[λRmax(B)]·λi(A)，i=1,2,…,n

(11)

2) 若Re[λRmax(B)]≥0，Re[λRmin(B)]≤0，有

Re[λRmin(B)]·λn-i+1(A)≤Reλi(AB)≤Re[λRmax(B)]·λi(A)，i=1,2,…,n

(12)

3) 若B是复负定矩阵，有

Re[λRmin(B)]·λn-i+1(A)≤Reλi(AB)≤Re[λRmax(B)]·λn-i+1(A)，i=1,2,…,n

证明 由引理2知λRmin(B)E≤B≤λRmax(B)E，于是

λRmax(B)A=A1/2[λRmax(B)E-B]A1/2+A1/2BA1/2≥A1/2BA1/2

(13)

A1/2BA1/2=A1/2[B-λRmin(B)E]A1/2+λRmin(B)A≥λRmin(B)A

(14)

所以

λRmin(B)A≤A1/2BA1/2≤λRmax(B)A

(15)

因AB=BA，所以ABH=BHA，即A与BH也可交换。由引理1知

(A1/2BA1/2)(A1/2BA1/2)H=A1/2BA1/2A1/2BHA1/2=A1/2BHA1/2A1/2BA1/2=

(A1/2BA1/2)H(A1/2BA1/2)

(16)

即A1/2BA1/2为复正规矩阵。从而根据定理1得

Reλi[λRmin(B)A]≤Reλi(A1/2BA1/2)≤Reλi[λRmax(B)A]

(17)

1) 当B是复半正定时，Reλi(B)≥0，又A≥0，即λi(A)≥0，于是由式(17)及引理5可得

Re[λRmin(B)]·λi(A)≤Reλi(A1/2BA1/2)≤Re[λRmax(B)]·λi(A)

(18)

即

Re[λRmin(B)]·λi(A)≤Reλi(AB)≤Re[λRmax(B)]·λi(A)，i=1,2,…,n

(19)

2) 当Re[λRmax(B)]>0，Re[λRmin(B)]<0时，由引理5知

Reλi[λRmin(B)A]=Re[λRmin(B)]·λn-i+1(A)

(20)

于是得

Re[λRmin(B)]·λn-i+1(A)≤Reλi(A1/2BA1/2)≤Re[λRmax(B)]·λi(A)

(21)

即

Re[λRmin(B)]·λn-i+1(A)≤Reλi(AB)≤Re[λRmax(B)]·λi(A)，i=1,2,…,n

(22)

3) 若B是复负定矩阵，由文献[4]的定理5证明过程知：B的特征值实部均小于0，从而Re[λRmin(B)]<0，Re[λRmax(B)]<0，于是有

Re[λRmin(B)]·λn-i+1(A)≤Reλi(A1/2BA1/2)≤Re[λRmax(B)]·λn-i+1(A)

(23)

即

Re[λRmin(B)]·λn-i+1(A)≤Reλi(AB)≤Re[λRmax(B)]·λn-i+1(A)，i=1,2,…,n

(24)

[1] 王松桂，吴密霞，贾忠贞．矩阵不等式[M]．2版.北京：科学出版社，2006：79-88，96-99．

WANG Songgui,WU Mixia,J IA Zhongzhen.Matrix Inequality[M].2thEdition.Beijing:Science Press,2006:79-88,96-99.

[2] 史荣昌，魏丰．矩阵分析[M]．3版.北京：北京理工大学出版社，2010：134-139，144-147．

SHI Rongchang,WEI Feng.Matrix Analysis[M].Beijing:Beijing Institute of Technology Press,2010：134-139，144-147．

[3] 沈浮，夏必腊，周堂春．关于复正规矩阵的两个不等式[J]．江西科学，2014，32(1)：5-7．

SHEN Fu,XIA Bila,ZHOU Tangchun.Two Inequalities on Complex Normal Matrix[J].Jiangxi Science,2014,32(1):5-7.

[4] 沈浮，王鹏．复正规矩阵特征值实部的表示[J]．陆军军官学院学报，2013，33(144)：101-102．

SHEN Fu,WANG Peng.Representation of the real part of eigenvalues of complex normal matrix[J].Journal of Army Military Academy,2013,33(144):101-102.

[5] 郭安学．正定复矩阵的几个性质[J]．山西师范大学学报(自然科学版)，2003，17(2)：18-19．

GUO Anxue.Some Properties of Positive Definite Complex Matrix[J].Journal of Shanxi Teachers University(Natural Science Edition),2003，17(2)：18-19．

[6] 方保镕，周继东，李医民．矩阵论[M]．北京：清华大学出版社，2004：109-117．

FANG Baorong,ZHOU Jidong,LI Yimin.Matrix Theory[M].Beijing:Tsinghua University Press，2004：109-117．

[7] 程云鹏，张凯院，徐仲．矩阵论[M]． 3版.西安：西北工业大学出版社，2006：365-371．

CHENG Yunpeng,ZHANG Kaiyuan,XU Zhong.Matrix Theory[M].3thEdition.Xi’an:Northwestern Polytechnical University Press:2006：365-371．

[8] 袁晖坪．关于复矩阵乘积的正定性[J]．数学的实践与认识，2006，36(11)：202-206．

YUAN Huiping.On Metapositive Difinite of Product of Complex Matrices[J].Mathematics in Practice and Theory,2006，36(11)：202-206．

[9] 詹兴致．矩阵论[M]．北京：高等教育出版社，2008：39-45．

ZHAN Xingzhi.矩阵论[M].Beijing:Higher Education Press,2008:39-45.

(责任编辑 刘 舸)

An Estimate of Eigenvalue Real Part of the Product of Two Kinds of Matrices

SHEN Fu, XIA Bi-la, LI Wen-tao

(Teaching and Research Section of Mathematics，PLA Army Officer Academy, Hefei 230031, China)

This paper firstly proved the monotonicity of the eigenvalue real part of complex normal matrices and then gave the range of the eigenvalue real part of the product of Hermite matrix and complex normal matrix. The content of the paper has some theoretical and practical values.

Hermite matrix； complex normal matrix；complex positive definite matrix；orthogonal complement space； convertible

2016-07-16 基金项目：安徽省自然科学基金资助项目(1408085MA06)

沈浮(1959—)，男，副教授，主要从事大学数学教学和矩阵理论方面的研究，E-mail:pbxysf@126.com。

沈浮,夏必腊,李文涛.一个两类矩阵乘积特征值实部的估计[J].重庆理工大学学报(自然科学)，2017(2):153-156.

format：SHEN Fu, XIA Bi-la, LI Wen-tao.An Estimate of Eigenvalue Real Part of the Product of Two Kinds of Matrices[J].Journal of Chongqing University of Technology(Natural Science)，2017(2):153-156.

10.3969/j.issn.1674-8425(z).2017.02.025

O151

A

1674-8425(2017)02-0153-04