格栅套筒加筋碎石桩复合地基沉降计算方法

贺成斌,赵明华,马缤辉,陈秋南,雷 勇

(1.湖南大学土木工程学院,湖南 长沙 410082; 2.湖南科技大学土木工程学院,湖南 湘潭 411201)

格栅套筒加筋碎石桩复合地基沉降计算方法

贺成斌1,2,赵明华1,马缤辉2,陈秋南2,雷 勇2

(1.湖南大学土木工程学院,湖南 长沙 410082; 2.湖南科技大学土木工程学院,湖南 湘潭 411201)

为研究格栅套筒加筋碎石桩复合地基的变形特性及沉降计算方法,开展加筋碎石桩复合地基承载变形机理分析。将复合地基划分为加筋段、非加筋段和下卧层三部分:基于空间问题的胡克定律和分层总和法思路,考虑加筋段桩土存在相对滑移但不出现塑性区,采用桩体单元并利用分层迭代法予以计算;由于非加筋段桩土竖向和径向变形协调,引入桩土单元体模型予以分析;下卧层沉降量则通过分层总和法计算,从而推导出格栅套筒加筋碎石桩复合地基沉降计算公式。工程实例分析结果表明,上述沉降计算方法所得结果与实测值较接近,且克服了现有分析方法所得结果偏于危险的缺陷,具有较好的合理性与可行性。

格栅套筒;加筋碎石桩;沉降计算;竖向变形;径向变形;桩土相对滑移

碎石桩作为一种常见的地基加固形式已广泛应用于软土地基加固工程中[1-2]。碎石桩的承载力主要取决于桩周土提供的侧向约束力。当桩周土提供的侧向约束力不足时,碎石桩桩身上半段易发生鼓胀变形,致使其承载力降低、沉降增大而无法达到预期的地基加固效果[3]。为此,工程中采用在2～3倍桩径深度范围内对碎石桩包裹土工格栅套筒的处理方法,利用格栅套筒对桩体的围箍作用,增大其侧向约束力,限制桩体鼓胀变形,从而达到提高承载力和减小沉降的目的。这一新型复合地基可称之为“格栅套筒加筋碎石桩复合地基”。由于格栅套筒的围箍作用,碎石桩承载和变形特征均发生变化,此时简单地套用已有的碎石桩复合地基沉降计算方法进行沉降分析不合时宜。因此,如何结合格栅套筒加筋碎石桩的特点,深入探讨加筋碎石桩复合地基沉降计算方法,对工程设计具有重要的理论指导意义。

目前,加筋碎石桩复合地基的研究手段多为室内试验、数值模拟和现场测试等,研究多集中于承载力、稳定性分析方面,如周志刚等[4]较早就利用极限平衡理论对土工格栅套筒加筋碎石桩进行了承载力分析;陈昌富等[5-7]分别基于圆孔扩张理论、滑块平衡法和极限分析上限法推导了顶部加筋碎石桩承载力计算公式;赵明华等[8-9]基于极限平衡理论进一步考虑土工格栅套筒加筋碎石桩的破坏模式，推导得出加筋碎石桩单桩极限承载力计算公式。然而，加筋碎石桩复合地基沉降计算方面的研究相对偏少，曹文贵等[10]根据桩与桩周土相对滑移量的不同,将加筋碎石桩分为加筋区、非加筋塑性区和非加筋弹性区,并根据不同区段的变形特点分别建立相应的沉降分析模型,从而得到柔性基础下加筋碎石桩复合地基沉降计算方法;吴梦婷等[11]同样将加固区分为3个区段,基于弹性力学及桩土协调变形推导出各区段沉降计算式。虽然上述理论研究都对加筋碎石桩承载变形机理进行了分析,但仍具有一定的局限性和不足,如对碎石桩加筋段桩土相对滑移导致的桩侧摩阻力考虑得过于复杂；桩体受荷后桩体侧向变形随深度衰减很快,不一定存在塑性区,从而使得分区假设不一定成立;从计算结果来看,理论分析值小于实测值,计算偏于危险。因此,本文拟在前人研究基础上,将格栅套筒加筋碎石桩复合地基分为加筋段、非加筋段和下卧层三部分,并基于空间问题的胡克定律和分层总和法思路,考虑加筋段桩土存在相对滑移但不出现塑性区,采用桩体单元并利用分层迭代法予以计算;由于非加筋段桩土竖向和径向变形协调,引入桩土单元体模型予以分析;下卧层沉降量则通过分层总和法计算,从而提出格栅套筒加筋碎石桩复合地基沉降计算方法。

图1 格栅套筒加筋碎石桩复合地基组成

1 格栅套筒加筋碎石桩复合地基变形机理

一般而言,格栅套筒加筋碎石桩复合地基由垫层、加固区和下卧层组成[1](图1)。由于垫层的厚度较小、压实度较高,沉降变形在施工阶段就基本完成,因而可以忽略垫层的沉降。故加筋碎石桩复合地基沉降S可看作加固区压缩变形量S1与下卧层压缩变形量S2之和:

S=S1+S2

(1)

根据已有研究成果[9-11],加固区根据桩体是否被土工格栅套筒包裹可分为加筋段与非加筋段,故S1可表示为

S=S11+S12

(2)

式中：S11、S12分别为加筋段和非加筋段压缩变形量。

由式(1)(2)可得

S=S11+S12+S2

(3)

式(3)即为目前较为常用的加筋碎石桩复合地基沉降计算方法,其中下卧层压缩变形量S2采用传统的分层总和法求解。由此可以看出,加筋碎石桩复合地基沉降计算的关键在于加固区压缩变形量S11和S12的确定。

1.1 加筋段

由于桩体受到格栅套筒的包裹作用,加筋段的整体性及变形刚度大幅度提高,并借助于格栅形成较为清晰的桩土接触面,其变形机理与柔性桩或半刚性桩类似。但桩体由散体材料构成，本身无黏聚力,在荷载作用下桩体应力集中产生不可忽略的鼓胀变形。当复合地基承受荷载较大时,加筋段桩土界面存在相对位移或位移趋势,导致桩土界面存在桩侧摩阻力。因此,加筋段压缩变形计算需考虑桩土竖向变形、径向变形和桩侧摩阻力的影响。本文分析加筋段沉降量时,采用桩体单元并利用分层迭代法予以计算。

1.2 非加筋段

由于桩体未受到格栅套筒的侧向约束,非加筋段的桩体刚度明显下降,在荷载作用下非加筋段桩体存在竖向和径向变形,特别是加筋段与非加筋段交界处桩体刚度突变,桩身径向变形会异常明显,这也是加筋碎石桩可能发生鼓胀破坏的原因[12-13]。由于无格栅套筒,碎石桩体与桩周土体相互嵌入咬合,桩土界面界限非常模糊,桩土相对位移很小,可忽略不计,又因应力扩散作用桩体受所附加应力随深度急剧减小，其侧向变形相应减小,因此整个非加筋段鼓胀变形不均匀,但考虑桩土变形连续且协调特点,为简化计算,非加筋段采用桩土单元体进行分析。

由此可知,本文建立的加筋碎石桩复合地基沉降分析方法必须充分反映上述加筋段与非加筋段的变形力学机理。为此,下面将在此基础上分别对加筋段和非加筋段沉降变形进行分析。

2 加固区压缩变形分析

2.1 基本假定

本文研究主要针对采用双向高强土工格栅在碎石桩顶部以下2～3倍桩径深度范围内套筒围箍所形成的加筋碎石桩,为简化计算,作如下基本假定:①土工格栅套筒具有足够的强度和刚度,不因桩体变形而产生塑性变形或出现拉断; ②土工格栅套筒网孔直径小于碎石粒径,且碎石颗粒不会从套筒内鼓出;③在正常工作情况下,桩体和桩周土体视为线弹性体;④仅考虑附加应力对桩体和桩周土体的压缩变形影响,不考虑自重影响;⑤不考虑复合地基的群桩效应;⑥所取微段单元很小,其体积变化量值可忽略。

取桩体及其影响范围内桩周土体组成的单元体为研究对象进行分析,如图2所示，a为桩体半径,b为桩土单元体半径,由桩体间距和布桩方式得

de=cgsd=2b

(4)

式中:de为单元体直径;sd为桩间中心距;cg为布桩方式影响系数(梅花形或正三角形布桩,cg=1.05;正方形布桩,cg=1.13)。在上述条件下,分别探讨加筋碎石桩复合地基加筋段和非加筋段的压缩变形分析方法。

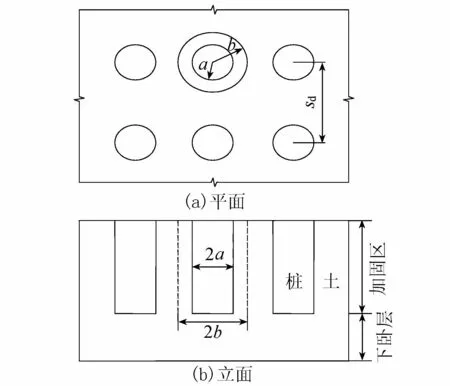
图2 复合地基桩土单元体

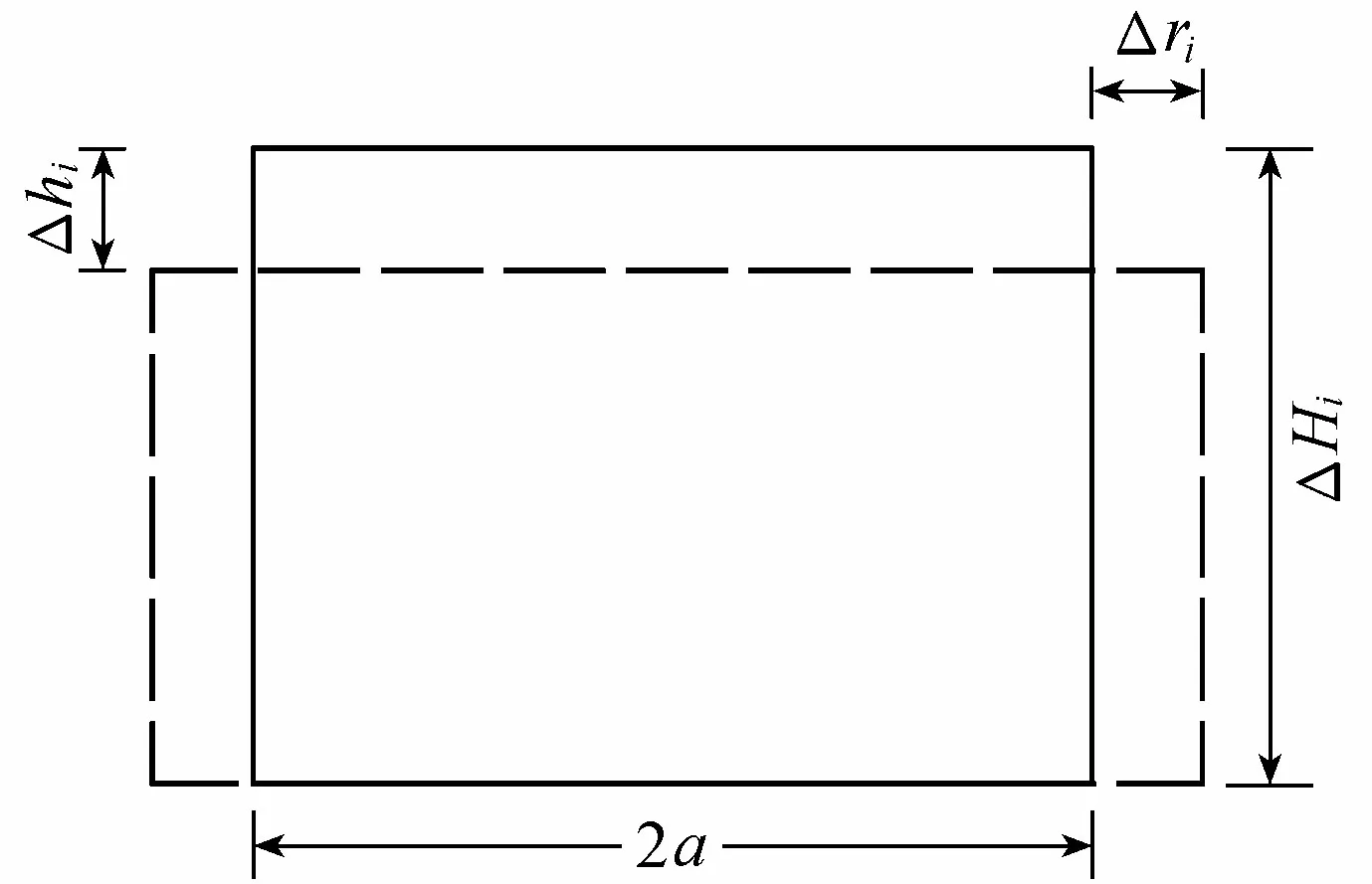
图3 加筋段第i个桩体微段单元变形关系

2.2 加筋段压缩变形分析

针对碎石桩桩体特性和变形特点,本文采用分层迭代法进行压缩变形分析,现将加筋段等分为M个微段单元,加筋段长度为l0,则第i个微段单元厚度ΔHi为

(5)

取加筋段第i个桩体微段单元进行分析,如图3所示。根据基本假定可知,桩体变形均匀且变形前后体积保持不变,同时忽略高阶微量可得

aΔhi=2ΔHiΔri

(6)

式中:Δhi、Δri分别为第i个桩体微段单元的竖向和径向变形量。

(7)

(8)

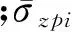
(9)

由式(7)和式(8)可得第i个桩体微段单元产生的竖向和径向变形,即

(10)

(11)

将式(9)代入式(10)和式(11)整理得桩体微段单元底部所受附加应力

σzpi=AiΔhi+BiΔri-σzp(i-1)

(12)

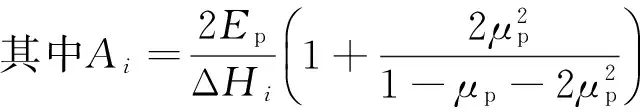
图4 加筋段第i个桩体微段单元受力分析

取第i个桩体微段单元进行受力分析,如图4所示,由桩体竖向静力平衡可得

π (a+Δr(i-1))2σzp(i-1)+2π (a+Δri)·

(ΔHi-Δhi)τi=π(a+Δri)2σzpi

(13)

式中τi为第i个桩体微段单元桩侧平均摩阻力。

联立式(12)和式(13)可得一个关于Δhi的一元二次方程,即

F1iΔhi2+F2iΔhi+F3i=0

(14)

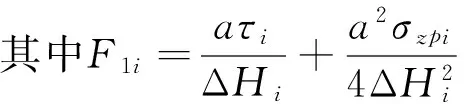
F3i=2a2σzpi-2aτiΔHi

由式(14)计算可得

(15)

而柱侧平均摩阻力

τi=ca+k0pszitanφa

(16)

式中:ca为桩土间的黏聚力;φa为桩土界面的摩擦角;pszi为第i个桩体微段单元中部深度zi处桩周土体竖向附加应力;k0为桩周土的静止土压力系数。

由于桩周土体具有一定的抗剪强度,不可能传递过大的剪应力,因此桩侧摩阻力将与土体的抗剪强度相关联且为一有限值,可认为桩侧摩阻力不超过土体的抗剪强度τ,即整个加筋段桩侧摩阻力:

τz=ca+k0psztanφa≤τ

(17)

2.3 非加筋段压缩变形分析

类似于前述方法,将非加筋段等分为N个桩土微段单元,则第j个桩土微段单元厚度ΔHj为

(18)

由前述分析可知,计算非加筋段压缩变形与加筋段压缩变形一样,需考虑竖向变形和径向变形的影响,只是非加筋段忽略桩土相对滑移并按桩土单元进行分析。因此,非加筋段的压缩变形可借鉴加筋段压缩变形的方法进行分析。取第j个桩土单元体进行受力分析,如图5所示。

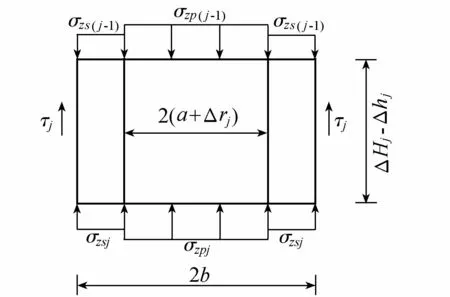
图5 非加筋段第j个桩土单元受力分析

考虑到桩土微段单元的对称性以及桩土单元边界处的应力协调性,桩土微段单元边界处的竖向剪应力τj=0,则由桩土微段单元竖向静力平衡得

π(a+Δr(j-1))2σzp(j-1)+π[b2-(a+Δr(j-1))2]·

σzs(j-1)=π(a+Δrj)2σzpj+π[b2-(a+Δrj)2]σzsj

(19)

式中:Δr(j-1)、Δrj分别为第j-1、j个桩土微段单元径向变形量;σzp(j-1)、σzpj分别为第j-1、j个桩土微段单元桩底竖向应力;σzs(j-1)、σzsj分别为第j-1、j个桩土微段单元土底竖向应力;n(j-1)、nj分别为第j-1、j个桩土单元底部桩土应力比。

按前述加筋段压缩变形计算思路,同理可得第j个桩土微段单元的竖向变形量Δhj的一元三次方程:

(20)

其中λj=[nj(a+Δr(j-1))2+b2]σzp(j-1)+

nj[b2-(a+Δr(j-1))2]σzs(j-1)

式中F1j、F2j表达式见公式(14)中F1i、F2i的表达式，仅需将下标i变化为j。

由式(20)可得解析解,即

(21)

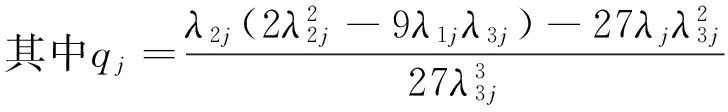
2.4 加固区压缩变形量的计算

(22)

2.5 相关参数的确定方法

上述已建立加筋碎石桩加固区的沉降分析方法,由式(15)和式(21)可知,加固区压缩变形量S1和复合地基几何参数a、b、ΔHi、ΔHj,以及应力应变参数Δri、σzpi、σzsi、Δrj、σzpj、σzsj、nj相关，见式(23)：

S1=F(a,b,ΔHi,ΔHj,Δri,Δrj,

σzpi,σzsi,σzpj,σzsj,nj)

(23)

各应力应变参数确定方法如下：

步骤1确定Δri、Δrj。对于加筋段,Δri为第i+1个桩体微段单元顶部(亦即第i个桩体微段单元底部)径向变形。由于桩体压缩变形分析是从上往下递推,所以第i单元由第i-1单元计算得到,以此类推只要求出径向初始变形Δr0即可求得Δri。由于加筋段第1个桩体微段单元紧接基础或垫层底部,基础或垫层对桩体约束比较大,为简化计算可认为Δr0=0。非加筋段Δrj采用相同方法,其第1个桩体微段单元为加筋段与非加筋段分界面的径向变形,由于受筋材围箍作用和变形协调的影响,其第1个桩土单元顶面的径向变形Δr0等于加筋段第M个桩土单位底部的径向变形。

步骤2确定σzp和σzs。对于加筋段,σzpi为第i+1个桩土单元顶面的竖向附加应力，σzsj为该位置处桩侧土的竖向附加应力。与Δri相同,只需确定初始条件即第1个桩土单元的σzp0和σzs0便可求出,可按下式计算:

(24)

σzp0=pp=nps

(25)

式中:pp、ps分别为复合地基顶部桩、土所受竖向附加应力;p为复合地基顶部所受竖向压力;m为面积置换率;n为桩土应力比,应取实测值为佳,无实测值时可按下式计算[12]:

(26)

式中:Es为土体压缩模量;kp为桩体侧压力系数;ks为桩周土体侧压力系数。

对于非加筋段,由应力连续性可知,非加筋段顶部桩土竖向附加应力等于加筋段底部桩土附加应力,即

(27)

(28)

步骤3确定nj。考虑到碎石桩划分单元体较多且厚度较小,则桩土应力比沿单元体变化很小,为简化计算可假设单元体桩土应力比保持不变,即

(29)

3 工程实例

3.1 实例1

当加筋碎石桩加筋段长度为零时,上述加筋碎石桩复合地基沉降计算方法即可转化为普通碎石桩复合地基沉降计算方法。为验证上述计算方法的通用性和合理性,首先引入一个普通碎石桩复合地基工程实例进行分析。

以文献[14]中某水利工程为例,某水闸拟建于粉土和粉砂地基上,表层2.0～4.5 m为粉土,地基承载力为100 kPa;该层以下是青灰色粉砂,地基承载力为80 kPa。地下水位于地面以下2 m。闸室地基选用了振冲碎石桩加固。文献[14]采用有限元法对碎石桩加固地基进行了分析,模拟桩径1 m,桩长11 m,地基总计算深度12 m,其他具体参数见文献[14]。当上部荷载为150 kPa时,按有限元法计算复合地基沉降为4.76 cm。现利用上述资料采用本文方法对该工程进行沉降计算：复合地基加筋段长度设为零,非加筋段等分为50个单元体,计算得S12=3.97 cm;下卧层采用分层总和法计算得S2=0.87 cm;该工程总沉降量为S=4.84 cm,与有限元法计算结果接近,表明本文方法具有合理性,可退化为普通碎石桩复合地基沉降计算方法。

图6 实例2土层结构及计算参数

3.2 实例2

该工程为四川某高速公路互通式立交桥A匝道,采用土工格栅套筒-碎石桩-砂垫层方法对路基进行加固处理[15]。复合地基参数如下:垫层厚度10 cm,垫层压缩模量20 MPa;加筋碎石桩桩体直径0.6 m,桩长6 m,采用梅花桩布桩,桩间中心距sd=2 m,碎石桩体内摩擦角φp=38°,泊松比μp=0.35,土工格栅套筒加筋深度l0=2 m,加筋段桩体压缩模量Ep=100 MPa,非加筋段Ep=20 MPa,其他土层结构和参数如图6所示。对处理后的路基表面施加平均荷载p=120 kPa,测得桩土应力比n=3.12,路基沉降量S=11.0 cm。

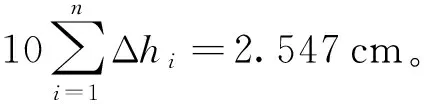
为便于比较分析,现采用其他方法对上述加筋碎石桩工程实例进行计算,结果如表1所示。由表1可知,本文方法与其他方法计算结果都与实测值较为接近。本文方法计算结果比实测值偏大而其他方法偏小。考虑到理论推导一般为地基最终沉降量,而实测值为某一时刻的沉降量,其值一般小于最终沉降,因此本文方法更符合实际情况,避免了现有其他方法分析结果偏于危险的缺陷。因此,采用本文方法计算加筋碎石桩复合地基沉降,不仅计算量较小,而且更具合理性与可行性。但不可否认的是,本文方法仍存在一定的计算误差,其原因主要是研究对象限于采用双向高强土工格栅在碎石桩顶部以下2～3倍桩径深度范围内围箍桩体所形成的加筋碎石桩复合地基,且推导公式时利用了连续均匀介质的假定和弹性力学的基本原理,认为单元体的桩土应力比不变,而实际工程中加筋碎石桩复合地基沉降受许多因素的综合影响,如碎石桩本身具有较大离散性,且当上部荷载较大时,格栅套筒加筋段会出现较大非线性变形,桩土应力比会随着荷载的增大而增大等。

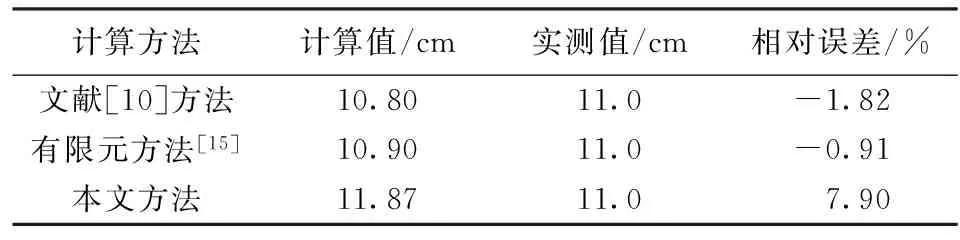
表1 不同方法沉降计算结果

4 结 语

本文结合格栅套筒加筋碎石桩复合地基承载变形机理分析,探讨了此类复合地基的沉降计算方法。理论分析表明,格栅套筒有效限制了碎石桩上半段的径向变形,使得碎石桩桩身上半段呈柔性或半刚性,碎石桩的荷载传递能力更强,变形更小。因此,考虑加筋段桩土存在相对滑移和非加筋段桩土竖向和径向变形协调特征,将加筋碎石桩复合地基分为加筋段、非加筋段和下卧层三部分分别建立沉降计算模型,符合加筋碎石桩复合地基的承载和变形特征,最终推导得出格栅套筒加筋碎石桩复合地基沉降计算公式。工程实例分析表明,本文提出的格栅套筒加筋碎石桩复合地基沉降计算方法具有较高的精度,且克服了现有分析方法计算结果偏于危险的缺陷,更具合理性与可行性。

[1] 王保田, 张福海, 王炳奇.碎石桩复合地基及其在水利工程中的应用[J].水利水电科技进展,2001,21(4):56-58.(WANG Baotian, ZHANG Fuhai, WANG Bingqi. Development of stone column compound foundation and its application in hydraulic projects[J].Advances in Science and Technology of Water Resources, 2001,21(4):56-58. (in Chinese))

[2] 张福海, 王保田, 王炳奇, 等. 大粒径碎石桩在饱和超软土地基中的应用[J].河海大学学报(自然科学版), 2006,34(4):430-434. (ZHANG Fuhai, WANG Baotian, WANG Bingqi, et al. Application of large grain-size gravel piles to strengthening saturated super-soft ground[J].Journal of Hohai University(Natural Sciences), 2006,34(4): 430-434.(in Chinese))

[3] 龚晓南.复合地基理论及工程应用[M].北京: 中国建筑工业出版社, 2007.

[4] 周志刚, 张起森.土工格栅碎石桩的承载力分析[J].岩土工程学报, 1997,19(1):18-21.(ZHOU Zhigang, Zhang Qisen. Analysis on the bearing capacity of geogrid reinforced stone-column[J].Chinese Journal of Geotechnical Engineering, 1997,19(1):18-21.(in Chinese))

[5] 陈昌富, 李其泽.基于圆孔扩张理论顶部加箍碎石桩承载力计算[J].湖南大学学报(自然科学版),2011,38(10):7-12. (CHEN Changfu, LI Qize. Calculation of bearing capacity of geosynthetic-encased gravel pile based on cavity expansion theory[J].Journal of Hunan university(Natural Science), 2011,38(10):7-12.(in Chinese))

[6] 陈昌富, 吴梦婷.基于滑块平衡法顶部加箍碎石桩承载力计算方法[J].岩土工程学报, 2013,35(7):1253-1260. (CHEN Changfu, WU Mengting. Computational method for bearing capacity of upper geosynthetic-encased stone columns based on block limit equilibrium method[J].Chinese Journal of Geotechnical Engineering, 2013,35(7):1253-1260.(in Chinese))

[7] 王纯子, 陈昌富, 赵阳.顶部加箍碎石桩极限承载力上限分析[J].岩土力学, 2015,36(6):1801-1805. (WANG Chunzi, CHEN Changfu, ZHAO Yang. Upper-bound limit analysis of ultimate bearing capacity of upper geosynthetic-encased stone column[J].Rock and Soil Mechanics, 2015,36(6):1801-1805.(in Chinese))

[8] 赵明华, 陈庆, 张玲, 等.加筋碎石桩承载力计算[J].公路交通科技, 2011,28(8):7-12. (ZHAO Minghua, CHEN Qing, ZHANG Ling, et al. Calculation of bearing capacity of geosynthetic-encased stone columns[J]. Journal of Highway and Transportation Research and Development, 2011,28(8):7-12. (in Chinese))

[9] 赵明华, 张赞威, 刘猛, 等.筋箍碎石桩复合地基极限承载力计算[J].水文地质工程地质, 2014,41(1):67-73. (ZHAO Minghua, ZHANG Zanwei, LIU Meng, et al. Calculation of ultimate bearing capacity of composite foundation with geosynthetic encased stone columns[J]. Hydrogeology & Engineering Geology, 2014,41(1):67-73 (in Chinese))

[10] 曹文贵,杨泽华.柔性基础下碎石桩加筋复合地基沉降分析方法[J].岩土工程学报,2012,34(11): 1997-2004.(CAO Wengui, YANG Zehua. Method for analyzing settlement of reinforced-pile composite ground under flexible foundation[J].Chinese Journal of Geotechnical Engineering, 2012,34(11): 1997-2004.(in Chinese))

[11] 吴梦婷,陈昌富.顶部加箍碎石桩复合地基沉降计算方法[J].中国科技论文,2013,8(11):1095-1099. (WU Mengting, CHEN Changfu. Settlement computation of composite foundation of upper geosynthetic-encased stone column[J]. China Science Paper, 2013,8(11):1095-1099.(in Chinese))

[12] 高明军.管式格栅加筋碎石桩的承载特性试验研究[D].南京:河海大学,2008.

[13] BAUMANN V, BAUER G E A. The performance of foundation on various soils stabilized by the vibro-compaction method[J].Canadian Geotechnical Journal,1974,3(2):509-530.

[14] 俞伟, 苏枋, 唐新军.碎石桩加固软土地基处理的有限元分析[J].水利与建筑工程学报, 2013,11(5):114-117. (YU Wei, SU Fang, TANG Xinjun. Finite element analysis on soft soil foundation reinforcement with gravel pile[J]. Journal of Water Resources and Architectural Engineering, 2013,11(5):114-117.(in Chinese))

[15] 黄兵.GSPS软基加固系统机理及其在成都绕城高速公路的应用研究[D].成都:西南交通大学,2002.

Calculation method for settlement of composite foundation reinforced with geogrid-encased stone columns

HE Chengbin1,2, ZHAO Minghua1, MA Binhui2, CHEN Qiunan2, LEI Yong2

(1.CollegeofCivilEngineering,HunanUniversity,Changsha410082,China; 2.SchoolofCivilEngineering,HunanUniversityofScienceandTechnology,Xiangtan411201,China)

An analysis of the bearing and deformation mechanism of a composite foundation reinforced with geogrid-encased stone columns is presented in order to obtain its bearing characteristic and settlement calculation method. The composite foundation is divided into three parts: the reinforced section, the unreinforced section, and the underlying stratum. Based on the Hooke’s law of space problem and layer summation method, the settlement of the reinforced section is calculated with the layered iteration method in view of the relative slip displacement between the pile and soil of the reinforced section without a plastic zone. The compatibility of vertical and radial deformation of the unreinforced section is analyzed based on the pile-soil element model. The settlement of the underlying stratum is calculated by the layer summation method. Therefore, the calculation formula can be derived for a composite foundation reinforced with geogrid-encased stone columns. The results of engineering examples show that the settlement result obtained from this method is close to the measured one. Furthermore, the method is more feasible and can be applied in engineering practice, whereas the results calculated with other available methods are more dangerous.

geogrid-encase;reinforced stone column; settlement calculation; vertical deformation; radial deformation; relative slip between pile and soil

国家自然科学基金(51308208,41372303)

贺成斌(1974—),男,讲师,博士,主要从事地基处理研究。E-mail:chengbinhe@163.com

10.3880/j.issn.1006-7647.2017.02.016

U416.1

：A

：1006-7647(2017)02-0088-07

2015-11-09 编辑：骆超)