基于起裂韧度准则的混凝土裂缝黏聚区特性

卿龙邦,聂雅彤

(河北工业大学土木与交通学院,天津 300401)

基于起裂韧度准则的混凝土裂缝黏聚区特性

卿龙邦,聂雅彤

(河北工业大学土木与交通学院,天津 300401)

基于起裂韧度扩展准则和黏聚裂缝模型研究混凝土断裂全过程中的裂缝尖端黏聚区特性；利用不同尺寸的带裂缝三点弯曲梁试件,计算得到了裂缝尖端黏聚区的长度、黏聚力、裂缝张开位移等,并采用现有试验成果和有限元方法计算成果对本文结果进行了验证。分析结果表明：最大黏聚区长度以及峰值时刻对应的临界黏聚区长度随试件尺寸增大而逐渐增大,最大黏聚区长度受拉伸软化曲线影响;裂缝断裂全过程曲线受软化曲线影响较小;当外荷载达到峰值后裂缝张开位移近似为线性分布,黏聚力分布受拉伸软化曲线影响较大。

混凝土;黏聚区;起裂韧度;裂缝张开位移;黏聚力

众所周知,混凝土裂缝尖端存在断裂过程区。断裂过程区的存在,使得实验室小尺寸混凝土断裂试件断裂参数的测试结果出现尺寸效应[1],导致线弹性断裂力学无法直接适用。因此,研究断裂过程区特性,是进行混凝土非线性断裂分析的重要前提。为考虑混凝土裂缝断裂过程区的影响,受Dugdale等[2-3]的启发,Hillerborg等[4]将黏聚裂缝模型概念应用到混凝土中,提出了适用于混凝土的黏聚裂缝模型,也称虚拟裂缝模型,该模型将裂缝尖端应力达到抗拉强度作为裂缝开裂准则,将黏聚区视为能传递应力的虚拟裂缝,其裂缝面上的黏聚力与裂缝张开位移满足拉伸软化关系,拉伸软化关系亦被Bazant等[5]应用于裂缝带模型。基于虚拟裂缝模型,学者们开展了大量断裂全过程及黏聚区研究[6-11]。

Jenq等[12-13]指出,当外荷载达到起裂荷载时,混凝土裂缝开始非线性扩展,裂缝尖端应力状态随裂缝起裂发生改变。徐世烺等[14]首先提出将起裂韧度作为裂缝开裂的判别准则,并将裂缝起裂时对应的裂缝尖端应力强度因子定义为起裂韧度。混凝土裂缝起裂,可视为裂缝尖端材料发生宏观损伤破坏的起始,即裂缝尖端应力强度因子若达到了起裂韧度,标志着材料开始发生损伤破坏。因此,起裂韧度可看作是材料抵抗裂缝开裂的能力。吴智敏等[15-16]提出将起裂韧度作为裂缝扩展准则,不同于虚拟裂缝模型的强度准则,基于起裂韧度扩展准则时,当外荷载与黏聚力分别引起的应力强度因子相叠加达到起裂韧度时,裂缝开始扩展。

起裂韧度可通过起裂荷载和初始缝长利用线弹性断裂力学公式计算[14]。起裂荷载可采用光弹、散斑、电阻应变片等试验方法或理论方法得到。其中,徐世烺等[17]提出了确定起裂韧度的双K方法,基于此方法,Kumar等[18]采用简化的权函数方法获得了起裂韧度。Zhang等[19]将不同获取起裂韧度的方法进行了对比研究。Reinhardt等[20-21]利用P-CMOD(荷载-裂缝口张开位移)曲线由线性到非线性的转变点来确定起裂荷载,进而求得起裂韧度。Qing等[22]提出了一种利用峰值荷载确定起裂韧度的方法。

基于起裂韧度扩展准则可模拟断裂全过程,且取得了较好的结果。基于起裂韧度准则,Dong等[16]利用有限元方法研究了混凝土带裂缝三点弯曲梁的断裂全过程模拟方法。李庆斌等[23-24]将起裂断裂韧度作为裂缝扩展准则,利用数值方法分别研究了楔入劈拉试件和三点弯曲梁混凝土试件的裂缝扩展分析方法。Zhang等[21]提出了采用断裂全过程的数值方法,并分别利用强度准则和韧度准则研究了软化曲线的获取方法。吴智敏等[25]提出了Ⅰ-Ⅱ复合型裂缝的扩展分析方法。对于带裂缝的结构而言,与基于强度开裂准则的虚拟裂缝模型分析方法相比,考虑起裂韧度的分析方法通常能更准确反映出裂缝的起裂状态。

混凝土黏聚区特性对断裂全过程具有决定性的影响,但以往研究并不全面。关于黏聚区上的黏聚力分布形式,常假设为线性分布或双线性分布[13-14,17-20]。Dong等[16,26]研究表明黏聚区长度随裂缝扩展发生变化,且其变化对KR阻力曲线具有一定的影响。然而,考虑起裂韧度的黏聚区研究较少,导致对黏聚区黏聚力及裂缝张开位移分布尚未形成统一的认识。由于黏聚区特性对断裂全过程的快速准确预测以及对结构安全评定等方面具有重要的意义,因此,基于起裂韧度准则的黏聚区特性,包括黏聚区的长度、黏聚力、裂缝张开位移等特性有待于进一步深入研究。本文利用三点弯曲梁对混凝土断裂全过程进行计算,并研究混凝土黏聚区长度、裂缝张开位移分布、黏聚力分布等黏聚区特性。

1 计算模型与方法

1.1 计算模型

三点弯曲梁模型如图1所示,图中B、D、S分别为梁的厚度、高度和有效跨度,a0为初始裂缝长度,P为外荷载,a为引入黏聚裂缝后的有效裂缝长度,σ为黏聚区上的黏聚力。

图1 考虑黏聚力的三点弯曲梁模型

根据线性叠加原理,图1所示模型中的荷载可分解为外荷载和黏聚力这两部分作用的叠加。应力强度因子及位移亦可进行叠加。

1.1.1 外荷载表达式

外荷载在有效裂缝尖端处产生的应力强度因子[27]为

(1)

(2)

对于任意a/D,式(2)的精度为0.5%。

黏聚力在有效裂缝尖端处产生的应力强度因子Kσ可采用无限长条板的应力强度因子近似计算[13],Kσ表达式[27]为

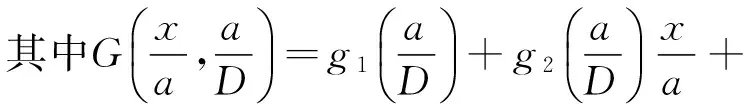
式中x为黏聚力作用位置与裂缝尖端处的距离。

由线性叠加原理,裂缝尖端应力强度因子KⅠ等于外荷载在有效裂缝尖端处产生的应力强度因子KP与黏聚区上的黏聚力在有效裂缝尖端处产生的应力强度因子Kσ之和:

KⅠ=KP+Kσ

(4)

根据起裂韧度扩展准则[16],可推导得外荷载表达式:

(5)

式中Kini为起裂韧度。

1.1.2 裂缝张开位移表达式

同理,依据叠加原理,裂缝张开位移表达式为

δ=δ1+δ2

(6)

式中:δ1为外荷载产生的裂缝张开位移；δ2为黏聚力产生的裂缝张开位移,可利用由卡氏定理推导的Paris位移公式表示[28]。

由外荷载产生的裂缝张开位移为

(7)

式中:E为混凝土弹性模量;ξ为积分变量。

由黏聚力产生的裂缝张开位移为

(8)

式中b为积分变量。

1.1.3 拉伸软化曲线

黏聚力与裂缝张开位移之间的关系采用拉伸软化曲线[4,22]表示:

σ=f(δ，ft,w0,…)

(9)

式中:ft为单轴拉伸强度;w0为最大裂缝张开度。

结合式(5)(6)(9)即可得到求解断裂全过程的控制方程组。

1.2 裂缝扩展的模拟方法与步骤

混凝土裂缝断裂全过程的模拟可分为起裂前和起裂后两个阶段[24]。在裂缝起裂前,采用荷载控制方式,断裂过程可直接采用线弹性断裂力学公式计算,裂缝尖端应力强度因子达到起裂韧度时,裂缝起裂。裂缝起裂后,以裂缝有效长度作为加载方式,计算每一步裂缝有效长度下对应的裂缝张开位移、外荷载等参数,当裂缝有效缝长即将达到试件的边界时,计算终止。其中数值计算可采用迭代方法。

由于起裂前不形成黏聚区,裂缝尖端张开位移和裂缝扩展长度值均为零,因此只需利用式(5)(7)计算外荷载和裂缝张开位移即可。

起裂后,裂缝开始扩展。根据上节的推导可知,外荷载表达式(式(5))、裂缝张开位移表达式(式(6))、拉伸软化曲线(式(9))3式中含有黏聚力、裂缝张开位移、有效裂缝长度等未知数，在给定有效裂缝长度的情况下,其他参数可通过联立上述3式求解。因此,将有效裂缝长度由零逐渐增大,即可求得扩展阶段的变化曲线，具体步骤如下:

a. 设定有效裂缝长度扩展量Δa,初始值为零。

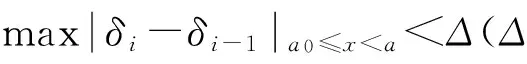
c. 根据式(6)计算裂缝张开位移。

d. 将有效裂缝长度与试件高度对比,若试件高度大于有效裂缝长度,则增加扩展量,并回到第b步继续计算。若试件高度等于或小于有效裂缝长度,则计算终止。

根据上述步骤,若已知试验的起裂荷载以及拉伸软化曲线,即可确定裂缝扩展全曲线及扩展中黏聚区上的裂缝张开位移及黏聚力分布。

2 结果与讨论

2.1 计算结果与有限元方法结果比较

为研究不同尺寸的混凝土三点弯曲梁黏聚区特性,利用文献[16]文中的L系列试件进行计算。

式(9)中的σ与δ满足拉伸软化本构关系,本文取为双折线形式:

式中σs、ws为材料参数,Petersson[6]给出的参数取值为σs=ft/3,ws=0.8GF/ft,w0=3.6GF/ft,其中GF为混凝土断裂能。

L系列试件的初始缝长比均相同,但试件高度的范围为100～300 mm。最大骨料粒径为10 mm,单轴拉伸强度ft=2.3 MPa,弹性模量E=28 GPa,泊松比ν=0.2。试件主要参数见表1。

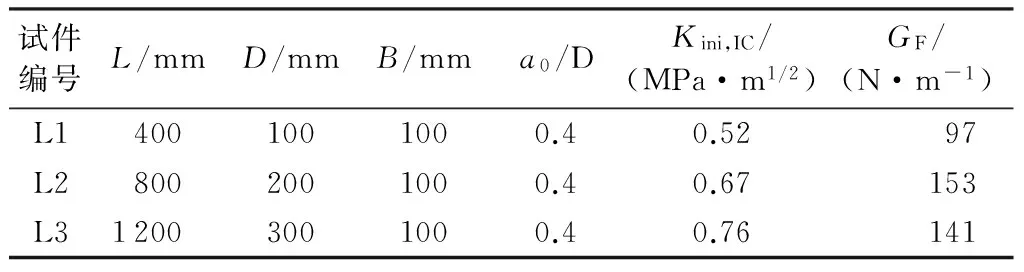
表1 试件尺寸与材料参数

图2是采用本文提出的方法计算的L系列试件的P-CMOD曲线与文献[16]中的有限元方法计算结果的对比。表2是L系列试件峰值荷载时刻的计算结果。由图2和表2可以看出,本文方法计算结果与有限元方法计算结果吻合较好。

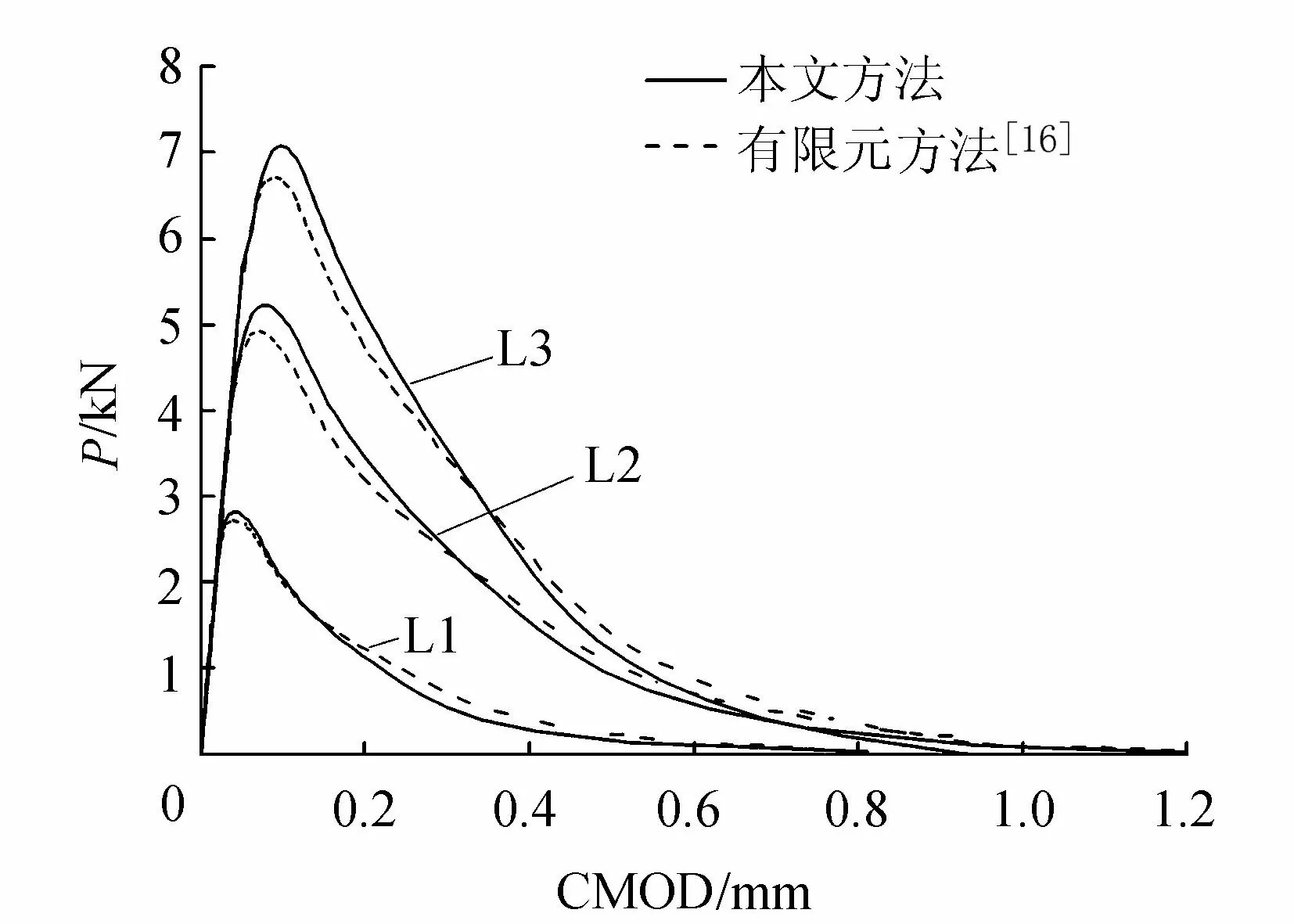
图2 L系列试件的P-CMOD曲线

表2 L系列试件峰值荷载时刻的计算结果

注:CTODc为峰值荷载时刻裂缝尖端张开位移。

2.2 软化曲线对计算结果的影响

为分析软化曲线对黏聚区特性的影响,采用另一组软化曲线进行计算。Reinhardt等[29]提出的软化曲线表达式为

(11)

式中:c1、c2为材料参数,c1=3,c2=6.93;w0=5.14GF/ft。

图3为L系列试件采用不同软化曲线计算的P-CMOD全曲线对比,可以看出,不同软化曲线对计算结果的影响非常小。

图3 软化曲线对L系列试件P-CMOD全曲线的影响

2.3 黏聚区特性分析

最大黏聚区长度如表3所示,可以看出,与临界断裂过程区规律相似,最大黏聚区长度随试件尺寸增大而逐渐增大，该结论与Dong等[16]利用有限元方法研究的结论相同。此外,最大黏聚区长度受拉伸软化曲线影响,采用式(11)计算的结果大于采用式(10)计算的结果。

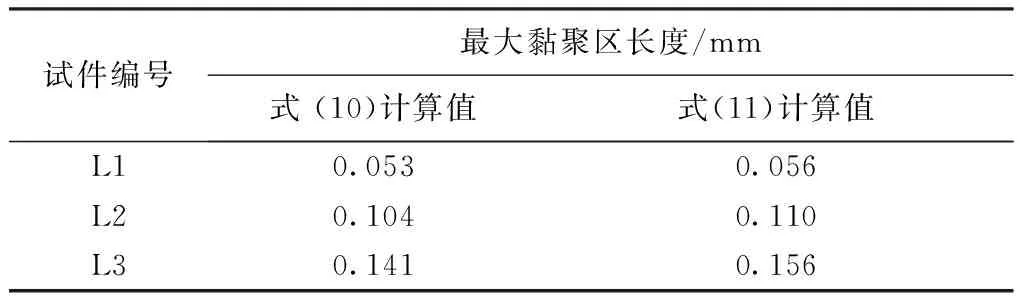
表3 最大黏聚区长度

利用L2试件分析断裂过程中裂缝张开位移与黏聚力的分布规律。图4为L2试件P-CMOD曲线,0～6对应于不同时刻,0代表起裂点,1代表起裂后未达到峰值时刻的某一点,2代表峰值时刻点,3、4、5、6代表P-CMOD曲线下降段上的时刻点,其中5和6分别代表采用两种软化曲线计算的初始裂缝尖端应力为零时所对应的时刻点,即对应于黏聚区最长的时刻点。图5为L2试件的P-a/D曲线,其中的0～6分别对应于图4中的6个时刻。

图6、图7分别为采用式(10)和式(11)的软化曲线时,L2试件不同时刻点(0～6)对应的裂缝张开位移与黏聚力分布。由图6可以看出,起初裂缝张开位移为非线性分布,当外荷载达到峰值荷载或黏聚区长度较大后,裂缝张开位移基本为线性分布。Foote等[30]的黏聚区特性研究结果也表明,裂缝尖端位移为线性分布。

由图7(a)可以看出,黏聚力初始情况为线性分布,然后为双线性分布,初始裂缝尖端应力为零后,为三线性分布。由图7(b)可以看出,黏聚力一直为光滑的非线性曲线分布,可推断黏聚力分布形式与拉伸软化曲线相关。

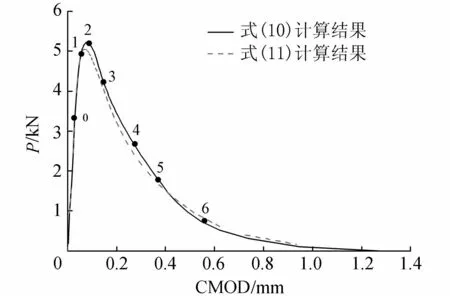
图4 L2试件P-CMOD全曲线

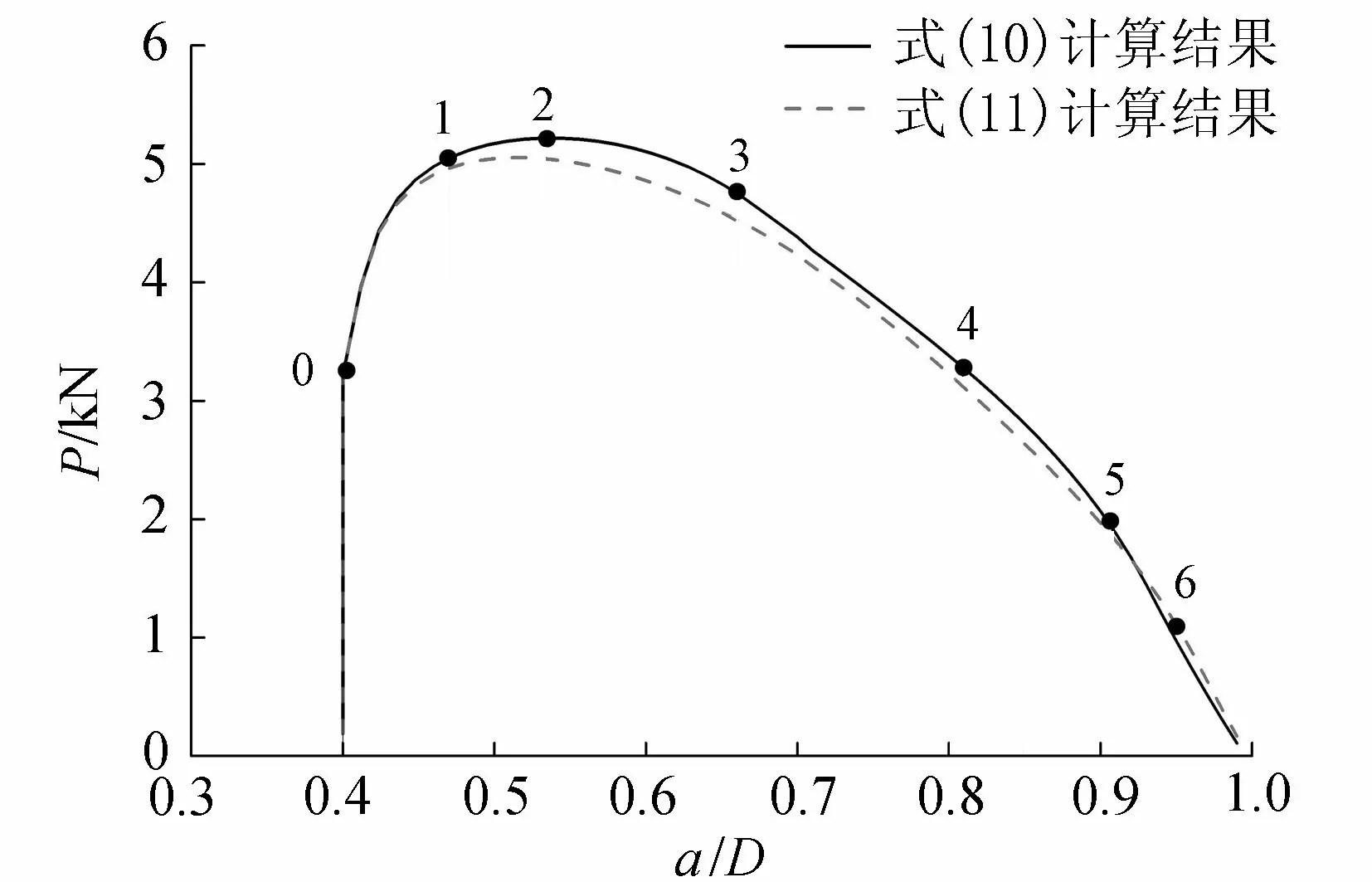
图5 L2试件P- a/D全曲线

图6 L2试件断裂过程中的裂缝张开位移

图7 L2 试件断裂过程中的黏聚力

3 结 论

a. 最大黏聚区长度及峰值时刻对应的临界黏聚区长度均随试件高度增大而逐渐增大。其长度受拉伸软化曲线影响。

b. 拉伸软化曲线对断裂全过程P-CMOD曲线影响较小。

c. 荷载达到峰值前黏聚区裂缝张开位移和黏聚力均为非线性分布,荷载达到峰值后黏聚区裂缝张开位移近似为线性分布,黏聚力为非线性分布,其形式与拉伸软化曲线有关。

[1] BAZANT Z P,PLANAS J.Fracture and size effect in concrete and other quasi brittle materials[M].Boca Raton:CRC Press,1998.

[2] DUGDALE D S.Yielding of steel sheets containing slits[J].Journal of the Mechanics & Physics of Solids,1960,8(2):100-104.

[3] BARENBLATT G I.The mechanical theory of equilibrium cracks in brittle fracture[J].Advances in Applied Mechanics,1962,7:55-129.

[4] HILLERBORG A,MODEER M,PETERSSON P E.Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J].Cement & Concrete Research,1976,6(6):773-781.

[5] BAZANT Z P,CEDOLIN L.Blunt crack band propagation in finite element analysis[J].Journal of the Engineering Mechanics Division,1979,105:297-315.

[6] PETERSSON P E.Crack growth and development of fracture zones in plain concrete and similar materials[M].Lund: Lund Institute of Technology,1981.

[7] STANG H,OLESEN J F,POULSEN P N,et al.On the application of cohesive crack modeling in cementitious materials[J].Materials & Structures,2007,40(4):365-374.

[8] 卿龙邦,李庆斌,管俊峰,等.基于虚拟裂缝模型的混凝土断裂过程区研究[J].工程力学,2012,29(9):112-116.(QING Longbang,LI Qingbin,GUAN Junfeng,et al.Study of concrete fracture process zone based on fictitious crack model[J].Engineering Mechanics,2012,29(9):112-116.(in Chinese))

[9] KARIHALOO B L,XIAO Q Z.Asymptotic fields at the tip of a cohesive crack[J].International Journal of Fracture,2008,150(1/2):55-74.

[10] 曹亮,王向东.三点弯曲试件混凝土KIC尺寸效应公式的修正[J].河海大学学报(自然科学版),2007,35(1):63-66.(CAO Liang,WANG Xiangdong.Modification of size effect formula of fracture toughness of concrete for three-point bending specimens[J].Journal of Hohai University (Natural Sciences),2007,35(1):63-66.(in Chinese))

[11] 吴熙,范兴朗,吴智敏.自密实轻骨料混凝土断裂全过程分析[J].水利水电科技进展,2014(6):36-39.(WU Xi,FAN Xinglang,WU Zhimin.Analysis of crack propagation in self-compacting lightweight concrete[J].Advances in Science and Technology of Water Resources,2014,34(6):36-39.(in Chinese))

[12] JENQ Y S,SHAH S P.Two parameter fracture model for concrete[J].Journal of Engineering Mechanics,1985,111:1227-1241.

[13] JENQ Y S,SHAH S P.A fracture toughness criterion for concrete[J].Engineering Fracture Mechanics,1985,21(5):1055-1069.

[14] XU S L,REINHARDT H W.Determination of double-Kcriterion for crack propagation in quasi-brittle fracture:part I.experimental investigation of crack propagation[J].International Journal of Fracture,1999,98(2):111-149.

[15] 吴智敏,董伟,刘康,等.混凝土Ⅰ型裂缝扩展准则及裂缝扩展全过程的数值模拟[J].水利学报,2007,38(12):1453-1459.(WU Zhimin,DONG Wei,LIU Kang,et al.ModeⅠcrack propagation criterion of concrete and numerical simulation on complete process of cracking[J].Journal of Hydraulic Engineering,2007,38(12):1453-1459.(in Chinese))

[16] DONG W,WU Z M,ZHOU X M.Calculating crack extension resistance of concrete based on a new crack propagation criterion[J].Construction & Building Materials,2013,38:879-889.

[17] XU S L,REINHARDT H W.Determination of double-Kcriterion for crack propagation in quasi-brittle fracture:part Ⅱ.Analytical evaluating and practical measuring methods for three-point bending notched beams[J].International Journal Fracture,1999,98(2):151-177.

[18] KUMAR S,BARAI S V.Determining double-Kfracture parameters of concrete for compact tension and wedge splitting tests using weight function[J].Engineering Fracture Mechanics,2009,76(7):935-948.

[19] ZHANG X F,XU S L.A comparative study on five approaches to evaluate double-Kfracture toughness parameters of concrete and size effect analysis[J].Engineering Fracture Mechanics,2011,78(10):2115-2138.

[20] REINHARDT H W,XU S L.Crack extension resistance based on the cohesive force in concrete[J].Engineering Fracture Mechanics,1999,64(5):563-587.

[21] ZHANG J,LEUNG C K Y,XU S L.Evaluation of fracture parameters of concrete from bending test using inverse analysis approach[J].Materials & Structures,2010,43(6):857-874.

[22] QING L B,LI Q B.A theoretical method for determining initiation toughness based on experimental peak load[J].Engineering Fracture Mechanics,2013,99(1):295-305.

[23] 李庆斌,卿龙邦,管俊峰.混凝土裂缝断裂全过程受黏聚力分布的影响分析[J].水利学报,2012,43(增刊1):31-36.(LI Qingbin,QING Longbang,GUAN Junfeng.Analysis of the whole fracture process of concrete considering effects of cohesive distribution[J].Journal of Hydraulic Engineering,2012,43(Sup1):31-36.(in Chinese))

[24] 管俊峰,卿龙邦,赵顺波.混凝土三点弯曲梁裂缝断裂全过程数值模拟研究[J].计算力学学报,2013,30(1):143-148.(GUAN Junfeng,QING Longbang,ZHAO Shunbo.Research on numerical simulation on complete process of cracking for three-point bending notch beams[J].Chinese Journal of Computer Mechanics,2013,30(1):143-148.(in Chinese))

[25] WU Z M,RONG H,ZHENG J J,et al.Numerical method for mixed-mode Ⅰ-Ⅱ crack propagation in concrete[J].Journal of Engineering Mechanics,2013,139(11):1530-1538.

[26] XU F,WU Z M,ZHENG J J,et al.Crack extension resistance curve of concrete considering variation of FPZ length[J].Journal of Materials in Civil Engineering,2014,23(5):703-710.

[27] TADA H,PARIS P C,IRWIN G.The stress analysis of crack handbook[M].New York:ASME Press,2000.

[28] PARIS P C,ERDOGAN F.A critical analysis of crack propagation laws[J].Journal of Basic Engineering,1963,85(4):528-533.

[29] REINHARDT H W,COMELISSEN H A W,HORDJIL D A.Tensile tests and failure analysis of concrete[J].Journal of Structural Engineering,1986,112(11):2462-2477.

[30] FOOTE R M L,MAI Y W,COTTERELL B.Crack growth resistance curves in strain-softening materials[J].Journal of the Mechanics & Physics of Solids,1986,34(6):593-607.

Characteristics of cohesive zone of concrete cracks based on initial fracture toughness criterion

QING Longbang, NIE Yatong

(SchoolofCivilEngineeringandTransportation,HebeiUniversityofTechnology,Tianjin300401,China)

The characteristics of the cohesive zone at crack tips throughout the fracture process were studied based on the initial fracture toughness (IFT) criterion and cohesive crack model. Single-edge notched beams with different sizes, subjected to three-point bending, were used as specimens, and the length of the cohesive zone at crack tips, the cohesive stress of concrete, and the crack opening displacement (COD) were calculated. The calculated results were verified with the results from tests and the finite element method (FEM). Results show that the maximum and critical lengths of the cohesive zone increase with the size of specimens; the maximum length of the cohesive zone is influenced by the tensile softening curve, while the whole fracture process is slightly affected by the tensile softening curve; after the peak load is reached, the COD is approximately linearly distributed; and the distribution of cohesive stresses depends on the tensile softening curve.

concrete; cohesive zone; initial fracture toughness; crack opening displacement; cohesive stress

国家自然科学基金(51309073);河北省自然科学基金(E2014202257);高等学校博士学科点专项科研基金(20131317120012)

卿龙邦(1982—),男,副教授,博士,主要从事混凝土断裂及损伤研究。E-mail:qlongbang@126.com

10.3880/j.issn.1006-7647.2017.02.007

TU528.0

：A

：1006-7647(2017)02-0037-06

2016-02-04 编辑：熊水斌)