直叶H型潮流水轮机三维数值模拟

2017-03-15付士凤梁晓玲陈会向杨春霞

水利水电科技进展 2017年2期

关键词：垂直轴转轮水轮机

付士凤,郑源,梁晓玲,阚阚,陈会向,杨春霞

(1.河海大学水利水电学院,江苏南京 210098; 2.河海大学文天学院,安徽马鞍山 243031)

直叶H型潮流水轮机三维数值模拟

付士凤1,郑源1,梁晓玲2,阚阚1,陈会向1,杨春霞1

(1.河海大学水利水电学院,江苏南京 210098; 2.河海大学文天学院,安徽马鞍山 243031)

为了探究直叶H型潮流水轮机水动力性能的影响因素,在理论分析的基础上,应用大型建模软件UG建立了直叶H型潮流水轮机三维模型,基于滑移网格技术采用Fluent软件对水轮机模型进行三维数值模拟,在保持直叶H型潮流水轮机叶片翼型一定、水轮机密实度相同的条件下,通过改变转轮叶片数以及来流速度,分析了潮流水轮机水动力性能。结果表明,叶片数对直叶H型潮流水轮机水动力性能影响很大,叶片数越多,输出扭矩值越小,当叶片数为3、叶尖速比为1.63时,水轮机最高获能系数为31.21%。

潮流水轮机;直叶;翼型;水动力性能;数值模拟

随着煤炭、石油等化石能源不断消耗,使用成本逐渐提高,能源供需矛盾越来越突出,作为一种可再生清洁能源,潮流能的开发与研究备受关注[1]。我国潮流能资源十分丰富,蕴含总量达1.4亿kW,在潮流能开发及利用方面具有得天独厚的优越条件[2]。在能源问题日显突出的今天,加大潮流能资源的开发力度是解决能源问题进程中必不可少的一环。

近些年来,垂直轴潮流水轮机发展迅速,加拿大Blue Energy公司研制了功率为100 kW垂直轴样机[3]；意大利PDA公司漂浮式垂直轴直叶片变桨水轮机于2002年在墨西哥海峡运行[4];美国GCK Technology公司开发的垂直轴潮流水轮机(GHT)采用旋转一定角度的螺旋形叶片,螺旋形叶片的垂直轴潮流水轮机相对于直叶片的垂直轴潮流水轮机具有运行平稳、容易启动的优点[5];韩国引进美国技术建造了潮流能实验电站,在珍岛郡鸣梁海峡大桥下游安装了两台500 kW垂直轴潮流水轮机,并投入正式运营[6];中国海洋大学研制了一款漂浮式垂直轴潮流水轮机发电装置[7],采用柔性叶片,类似于帆翼,其突出特点是可以充分有效地利用升阻力效应,该垂直轴潮流水轮机发电装置在青岛胶南斋堂岛海域成功进行了测试,取得良好的效果；哈尔滨工程大学设计研制的“万向Ⅰ”号漂浮式潮流水轮机,输出功率可达70 kW[8],并且在浙江省岱山县又建造了“万向Ⅱ”号40 kW座海底式潮流水轮机[9]。在潮流水轮机研究方面,张楠[10]对漂浮式潮流水轮机的叶轮及锚泊系统进行了研究,提出了一种极限海况下安全可靠的锚泊系统;张亮等[11]研究了导流罩与转轮之间流体动力学的干扰规律,认为导流罩可稳定下游流场;罗庆杰等[12]采用UDF控制滑移网格方法,可对摆线式直叶H型潮流水轮机性能进行预报；付士凤等[13]的研究表明,直叶H型潮流水轮机的优点在于叶片结构简单,不需要对流装置,维护成本低。目前有关潮流能水力机械的研究多数都集中于单一因素的分析,对影响直叶H型潮流水轮机水动力性能的综合因素研究较少。基于此,本文结合理论分析与三维数值模拟,研究在不同叶片数和来流速度条件下,直叶H型潮流水轮机水力特性及利用效率,可为垂直轴潮流水轮机研究设计提供参考。

1 物理模型

1.1 几何建模

在保持水轮机密实度一定的条件下,利用大型三维建模软件UG对直叶H型潮流水轮机转轮进行三维造型,如图1所示。

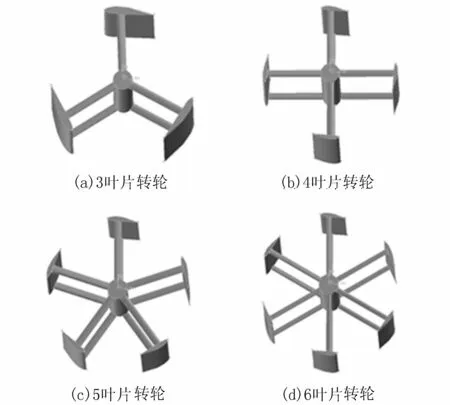
图1 直叶H型潮流水轮机转轮三维造型

对于直叶H型潮流水轮机,密实度定义为

(1)

式中:z为叶片数;c为弦长;d为转轮直径。由文献[14]可知水轮机密实度取值在0.15～0.5之间,取值过小、过大都不利于潮流能的有效利用,本文取为0.35。

1.2 受力分析

直叶H型潮流水轮机直叶片断面受力分析如图2所示(图中L为升力;D为阻力;v为来流速度;u为叶片旋转沿切线速度;w为相对流速;α为攻角;θ为叶片的相位角,用来定义叶片所处的位置)。直叶H型潮流水轮机主要利用了水流对叶片的升力来驱动转轮旋转。

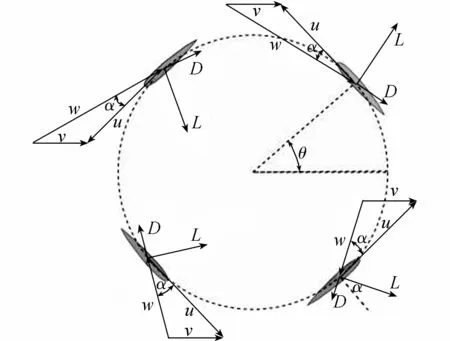
图2 直叶H型潮流水轮机直叶片断面受力分析示意图

1.3 水轮机模型参数

直叶H型潮流水轮机模型参数如下:水轮机外径D1=3.5 m,水轮机轮毂直径D2=0.5 m,叶片高度h=4 m,叶片安装角φ=-7°，叶片数z=3、4、5、6,主翼型为NACA4415,支撑架翼型为NACA0015,主翼型的弦长C1=1.28 m、0.96 m、0.77 m、0.64 m。

2 三维数值模拟计算

2.1CFD计算方法

直叶H型潮流水轮机运行时,外部流动的水为不可压缩流体,转轮叶片表面主要受到重力、水压力和离心力的作用,应用Fluent软件,采用雷诺时均Navier-Stokes方程[15]和Spalart-Allmaras湍流模型[16]对垂直轴水轮机转轮区域流场进行CFD数值模拟,连续性方程和Navier-Stokes方程分别为

(2)

(3)

式中:u为流体速度矢量;F为质量力;p为压强;ρ为流体密度;μ为湍流黏度。计算采用二阶迎风格式,非定常隐式求解,时间步长为0.01 s,利用SIMPLEC算法实现压力和速度的耦合。

2.2 边界条件

进水流道入口处的边界条件设置为速度进口;水轮机所处的圆柱体表面定义为滑移面,在假定压强已经恢复到来流静压的条件下,下游出水流道断面处边界条件设置为平均静压出口;对于不可压缩流体,转轮、支架叶片及流道表面的边界条件设置为无滑移绝热固壁。

2.3 计算域网格划分

实际上,直叶H型潮流水轮机运行在海洋中,所处区域广阔,本文根据水轮机模型的基本参数建立一个长方形区域为直叶H型潮流水轮机周围的流动区域,同时把它作为计算区域,取水轮机转轴中心点为坐标原点,如图3所示。

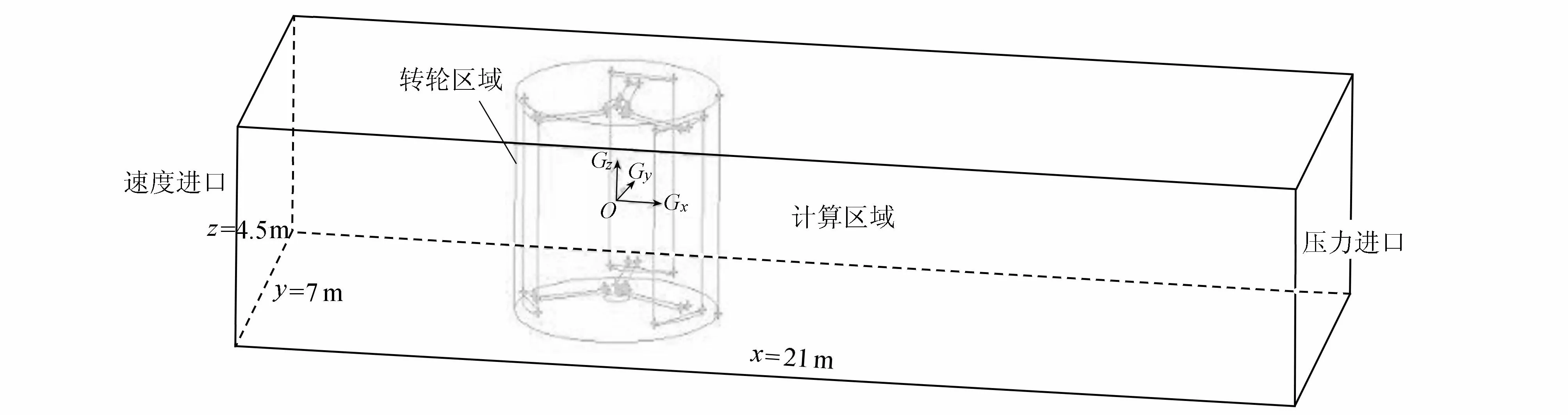
图3 计算区域

为了确保模拟计算的准确性,进一步将计算区域划分成两部分,以一紧密环绕直叶H型潮流水轮机的圆柱体区域为第一部分,对此区域内的网格进行细化加密,并同时定义圆柱体表面为滑移边界,除此之外的长方体流动区域为第二部分。运用ANSYS ICEM软件对两个区域进行网格划分,鉴于转轮表面多为不规则的空间曲面,对其采用四面体非结构化网格进行划分。定子与转子之间的相互影响不可忽略,基于此,采用滑移网格模型[17]。3叶片转轮计算区域的网格划分见图4。

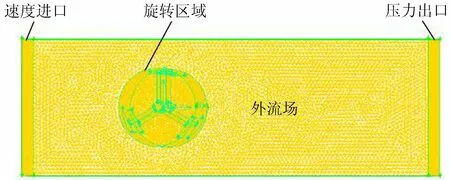
图4 计算区域网格划分

3 计算结果分析

3.1 周期内流场压力分布

图5为来流速度v=1.5 m/s、转速n=13.38 r/min工况下,不同叶片数水轮机在相同时刻的转轮流场截面云图,可以明显看出转轮在相同时刻时,随着叶片数不同,周围压力发生很大的变化,靠近来流方向转轮左侧盘面区域流场压力大于转轮右侧盘面区域,当转轮转动,直叶片处在左侧盘面区域特别是180°相位角附近时,叶片压力面压力远远大于吸力面压力。

从图5还可以看出,当叶片在180°相位角附近区域时,叶片吸力面压力很小,甚至小于转轮内部压力,当叶片转动到右侧盘面区域时,压力面压力往往小于吸力面压力;特别是叶片前缘尖端附近区域,来流由于受到叶片的阻碍作用,流速很小,导致叶片前缘小区域压力很大,直叶片在左侧盘面区域时,前缘压力极大区域出现在叶片压力面,不过当直叶片在右侧盘面区域时,压力极大区域出现在叶片吸力面。

3.2 不同叶片数转轮动力扭矩特性

图6为来流速度v=1.5 m/s、转速n=13.38 r/min工况下,不同叶片数的转轮单叶片扭矩曲线在一个转动周期内的分布规律,直叶片在左侧盘面靠近来流最前端180°相位角附近时出力最大,同时从图6可以看出叶片数对垂直轴潮流水轮机的出力影响很大,随着叶片数增多,单叶片周期内输出扭矩最大值减小,转轮右侧盘面区域叶片出力为负值,做负功阻碍水轮机转轮转动。

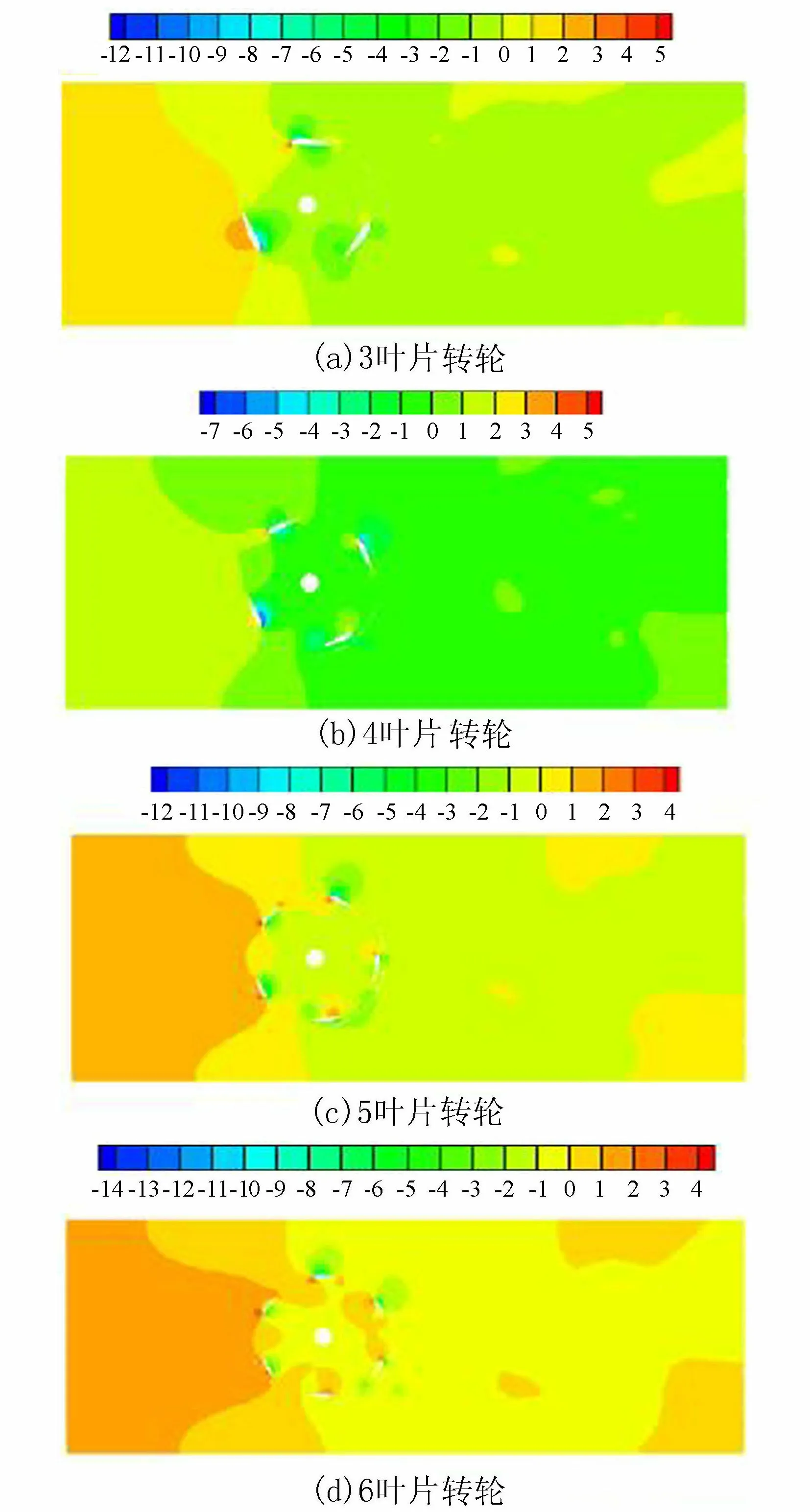
图5 流场压力云图(单位:kPa)

图6 单叶片输出扭矩

图7为不同叶片数整体转轮在一个周期内的扭矩输出曲线,呈规律性分布,3叶片的转轮周期内出现3次波峰3次波谷,4叶片的转轮出现4次波峰4次波谷,5叶片、6叶片的转轮也有同样的规律;在相同工况以及保持同样转轮密实度的条件下,直叶H型潮流水轮机转轮叶片数越多,输出扭矩最大值越小,但是输出扭矩最小值却没有类似的规律,3叶片转轮的输出扭矩最小值最小,6叶片转轮输出扭矩最小值稍大,4叶片和5叶片转轮输出扭矩最小值相当,为最大。从图7还可以看出,叶片数超过一定值,如大于4时,转轮输出扭矩值减小得很快,呈现骤降的趋势,叶片数越多,转轮输出扭矩值周期性波动越小。

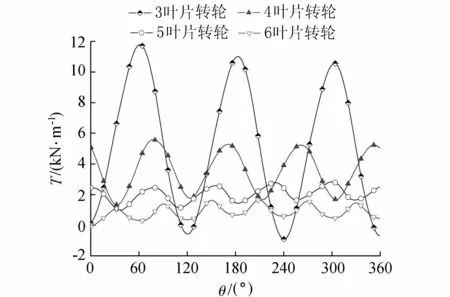
图7 转轮输出扭矩

3.3 获能系数计算

获能系数计算公式为

(4)

式中:T为输出扭矩；ω为旋转角速度;v为来流速度;D1为水轮机外径;h为水轮机叶片高度。由式(4)可计算得到不同叶片数下转轮各种工况的获能系数曲线如图8所示。

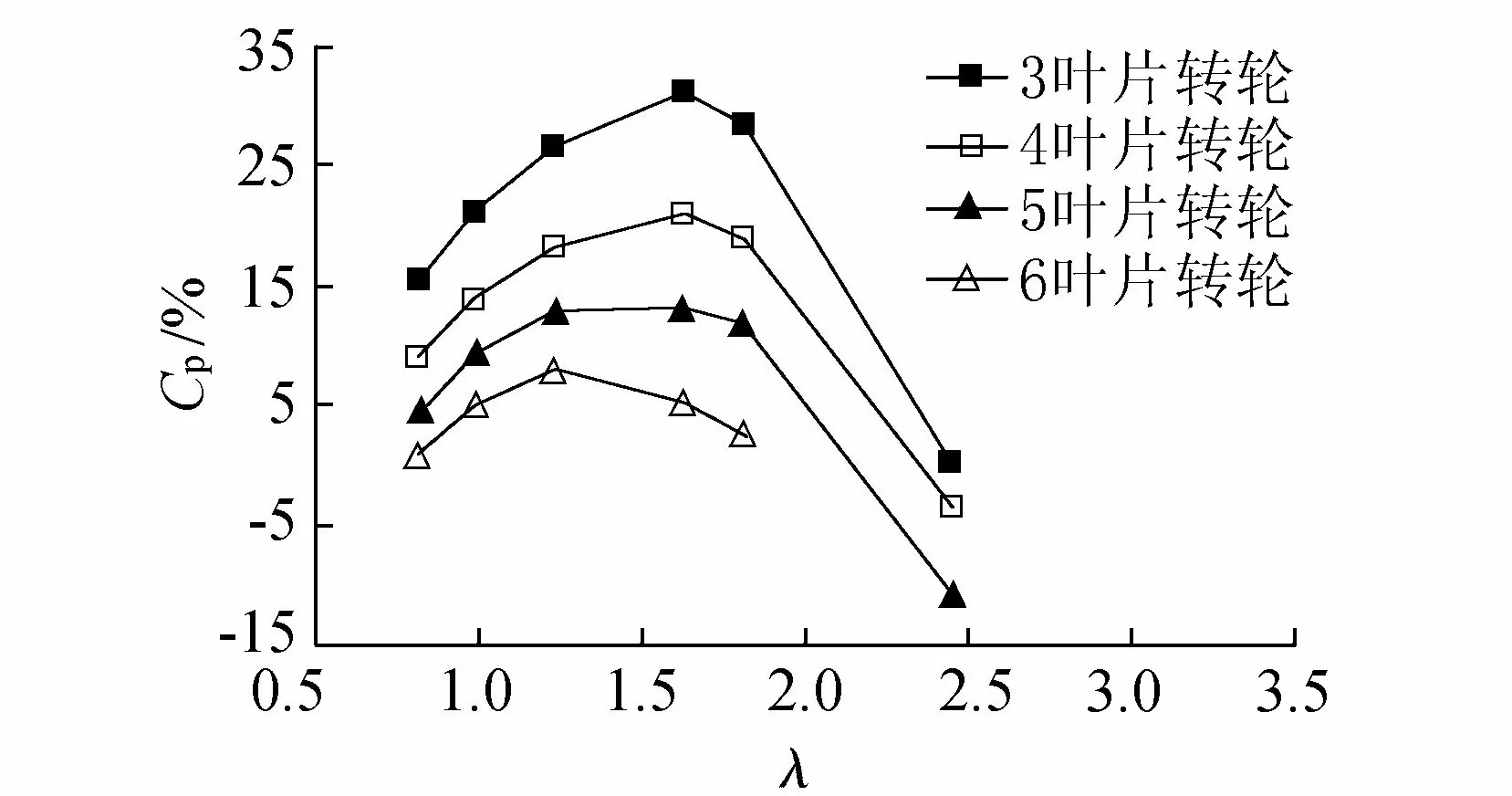
图8 转轮获能系数曲线

从图8可以看出，同一翼型相同工况,密实度相同条件下,转轮的获能系数随着叶片数增多越来越低,当转轮叶片数为3,叶尖速比λ=1.63时,直叶H型潮流水轮机最高获能系数为31.21%。获能利用的高效区在叶尖速比λ为1～2之间,当转轮叶片数为3、4及5时,最佳叶尖速比为1.63,叶片数为6时,水轮机最佳叶尖速比为1.24;同时从图8还可以看出,当叶尖速比超过某一极限值,直叶H型潮流水轮机输出扭矩为负值,阻碍转轮转动,转轮获能系数为负值,此时不做正功,转轮叶片数不同,这一极限值也有所不同,3叶片转轮为2.48,4叶片转轮为2.37,5叶片转轮为2.12,根据趋势6叶片转轮近似为1.87。

4 结论

a. 直叶H型潮流水轮机转轮旋转时,叶片所处相位角位置不同,过流流场有不同的压力分布,靠近来流方向转轮左侧盘面区域流场压力大于转轮右侧盘面区域,转轮直叶片在180°相位角附近区域时,叶片压力面压力远远大于吸力面压力。

b. 不同叶片数的直叶H型潮流水轮机在同一工况下运行时,输出扭矩值呈周期性分布,叶片数越多,输出扭矩值越小,输出扭矩值周期性波动越小。

c. 直叶H型潮流水轮机获能的高效区在叶尖速比为1～2之间,当转轮叶片数为3、叶尖速比为1.63时,直叶H型潮流水轮机最高获能系数为31.21%。

[1] 魏东泽,吴国荣,郭欣,等.潮流能开发技术研究进展[J].可再生能源,2014,32(7):1067-1074.(WEI Dongze,WU Guorong,GUO Xin,et al.Research progress in exploration technology of tidal current energy[J].Renewable Energy Resources, 2014,32(7):1067-1074.(in Chinese))

[2] 戴庆忠.潮流能发电及潮流能发电装置[J].东方电机,2010(2):51-66.(DAI Qingzhong.Generate using the tidal current energy and the generation device[J].Oriental Motor,2010(2):51-66.(in Chinese))

[3] BURGER M,REID N.Hydrodynamic array: US8841790B1[P]. 2013-03-19.

[4] 戴军, 单忠德, 王西峰,等.潮流水轮机的研究进展[J].可再生能源,2010,28(4):130-133.(DAI Jun,SHAN Zhongde, WANG Xifeng,et al.Research status of tidal current turbine[J].Renewable Energy Resources,2010,28(4):130-133.(in Chinese))[5] 张亮, 李志川, 张学伟,等.垂直轴潮流能水轮机研究与利用现状[J].应用能源技术,2011(9):1-7.(ZHANG Liang,LI Zhichuan,ZHANG Xuewei,et al.The status of research and application of vertical axis tidal turbine[J].Applied Energy Technology,2011(9):1-7.(in Chinese))

[6] 张亮,李新仲,耿敬,等.潮流能研究现状2013[J].新能源进展,2013,1(1):53-68.(ZHANG Liang,LI Xinzhong,GENG Jing,et al.Tidal current energy update 2013[J].Advances in new and Renewable Energy,2013, 1(1):53-68.(in Chinese))

[7] 王树杰,鹿兰帅,李冬,等.潮流发电帆翼式柔性叶片水轮机实验研究[J].海洋工程,2009,27(1):83-89.(WANG Shujie,LU Lanshuai,LI Dong,et al.Experimental investigation on sail-winged flexible blade turbine[J].The Ocean Engineering, 2009,27(1):83-89.(in Chinese))

[8] 李凤来,张亮,张洪雨,等.70 kW潮流电站水轮机研究[R].哈尔滨:哈尔滨工程大学,2002.

[9] 盛其虎,罗庆杰,张亮.40 kW潮流电站载体设计[C]中国可再生能源学会海洋能专业学术委员会成立大会暨第一届学术讨论会论文集.杭州:中国可再生能源学会海洋能专业学术委员会,2008:159-168.

[10] 张楠.漂浮式潮流电站叶轮与锚泊系统设计研究[D].哈尔滨:哈尔滨工程大学,2011.

[11] 张亮,孙科,罗庆杰.潮流水轮机导流罩的水动力设计[J].哈尔滨工程大学学报,2007,28(7):734-737.(ZHANG Liang,SUN Ke,LUO Qingjie.Hydrodynamic design of diversion cover for a tidal-stream hydro turbine[J].Journal of Harb in Engineering University,2007,28(7):734-737.(in Chinese))

[12] 罗庆杰,张亮,孙科.UDF控制滑移网格方法在摆线式直叶水轮机性能预报中的应用[C]中国可再生能源学会海洋能专业学术委员会成立大会暨第一届学术讨论会文集.杭州:中国可再生能源学会海洋能专业学术委员会,2008:124-132.

[13] 付士凤,李龙,邓力,等.基于滑移网格的垂直轴潮流水轮机的三维数值模拟[J].水电能源科学,2014,32(7): 140-143.(FU Shifeng,LI Long,DENG Li,et al.CFD simulation of vertical axis tidal turbine based on sliding mesh[J].Water Resources and Power,2014,32(7):140-143.(in Chinese))

[14] 李允武.海洋能源开发[M].北京:海洋出版社,2008.

[15] 胡玉仙.基于FLUENT软件的泵站进出水流道流动模拟研究[D].武汉:武汉大学,2004.

[16] 周俊波.Fluent 6.3流场分析：从入门到精通[M].北京:机械工业出版社,2012.

[17] 韩占忠,王敬,兰小平.FLUENT流体工程仿真计算实例与应用[M].北京:北京理工大学出版社,2008.

Three-dimensional numerical simulation of H-type straight-blade tidal turbine

FU Shifeng1,ZHENG Yuan1,LIANG Xiaoling2,KAN Kan1,CHEN Huixiang1,YANG Chunxia1

(1.CollegeofWaterConservancyandHydropowerEngineering,HohaiUniversity,Nanjing210098,China; 2.HohaiUniversityWentianCollege,Maanshan243031,China)

In order to explore the factors influencing the hydrodynamic performance of an H-type straight-blade tidal turbine, based on theoretical analysis, a three-dimensional model of an H-type straight-blade tidal turbine was established using large-scale modeling software UG, and three-dimensional numerical simulations were carried out using the Fluent software and the sliding mesh method. Under the conditions with the same airfoil type of H-type turbine blade and the same turbine solidity, the hydrodynamic performance of the tidal turbine was analyzed by changing the number of runner blades and inflow velocity. The results show that the number of blades has a significant effect on the hydrodynamic performance of the H-type straight-blade tidal turbine. The greater the number of blades, the smaller the output torque is. When the number of blades is three and the tip speed ratio is 1.63, the highest turbine power coefficient is 31.21%.

tidal turbine; straight blade; hydrofoil type; hydrodynamic performance; numerical simulation