基于DEM的碎屑流运动特性数值模拟

赵 川,付成华

(西华大学能源与动力工程学院,四川 成都 610039)

基于DEM的碎屑流运动特性数值模拟

赵 川,付成华

(西华大学能源与动力工程学院,四川 成都 610039)

采用颗粒离散元法建立了碎屑流三维数值模型,分别从整体和局部对碎屑流运动特性进行深入分析。结果表明:碎屑流的运动过程可分为启动加速、高速滑动和减速堆积3个阶段;边坡底面平整时,堆积体中大颗粒堆积在表面,而细小颗粒位于中下部位;碎屑流运动速度和能量损失受颗粒间的接触碰撞影响大;碎屑流不同部位运动速度最大值相同,达到速度峰值的时间与颗粒的初始水平位置有关,与深度无关;堆积体分区明显,堆积体中的颗粒按初始水平位置依次排布;坡脚位置堆积深度最大,往两侧逐渐减小;碎屑流在运动初期和末期横向运动明显,扩大了灾害影响范围。

碎屑流;三维颗粒离散元法;碰撞接触;堆积体;数值试验

碎屑流是一种滑坡岩体在初始状态或者高速运动过程中转化为碎屑物质的运动形式,其某些运动特性与流体相似。碎屑流是一种常见的自然灾害,有运动速度快、携带岩体量大和破坏力强等特点,对人民生命财产安全构成巨大威胁。我国地形条件复杂,高山丘陵广泛分布,发生地质灾害的频率很高,尤其是我国西南地区在遭受了汶川地震后,边坡表层岩体破碎严重,更是碎屑流灾害的高发地带[1]。黄润秋[2]分析了20世纪以来中国的大型滑坡,将其分为岩质滑坡、土层滑坡和松散堆积层滑坡3类。本文研究的碎屑流不考虑颗粒单元间的黏结作用,属于松散堆积层滑坡。

20世纪以来,国内外学者对颗粒碎屑物质进行了大量研究，《Science》于2005年把颗粒物质列为100个科学难题之一[3-4];Iverson等[5]基于复杂的三维地形,对沙粒崩塌(granular avalanche)进行了室内物理实验,并采用连续介质模型进行模拟,模拟结果与实验结果基本吻合;Hussin等[6]以MassMov2D为工具,通过反分析确定了某滑坡带的计算参数,对潜在的滑坡进行了预测;王玉峰等[7]对汶川地震触发的高速远程碎屑流堆积反粒序特征进行了分析,揭示了碎屑流堆积体内部所特有的堆积规律;张明等[8]对目前碎屑流的研究成果进行了系统的归纳和总结。总的看来,已有的碎屑流研究对象主要针对室内小尺寸模型或已经发生的具体滑坡。具体的滑坡案例受地形条件影响大,室内模型难以反映真实高速碎屑流的某些运动特性,其研究结论难以反映一般规律[9-12]。

为了解决上述碎屑流研究存在的问题,本文采用三维颗粒离散元法(discrete element method，DEM)建立了标准的碎屑流数值模型,选用含有棱角的颗粒单元,并通过漏斗模型试验标定计算参数,对碎屑流运动特性进行了深入分析探讨。

1 碎屑流数值模型建立及参数选取

1.1 离散元模型构建

碎屑流数值模型主要由碎屑堆积槽、滑动面和堆积面组成。滑动面和堆积面构成一个边坡系统，坡高为10 m,坡比为1∶2,堆积面长为10 m;碎屑堆积槽用于放置颗粒物质,槽外形为三棱柱体,尺寸为1.5 m×3 m×5 m,如图1所示。

图1 碎屑流离散元模型尺寸(单位:m)

由于真实岩体碎屑外形并非标准球体,而是含有一定棱角的球体,因此模型试验中构建了含有棱角的颗粒单元,如图2所示,其中图2(a)为真实碎屑流块体,图2(b)为构建的离散元块体。颗粒大小按高斯分布随机生成,直至充满堆积槽,颗粒总数为3 707,总填充体积22.5 m3,最终颗粒模型试样如图3所示。

图2 数值计算颗粒单元外形

图3 碎屑流离散元模型

滑坡碎屑流运动过程中,岩块之间存在大量的碰撞和接触,为准确描述DEM中颗粒单元运动过程的力学行为,计算采用Hertz-Mindlin无滑动接触模型,主要包括法向力Fn、法向阻尼力Fnd、切向力Ft和切向阻尼力Ftd4个参数,计算公式[13-14]如下:

(1)

(2)

Ft=-Stδt

(3)

(4)

式中:R*为等效颗粒半径,m;Y*为等效杨氏模量,Pa;δn、δt分别为两个颗粒接触面法向与切向重叠量,m;m*为等效质量,kg;vn、vt分别为两个颗粒接触面法向和切向相对速度,m/s;β为阻尼力系数;Sn、St分别为两个颗粒接触面法向与切向刚度。

1.2 数值计算参数标定

碎屑流的运动受摩擦系数的影响很大,为校核相关摩擦系数,对试验选用的颗粒采用漏斗模型试验进行标定,如图4所示。由于本试验中碎屑颗粒间不存在黏结力,其天然休止角即为松散堆积体的内摩擦角φ。数值试验中滑动面为平面,为模拟边坡表面覆盖的松散堆积层[15],基底摩擦系数取0.42,颗粒间摩擦系数取0.4。具体方法是首先设置好基底摩擦系数和颗粒间摩擦系数,通过不断调整滚动摩擦系数重复计算,将堆积体的天然休止角为22°(arctan 0.4=arctanH/R=21.8°,其中H为堆积体中心高度,R为堆积体底半径)时所采用的参数作为碎屑流模型的参数,最终得到的计算参数见表1。

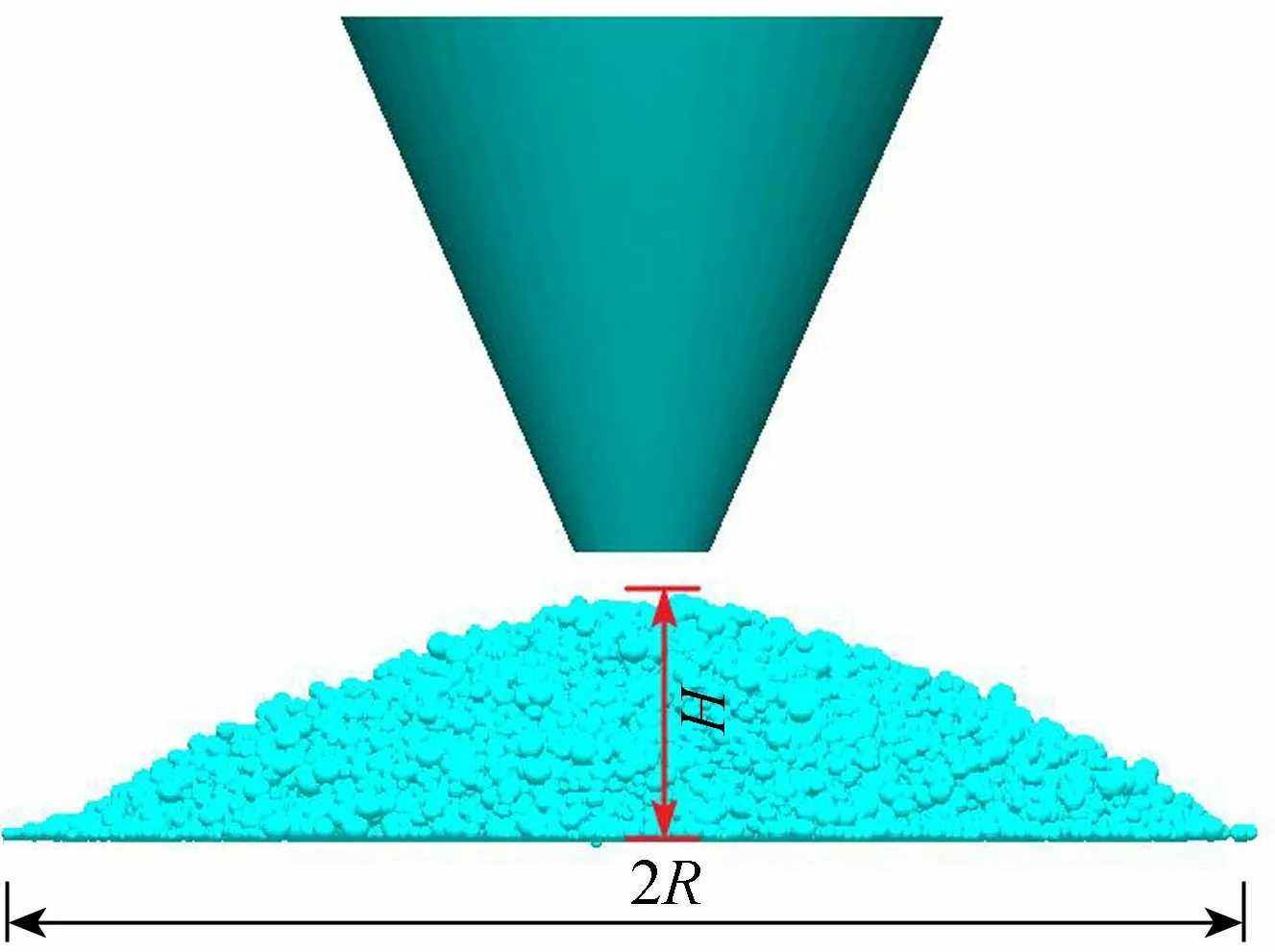
图4 离散元颗粒漏斗数值模型试验

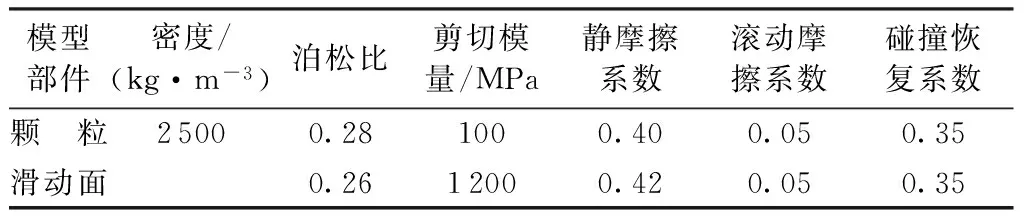
表1 DEM模型相关参数取值

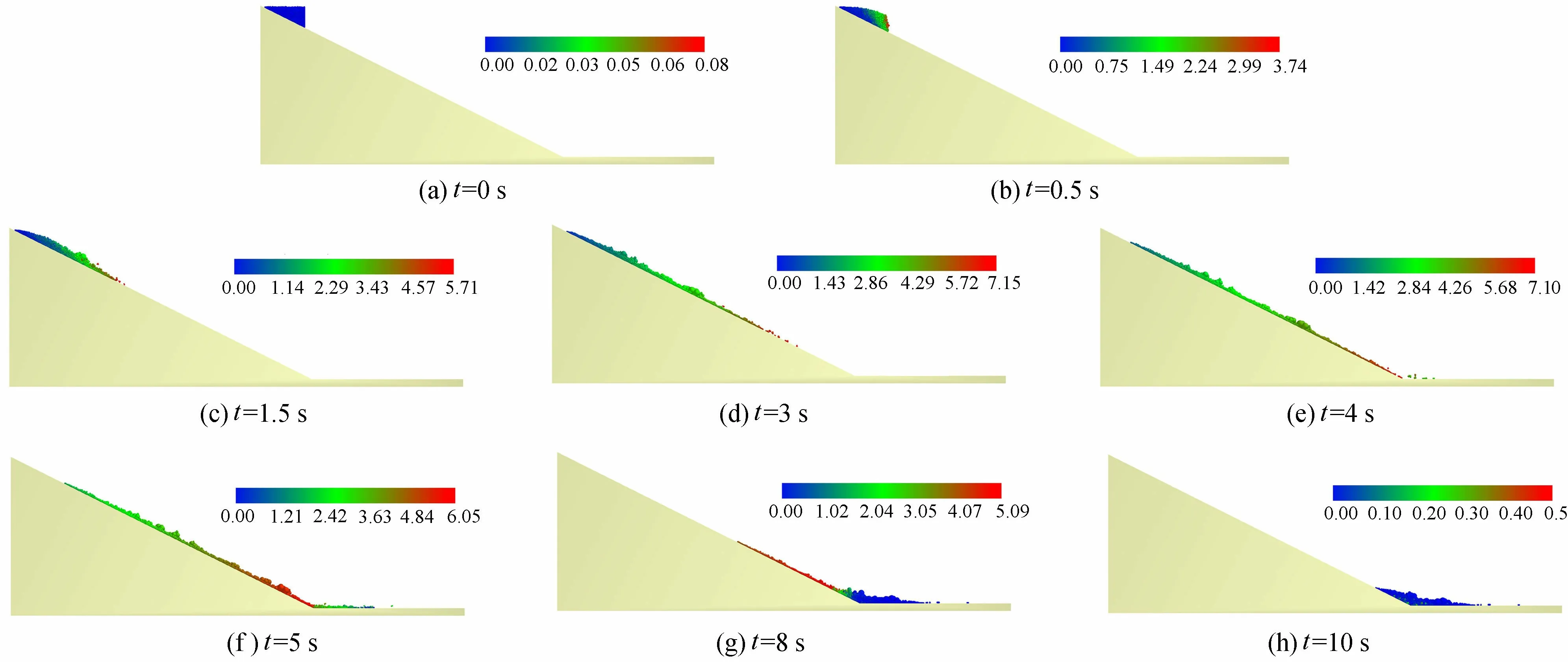
图5 不同时刻碎屑流运动速度分布(单位：m/s)

2 数值试验结果及分析

2.1 整体运动特性

为分析岩体碎屑流不同时刻的运动状态,图5给出了碎屑流的运动速度分布。在时间t=0 s时,撤掉试样前端挡板,在重力作用下,颗粒开始沿着坡面向下运动。由于颗粒并不是标准的球形颗粒,而是含有棱角的颗粒单元,所以整个运动过程中主要以平面滑动为主,仅在颗粒流表面存在滚动现象。运动过程中,前端颗粒由于所受约束小,运动速度较大,最大颗粒速度超过7 m/s。t=4 s时,前端颗粒运动到堆积面,并与底面发生碰撞,动能损失较大,速度逐渐减小,并堆积在坡脚位置。最终形成的堆积角在10°左右,仅为初始坡角26.6°的38%。

图6为整个运动过程颗粒物质平均速度随时间的变化,10 s时碎屑的平均速度仅为0.002 m/s,运动基本停止。根据曲线变化趋势,可将碎屑流的运动过程划分为启动加速、高速滑动和减速堆积3个运动阶段,分别对应的时间段为0～4 s、4～6 s和6～10 s,加速和减速阶段所用的时间大体相当,均占总耗时的40%左右,而高速滑动仅占总耗时的20%。

图6 碎屑流平均速度的变化过程

另外,从最后的堆积体颗粒分布可以发现,大颗粒位于堆积体表面,细小颗粒位于堆积体中下部位。究其原因,是由于在运动过程中,颗粒间相互碰撞摩擦,颗粒间存在一定大小的空隙,细小颗粒沿着空隙下落到堆积体底部,从而形成大颗粒物质在表面、细小颗粒在中下部的现象,这与实际碎屑流形成的堆积序列相符。

模拟时不考虑岩体间的黏结力,仅考虑相互碰撞作用。图7为碎屑流运动过程中颗粒单元相互接触数量随时间的变化,初始时刻堆积较为紧密,总的接触数量大约有11 500;随着运动速度的增大接触数量逐渐减小,在t=5.4 时接触数量减小到最小值1 841,说明此时颗粒最为稀疏,颗粒间相互作用最少;此后随着颗粒流前缘堆积体逐渐形成,接触数量又逐渐增加,最后可达13 500左右,略大于初始时刻的数量。对比图6和图7可见,碎屑流的平均速度随时间的变化曲线与单元接触数量随时间的变化曲线的变化趋势正好相反,且速度的最大值正好对应接触数的最小值,均发生在t=5.4 s时,说明颗粒越稀疏,运动速度越大,颗粒越密集意味着更多的碰撞,而碰撞将导致碎屑流内部能量大量耗散,故运动速度也随之减小。

图7 颗粒单元接触数量的变化过程

图8为单元的运动迹线和速度,可以发现大部分单元的速度分布基本是连续变化的,表现出一定的流体性质,但少数表面不连续的红色线条显示出存在颗粒单元在某个时段内脱离碎屑流运动,而单独以较大的速度在表面发生跳动,这是由于表面部分高速运动的颗粒之间发生偏心碰撞和回弹造成的。

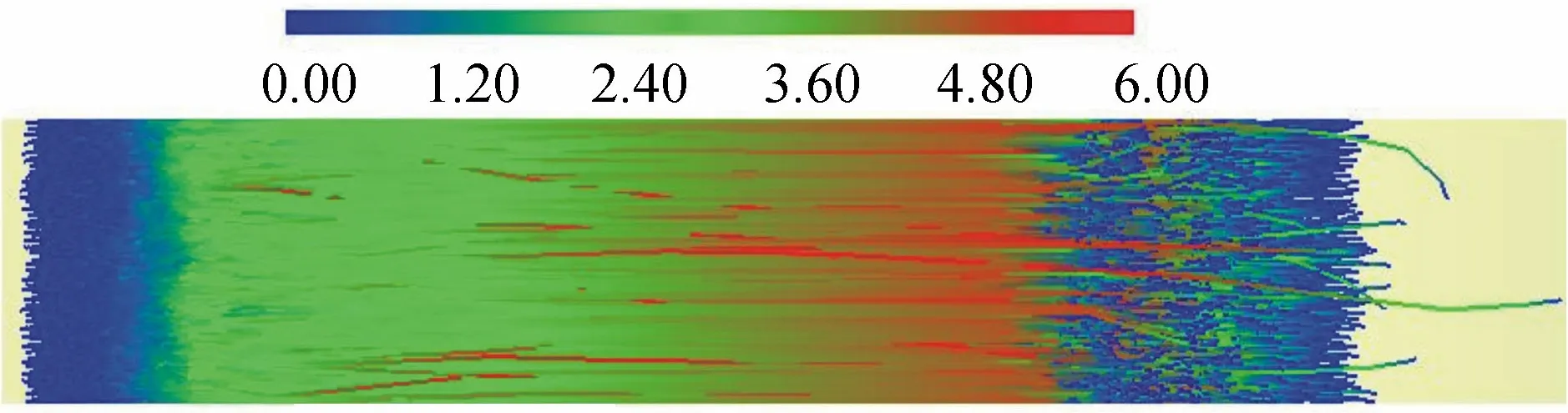
图8 碎屑流DEM模型单元运动迹线及速度(单位:m/s)

2.2 局部运动特性分析

为分析碎屑流不同部位在运动过程中的差异,将模型试样分成5个区域,每部分颗粒总数占总颗粒数的20%左右,并分别编号A、B、C、D、E,如图9所示,其中A区代表后部,B区代表中上部,C区代表中下部,D区代表前端上部,E区代表前端下部。图10为5个区域内颗粒的运动速度随时间的变化过程,可以发现,位于前端的C和E区的颗粒最先启动,在前0.5 s内,曲线斜率很大,说明速度增长很

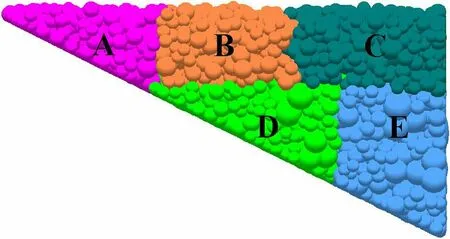
图9 颗粒分区

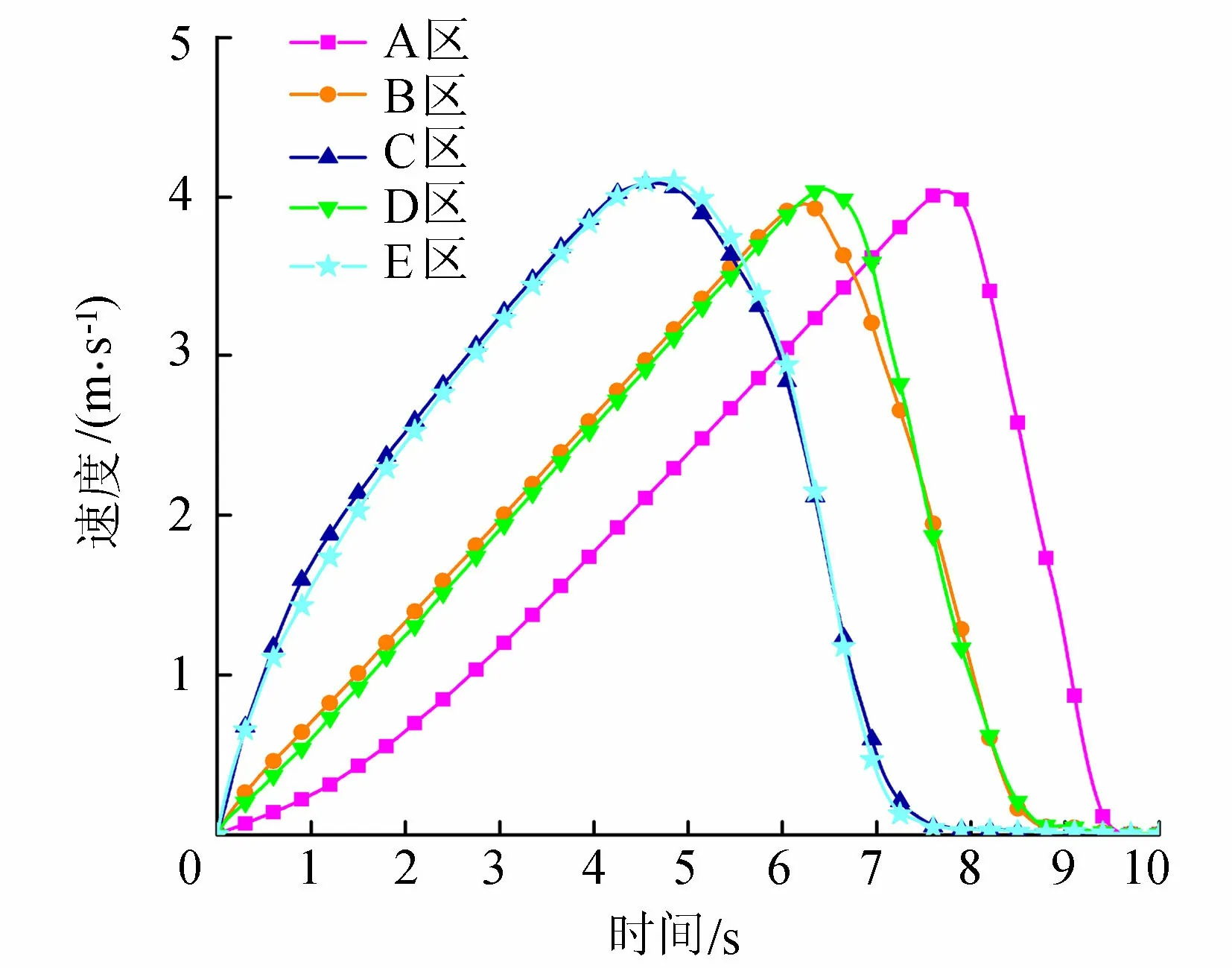
图10 不同分区颗粒的运动速度

快,这是由于前端颗粒在初始时刻存在掉落现象,随后曲线斜率保持稳定,在t=4.5 s时速度达到最大值;而位于中部的B和D区颗粒启动稍晚,在加速运动过程中,速度增长保持稳定,在t=6.5 s左右速度达到峰值;位于最后端的A区则最后启动,且初始时刻速度增加幅度不大,这是因为中部的B区和D区颗粒阻挡和延迟了A区颗粒的运动,随后速度逐渐增加,并在t=8 s时速度达到最大值。综合分析可见,5个区域的颗粒速度在不同时刻达到最大值,且最大值基本相同,约为4.5 m/s;B区颗粒速度稍小,为4.4 m/s。

图11为5个区域内颗粒在水平方向x、竖直方向y、横向z的运动速度分量,可以发现x方向的速度最大,最大峰值速度约4 m/s;y方向的速度次之,最大速度约2 m/s;z方向的速度最小,最大也仅有0.04 m/s。各部分颗粒的x和y方向速度几乎同时达到最大值,且曲线变化趋势也基本相同,其中C和E区颗粒在前0.5 s内y方向速度快速增大,这是颗粒突然释放且前缘部分受到阻力很小造成的(图11(b))。z方向颗粒运动速度一直较小,具体分析曲线变化趋势可以发现:在碎屑流运动初期,位于前缘的C和E区颗粒横向运动较为明显;运动中期各部分颗粒z方向运动速度均很小,此阶段内颗粒堆积密度最小,相互之间的碰撞挤压也最少;在最后的堆积期间,A、C和D区的颗粒横向运动速度相对大一些。总体来说,在运动初期和最后堆积期,颗粒沿运动方向速度较小时,z方向的速度相对较大;而当颗粒沿运动方向高速运动时,z方向速度相对较小(图11(c))。

图12为碎屑流最终的堆积状态,A区颗粒完全堆积在坡面上,B和D区大部分堆积在坡面上,极少部分堆积在坡脚以下; C和E区的颗粒完全堆积在底面上,堆积长度较大,越往前堆积厚度越小;坡脚位置的堆积厚度最大,最大堆积厚度可达1 m。

图12 碎屑流最终堆积状态

3 结 论

a. 根据碎屑流速度时间曲线,可将其运动过程划分为3个运动阶段:启动加速段、高速滑动段和减速堆积段。

b. 碎屑流在平整坡面上运动时,存在大量接触和碰撞,小颗粒不断通过空隙向下运动,最终造成了明显的堆积分布序列:大颗粒位于堆积体表面,小颗粒位于堆积体底部,在坡脚位置堆积深度最大;碎屑流的速度随时间的变化曲线与单元接触数量随时间变化曲线的变化趋势恰好相反,且速度的最大值正好对应接触数量的最小值。

c. 不同区域内颗粒速度最大值基本相同,但达到最大值的时刻有所不同,这与颗粒的初始水平位置相关,而与其深度无关;各区域内颗粒水平和竖直方向运动速度较大,且变化趋势基本同步,而横向速度相对较小;堆积体分区明显,堆积体中的颗粒按初始水平位置依次排布。

d. 碎屑流沿运动方向高速运动时,横向速度很小;在碎屑流运动初期和堆积末期,水平和竖直方向运动速度较小,横向速度较大,碎屑流横向运动更为明显,扩大了灾害横向影响范围。

[1] 郑颖人,陈祖煜,王恭先,等.边坡与滑坡工程治理[M].北京:人民交通出版社,2007.

[2] 黄润秋.20世纪以来中国的大型滑坡及其发生机制[J].岩石力学与工程学报,2007,26(3):433-454.(HUANG Runqiu.Large-scale landslides and their sliding mechanisms in China since the 20th century[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(3): 433-433.(in Chinese))

[3] HEWITT K.Catastrophic landslide deposits in the Karakoram Himalaya[J].Science,1988,242:64-67.

[4] 孙其诚,王光谦.颗粒物质力学导论[M].北京:科学出版社,2009.

[5] IVERSON R M,LOGAN M,DENLINGER R P.Granular avalanches across irregular three-dimensional terrain: 2.experimental tests[J].Journal of Geophysical Research: Earth Surface,2004,109(1):337-357.

[6] HUSSIN H Y,CIUREAN R,FRIGERIO S,et al.Assessing the effect of mitigation measures on landslide hazard using 2D numerical runout modeling[J].Landslide Science for a Safer Geoenvironment,2014,2(6):679-684.

[7] 王玉峰,程谦恭,朱圻.汶川地震触发高速远程滑坡-碎屑流堆积反粒序特征及机制分析[J].岩石力学与工程学报,2012,31(6): 1089-1106.(WANG Yufeng,CHENG Qiangong,ZHU Qi.Inverse grading analysis of deposit from rock avalanches triggered by Wenchuan Earthquake[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(6): 1089-1106.(in Chinese))

[8] 张明,殷跃平,吴树仁,等.高速远程碎屑流运动机理研究发展现状与展望[J].工程地质学报,2010,18(6):805-817.(ZHANG Ming,YIN Yueping,WU Shuren,et al.Development status and prospects of studies on kinematics of long runout rock avalanches[J].Journal of Engineering Geology,2010,18(6): 805-817.(in Chinese))

[9] BANTON J,VILLARD P,JONGMANS D,et al.Two-dimensional discrete element models of debris avalanches: parameterization and the reproducibility of experimental results[J].Journal of Geophysical Research: Earth Surface,2009,114(4):60-71.

[10] LO Chaiming,LIN Minglang,TANG Chaolung,et al.A kinematic model of the Hsiaolin landslide calibrated to the morphology of the landslide deposit[J].Engineering Geology,2011,123(1):22-39.

[11] HARALD T,WANG Y,CHIOU M C,et al.Flow-obstacle interaction in rapid granular avalanches: DEM simulation and comparison with experiment[J].Granular Matter,2009,11(4):209-220.

[12] 毕钰璋,付跃升,何思明,等.牛眠沟地震滑坡碎屑化全过程离散元模拟[J].中国地质灾害与防治学报,2015,26(3):17-25.(BI Yuzhang,FU Yuesheng,HE Siming,et al.Simulation of the whole process of Niumiangou creek rock avalanche triggered by the earthquake using a distinct element method[J].The Chinese Journal of Geological Hazard and Control,2015,26(3):17-25.(in Chinese))

[13] 徐泳,孙其诚,张凌,等.颗粒离散法研究进展[J].力学进展,2003,33(2):251-260.(XU Yong,SUN Qicheng,ZHANG Ling,et al.Advances in discrete element methods for particulate materials[J].Advances in Mechanics,2003,33 (2): 251-260.(in Chinese))

[14] 王国强,郝万军,王继新.离散单元法及其在EDEM上的实践[M].西安: 西北工业大学出版社,2010.

[15] 钱家欢,殷宗泽.土工原理与计算[M].2版.北京:中国水利水电出版社,1996.

Numerical simulation of movement characteristics of debris flow based on DEM

ZHAO Chuan, FU Chenghua

(SchoolofEnergyandPowerEngineering,XihuaUniversity,Chengdu610039,China)

A three-dimensional numerical model for debris flow was established with the particle discrete element method (DEM), and the movement characteristics of debris flow were analyzed from the full and local aspects. The results show that the movement process of debris flow can be divided into three stages, including starting acceleration, high-speed sliding, and reduced-speed deposit. When the bottom of the slope is flat, large particles are found on the surface of the deposition body, but small particles are in the middle and low areas. The velocity and energy loss of debris flow is significantly influenced by the contacts and collisions between particles. The maximum speeds of different parts of the debris flow are almost the same, and the time required to reach the speed peak is related to the initially horizontal position of particles, but not related to the deposit depth. Area division is distinct in the deposition body, and the particles of the deposition body are arranged according to their initially horizontal positions. The maximum deposit height is at the slope toe, and the deposit height gradually decreases towards both sides. Significant lateral movement occurs in the debris flow in the early and late stages, which can expand the scope of a disaster.

debris flow； 3-D particle discrete element； numerical experiment； contact collision； deposition body

西华大学流体及动力机械教育部重点实验室(重点研究基地)开放课题(szjj2015-039)

赵川(1989—),男,硕士研究生,主要从事岩土工程稳定性研究。E-mail:zhaochuanvip@163.com

付成华(1978—),女,副教授,博士,主要从事水利水电工程研究。E-mail:fuchh_xhu@163.com

10.3880/j.issn.1006-7647.2017.02.008

P642.21

：A

：1006-7647(2017)02-0043-05

2016-02-26 编辑：郑孝宇)