单元嵌套网格产汇流理论

芮孝芳

(河海大学水文水资源学院，江苏 南京 210098)

单元嵌套网格产汇流理论

芮孝芳

(河海大学水文水资源学院，江苏 南京 210098)

凭借“大数据”可以精细刻画降雨空间分布和下垫面空间变异性的优势，提出了“大数据”背景下考虑降雨空间分布和下垫面空间变异性对流域产汇流影响的计算方法，即单元嵌套网格剖分流域的方法。通过引入“网格水滴”的概念揭示了流域瞬时单位线的物理本质，对由Rodriguez-Iturbe和Valdes所提出R-V地貌瞬时单位线理论进行补充，分析了等流时线法和单位线法的局限性，提出的单元嵌套网格产汇理论既克服了等流时线法和单位线法的缺点，也吸取了它们的优点，为在“大数据”支撑下统一等流时线和单位线法提供了可行性。

流域基本单元；网格水滴；流域产汇流；大数据；流域地貌瞬时单位线；等流时线

早在20世纪七八十年代，一些水文学家就曾试图借助普适性物理定律(如质量守恒定律、能量守恒定律、Newton力学定律等)，以及一些水文学本构关系(如Darcy公式、Manning公式、水位-流量关系曲线等)，建立描述流域产汇流的微分方程，再考虑初始条件和边界条件构成定解问题，最后解出具有一定时空分布的降雨所形成的流域出口断面流量过程。1970年《动力水文学》一书的出版[1]和1986年SHE模型[2]的出现就是这方面的代表性事件。动力水文学试图将流域产汇流问题纳入牛顿力学可以解决的问题之列，而SHE模型则是该思路的一次大胆尝试。

SHE模型将流域产汇流看作连续介质运动，无论是植物截留、蒸散发、下渗，还是坡面水流、地下水流、河网水流，甚至冰雪增消等都可用相应的连续性方程和能量或动力方程加以描述。由于这些微分方程原本都是非线性的，加之相互之间存在着复杂的耦合关系，以致SHE模型的构建者们费了九牛二虎之力才对位于英国威尔士中部仅10.55 km2的Wye河流域得出了流域产汇流的数值解。令人遗憾的是解的精度很不理想，甚至低于概念性模型的计算精度。高难度的求解并未换来理想的精度，使得迄今尚未发现SHE模型的实际应用。究其原因，可能是因为在建立描述现象的微分方程时使用了不合理的假设或者作了不合理的概化，也可能是因为数学方法求解精度不够高或稳定性不够好，但更主要的也许是无法客观精细地考虑降雨和下垫面空间变异性对流域产汇流的影响。

受“大数据”[3]的启迪,笔者认为，对于十分复杂的流域产汇流问题，似乎不应该将解决问题的希望唯一地寄托于建立和求解微分方程，而凭借可靠、密集的大数据也不失为一种可供选择的描述和揭示流域产汇流规律的途径。本文尝试对后一种途径展开讨论，定名为“单元嵌套网格产汇流理论”。

1 流域的剖分

为了客观精细地考虑降雨和下垫面空间分布对流域产汇流的影响，必须对流域进行剖分。早在20世纪60年代，就出现了按雨量站分布或按流域内部分水线剖分流域的方法[4]。1968年，Schultz在将雷达测雨应用于产汇流分析时，首次提出了用网格剖分流域的方法[5]。除此以外，也有提出按等雨量线或等流时线或特征河长剖分流域。在对流域产汇流现象的不断认识和探索过程中，为着不同目的提出不同的流域剖分方法是很正常的，但当人们将思路逐步理清后，就会在分析前人所提出方法的优、缺点基础上，通过取长补短，提出更为合理的流域剖分方法。单元嵌套网格剖分法就是在这样的背景下提出来的。

流域由坡面和水系组成。水系由河流交汇而成。河流与河流之间必有分水线相隔。因此，对一个流域按其内部分水线可划分成一些不嵌套的较小流域，对这些较小的流域，又可按其各自的内部分水线划分成不嵌套的更小流域。这样不断地剖分下去，最终无法再按分水线剖分下去的“最小流域”称为“流域基本单元”[6]。

从地形图或数字高程模型(DEM)提取流域基本单元显然受到地形图比例或DEM分辨率的影响，一般来说，流域基本单元仍有几平方千米到十几平方千米不等，这对客观、精细地考虑降雨空间分布和下垫面空间变异性对流域产汇流的影响仍有困难。为此，对流域基本单元还要再进行网格剖分。一个流域经过这样两次剖分处理后，就可表达为由水系连接的若干个嵌套网格的流域基本单元的串并联结构，如图1所示。

图1 单元嵌套网格剖分

单元嵌套网格剖分法吸取了分水线剖分法和网格剖分的优点，因此是一种既便于从理论上分析水滴运动，又与“大数据”科学思维方式处理流域产汇流问题相匹配的流域剖分方法。

水滴在流域坡面上的汇流，一般不适合视作连续介质运动。流域剖分除是为了考虑降雨和下垫面空间分布对流域产汇流的影响，还为了分析这种非连续介质运动，是一种物理上的考虑，而非微分方程数值求解的要求。

2 流域产流计算

由于网格尺度可以根据需要任意调整，结果可以使每个网格的下垫面条件基本均匀，网格中的降雨空间分布也基本均匀，因此，蓄满产流模式和超渗产流模式的网格产流量可分别按下列公式计算[7]:

R=P-E-D

(1)

和rs=i-e-fp

(2)

式中：R为网格的蓄满产流量；rs为网格的超渗地面产流率；P、i分别为网格的降雨量和降雨强度；E、e分别为网格的雨期蒸散量和蒸散发率；D为网格包气带缺水量；fp为网格的地面下渗能力。

令P′=P-E,i′=i-e,式(1)(2)又可分别写为

R=P′-D

(3)

和rs=i′-fp

(4)

由式(1)和式(2)可知，如果网格产流属于蓄满产流模式，则计算网格产流量需已知网格的降雨量、雨期蒸散发量和包气带缺水量；而如果网格产流属于超渗产流模式，则计算网格产流量需已知网格的降雨强度、雨期蒸散发率和地面下渗容量。由于网格的数量庞大，故网格产流量的计算必须由“大数据”来支撑。

网格产流计算的结果就可得到如图2(图中网格圆圈内的数字为网格产流量，无数字网格表示该网格无产流量产生)所示的降雨时段或降雨时刻产流网格的空间分布，这就是降雨和下垫面空间变异性共同导致的产流量的空间分布。据此可以求得流域产流量，且可以用实测流域产流量评价其计算精度。

图2 流域网格产流量的空间分布

3 “网格水滴”的汇流时间

若将流域上那些降雨后有产流量的网格视作水滴，称之为“网格水滴”(图3)，则“网格水滴”要在重力驱动和阻力影响下沿地面坡度方向运动，最终的归宿是流域出口断面。每个“网格水滴”将在何时到达流域出口断面取决于其路径的长度和其在路径轨迹上的运动速度。图3中，已知第i个“网格水滴”汇集到流域出口的路径，其长度为ri，假设水滴运动速度随路径而变，记为vi(x)，则易知该“网格水滴”汇集至流域出口断面的汇流时间为

(5)

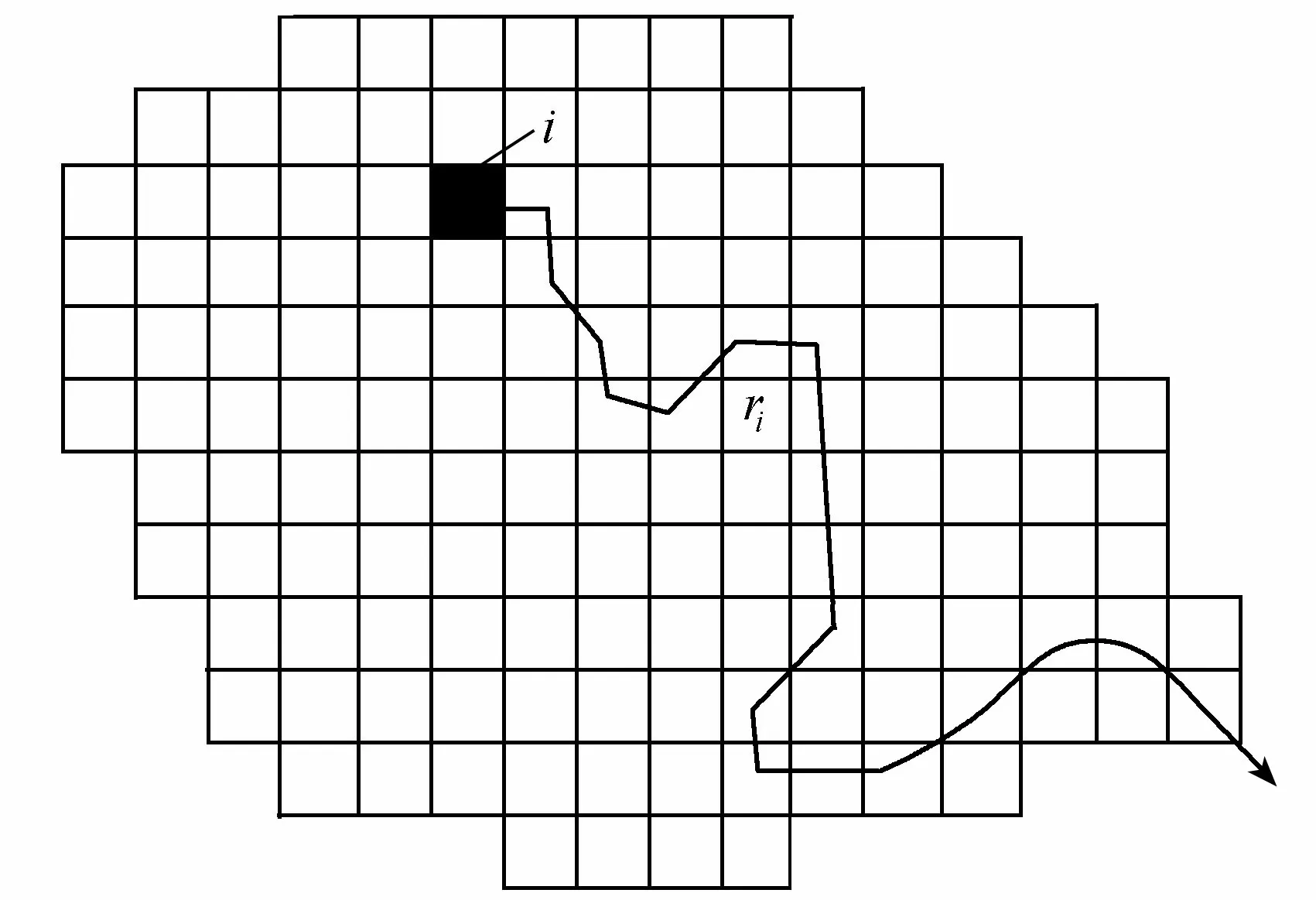
图3 第i个“网格水滴”路径

“网格水滴”的路径及其长度由DEM提取，若“网格水滴”在河道中，则按Manning公式确定其运动速度；若在坡面上，建议用下式确定运动速度[7]:

vs=as1/2

(6)

式中：vs为“网格水滴”在坡面上的运动速度；s为坡面坡度，由DEM提取；a为经验系数，主要与坡面粗糙程度有关。

欲由DEM提取“网格水滴”的路径及其长度，必须先确定水滴从一个网格向相邻网格运动的方向，这已是一项成熟的技术[8]，但用式(6)确定水滴在网格中的运动速度尚未得到实验结果的佐证，一般只能通过率定求得。

4 流域基本单元出流量的形成

图4由图2与可以求得每个“网格水滴”汇流时间的图3叠加而成，是同时表示“网格水滴”汇流时间和网格产流量的空间分布。每个网格中有2个数字：圆圈外的数字表示“网格水滴”汇流时间，由式(5)确定；圆圈内的数字表示网格产流量，由式(3)或式(4)确定。产流量大于零的网格集合起来就是产流区，产流量为零的网格集合起来就是不产流区。唯有产流区才有净雨滴向流域出口断面汇集，参与出口断面流量的形成。每场降雨的时空分布不同，不同时间的包气带缺水量或地面下渗能力的空间变异性也不相同。因此，产流区是随时变动的，汇流的结果也必然随时变动。

图4 网格水滴及汇流时间矩阵

如果第0时刻的降雨形成了如图4所示的网格产流量的空间分布(见图4中圆圈内数字)，则根据图4圆圈外数字即网格的汇流时间可得第1时刻到达出口断面的净雨量为9个单位；同理，可求得第2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17时刻到达出口断面的净雨量分别为12、42、45、17、16、19、9、11、14、32、37、35、32、20、13、9个单位。据此结果就可求出第0时刻降雨形成的流域出口断面流量过程。如果降雨是一个时间过程，则对每时刻降雨用上述同样的方法可求得各时刻降雨形成的流域出口断面流量过程。将不同时刻降雨形成的流域出口断面流量过程同时刻相加，就得到一定时空分布降雨落至流域基本单元形成的出口断面流量过程。

上述对流域基本单元出口断面流量形成和计算方法的认识是否合理，主要取决于两个“相加”是否合理。关于不同时刻降雨形成的流域出口断面流量同时刻相加的合理性已在文献[7]中论述。关于不同“网格水滴”在形成流域出口断面流量过程时也采用同时刻相加是否合理的问题，笔者试图借用Lepold和Langbein关于自然界天然水系形成机理来加以解释。

“随机游移”是概率论中模拟“最可能状态”的一种常用方法。20世纪60年代初，Lepold[9]和Langbein[10]曾利用该方法探讨自然界天然水系的形成机理。由于地面坡度对水系的形成起着重要作用，因此，一般分两种情况来探讨这个问题。当地面坡度较陡时，雨滴落至地面易形成细沟沿坡度方向运动(图5(a))，这些细沟初始流向由地面坡度决定。由于水滴运动方向的随机变化，一旦它偏离原来的运动方向，就可能导致合并。两条细沟相遇就合并成一条较大一点的细沟，如此随机地发展下去就形成了几乎为平行状的扇形二分叉水系。为了讨论地面坡度较缓时水系形成的机理，将地面网格化(图5(b))，由于每个网格的下垫面情况基本一致，因此，每个“网格水滴”向上、下、左、右4个方向运动的概率可认为是相等的，各为0.25。这时，根据随机试验方法即Monte-Carlo方法生成的水系将为树枝状二分叉水系。Lepold和Langbein利用“随机游移”方法生成的水系之所以具有合理性，是因为它们符合Horton地貌定律。笔者认为，Lepold和Langbein对自然界天然水系形成机理的合理解释，是基于同时刻到达流域出口断面的“网格水滴”可以相加，而不必考虑它们之间的相互干扰。

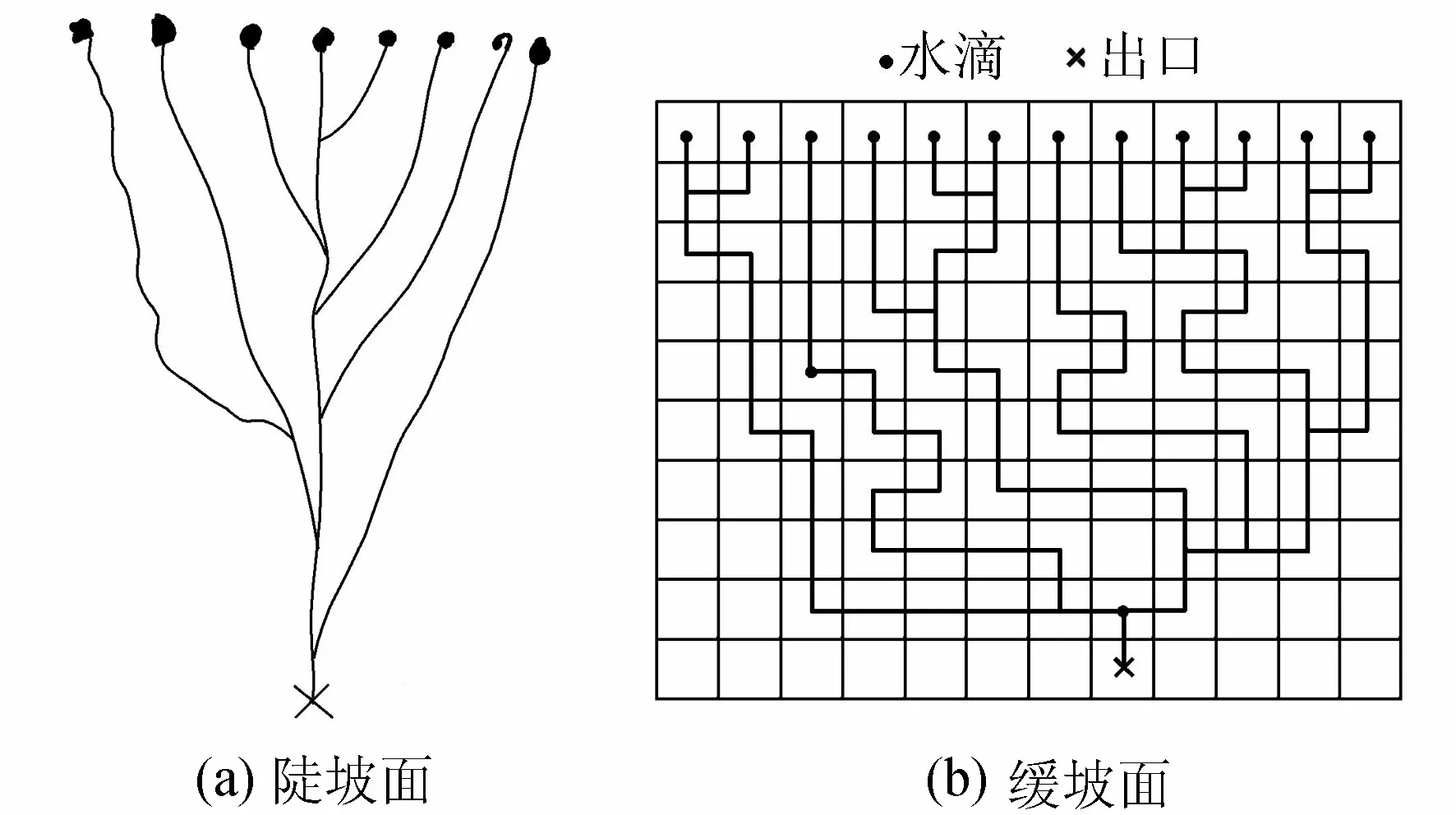
图5 水系形成示意图

5 流域汇流计算

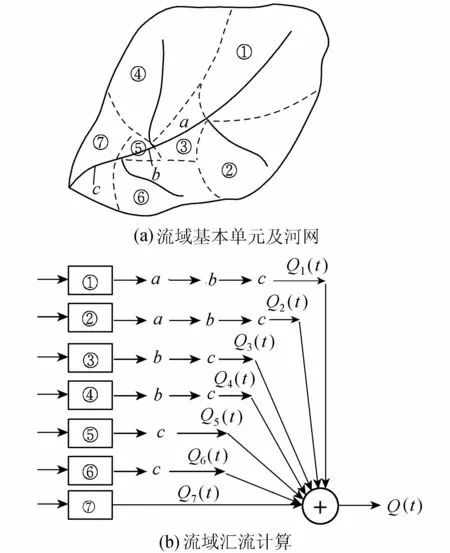
图6 单元嵌套网格结构的流域汇流

由于应用单元嵌套网格剖分法可将一个流域概化为若干网格化流域基本单元，并经由水系连接而成串并联结构，因此，在求得其中每个流域基本单元出口流量过程后，再通过河网汇流就可得到流域出口断面流量过程。这就是说，流域汇流是流域基本单元汇流与河网汇流的结果(图6)。这种处理流域汇流的思想，由于较Sherman单位线法物理概念清晰，早在20世纪60年代就被水文学者发现并使用,这种思想被中国水文学家称为“成因汇流理论”[11]。英国水文学家Price在1978年发表的文章中称这种思想为“河流-流域模型”[12]。这样处理流域汇流的实质是认为流域基本单元汇流和河网汇流的理论基础有别，后者可用连续介质力学处理，前者应使用非连续介质方法处理。

本文使用的单元流域为“流域基本单元”，分析单元流域汇流的基础是“网格水滴”。因此，本文方法较前人提出的方法具有更清晰的物理概念，可以在“大数据”的支持下，对流域汇流现象作精细刻画，充分考虑降雨空间分布和下垫面空间变异性对流域产汇流的影响。

6 与R-V地貌瞬时单位线比较

Rodriguez-Iturbe和Valdes[13]基于统计物理思想和流域水量平衡原理，于1979年证明了流域瞬时单位线u(t)的本质是均匀分布在流域上的无穷多个净雨水滴随机运动到流域出口所用时间即流域汇流时间的概率密度fB(t):

u(t)=fB(t)

(7)

式(7)的发现，揭开了寻求流域瞬时单位线的新途径。水文学历史上第一个按式(7)所揭示的途径确定流域瞬时单位线的方法也是由Rodriguez-Iturbe和Valdes提出来的。他们基于流域汇流的物理过程，提出状态、状态路径、状态转移、状态转移概率、状态等待时间概率等概念，利用概率论理论导出了下列流域瞬时单位线表达式：

(8)

其中p(s)=πx1px1x2px2x3…pxk-1xk(k=2，3，…)

式中：xk为状态，有河流状态和坡面状态之分；πx1为净雨滴落地时所处状态之概率，称为初始概率；pxk-1xk为净雨滴从状态xk-1转移到状态xk的概率，称为状态转移概率；s为净雨滴向流域出口断面运动所取的路径，由其所经由的状态串联而成；S为路径之集合，S={s1，s2,…};p(s)为净雨滴取路径S向流域出口断面运动的概率；fxk(t)为净雨滴在状态xk等待通过所需时间的概率密度，称为状态等待时间概率密度；“*”为表示卷积分的运算符号。

由于根据式(8)和式(9)确定流域瞬时单位线是由Rodriguez-Iturbe和Valdes提出来的，故称之为R-V地貌瞬时单位线。

本文提出的方法是建立在“网格水滴”概念基础上的。由于雨滴之降落是一个随机事件，因此，“网格水滴”汇流时间是随机变量。这样，图4中每个网格圆圈外的数字所表达的矩阵就是从其总体中随机抽取的一个“网格水滴”汇流时间样本，对此进行数理统计分析就可求出“网格水滴”汇流时间的概率密度，即流域瞬时单位线，笔者称此为“网格水滴”地貌瞬时单位线。

将“网格水滴”地貌瞬时单位线与R-V地貌瞬时单位线进行比较，可得如下几点认识:

a. R-V地貌瞬时单位线将某时刻空间分布均匀降雨视作无穷个雨滴均匀分布在流域上，而“网格水滴”地貌瞬时单位线则将某时刻空间分布均匀降雨视作有限个“网格水滴”均匀分布在流域上。因此，R-V地貌瞬时单位线中的水滴是抽象的、无形的，而“网格水滴”地貌瞬时单位线中的水滴是具体的、有形的，其大小及数量由网格尺度决定。

b. R-V地貌瞬时单位线的状态路径作为水滴的汇流路径，其数目取决于流域的Strahler级[14],而“网格水滴”地貌瞬时单位线采用“网格水滴”运动的几何轨迹作为其汇流路线，一个“网格水滴”对应着一条汇流路径。因此，R-V地貌瞬时单位线中的水滴汇流路径是抽象的，只见状态串联，不见几何长度，水滴数无穷，但汇流路径却有限，而“网格水滴”地貌瞬时单位线中的“网格水滴”汇流路径是具体的，每个“网格水滴”的汇流路径既有自己的轨迹，也有一定的几何长度。

c. R-V地貌瞬时单位线中的水滴向出口断面运动只是状态的转移，没有时间的概念，必须引入状态等待时间概率密度才能体现出汇流时间，而“网格水滴”地貌瞬时单位线中的“网格水滴”向出口断面运动不仅有运动轨迹，而且有几何长度和运动速度，可以直接确定每个“网格水滴”的汇流时间。因此，R-V地貌瞬时单位线中汇流时间的体现比较抽象，而且状态等待时间概率密度至今无法从理论推导得出，而在“网格水滴”地貌瞬时单位线中，每个“网格水滴” 的汇流时间具体而明确，物理概念清晰。

d. 若采用负指数函数作为状态等待时间概率密度，则可以证明R-V地貌瞬时单位线的公式结构与线性水库串并联导出的瞬时单位线表达式基本一致，而“网格水滴”地貌瞬时单位线则可做到一个流域一个样[15]，因此，以负指数函数作为状态等待时间概率密度的R-V地貌瞬时单位线所能达到的精度大体上与线性水库串并联导出的瞬时单位线相当，优势不甚明显，而“网格水滴”地貌瞬时单位线则可以根据每个流域的特点“量体裁衣”，理论上也许可以期望获得较高的计算精度。

Rodrignez-Iturbe和Valdes所创立的理论，虽然未能触及单位线的局限性问题，没有解决净雨空间分布不均时使用单位线不合理的问题，但所揭示的规律，以及所导出的R-V地貌瞬时单位线表达式对汇流理论具有非常重要的贡献，他们在水文学中开启的新科学思维方式，是在设法改进传统的流域汇流计算方法如等流时线法、单位线法等几乎陷入困境、流域汇流研究处于低潮的情况下出现的“一盏指路明灯”，它所掀起的地貌单位线研究热潮延续至今[16-17]。笔者提出的“网格水滴”地貌瞬时单位仅是对R-V地貌瞬时单位线的一点补充。

7 等流时线和单位线的重新解读

按照等流时线概念，位于其上的水滴将经历相同的汇流时间到达流域出口断面，而且不同汇流时间的等流时线不可能相交。但由图4可以发现，这样的等流时线一般是不存在的。事实上，只有当每个水滴的运动速度相同时才存在，而这种情况一般只能出现在下垫面完全均一的条件下，例如飞机场跑道、高等级公路等。在一般情况下，等流时线实际上只是一条“等距离线”，只能反映水滴到流域出口断面的运动距离，而不能反映水滴真实的汇流时间。因此，建立在等流时线概念上的等流时线法是一个物理概念并不严谨，无法反映水滴汇流速度分布不均的流域汇流计算方法。

现有的水文学文献一再证明，流域瞬时单位线的本质是水滴汇流时间的概率密度。这显然也是流域单位线的本质所在，这与要求净雨水滴空间分布均匀是一致的。因此，无论是根据实测降雨、径流资料识别流域单位线，还是利用流域单位线进行流域汇流计算都必须以净雨空间分布均匀为前提。遗憾的是，这一重要物理概念长期以来常常被忽视，以致在单位线的研究和应用中出现了一些混乱。

等流时线法和单位线法，作为传统的流域汇流计算方法都创立于20世纪30年代，对水文学的发展均作过重要贡献。但由于对它们的物理基础深入揭示不够，在实践中出现的一些令人纠结的问题，难以得到圆满解决。例如针对等流时线法计算结果洪峰偏大、峰形偏尖瘦、退水段偏快的问题，Clark[18]提出将等流时线法与线性水库串联，以对等流时线法进行改进；针对不同次洪水分析出的单位线往往有较大差别的问题，中国水文工程师提出按暴雨中心位置分别率定单位线[4]，以对单位线法进行改进。这些改进由于均未触及物理概念上存在的缺陷，因此，仅为实际应用中的权宜之计。

分析本文提出的网格水滴汇流理论不难发现，它既不需要去虚构一组等流时线，也不需要去挑选净雨空间分布均匀的降雨径流资料去率定单位线，就能从净雨注入点距出口断面远近和净雨滴运动速度的空间分布两方面考虑所引起的流域调蓄作用，就能将降雨和下垫面变异性对流域汇流的影响考虑得一清二楚，它既保持了等流域法和单位线法的优点，又克服了两者的缺点。因此，用“网格水滴”流域汇流计算方法去统一等流时线法和单位线法已具有可能性。

8 结 语

单元嵌套网格剖分法是在对现有各种流域剖分方法进行比较，取长补短的基础上提出来的，能较好地适应使用“大数据”揭示流域产汇流机理、建立流域产汇流计算方法的需要。

单元嵌套网格产汇流理论与连续介质产汇流理论不同，不是试图通过建立并求解微分方程，而是试图借助“大数据”精细刻画降雨和下垫面的空间变异性，进而考虑降雨和下垫面空间变异性对流域产汇流的影响，构建流域产汇流计算方法。

定义并引入“网格水滴”是建立单位嵌套网格产汇流理念的关键。据此，不仅更直观地明确了流域瞬时单位线的物理本质，以及对R-V地貌瞬时单位线理论进行了有益补充，而且提供了进一步解读等流时线和单位线的条件。等流时线，在一般情况下是虚拟的，实质上它是“等距离线”，不能考虑水滴运动速度不同对出口断面流量形成的影响。单位线的前提是净雨空间分布均匀，无论是根据实测降雨径流资料识别单位线，还是利用单位线进行流域汇流计算都必须满足净雨空间分布均匀的条件。

采用单元嵌套网格产汇流理论处理流域汇流的思路，不仅能吸取等流时线法和单位线法的优点，克服两者之缺点，而且又采用了将坡面汇流和河网汇流先分开、后卷积的考察流域汇流的方法，因此是一种物理概念清晰的流域汇流计算方法，提供了从物理上统一等流时法和单位线法的可能性。

在单元嵌套网格产汇流理论中，汇流速度空间分布不均导致的流域调蓄作用是依靠网格尺度来体现，网格太大，由于汇流速度均化过大，可能低估了流域调蓄作用；网格太小则可能给计算带来不便。如何合理地选择网格尺度尚需开展进一步的深入研究。

[1] EAGLESON P S. Dynamic hydrology[M].New York:McGraw-Hill Book Company,1970.

[2] ABBOTT M B,BATHURST J C,CUNGE J A,et al.An introduction to the European hydrologic,“SHE”[J].Journal of Hydrology,1986,87:45-77.

[3] 芮孝芳.水文学与“大数据”[J].水利水电科技进展，2016，36(3)：1-4.(RUI Xiaofang.Hydrology and big data[J].Advances in Science and Technology of Water Resources,2016,36(3):1-4.(in Chinese))

[4] 赵人俊.中国湿润地区洪水预报方法[M].北京：水利电力出版社，1978.

[5] 芮孝芳.水文学研究进展[M].南京：河海大学出版社，2007.

[6] 芮孝芳.水文学原理[M].北京：高等教育出版社，2013.

[7] 芮孝芳.随机产汇流理论[J].水利水电科技进展，2016，36(5)：8-12.(RUI Xiaofang.Random theory of runoff yield and flow concentrati[J].Advances in Science and Technology of Water Resources,2016,36(5):8-12.(in Chinese))

[8] RUI Xiaofang,YU Mei,LIU Fanggui.Calculation of watershed flow concentration based on the grid drop concept[J].Water Science and Engineering,2008,1(1):1-9.

[9] LEOPOLD L B.The concept of entropy in landscape evolution[R].Washington D.C.:[s.n],1962.

[10] LANGBEIN W B.Geometry of river channels[J].Jour Hyd Div Proc Amer Soc Civil Engin,1964,90(2):301-312.

[11] 赵人俊.流域汇流的计算方法[J].水利学报，1962，7(5)：1-10.(ZHAO Renjun.Computation method of watershed flow concentration[J].Journal of Hydraulic Engineering,1962,7(5):1-10.(in Chinese))

[12] PRICE R K.A river catchment flood model[R].[S.l.]:The Institution of Civil Engineers,1978.

[13] RODRIGUEZ-ITURBE I,VALDES J B.The Geomorphologic structure of hydrologrcal response[J].Water Resources Research,1979,15(6):1409-1420.

[14] STRAHLER A N.Quantitative analysis of watershed geomorphology[J].EOS Trans,ASME,1957,38(6):912-920.

[15] 芮孝芳.对地貌瞬时单位线理论的若干评论[J].水科学进展，1991，2(3)：194-200.(RUI Xiaofang.Some reviews on theory of geomorphologic instantaneous unit hydrograph[J].Advances in Water Science,1991,2(3):194-200.(in Chinese))

[16] 芮孝芳.地貌瞬时单位线研究进展[J].水科学进展，1999，10(3)：345-350.(RUI Xiaofang.Some advances in geomorphologic instantaneous unit hydrograph[J].Advances in Water Science,1999,10(3):345-350.(in Chinese))

[17] RUI Xiaofang,LIU Ningning,LI Qiaoling,et al. Present and future of hydrology[J].Water Science and Engineering,2013,6(3):241-249.

[18] CLARK C O.Storage and the unit hydrograph[J].Transactions of the American Society of Civil Engineers,1945,110:1419-1446.

Theory of runoff yield and confluence by grid inlaid in watershed basic unit

RUI Xiaofang

(CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China)

A method for dividing watershed by grid inlaid in watershed basic unit is discussed. As big data can precisely describe space distribution of rainfall and spatial variability of underlying surface, a calculation method based on big data, considering effects of space distribution of rainfall and spatial variability of underlying surface on runoff yield and confluence, is proposed. Through an introduction of “grid drop”, the physical nature of watershed instantaneous unit hydrograph is revealed, and the theory of geomorphologic instantaneous unit hydrograph by Rodriguez-Iturbe and Valdes is supplemented. In addition, the limitations of the isochronism line method and the unit hydrograph method are investigated. It can be concluded that the proposed theory of runoff yield and confluence by grid inlaid overcomes the disadvantage and assimilates the advantages of the two methods mentioned above, and provides a possibility of unifying the two methods.

watershed basic unit; grid drop; runoff yield and confluence; big data; geomorphologic instantaneous unit hydrograph of watershed; isochronism line

国家自然科学重点基金(41130369，41430855)

芮孝芳(1939—)，男，教授，主要从事水文水资源研究。E-mail:jiangguo@hotmail.com

10.3880/j.issn.1006-7647.2017.02.001

P333.2

：A

：1006-7647(2017)02-0001-06