基于不同分布曲线的常州市暴雨组合概率

胡尊乐,张 悦,李 丹，汪 姗

(江苏省水文水资源勘测局常州分局,江苏 常州 213022)

基于不同分布曲线的常州市暴雨组合概率

胡尊乐,张 悦,李 丹，汪 姗

(江苏省水文水资源勘测局常州分局,江苏 常州 213022)

基于常州雨量站1951—2015年的年最大1 d、3 d降水量资料,利用Copula联结函数构建联合分布函数,推算相应的同现重现期和组合风险率,并以此为基础,评价常州市2015年“6·26”暴雨可能的重现期和风险率。结果表明:某一设计标准下的年最大1 d、3 d降水遭遇时的同现重现期大于年最大1 d或3 d降水单变量对应的重现期;同一设计频率的暴雨遭遇的风险率较高,且随着重现期增大而减小;“6·26”暴雨的同现重现期为218 a,同现风险率为17.4%,此次暴雨具有特殊性和罕见性,常州市未来的防洪形势将更为严峻。

暴雨组合;联结函数;年最大1 d降水;年最大3 d降水;常州“6·26”暴雨

在我国南方地区,年最大1 d降水往往对河流洪水的起涨和洪峰的形成起着主导作用,年最大3 d降水对洪峰的叠加、峰值以及洪水的消退有着重要的影响。如2015年6月26—28日,常州市区累计降水量达到315.0 mm,其中26日降水量为174.5 mm,27日降水量为120.0 mm,28日降水量为20.5 mm；受持续强降水影响,京杭运河常州段水位于26日7:00上涨,17:15突破警戒值4.30 m,27日4:30达到5.52 m(1991年最高水位),19:15达到最高值6.43 m,期间平均涨落率为0.08 m/h,最大涨率为0.33 m/h;29日12:30出现第二次洪峰(水位6.25 m)。根据历史暴雨资料(1951—2015年)统计分析,2015年常州市“6·26”暴雨过程中,年最大1 d降水量为174.5 m,为历史第3高值;年最大3 d降水量为315.0 mm,更是达历史最高值。显然,这种不同历时的极端暴雨组合,加剧了常州市洪涝灾害的严重程度(超1991年最高水位0.91 m)和持续时间(5.52 m以上的水位持续时间为93 h)。

目前,对于这种不同历时暴雨的组合概率研究,很多学者广泛采用联结函数(Copula)进行模拟分析,如许月萍等[1]应用几种联结函数模拟了浙江省云港流域不同历时降水量的二元联合分布,曾明等[2]开展了上海市不同历时暴雨组合频率研究。这些研究表明,联结函数在多变量水文参数频率分析中可以有效地解决水文参数之间的非独立性问题,减少单变量水文频率分析的不确定性,这也是联结函数在水文领域的重要应用。但是,这些研究中频率计算倾向采用皮尔逊Ⅲ型(P-Ⅲ型)分布曲线适线成果,缺乏可比性。本文基于不同分布曲线(Gumbel分布和P-Ⅲ型分布),对常州市年最大1 d、3 d降水量进行频率分析,并以2015年常州市“6·26”暴雨为分析对象,探讨本次降水量过程的变化规律和年最大1 d、3 d降水量的概率组合,以及相应的风险性。

1 资料来源与分析

1.1 资料来源

常州雨量站位于常州市主城区,设立于1922年,是太湖流域设立较早的雨量站点之一,资料系列长,观测精度高,也是常州市水利工程设计、城市防洪排涝的代表雨量站。本文研究采用常州雨量站1950年1月至2015年8月近65年的年最大1 d、3 d降水量资料(以下以D1、D3表示)。

1.2 资料分析

对常州雨量站D1、D3两个资料系列分别进行趋势性、变异性和相关性分析(包括自相关性和互相关性),其中,采用线性倾向估计法和Mann-Kendall趋势检验进行趋势性分析[3-4],判断资料系列是否存在显著的趋势变化;采用有序聚类法和滑动秩和检验进行变异性分析[5],判断资料系列是否存在显著的变异;采用自相关系数检验和秩号自相关系数检验进行自相关性分析[6-8],判断资料系列内部是否相互独立;采用线性相关系数检验、Kendall秩相关系数检验和Spearman秩相关系数检验进行互相关性分析[9],判断D1和D3是否相互独立,分析两者相关性。

统一取显著性水平α=0.05进行各种统计检验,常州雨量站D1、D3系列趋势性、变异性和自相关性检验结果见表1～3和图1,互相关性检验的线性相关系数ρ=0.799、Kendall秩相关系数τ=0.538、Spearman秩相关系数ρs=0.729。

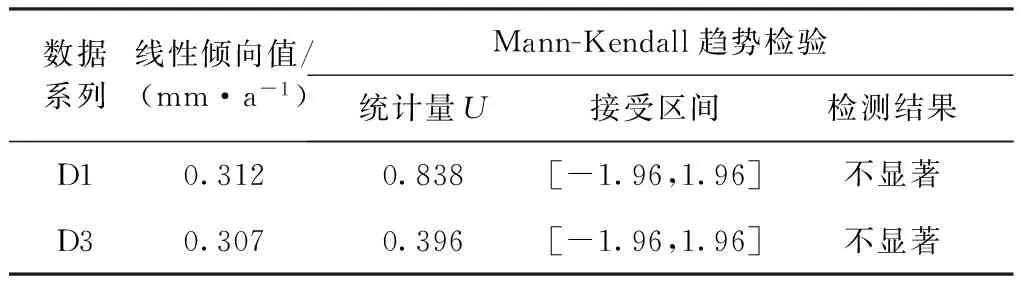
表1 常州雨量站D1、D3系列趋势性检验结果

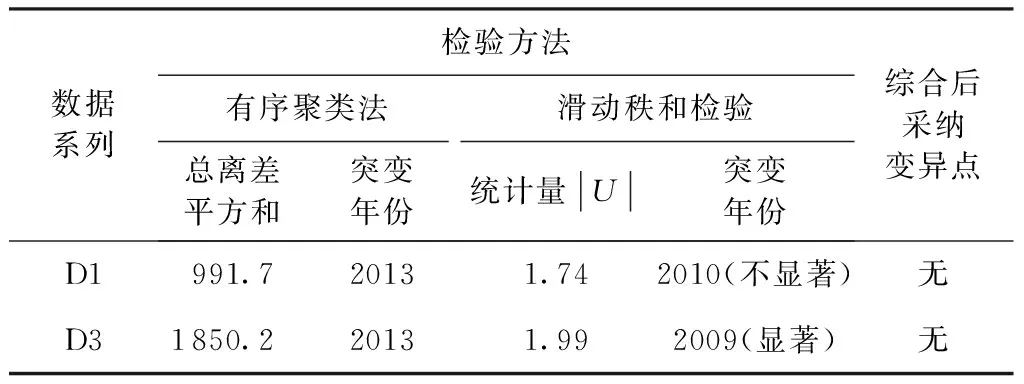
表2 常州雨量站D1、D3系列变异性检验结果

表3 常州雨量站D1、D3系列自相关性检验结果

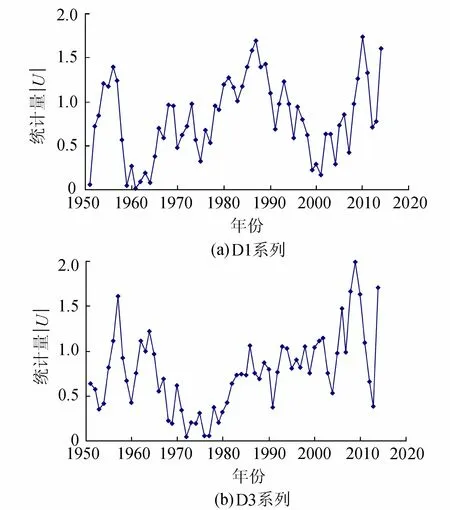
图1 常州雨量站D1、D3系列滑动秩和检验统计量过程

从表1可知,常州雨量站D1、D3系列分别存在0.312 mm/a、0.307 mm/a的平均线性倾向率,而Mann-Kendall趋势检验结果为两个系列趋势变化均不显著。

从图1和表2可以看出,虽然两种方法均检出理论上的可能变异点,但因其靠近系列的开端,统计误差较大,因此检测结果不可靠,综合判定两系列均不存在显著变异点。

从表3可以看出,常州雨量站D1、D3系列内部均不存在相关性,但互相关性检验结果表明两者之间存在一定的相关关系,其线性相关系数ρ、Kendall秩相关系数τ、Spearman秩相关系数ρs分别达到0.799、0.538和0.729。

2 概率计算与分析

2.1 边缘分布函数推求

选择Gumbel分布曲线和P-Ⅲ型分布曲线分别对常州雨量站D1、D3系列进行频率分析。采用计算机编程(VC语言)处理数据,通过输入两个资料系列由程序自动对数据进行由大到小的排序、估计初值、优化参数和适线。其中,以矩法所得参数为适线初值,采用最小二乘法进行参数优化,最终得到较优的适线成果如表4所示,其频率曲线见图2。

表4 常州雨量站D1、D3系列频率计算结果

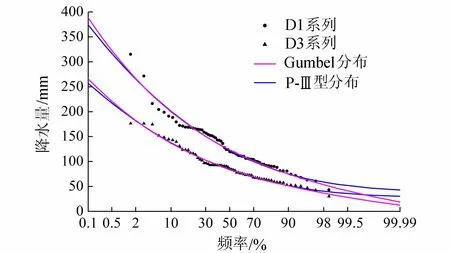
图2 常州雨量站D1、D3系列频率曲线

结合表4和图2可以看出,相对P-Ⅲ型分布曲线,Gumbel分布曲线的设计成果在小概率部分(50年一遇乃至更大暴雨)整体偏大一些,有利于工程设计的安全;同时对于大概率部分(95%～99.99%),Gumbel分布曲线的拟合效果也更理想;而在中间概率部分(5%～90%),二者成果较为接近。因此,采用Gumbel分布曲线的设计成果是合理可信的,具有一定的适应性和优势。

2.2 联合分布函数推求

由前面的分析可知,常州雨量站D1、D3系列之间存在一定的相关性。本文选用水文领域最常用的Archimedean Copula函数族中的Gumbel-Hougaard(G-H)Copula函数[10-13]构建D1、D3系列的联合分布函数:

F(x,y)=exp-[(-lnFX(x))θ+

式中:X和Y为降水事件中的两个特征变量,分别对应于年最大1 d降水量和年最大3 d降水量;FX(x)和FY(y)分别为两特征变量的边缘分布函数。

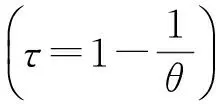
式中:GX(x)、GY(y)分别为年最大1 d降水量和年最大3 d降水量的Gumbel分布函数;PX(x)、PY(y)分别为年最大1 d降水量和年最大3 d降水量的P-Ⅲ型分布函数。

2.3 拟合优度评价

为分析所选Copula函数是否能够有效地描述变量间的相关性结构,需要对Copula函数进行拟合检验。本文将各个观测点据的经验分布频率和理论分布频率进行比较,以检验两变量理论联合分布函数在暴雨组合频率分析中的拟合程度,同时采用Kolmogorov-Smirnov(K-S)检验分布的一致性[15],结果见图3和表5。

图3 经验频率和理论频率比较

表5 理论联合分布K-S检验结果

从图3和表5可以看出,基于不同分布曲线,利用G-H Copula函数构建的常州雨量站年最大1 d、3 d降水量组合的联合分布函数均较为理想。

拟合优度评价是选择联合分布函数的重要指标。本文采用AIC信息准则法和离差平方和最小准则法(OLS)[16-17]进行拟合优度评价,结果见表6。从表6可以看出,在两者对应的OLS值相当的情况下,基于Gumbel分布的G-H Copula函数对应的AIC值更小,拟合效果更好,同时考虑到前述边缘分布函数推求中Gumbel分布曲线的拟合效果也较为理想的情况,本文最终采用基于Gumbel分布的G-H Copula函数做进一步分析。

表6 G-H Copula函数拟合优度评价结果

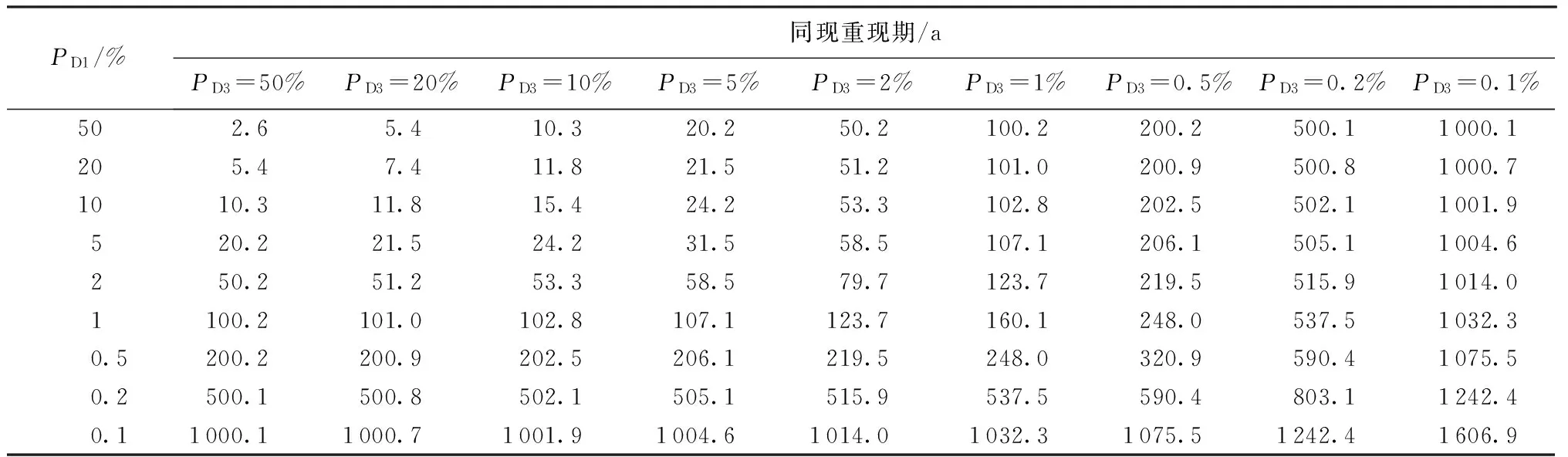
表7 常州雨量站D1、D3系列不同频率设计暴雨的同现重现期计算结果

2.4 同现重现期和同现风险率计算

2.4.1 同现重现期计算

两变量同现重现期为水文事件X、Y都超过某一特定值时发生频率的倒数,用于表征可能出现一次该情况的平均间隔时间,其计算公式为

Ta(x,y)=1P(X>x,Y>y)=

11-FX(x)-FY(y)+F(x,y)

(4)

按式(4)计算得常州雨量站D1、D3系列不同频率设计暴雨的同现重现期如图4(图中WD1、WD3分别为常州雨量站D1、D3系列的设计暴雨)和表7所示。

图4 常州雨量站D1、D3系列不同频率设计暴雨的同现重现期等值线(单位:a)

由表7可以看出,单变量D1、D3的重现期均为2 a时,两者遭遇的同现重现期为2.6 a;当D1、D3的重现期分别为100 a时,两者遭遇的同现重现期约为160 a;当D1、D3的重现期分别为1 000 a时,两者遭遇的同现重现期约为1 607 a。显然,某一频率下D1、D3同现重现期大于单变量(D1或D3)的重现期。这表明,当同时遭遇某一设计频率下的年最大1 d、3 d降水时,常州市所遭遇的洪水往往大于年最大1 d或年最大3 d降水单变量的设计洪水标准,对防洪威胁最大。若采用联合分布的设计标准,更有利于提升常州市的防洪能力。

2.4.2 同现风险率计算

同现风险率是指在一定时空条件下发生多变量非期望事件的概率[18]。考虑到常州地处太湖平原区,境内河网密布、水系纵横的自然地理条件以及主峰在前的暴雨特征,最大1 d降水往往对洪水量级和洪峰的形成起关键作用,同时从充要条件的角度看,发生最大1 d降水是发生年最大3 d降水的必要条件,因此定义常州雨量站D1、D3系列的同现风险率为P(Y>yX>x),即年最大1 d降水大于特定设计值条件下的年最大3 d降水超过设计值的风险率。常州雨量站D1、D3系列不同设计暴雨组合的同现风险率计算结果见表8。

从表8可以看出,D1、D3系列同频率设计暴雨遭遇的风险率很高,如重现期均为2 a的年最大1 d、3 d降水遭遇的同现风险率达到77%,且随着重现期增大而减小。对于某一频率的年最大3 d降水设计值,年最大1 d降水的重现期越大,两者的同现风险率越高;对于某一频率的年最大1 d降水设计值,年最大3 d降水的重现期越大,两者的同现风险率越小。这表明,在发生某一设计频率的年最大3 d降水时,同时遭遇年最大1 d降水的可能性随年最大1 d降水对应的重现期增大而变大;在发生某一设计频率的年最大1 d降水时,同时遭遇年最大3 d降水的可能性随年最大3 d降水对应的重现期增大而变小。

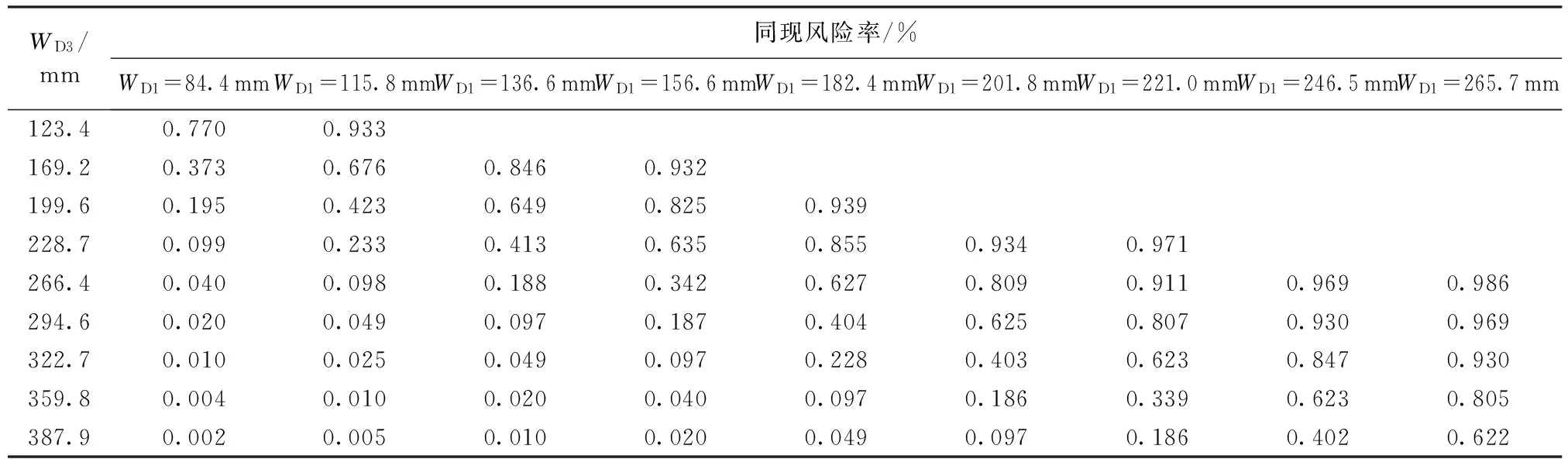
表8 常州雨量站不同设计暴雨组合的同现风险率计算结果

2.5 “6·26”暴雨分析

根据前述边缘分布函数推求的频率分析成果,2015年常州市“6·26”暴雨中,年最大1 d、3 d降水的重现期分别为38 a、192 a,而两者组合时的同现重现期则高达218 a,高于传统单变量的设计标准。此外,两者组合时的同现风险率达到17.4%,说明就理论上而言,当发生38 a一遇的最大1 d降水后,再发生高达192 a一遇的最大3 d降水的可能性本应不大。

根据历年水文资料统计,1951—2015年间,当发生年最大1 d降水后,再发生年最大3 d降水的情况共有38次,占比达58.5%,表明当发生较大的1 d降水后,再发生较大3 d降水的可能性非常高,对常州市防洪排涝威胁较大。然而,在同时遭遇年最大1 d、3 d降水的情形中,统计年最大1 d降水量在年最大3 d降水量中的占比情况,其占比小于或等于2015年的情况只出现9次，其在同时遭遇年最大1 d、3 d降水的情形中,所占比重仅为23.7%,在1951—2015年期间所占比重更是只有13.8%,因此从另一角度表明“6·26”暴雨的特殊性和罕见性,同时也表明随着气候变化和人类活动的影响,下垫面产汇流条件改变,极端降水事件发生的概率增大,常州市未来的防洪形势将更为严峻。

3 结 论

a. 常州市年最大1 d、3 d降水量系列均不存在显著的趋势变化,但呈现弱上升趋势,且均未发生显著性变异,两者之间存在一定的相关性。

b. 相对P-Ⅲ型分布曲线,Gumbel分布曲线对常州市年最大1 d、3 d降水量系列进行频率分析的拟合效果更优,其设计成果在小概率部分偏大一些,有利于工程设计的安全。水文上不常使用的Gumbel分布曲线更适合于常州市年最大1 d、3 d降水量系列的频率分析。

c. 常州市“6·26”暴雨的同现重现期达到218 a,同现风险率仅为17.4%,表明此次暴雨具有特殊性和罕见性,常州市未来的防洪形势将更为严峻。

[1] 许月萍,童杨斌,富强,等.几种Copulas模拟不同历时降雨量的影响分析[J].浙江大学学报(工学版),2009,43(6): 1107-1111.(XU Yueping,TONG Yangbin,FU Qiang,et al.Impact analysis for rainfall depthsimulation of different durations through several Copulas[J].Journal of Zhejiang University(Engineering Science),2009,43(6):1107-1111.(in Chinese))

[2] 曾明,张雨凤,李琼芳,等.上海市不同历时暴雨组合概率研究[J].水资源保护,2015,31(4):82-86.(ZENG Ming,ZHANG Yufeng,LI Qiongfang,et al.Study on probability for rainstorm combinations during different durations in Shanghai City[J].Water Resources Protection,2015,31(4):82-86. (in Chinese))

[3] 魏凤英.现代气候统计诊断与预测技术[M].北京:气象出版社,2007.

[4] 王金花,康玲玲,赵广福.基于Mann-Kendall法的水沙系列突变点研究[J].人民黄河,2010,32(1):42-45.(WANG Jinhua,KANG Lingling,ZHAO Guangfu.Analysis of change point detection of water and sediment series based on Mann-Kendall method[J].Yellow River,2010,32(1):42-45. (in Chinese))

[5] POTTER K W.Illustration of a new test for detecting a shift in mean in precipitation series[J].Monthly Weather Review,1981,109:2040-2045.

[6] REEVES J,CHEN J,WANG X L,et al.A review and comparison of change point detection techniques for climate data[J].Journal of Applied Meteorology and Climatology,2007,46:900-915.

[7] 符淙斌,王强.气候突变的定义和检测方法[J].大气科学,1992,16(4):482-493.(FU Congbin,WANG Qiang.The definition and detection of climate abrupt change[J].Scientia Atmospherica,1992,16(4):482-493. (in Chinese))[8] 谢平,陈广才,雷红富.变化环境下基于趋势分析的水资源评价方法[J].水力发电学报,2009,28(2):14-19.(XIE Ping,CHEN Guangcai,LEI Hongfu.The assessment method of water resources based on trend analysis of changing environments[J].Journal of Hydroelectric Engineering,2009,28(2):14-19. (in Chinese))

[9] 李国芳.感潮河段水文计算方法研究[D].南京:河海大学,2003.

[10] GUMBEL E J.Multivariate exeme distributions[J].Bulletin of the International Statistical Institute,1960,39(2):471-475.

[11] 熊立华,郭生练.两变量极值分布在洪水频率分析中的应用研究[J].长江科学院院报,2004,21(2):35-37.(XIONG Lihua,GUO Shenglian.Application study of a bivariate extremal distribution in flood frequency analysis[J].Journal of Yangtze River Scientific Research Institute,2004,21(2):35-37. (in Chinese))

[12] 林荣,李国芳.黄浦江风暴潮位、区间降雨量和上游来水量遭遇分析[J].水文,2000,20(3):1-5.(LIN Rong,LI Guofang.Analysis of the upstream floods meeting with storm tide and interval rainfall in the Huangpu River[J].Journal of China Hydrology,2000,20(3):1-5. (in Chinese))

[13] 谢华,黄介生.两变量水文频率分布模型[J].水科学进展,2008,19(3):443-452.(XIE Hua,HUANG Jiesheng.A review of bivariate hydrological frequency distribution[J].Journal of Advances in Water Science,2008,19(3):443-452. (in Chinese))

[14] 杜江,陈希镇,于波.Archimedean Copula函数的参数估计[J].科学技术与工程,2009(3):637-640.(DU Jiang,CHEN Xizhen,YU Bo.Parameter estimation of Archimedean Copula[J].Science Technology and Engineering,2009(3):637-640. (in Chinese))

[15] 南波.基于K-S检验法的雪荷载统计分析[J].兰州理工大学学报,2002,38(1):115-119.(NAN Bo.Statistical analysis of snow load based on K-S inspection method[J].Jounal of Lanzhou University of Technology,2002,38(1):115-119. (in Chinese))

[16] 单国莉,陈东峰.一种确定最优Copula的方法及应用[J].山东大学学报(理学版),2005(4):66-69.(SHAN Guoli,CHEN Dongfeng.A method to determinate the optimal Copulas and its application[J].Journal of Shandong University(Natural Science),2005(4):66-69. (in Chinese))

[17] WANG Cheng,CHANG Nibin, YEH G T.Copula-based flood frequencyanalys is at the confluences o f confluences of river system [J].Hydrological Processes,2009(2):7273-7288.

[18] 傅湘,王丽萍.洪水遭遇组合下防洪区的洪灾风险率估算[J].水电能源科学,1999,17(4):23-26.(FU Xiang,WANG Liping.Estimating flood hazard risk rate of flood control region under flood encountering combination[J].Water Resources and Power,1999,17(4): 23-26. (in Chinese))

Probability of rainstorm combinations in Changzhou City based on different distribution curves

HU Zunle, ZHANG Yue, LI Dan, WANG Shan

(ChangzhouBranchofJiangsuProvinceHydrologyandWaterResourcesInvestigationBureau,Changzhou213022,China)

Based on annual maximum 1-day and 3-day rainfall data from the Changzhou precipitation station from 1951 to 2015, a joint distribution function was constructed using the Copula function, and the corresponding co-occurrence return period and risk of rainstorm combination were calculated. Then, the function was used to evaluate the probable return period and risk of a rainstorm in Changzhou City on June 26, 2015. The results show that the co-occurrence return period when the annual maximum 1-day and 3-day rainfall according to a certain design standard encounter is larger than the respective return periods of annual maximum 1-day and 3-day rainfall. The risk when two rainstorms with the same design frequency encounter is higher, and will decrease with the increase of the corresponding return period. The co-occurrence return period of the rainstorm in Changzhou on June 26 is 218 years, when the co-occurrence risk is only 17.4%, indicating that this rainstorm is special and rare. Flood control in Changzhou City still faces severe issues in the future.

rainstorm combinations; Copula function; annual maximum 1-day rainfall; annual maximum 3-day rainfall; rainstorm in Changzhou on June 26, 2015

胡尊乐(1970—),男,高级工程师,主要从事水文水资源研究。E-mail:1220128265@qq.com

张悦(1990—),女,助理工程师,主要从事水文水资源研究。E-mail:734802746@qq.com

10.3880/j.issn.1006-7647.2017.02.012

P333.2

：A

：1006-7647(2017)02-0068-05

2016-01-31 编辑：熊水斌)