基团贡献法估算有机化合物临界温度的研究进展*

郑文龙，蒋丽红，王亚明，刘 磊

(昆明理工大学 化学工程学院，云南 昆明 650500)

物质的临界参数作为描述物质特性的基础物性数据，是物质热力学性质的重要组成部分，其中临界温度Tc不但是计算流体的许多其它热力学性质的基础，而且一些至关重要的热力学函数计算及应用，如气体状态方程的应用以及石油化工生产控制、化工流程模拟和设计更是离不开这些数据。因此，Tc的准确度在很大程度上决定了物性估算的可靠程度及相关计算和设计的可行性。每年都有成百上千种新的有机化合物问世，因此随之而来的有机物物性研究备受关注。目前通过测定获得临界参数的有机物仅有约600种，其中绝大多数是稳定物质，不稳定物质因测定难度大，其临界数据很少[1-3]，远远不能满足化工生产和设计的需求。

研究者们在致力于提高实验技术的同时，也花费了大量的精力以谋求简便而准确的临界温度的估算方法。现有的估算方法可分为基于液体状态方程的估算法[4-6]、其它物性相关联的半经验估算法[7-8]以及基团贡献法[3,9]3种。基于液体状态方程的估算法因估算需要使用的物性参数多，如饱和液体的pVT和一些其它系数，通用性差；其它物性相关联的半经验估算法采用摩尔质量、密度或沸点为自变量进行估算，其缺乏理论基础，任意性大，整体误差高于基团贡献法；基团贡献法计算过程虽然繁琐，但是不需要过多的物性参数，使用较方便，不仅如此，由于具有完善的官能团参数，应用比较广泛。目前基团贡献法是估算Tc的最具实用价值、最准确、最普遍的方法。

1 估算方法

德国学者Riedel在1952年最先有效地利用基团加和性原理来计算临界温度。1955年，Lydersen提出了第一个基团划分比较细致，估算结果较好的基团贡献方法。1979年，Ambrose法被提出，其计算公式简单。1982年，Fedors论述的方法计算Tc时不需要正常沸点Tb。1984年，Joback在实验数据和基团划分上都对Lydersen法作了补充和改进，其通过回归分析得到关联式。马沛生等人在1990年对Ambrose法进行改进，所得方法计算精度优于Ambrose法，而且使用单位及式中各参数的意义与Joback法相同。1994年，Constantinou和Gani针对其它方法未考虑分子中相邻基团间的相互影响以及不能区分同分异构体等方面的缺陷进行了改进，引入了二级基团，从而提出了新方法。1996年，Wilson和Jasperson提出了能同时计算无机物和有机物的方法。1999年，Marrero-Pardillo提出了键贡献法。最近几年出现了张克武-张宇英法和定位分布基团贡献方法等新方法。

1.1 Riedel法

1952年，德国学者Riedel最先利用基团加和性原理来计算Tc。

(1)

式中，Tc为临界温度，K；Tb为正常沸点，K；Nk为分子中k型基团的数目；tck为k型基团的临界温度的贡献值。

该方法由于基团划分比较简单及精度不高，后续学者未对其进行更进一步研究[10-11]。

1.2 Lydersen法

1955年，Lydersen提出了第一个基团划分比较细致，估算结果较好的基团贡献方法[12]。

(2)

该方法在1987年前被称为精度最高的公式[13-15]。此法为后续的基团贡献法提供了研究思路与基础[16]。其缺点是它不能区分结构类似的异构体。对C1～C20的烷烃和C3～C14的其它烃类化合物的检验，临界温度与实验值的误差一般小于2%，但对相对分子质量较大(例如7 100)的非极性物质误差可高达5%，而且对含多功能极性基团的物质的估算精度不确定[17]。

1.3 Ambrose法

1979年，Ambrose等人提出了改进有机氟或卤代物基团划分的估算临界温度的基团贡献法[18]。

(3)

该法由于没有考虑到微观电子效应的复杂性，因此基团数过多[19]。与Lydersen法和Joback法类似，都不考虑各种基团间的交互作用，计算公式比较简单[20]。但是该方法应用比较困难，主要是不易估算含多官能团的氟化物和醇类的Tc[13,21]。

1.4 Fedors法

1982年，Fedors在分子结构基础上提出了下述估算方法[22]。

(4)

该方法计算Tc时不需要Tb，适用于计算摩尔质量高或极不稳定而难于测定Tb的物质。Reid等的专著[23]中曾用9个化合物对这种方法进行了验算，其平均误差为9.84%，最大误差为45%。

该方法由于不像其它方法需要Tb实验值，当缺少Tb实验值时，该方法不仅可以大大减少工作量，而且估算精度相对较高。

1.5 Joback法

1984年，Joback在实验数据和基团划分上都对Lydersen法作了补充和改进，提出了著名的Joback公式[24-25]。

(5)

(6)

式中，tbk为k型基团的正常沸点的贡献值。

Joback法估算相关物质的Tc和文献实验值的比较结果见表1。

表1 Joback法估算相关物质的Tc和文献实验值的比较结果[16]

1) 文献中可用于检验本方法的物质数量；2) 文献中碳原子超过3个、可用于检验本方法的物质数量；3) AAE表示性质的平均绝对误差；A%E表示平均绝对百分比误差；4) 绝对百分比误差大于10%的物质数量；5) 绝对百分比误差小于5%的物质数量；误差在5%～10%的物质数量能由表中数据确定。

由表1可见，只要使用Tb实验值，无论分子大小如何，此法估算得到的所有物质的Tc都十分可靠；而当使用估算值Tb时，误差明显增大，但对有3个及以上的碳原子数的化合物，误差增大相对较小(表中标有“2)”的物质其平均绝对百分比误差增加2.39%，标有“1)”的整个数据库平均增加3.82%)[16]。

该方法对大分子物质的估算值普遍偏小，而对卤化合物的估算值往往偏大。对于烷烃、烯烃等烃类，此方法比较适用。但是对醇类等物质，该方法计算误差高达4%或5%以上，并且几乎都是负误差。原因可能是Joback在研究—OH时没有考虑到醇的氢键和缔合性[11]。

1.6 MXXC法

1990年，马沛生等人对Ambrose法进行改善，改进了基团的划分提出了该方法。

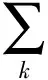
(7)

该方法更好地对芳环、非芳环、萘环上的基团以及芳环上取代基、非芳环上取代基、萘环上取代基进行了细分，同时将含氟或含氯烷烃中碳原子上的氢单独划分出来，提高了估算准确度，其计算精度要高于Ambrose法[17,26]。该方法所用单位及式中各参数的意义与Joback法一致，马沛生等用经过严格筛选的275种化合物进行验算，Tc的平均误差为0.75%[27]。对炔烃、高级烷烃(C14以上)、胺类、醇类、酚类、卤代链烃、芳卤烃等结构类型，该估算式不适用，误差在15%以上的很多[1]。

1.7 C-G法

1994年，Constantinou和Gani提出了一种新的估算临界温度的基团贡献法[28]。

(8)

式中，Nk为分子中k类一级基团的数目；tc1k为1k的一级基团的临界温度的贡献值；Mj为分子中j类二级基团的数目；tc2j为2j的二级基团的临界温度的贡献值；一级计算时W设为0，二级计算时设为1。

该方法是在Lydersen、Joback等方法基础上，针对其未考虑分子中相邻基团间的相互影响和不能区分同分异构体等方面的缺陷进行了改进，加入了二级基团而提出来的。与C-G法相似的方法还有W-J法、M-P法、L-M法等，这些方法都考虑了相邻基团的作用[25]。

C-G法估算相关物质的Tc和文献实验值的比较结果见表2，碳原子超过3个的物质的Tc比较结果见表3。

表2 C-G法估算相关物质的Tc和文献实验值的比较结果[16]

1) 文献中可用于检验本方法的物质数量；2) AAE表示性质的平均绝对误差；A%E表示平均绝对百分比误差；3) 绝对百分比误差大于10%的物质数量；4) 绝对百分比误差小于5%的物质数量；误差在5%和10%之间的物质数量能由表中数据确定；5) 使用二级基团求性质的物质数量；6) 二级结果比一级更精确的物质数量；7) 与一级相比，二级的平均改进程度，负值表示总体上二级精确度更低。

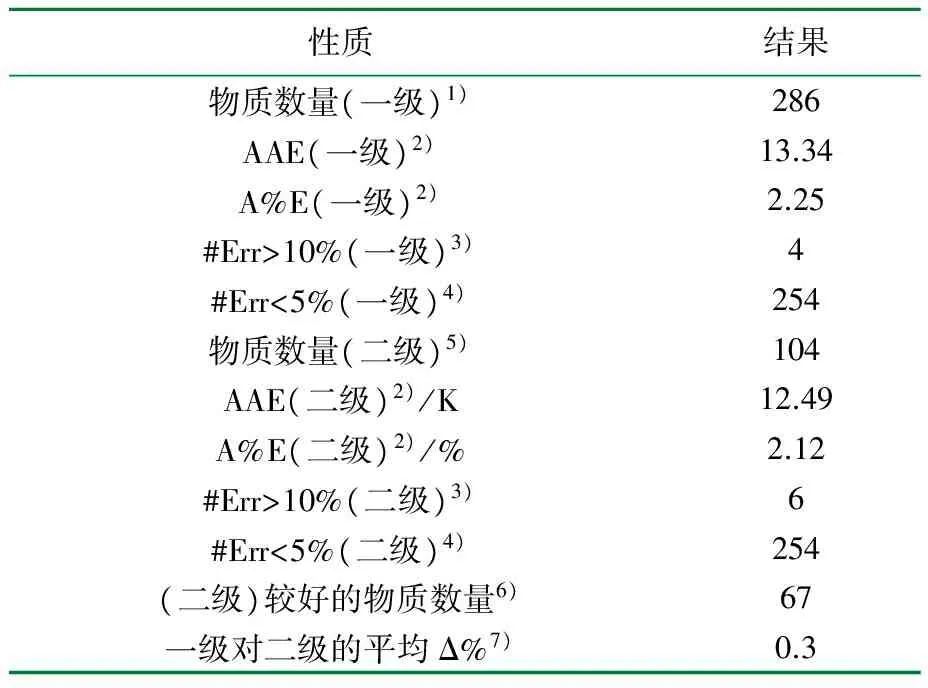
表3 C-G法估算碳原子超过3个的物质的Tc和文献实验值的比较结果[16]

1) 文献中可用于检验本方法的物质数量；2) AAE表示性质的平均绝对误差；A%E表示平均绝对百分比误差；3) 绝对百分比误差大于10%的物质数量；4) 绝对百分比误差小于5%的物质数量；误差在5%和10%之间的物质数量能由表中数据确定；5) 使用二级基团求性质的物质数量；6) 二级结果比一级更精确的物质数量；7) 与一级相比，二级的平均改进程度，负值表示总体上二级精确度更低。

由表2、表3可知，大多数情况下该方法精确度较高，但对小分子物质来说有着明显误差，表2比表3的误差大。这是由于即使小分子物质可能是基团构成的，但是基团相加并不太精确。一般，C-G法对小分子和大分子物质的误差较大，尤其是氟化物和较大分子的环状(结构)化合物。估算结果可能过大或过小，没有显著的误差特征。

在多数情况下，二级贡献的引入对结果的正面和负面影响均为1～3倍，但环状(结构)化合物和石蜡除外，其误差变化很少超过1%～2%。因此二级贡献的改进作用往往非常有限，只有少数物质引入这种额外的复杂计算才有意义。在实际应用中，通过确定基团二级贡献值的大小，可以作为是否采用二级贡献的判断依据[16]。

马沛生用285个化合物进行Tc估算，只用一级基团的平均误差为1.62%，加上二级基团后误差降低到0.85%[27]。

Yan Xinjian等人用该方法对510种化合物估算，在处理烷烃和烯烃时精度比较高，但估算包含多个卤原子的化合物偏差比较大[29]。

1.8 Wilson-Jasperson法

1996年，Wilson和Jasperson[30]提出了基于原子贡献的方法。

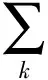
(9)

式中，Nr是化合物中环的数目；Nk是k类原子数；k类原子的一级原子贡献表示为Tck；Mj是j类基团数；j类基团的二级基团贡献表示为Tcj。

该方法能同时估算无机物和有机物，并且该方法无论是估算小分子还是大分子物质，误差都无显著差异，与文献实验值的比较结果见表4。由于没有全面考虑某些较突出的分子间力等的影响，导致该方法对有机酸和腈类的适用性很差，其计算值的误差是其它物质的两倍[23]。

表4数据显示该方法估算Tc是很精确的，二级基团贡献如果存在，通常情况下比一级原子贡献的估算有明显改进。

一级贡献法中，使用的是原子贡献、沸点和环状结构数，而二级贡献法只使用基团贡献。Wilson和Jasperson用该方法对700种各类化合物进行验算，其中包括172种无机气体、液体和固体、硅烷和硅氧烷。考虑到简单性和适用物质的广泛性，该方法比Joback法、G-G法、Marrero-Pardillo法更好，因为这种方法基团数最少，而且主要基于原子贡献，并同时适用于无机物和有机物[16]。

表4 Wilson-Jasperson法估算相关物质的Tc和文献实验值的比较结果[16]

1) 文献中可用于检验本方法的物质数量；2) AAE表示性质的平均绝对误差，A%E表示平均绝对百分比误差；3) 绝对百分比误差大于10%的物质数量；4) 绝对百分比误差小于5%的物质数量，误差在5%和10%之间的物质数量能由表中数据确定；5) 使用二级基团求性质的物质数量；6) 二级结果比一级更精确的物质数量；7) 与一级方法相比，二级方法的平均改进，负值表示总体上二级方法精度更低。

1.9 Marrero-Pardillo法

1999年，Marrero-Marejon和Pardillo-Fontdevila提出了该方法，称之为基团相互作用贡献法，或者更准确地讲为键贡献法[16]。

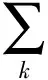
(10)

他们给出的方法使用由单一原子形成的原子对的值，或者是使用含氢的基团对的值。通过利用300多种物质的文献实验值与该法的估算结果进行比较，发现98%的物质的绝对百分比误差小于5%，且使用Tb的实验值计算得到的Tc比使用Tb估算值的结果更准确。Marrero-Pardillo法估算相关物质的Tc和文献实验值的比较结果见表5，碳原子超过3个的物质的Tc比较结果见表6。

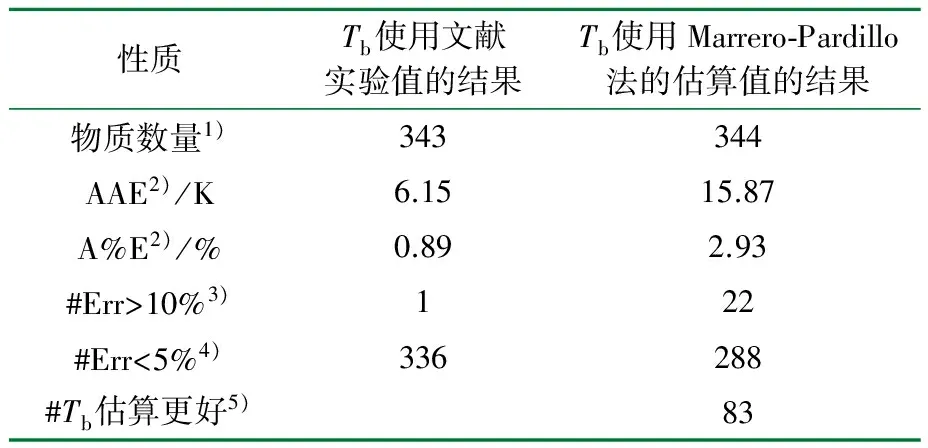
表5 Marrero-Pardillo法估算相关物质的Tc和文献实验值的比较结果[16]

1) 文献中可用于检验本方法的物质数量；2) AAE表示性质的平均绝对误差，A%E表示平均绝对百分比误差；3) 绝对百分比误差大于10%的物质数量；4) 绝对百分比误差小于5%的物质数量，误差在5%和10%之间的物质数量能由表中数据确定；5) 使用Tb估算值比使用实验值所得的Tc更精确的物质数量。

通过表4和表5比较得出，如果Tb有实验数据，Marrero-Pardillo法精确度比Wilson-Jasperson法更高。

表6 Marrero-Pardillo法估算碳原子超过3个的物质的Tc和文献实验值的比较结果[16]

1) 文献中可用于检验本方法的物质数量；2) AAE表示性质的平均绝对误差，A%E表示平均绝对百分比误差；3) 绝对百分比误差大于10%的物质数量；4) 绝对百分比误差小于5%的物质数量，误差在5%和10%之间的物质数量能由表中数据确定；5) 使用Tb估算值比使用实验值所得的Tc更精确的物质数量。

由表6可知，用Marrero-Pardillo法估算临界温度是非常可靠的，但大分子物质和小分子物质的误差有一些差别[16]。

Yan Xinjian等人用该方法对510种化合物进行估算，其精度比较好。但是其中有167种估算结果比Wilson-Jasperson法差[29]。

1.10 张克武-张宇英法

以Kirchhoff定律和钱学森推荐的特鲁顿定律建立的理论式作基础导出下式：

(11)

(12)

(13)

式中，ni为第i个基团(键或官能团)Ki的数目；ne为第e类电子效应(EF)Ke的数目。“基”与电子效应参数之和为KS，总称为分子结果参数。

公式(11)从烷烃导出结构参数理论值，可精确地推广到全部的有机物，表明理论预见性很强。通过42类406个纯物质Tc实测值验算，发现平均误差0.36%，误差在±1.0%的占总数的98%。他们对30种结构类型128个纯物质用Joback、MXXC和该方法进行计算。通过计算得到的Tc值与实验值进行比较得出结论：该方法的精度比Joback式高3.1倍，比MXXC式高6.7倍，而且Joback法对炔烃、醇、全氟碳化合物以及含多种卤的芳香族化合物的适用性较差[15]。

1.11 定位分布基团贡献方法

2008年，王强和马沛生等[31-33]论述了一个定位分布贡献方法理论。

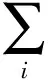
(14)

(15)

式中，T0为7 409.200 K；Ai、Aj为分基团i和j的贡献值；Ni为分子中以碳元素为中心的基团的数目；Nj为分子中以非碳元素为中心的基团的数目；N为分子中基团的数目；Pk为定位分布关联因子；a1，a2为模型参数；M为摩尔质量。

这是一个可预测碳链C2～C18有机化合物临界温度的新的简单可靠的方法。他们将此理论用于物性计算之中，成功解决了50多年来物性计算领域有机物的同分异构体无法区分的这一世界性难题。该方法的特点就是使用添加定位分布因子的定位分布函数来分辨大部分有机物cis-和trans-或Z-结构和E-结构的同分异构体。利用该方法对467种有机化合物进行验算，发现临界温度Tc的预测的总平均绝对差是6.6K和1.1%，而Joback法的结果是17.6K和3.1%、G-G法的结果是13.5K和2.3%，从而可以看出该方法更加准确。

1.12 其它方法

除以上几种方法外，估算有机物临界温度方法还有Liang-Ma法(L-M法)和Somayajulu法。

L-M法是20世纪90年代陆续发表的一些计算纯物质临界性质的基团贡献法中的一个。该方法的特点是修正了相邻基团的影响和区分了同分异构体。对大部分化合物进行估算时，二级贡献法的引入大大提高了精度。只用一级基团的平均误差为3.965%，而引入二级基团后的平均误差仅为0.756%[27]。在计算八种化合物的临界温度时，采用该方法比Lydersen法、Ambrose法和Joback法精度高很多[30]。

Somayajulu法是Rledel、Lydersen和Ambrose等方法的改进与完善，因此具有相似的校正项。在对C1～C10的51种烷烃进行检验的时候，该方法计算烷醇和卤代化合物比Ambrose法稍微简单一些。但当中心原子是N的时候，该方法不适用。通过利用该方法计算600多种化合物，其结果清楚地表明了非键合相互作用的重要性，但只是给出了误差分布，缺少总平均误差[34]。

2 不同基团贡献法估算松节油组分的临界温度

本课题组在松脂组分及其衍生物的热力学性质方面进行了大量研究[35-36]。松节油是松脂经过精馏以后得到的一种天然精油，有着广泛的用途，其主要组分包括α-蒎烯、β-蒎烯、β-石竹烯、β-水芹烯、三环烯等。伞花烃和柠檬烯是松节油主要异构化产物，而且是重要的化工原料之一。因此对上述物质的性质进行研究具有重要意义。

目前，松节油组分及其衍生物中，通过文献[37-38]能查到实验值的物质是α-蒎烯、Δ3-蒈烯、(+)-柠檬烯、伞花烃。分别用上述提到的方法进行计算并与文献实验值进行比较(公式里需要的Tb值来自于文献[37])，结果见表7。

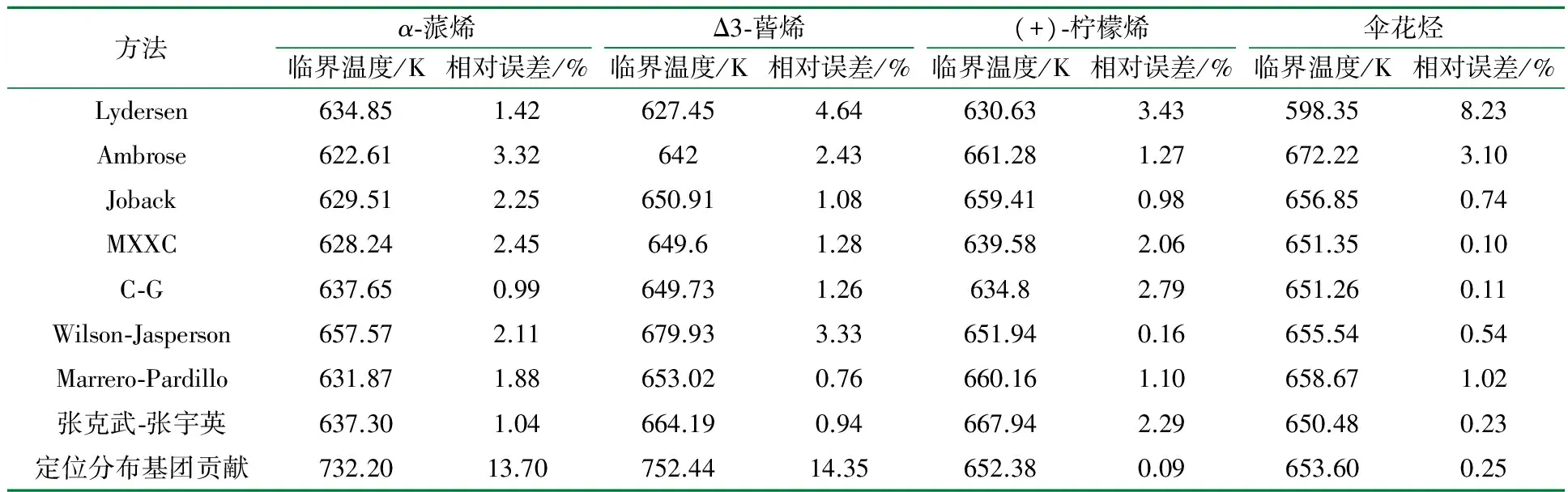
表7 不同基团贡献法估算上述4种物质的临界温度值和文献实验值比较的结果1)

1) 由于Riedel法基团划分比较简单及精度不高，而Fedors法适用于计算摩尔质量高或极不稳定而难于测定Tb的物质，所以这里不予以计算。

由估算结果可见，Joback、MXXC、Marrero-Pardillo、张克武-张宇英等方法用于该体系时相对误差在2.5%以下，比较适合用于该体系的估算。而Lydersen、Ambrose和Wilson-Jasperson等方法应用于该体系时相对误差较大，不推荐用于该体系的估算。定位分布基团贡献法由于缺少多元环的三环和四环的校正因子，估算α-蒎烯、Δ3-蒈烯的相对误差很大，而(+)-柠檬烯、伞花烃是单元环类化合物，估算的相对误差较小，都在0.25%以下，故该方法不适合用于多元环类化合物的估算。

3 结束语

综上所述，估算有机物临界温度的基团贡献法有很多，每种方法的适用范围和估算精度都有所不同，选用时应根据具体情况选择简单、精度高的方法。通常情况下，基团贡献法预测简单有机物时精度较高。由于基团贡献法中的官能团参数是从不完整的实验数据中拟合而得到的，且拟合而来的官能团参数并不适用于所有物系，因此基团贡献法的计算值与实验值存在一定的误差。对此，可从两方面进行改进来提高其计算精度：首先是不断完善实验数据和改进数值拟合方法；其次是深入研究原子、官能团以及分子之间的相互作用机理[39]。

随着计算机技术和量子力学的进步，将分子模拟应用于热力学计算，在量子理论的指导下以计算机进行分子模拟而得到相关的官能团参数并将其用于基团贡献法，以及将分子热力学微观层面的作用机制研究应用于基团贡献法将成为该领域关注的热点。

随着热力学性质估算工作进一步深入与研究，估算有机物临界温度的基团贡献方法也将不断完善和提高，使其具有更好的通用性和精确度，进而为化工生产、流程模拟、工程设计以及应用研究提供更加可靠的数据。

[1] 张克武，张宇英，张龙．临界性质研究领域的重大进展与临界温度的理论式的普适性[J]．黑龙江大学自然科学学报，2001，18(4)：67-76．

[2] 马沛生，夏淑倩，王新红，等．三种不稳定化合物临界温度和临界压力的测定[J]．化学工程，2004，32(5)：66-68．

[3] 梁英华，芮玉兰，马沛生．估算纯物质临界温度的新方法[J]．化工学报，2001，52(2)：146-152．

[4] 王新红，贾琦，高进，等．用简单物性估算纯物质临界参数的方法[J]．石油化工，2005，34(3)：254-257．

[5] VETERE A．Methods for the estimation of critical volumes[J]．Chemical Engineering Journal，1987，34(3)：151-153．

[6] 张红彦，马沛生．临界参数的估算方法[J]．化学工业与工程，2000，17(3)：149-154．

[7] RIAZI M R，DAUBERT T E．Simplify property prediction[J]．Hydrocarbon Processing，1980，59(3)：115-116．

[8] 童景山，高光华．应用低压下饱和液体PVT数据推算临界参数[J]．工程热物理学报，1994(4)：361-363．

[9] XU W，YANG Q．A new group contribution method for estimating critical properties of organic compounds[J]．Industrial & Engineering Chemistry Research，2001，40(26)：624-625．

[10] 张克武．物质的分子结构与临界温度的新关联式[J]．石油化工，1981(3)：193-199．

[11] 张克武．论物质的分子结构与临界温度[J]．化学学报，1984，42(12)：35-41．

[12] 陈钟秀，顾飞燕．化工热力学(第2版)[M]．北京：化学工业出版社，2006：270-290．

[13] 许文．估算有机物基础物性的新基团贡献法(Ⅱ)——基础物性的估算[J]．化学工程，1993(5)：50-54．

[14] SOMAYAJULU G R．Estimation procedures for critical constants[J]．J Chem Eng Data，1989，34(1)：106-120．

[15] 张宇英．分子热力学性质手册[M]．北京：化学工业出版社，2009：8-20．

[16] 波林．气液物性估算手册[M]．北京：化学工业出版社，2006：8-26．

[17] 王小艳．化工物性数据库系统软件开发[D]．青岛：青岛科技大学，2012．

[18] AMBROSE D，BRODERICK B E，TOWNSEND R．The critical temperatures and pressures of thirty organic compounds[J]．Journal of Applied Chemistry & Biotechnology，2007，24(6)：359-372．

[19] 童景山．流体的热物理性质[M]．北京：中国石化出版社，1996：100-331．

[20] KLINCEWICZ K M，REID R C．Estimation of critical properties with group contribution methods[J]．Aiche Journal，1984，30(1)：137-142．

[21] 许文．估算有机物基础物性的三基团参数关联式[J]．化工学报，1992，43(2)：222-229．

[22] FEDORS R F．A relationship between chemical structure and the critical temperature[J]．Chemical Engineering Communications，1982，16(1/6)：149-151．

[23] REID R C，PRAUSNITZ J M，POLING B E．The properties of gases and liquids[M]．4th．New York：McGraw-Hill，1986：38．

[24] JOBACK K G，REID R C．Estimation of pure-component properties from group-contribution[J]．Chemical Engineering Communications，1987，57(1/6)：233-243．

[25] CONSTANTINOU L，GANI R．New group contribution method for estimating properties of pure compounds[J]．Aiche Journal，1994，40(40)：1697-1710．

[26] MA P S，XU M，XU W，et al．New group-contribution correlations for estimation of critical properties[J]．Journal of Chemical Industry & Engineering，1990，5(2)：235-241．

[27] 董新法，方利国，陈砺．物性估算原理及计算机计算[M]．北京：化学工业出版社，2006：153-158．

[28] 于成峰，刘国杰．正常沸点下液体蒸发焓的基团贡献计算法[J]．化工学报，2001(6)：530-536．

[29] YAN X J，DONG Q，HONG X．Reliability analysis of group-contribution methods in predicting critical temperatures of organic compounds[J]．Journal of Chemical & Engineering Data，2003，48(2)：374-380．

[30] LIANG Y H，MA P S．A new group-contribution method for critical properties[J]．Chinese Journal of Chemical Engineering，2000，8(1)：78-83．

[31] WANG Q，MA P S，JIA Q Z，et al．Position group contribution method for the prediction of critical temperatures of organic compounds[J]．Journal of Chemical & Engineering Data，2008，53(5)：1103-1109．

[32] WANG Q，JIA Q Z，MA P S．Position group contribution method for the prediction of critical pressure of organic compounds[J]．Journal of Chemical & Engineering Data，2008，53(8)：1877-1885．

[33] JIA Q Z，WANG Q，MA P S．Position group contribution method for the prediction of critical volume of organic compounds[J]．Journal of Chemical & Engineering Data，2008，53(11)：1877-1885．

[34] SOMAYAJULU G R．New equations for enthalpy of vaporization from the triple point to the critical point[J]．International Journal of Thermophysics，1988，9(4)：567-575．

[35] 齐志文．左旋海松酸及其衍生物的单离和热力学性质研究[D]．昆明：昆明理工大学，2016．

[36] 张塞．二氢枞酸的分离提纯及其衍生物热力学性质研究[D]．昆明：昆明理工大学，2016．

[37] LIDDE D R．CRC handbook of chemistry and physics[M]．89th．Boca Raton：CRC Press/Taylor and Francis，2009：944-955．

[38] 马沛生．有机化合物实验物性数据手册[M]．北京：化学工业出版社，2006：287-288．

[39] 杨晓光，宋海华．基团贡献法的现状与展望[J]．石油化工，2003,32(增刊)：670-671．