离心力影响条件下的履带车滑移转向性能分析*

2017-03-15高学亮邓兆印

振动、测试与诊断 2017年1期

关键词：摩擦阻力离心力偏移量

董超, 成凯, 高学亮, 郗元, 邓兆印

(1.吉林大学机械科学与工程学院长春，130022) (2.吉林大学汽车仿真与控制国家重点实验室长春，130022)(3.长春发电设备总厂长春，130022)

离心力影响条件下的履带车滑移转向性能分析*

董超1, 成凯1, 高学亮2, 郗元1, 邓兆印3

(1.吉林大学机械科学与工程学院长春，130022) (2.吉林大学汽车仿真与控制国家重点实验室长春，130022)(3.长春发电设备总厂长春，130022)

针对传统履带车转向力学模型不考虑离心力的影响，为了准确计算履带车实际转向过程中的各个转向性能参数，在深入研究履带车转向机理的基础上，建立了综合考虑离心力和履带滑移/滑转等影响因素下的履带车转向数学模型，并以某一具体车型为例进行了数值求解。研究结果表明：车辆转向过程中产生的离心力会对转向性能产生影响，与传统转向模型分析结果相比，考虑离心力影响时的履带接地段压力呈现梯形状分布并非传统上认为的均匀分布；车辆在黏性度大的土壤上行驶时履带的滑移/滑转也会影响转向性能。实车试验也验证了模型的正确性。该研究成果为履带车的设计与优化以及平稳转向控制等提供理论依据。

履带车；离心力；转向半径；滑移率；驱动力

引言

履带行走系统作为特种工程车辆常采用的行走方式，因其具有良好的道路适应能力、高机动性以及优越的越野性能，被广泛运用于农业、林业、国防和建筑等领域。如何提高履带车的机动性能已经成为特种工程车辆技术革新的必然趋势[1-2]。其中，转向性能作为履带车机动性的一个重要标志，已经引起了广泛关注。目前，对履带车转向性能的研究方法大致分为两类：a.采用数学相关理论方法建立车辆转向模型进行求解分析，如：文献[3]建立了履带车转向性能预测模型；程军伟等[4]采用数学理论建立了履带打滑条件下的车辆转向模型；成凯等[5]建立了铰接式履带车行驶转向及车体作俯仰运动时的数学模型等；b.采用多体动力学仿真软件建立履带车的虚拟样机模型进行仿真分析，如：文献[6]采用Recurdyn软件建立了四履带车辆转向模型，通过虚拟样机仿真技术得到了车辆的驱动力随转向半径和履带宽度的变化规律；成凯等[7]利用Ansys软件对铰接式履带车处于转向工况条件下的关键零部件进行了有限元分析；马星国等[8]采用虚拟样机技术对高速履带车转向性能进行了仿真分析等。虽然上述研究取得了阶段性成果，但是建立的转向理论模型均未考虑离心力对车辆转向性能的影响。工程实践证明，履带车在实际转向过程中，车体产生的离心力严重影响车辆转向的平稳性，特别对于高速转向时此现象更为明显。因此，采用考虑离心力的转向模型来分析履带车的转向性能比传统方法具有现实意义。

笔者在研究履带车转向机理的基础上，建立了综合考虑离心力、履带滑移/滑转条件下的履带车转向数学模型，推导出履带车滑移转向过程中的各个运动学与动力学参数的计算公式。以某一具体车型为例进行了求解与试验,对比结果表明了所建模型的正确性。

1 履带车滑移转向过程中运动学关系

履带车差速转向时，车体绕转向中心Os匀速转向。理想情况下，内外两侧履带的速度瞬心Osi(i=1,2)与履带的几何中心Oi(i=1,2)重合,但实际转向时由于履带的滑移/滑转使履带的速度瞬心Osi(i=1,2)偏离履带的几何中心Oi(i=1,2)产生横向和纵向偏移量Ai和di(i=1,2)[9]。同时,转向过程中车辆作圆周运动产生的离心力FL使得车体质心Oc偏离车体的几何中心O产生横向和纵向偏移量Cx和Cy。离心力的横向分量影响着内外两侧履带的垂直载荷分配;离心力的纵向分量影响着履带纵向上的垂直载荷分配，如图1所示。运动学模型,图1中坐标系xOy为全局坐标系,OxOy为坐标原点;L,b,B分别为履带的长度和宽度以及车体的宽度;Os为车辆实际转向中心;Oc为车体的质心,车辆的实际转向半径R为转向中心Os到车体质心Oc的距离losoc;Osi(i=1,2)为内外两侧履带的速度瞬心;Oi(i=1，2)为内外两侧履带的几何中心;β为侧滑角。

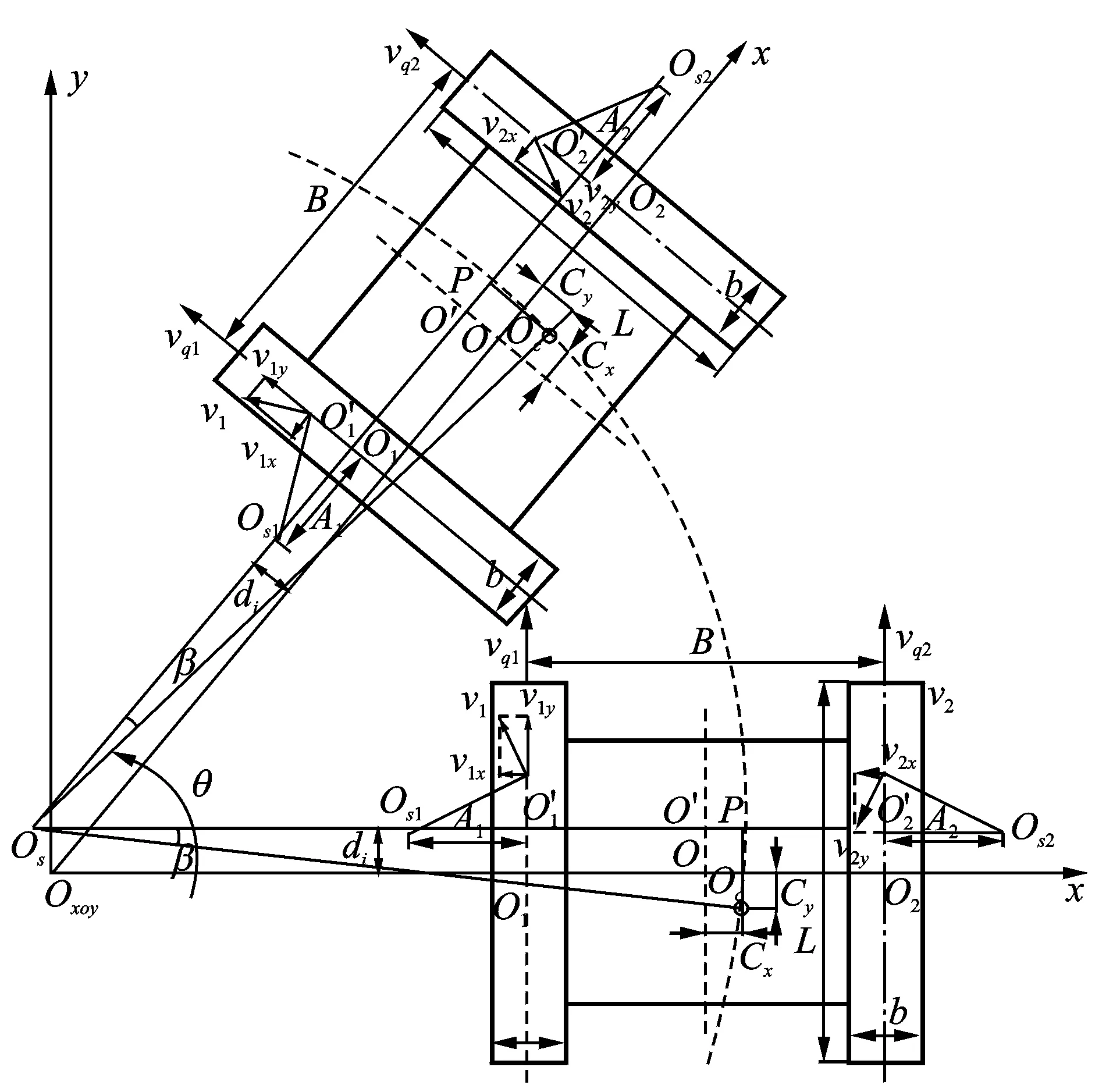
图1 履带车滑移转向运动学模型Fig.1 The caterpillar skid steer kinematic model

履带车转向时内外两侧履带中心线Oi′(i=1,2)处的牵引速度vo′i为

(1)

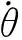
由于车辆转向过程中履带出现了滑移/滑转现象，因此履带仅有Oi′(i=1,2)处的卷绕速度与理论速度相等[10]，即

(2)

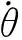
根据图1中的运动学关系可以求得履带在滑移/滑转条件下车辆的实际转向半径为

(3)

其中：D为车体质心Oc到转向中心Os的纵向垂直距离，D=Cy+di；Cy为车体质心的纵向偏移量;di(i=1,2)为内外两侧履带速度瞬心的纵向偏移量；losp可以根据式(2)求得。

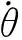
(5)

为了评价履带的滑移/滑转程度，笔者采用滑转率作为评价指标[11]，其表达式为

(6)

其中：vti为履带的卷绕速度;vo′i为内外两侧履带的牵引速度，可由式(1)求出。

将vti和vo′i代入式(6)，得到履带的滑转率δi为

(7)

2 履带车滑移转向过程中动力学关系

为了便于研究履带车滑移转向时运动学与动力学相关参数的变化规律，作如下假设：a.履带车在水平面内作匀速转向，且转向过程中车辆的行驶阻力系数保持不变;b.不考虑侧向土壤对履带产生推土阻力的影响;c.履带接地段压力分布呈连续线性分布，不计履带张力变化对接地段压力的影响。

2.1 履带接地段压力分布

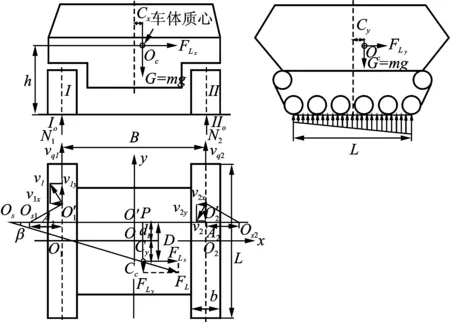
图2 离心力影响下的履带接地段压力分布情况Fig.2 The pressure distribution of track under the influence of the centrifugal force

履带车作圆周运动时常伴随离心力的产生，离心力不仅会影响履带接地段压力的分布,如图2所示,还会使车辆产生侧向力矩和横向摆动角,若车辆的横向摆动角过大,将严重影响行驶的稳定性。因此,在建立履带车转向动力学模型时,不可以忽视离心力的影响。根据图2,分别对履带受力点IO和IIO处列力矩平衡方程求得内外两侧履带法向垂直载荷N1和N2分别为

(8)

(9)

其中:v为车速;h为车体质心离地高度;R为转向半径;β为侧滑角;Cx为车体质心的横向偏移量；B为车体宽度；m为履带车的质量。

由式(8)，(9)可知，履带车滑移转向时产生的离心力使车体质心发生偏移，使得内侧履带法向载荷减小，外侧履带法向载荷增大。

内外两侧履带接地段压力为

其中：b为履带宽度；L为履带长度；N1，N2为内外两侧履带法向垂直载荷；Cy为车体质心的纵向偏移量；y1，y2为内外两侧履带接地段纵向上任意一点的纵坐标；D为车体质心Oc到转向中心Os的纵向垂直距离，D=Cy+di。

由式(10)与式(11)可知:履带车滑移转向时产生的离心力使履带接地段压力分布不均匀,前端接地压力减小,后端接地压力变大,总体呈现梯形状分布而不是传统上认为的矩形状均匀分布。

2.2 履带受到的转向摩擦阻力

车辆滑移转向时履带受到的行驶阻力主要来自地面的摩擦阻力。以履带的速度瞬心Osi为原点建立局部坐标系，x轴的正方向沿着履带的横向方向,y轴的正方向沿着履带的纵向方向，如图3所示。

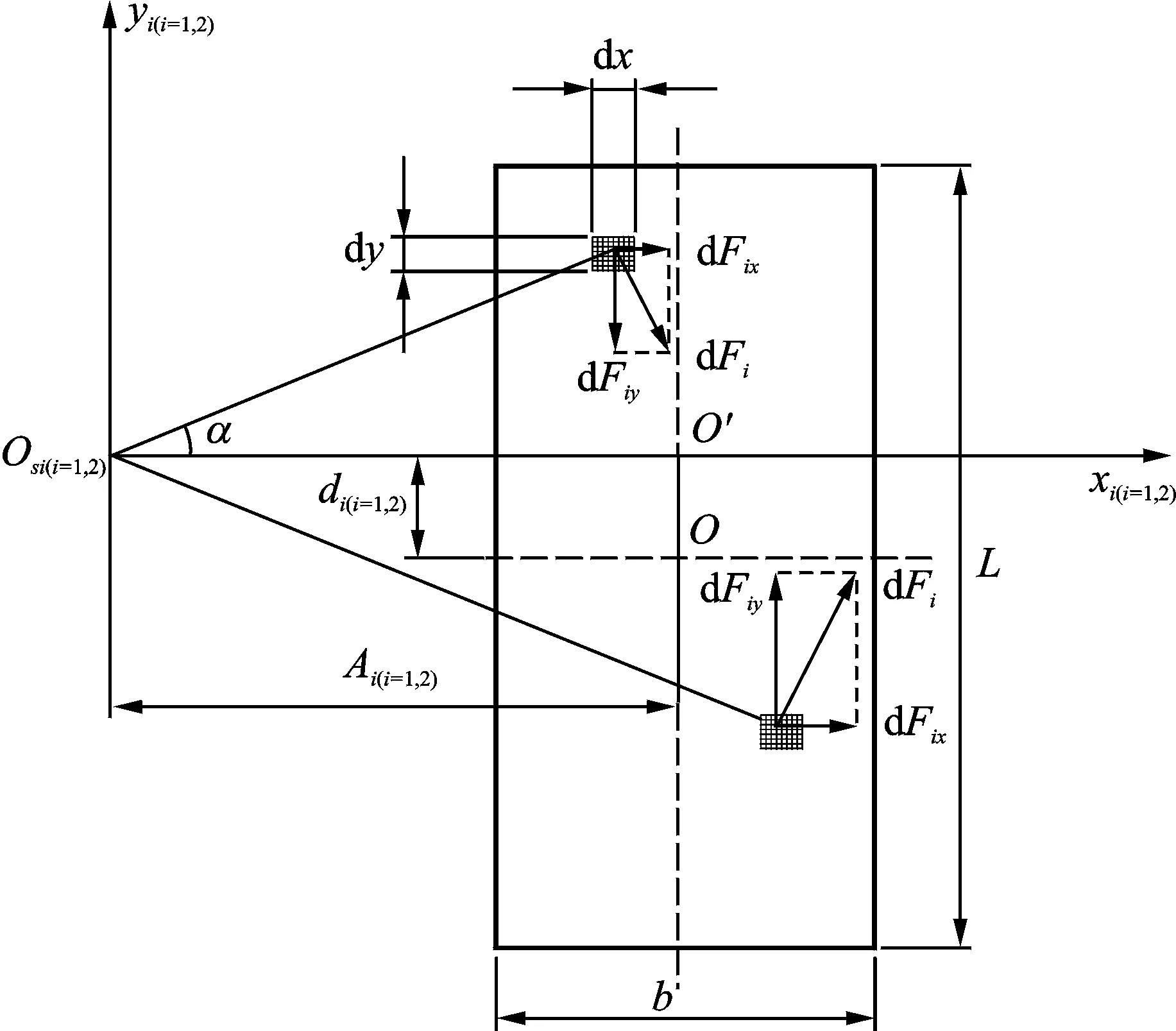
图3 履带接地段受到的地面摩擦阻力Fig.3 The friction resistance of the caterpillar

履带上任取一个微小单元，则车辆转向时地面对该微小单元产生的摩擦阻力在x轴、y轴上的分量为

dFx i=μpi(yi)sinα

(12)

dFy i=μpi(yi)cosα

(13)

其中:μ为摩擦因数；Pi(yi)(i=1,2)为履带接地段压力，可由式(10)，(11)求得；b，L为履带长度与宽度；α为微小单元与履带的速度瞬心之间的夹角。

对式(12)，(13)积分，得到地面对履带产生的摩擦阻力在x轴、y轴方向上的分量分别为

地面对履带产生的转向阻力矩为

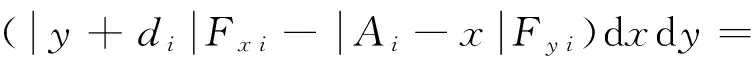
(16)

其中：b，L为履带的长度与宽度；Ai(i=1，2)为内外两侧履带速度瞬心的横向偏移量；di(i=1，2)为内外两侧履带速度瞬心的纵向偏移量；μ为摩擦因数；Pi(yi)为履带接地段压力。

2.3 履带受到的土壤沉陷阻力

根据Bekker土壤承载理论[12-13]，弹塑性土壤的变形量与土壤承载的关系为

(17)

履带车转向过程中，履带需要克服土壤沉陷量作功，履带克服土壤沉陷量作功为

(18)

对式(18)进行积分，求得履带车转向过程中履带克服土壤沉陷量所作的功为

(19)

根据功能原理Wi=FciL，得到车辆转向时履带所受到的土壤沉陷阻力为

(20)

其中：Z0为土壤的沉陷量；Kc为土壤内聚力模量；Kφ为土壤内摩擦力模量；n为土壤变形指数。

从式(17)，(20)可知：土壤的沉陷量和履带受到的土壤沉陷阻力是由履带的接地段压力和土壤的物理属性共同决定的，履带车滑移转向时产生的离心力使履带接地段压力分布不均匀，前端接地压力小，后端接地压力大，因此实际履带接地段的土壤沉陷量和受到的土壤沉陷阻力也是不均匀分布的，履带前端部分的土壤沉陷量和所受到的土壤沉陷阻力小于后端部分。

2.4 履带车滑移转向动力学模型

基于上述假设，履带车滑移转向时受到的阻力主要来自地面和车体内部。由式(14),(15)可知，影响车辆转向摩擦阻力的主要因素是履带的接地压力和摩擦因数。假设车辆转向过程中的地面摩擦因数不发生变化，这样决定车辆转向摩擦阻力的因素只有履带的接地压力。由于履带车滑移转向时产生的离心力使履带接地段压力前端小、后端大，导致履带受到的转向摩擦阻力呈不均匀分布，沿着履带纵向方向上的转向摩擦阻力以前端小、后端大的方式分布，如图3所示。沿履带横向方向上的转向摩擦阻力以梯形状方式分布，如图4所示。

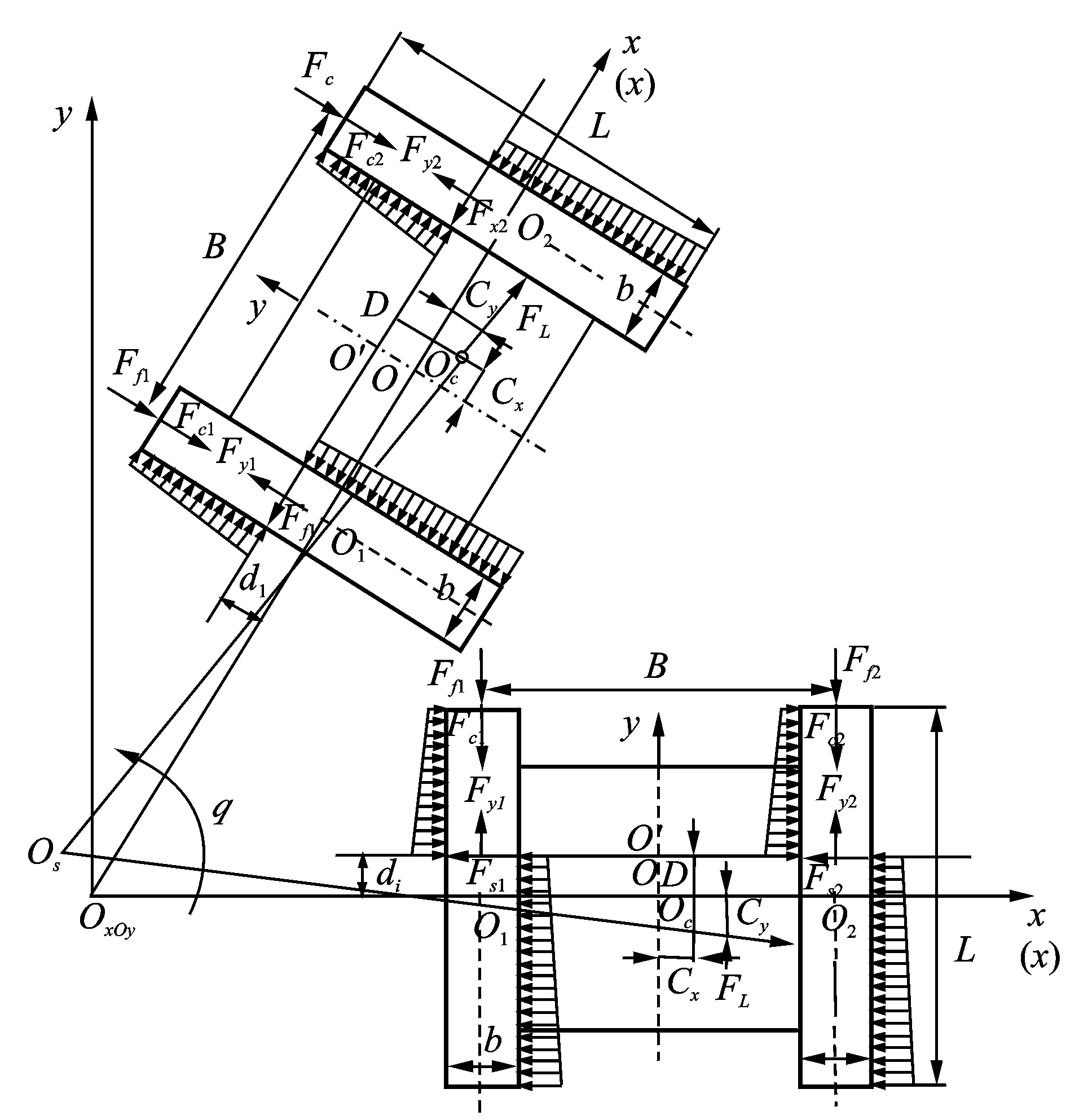
图4 履带车滑移转向动力学模型Fig.4 The caterpillar skid steer dynamics model

根据车辆平稳转向时履带受力平衡原理，得到平衡方程组为

(21)

其中:Fx1,Fx2,Fy1,Fy2为内外两侧履带受到的地面摩擦阻力在x轴、y轴方向上的分量；Fc1，Fc2为内外两侧履带受到的土壤沉陷阻力；β为侧滑角；D为车体质心Oc到转向中心Os的纵向垂直距离，D=Cy+di；v为车速；m为车辆质量；B为车宽；R为转向半径，根据式(4)求得；Mq1，Mq2为车辆转向时内外两侧履带所需要提供的驱动力矩，可以通过内外两侧履带纵向上所受到的力对O′取力矩求得；Ffi(i=1，2)为车体内部阻力，可根据Ffi=fNi，f=0.08求得，Ni可以根据式(8)与式(9)求得。

当给定车速、履带车的结构参数、内外两侧履带的牵引速度以及土壤参数时，采用数值迭代法可以求出式(21)中的3个未知数Ai(i=1,2)和di，进而得到履带车转向过程中的运动学和动力学参数。

3 实例分析

以国内某企业生产的履带车为例进行数值求解分析，选用车型结构尺寸如表1所示。设定车辆行驶路面为黏性土壤，物理参数[14]如表2所示。

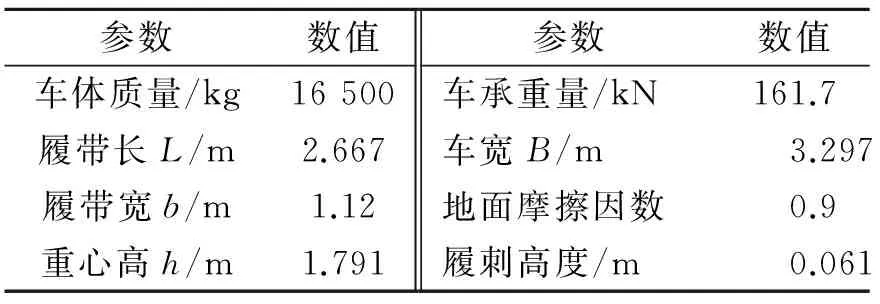
表1 履带车结构尺寸参数

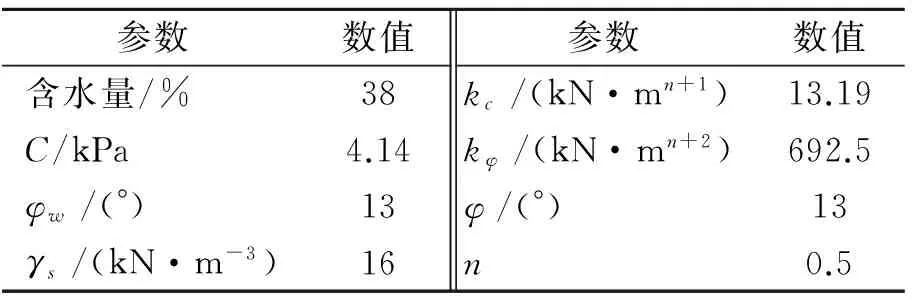
表2 黏性土壤参数[14]

将表1，2中的参数代入式(1)～(21)，求得履带车转向过程中运动学和动力学相关参数的变化规律。

3.1 履带车滑移转向过程中的运动学分析

3.1.1 车体质心偏移与履带的速度瞬心偏移对车辆转向半径的影响

图5为车体质心偏移对转向半径的影响。可以看出：车体质心偏移会对转向半径产生一定的影响，随着车体质心横向偏移量的增加，转向半径也增加且呈现线性增加的趋势；随着车体质心纵向偏移量的增加，转向半径也增加，但是其增加趋势表现为非线性增加。此外，车体质心横向偏移量对转向半径的影响效果大于纵向偏移量对其的影响效果。

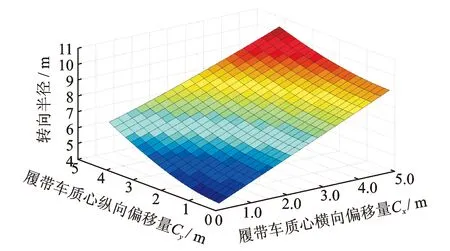
图5 车体质心偏移量对转向半径的影响Fig.5 Tracked vehicle centroid offset affects turning radius

图6为履带的速度瞬心偏移对转向半径的影响。可以看出：内外两侧履带的速度瞬心横向偏移均会对转向半径产生影响，随着内侧履带的速度瞬心横向偏移量的增加，履带车的转向半径逐渐减小且呈现非线性减小的趋势；随着外侧履带的速度瞬心横向偏移量的增加，履带车的转向半径逐渐增加，呈现出线性增加的趋势。

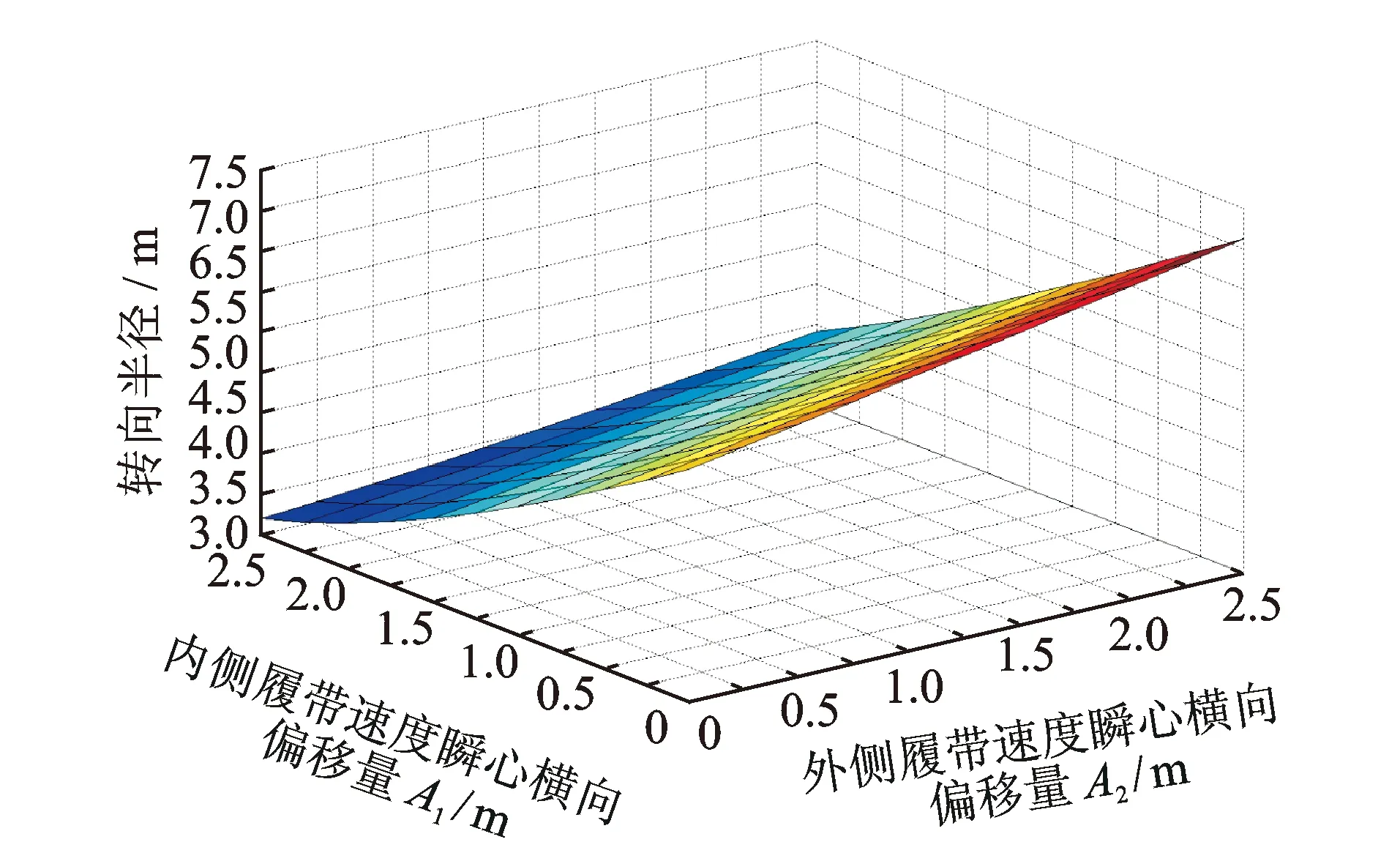
图6 履带的速度瞬心偏移量对转向半径的影响Fig.6 The crawler instantaneous offset affects turning radius

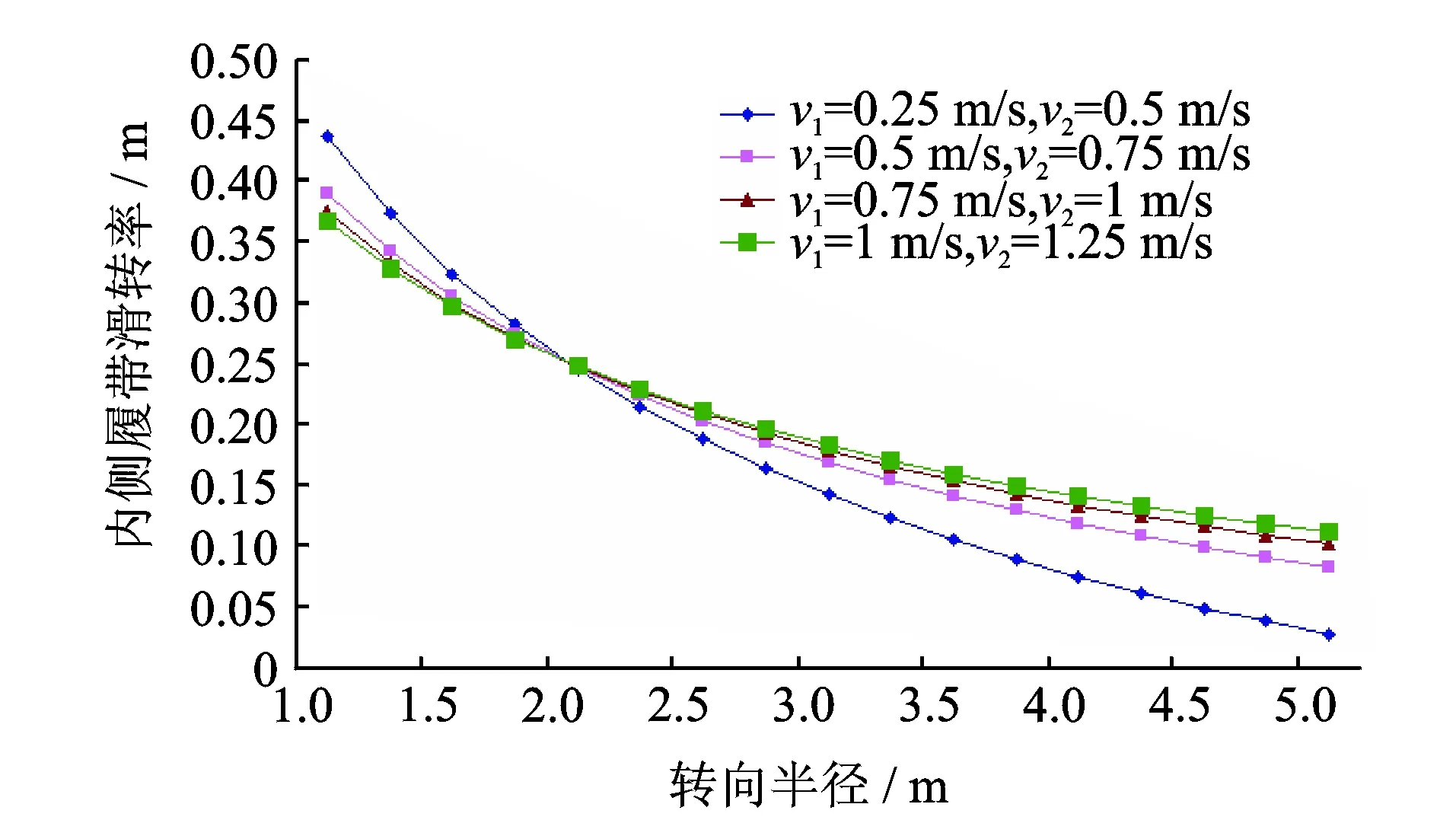
图7 不同车速和转向半径下内侧履带滑转率变化曲线Fig.7 The lateral slip rate change curve of insides crawler under different speed,different turning radius

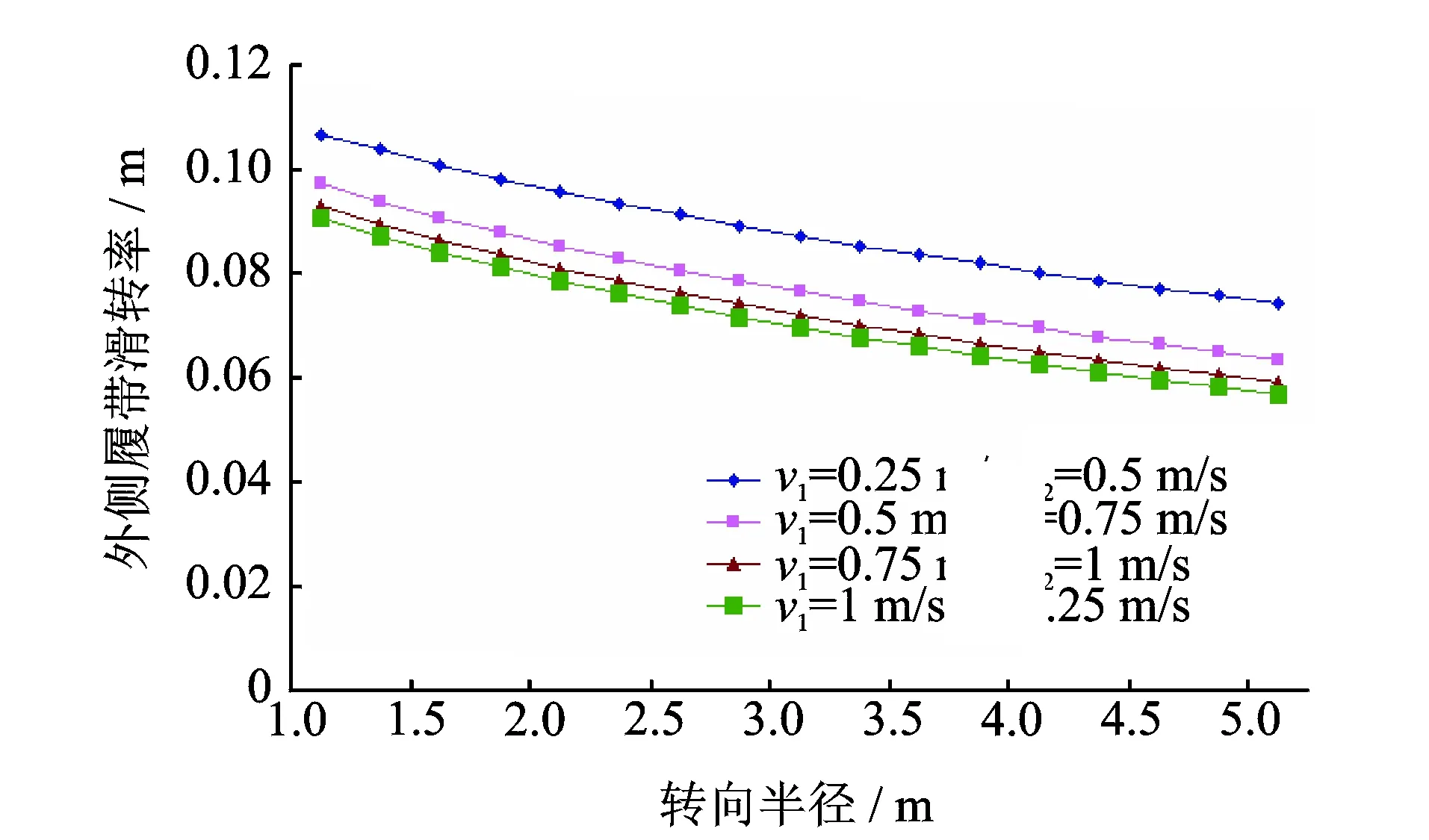
图8 不同车速和转向半径下外侧履带滑转率变化曲线Fig.8 The lateral slip rate change curve of outsides crawler under different speed,different turning radius

3.1.2 不同车速和转向半径条件下内外两侧履带滑转率的变化规律

图7和图8为不同车速和转向半径与内外两侧履带滑转率之间的变化关系。可以看出：随着转向半径的增加，内外两侧履带的滑转率均减小，但是内侧履带的滑移现象要比外侧履带的滑移现象更为严重，并且内侧履带的滑转率下降程度大于外侧履带的滑转率下降程度。履带车采用高速行驶时，车速对履带滑转率的影响效果较小。履带车低速行驶时，车速对履带滑转率有较大的影响。

3.2 履带车滑移转向过程中的动力学分析

3.2.1 履带车滑移转向时内外两侧履带接地段压力分布特性

从式(10),(11)可以看出：内外两侧履带接地段压力是关于履带纵向长度yi(i=1,2)的函数，为了研究履带接地段的压力分布特性，笔者以计算主动轮、7个支重轮和导向轮接地中心处的压力为例进行论述。选用的分析样车履带结构布置形式如图9所示。

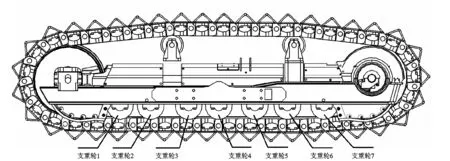
图9 履带结构示意图Fig.9 The track structural of vehicle

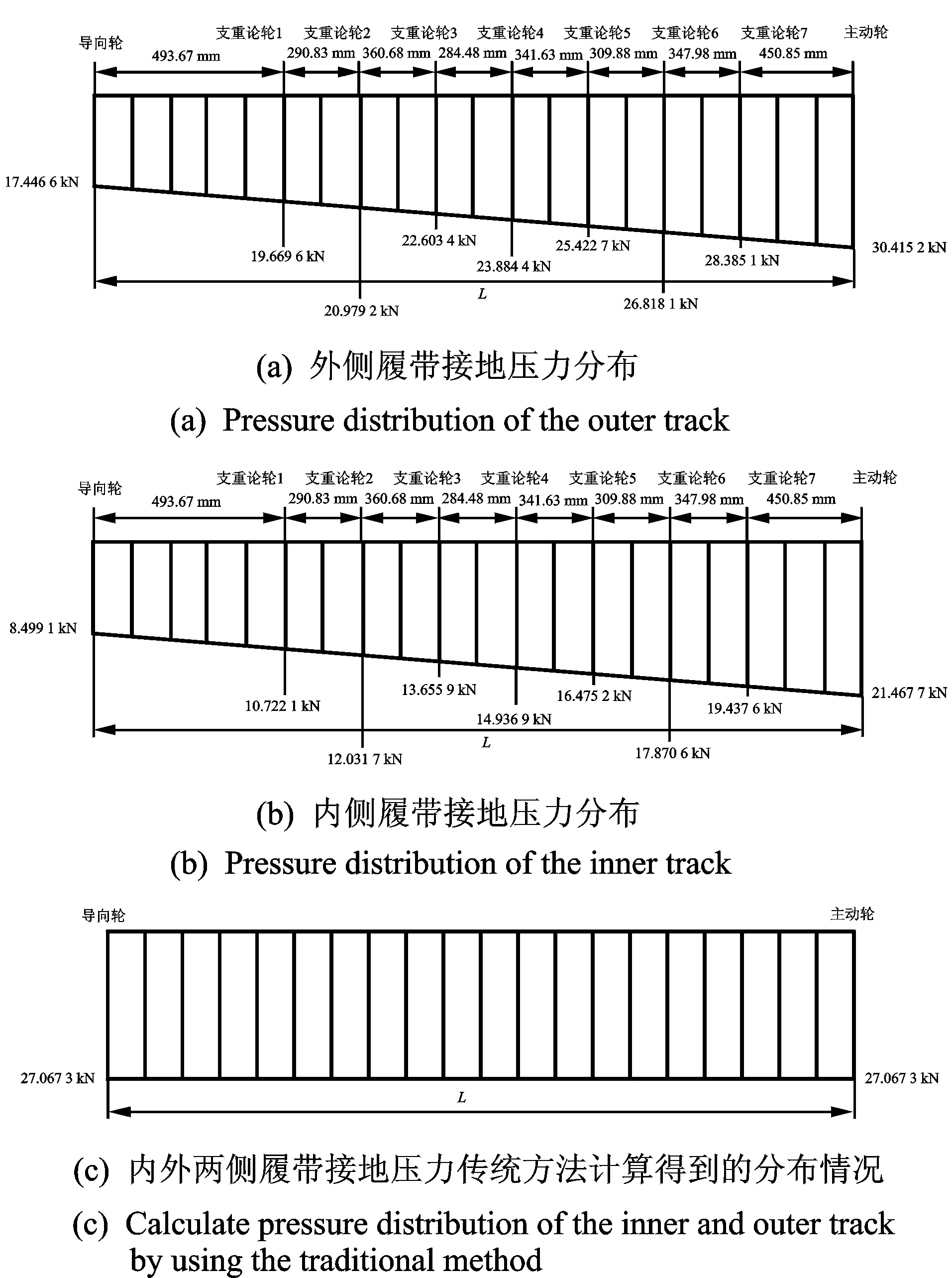
图10 内外两侧履带接地压力分布状态Fig.10 The pressure distribution of the both sides of the track

图10为履带车在车速v=2 m/s，转向半径R=5 m的条件下内外两侧履带接地段压力分布特性。可以看出：a.车辆转向时内外两侧履带接地段压力分布不均匀，外侧履带接地段压力总体大于内侧履带接地段压力，这是由于车辆转向过程中产生的离心力使车体质心向外偏离，引起外侧履带法向载荷增大，内侧履带法向载荷减小；b.同一履带沿纵向方向上的接地段压力分布也不是均匀的，而是履带前端接地段压力小，后端接地段压力大，总体呈现出梯形状分布形式，不是传统上认为的矩形状分布，造成这一现象的原因是车辆转向过程中产生的离心力使车体质心向车尾偏移，引起履带前端接地段压力减小，后端接地段压力增大。

3.2.2 履带的速度瞬心偏移对转向摩擦阻力影响

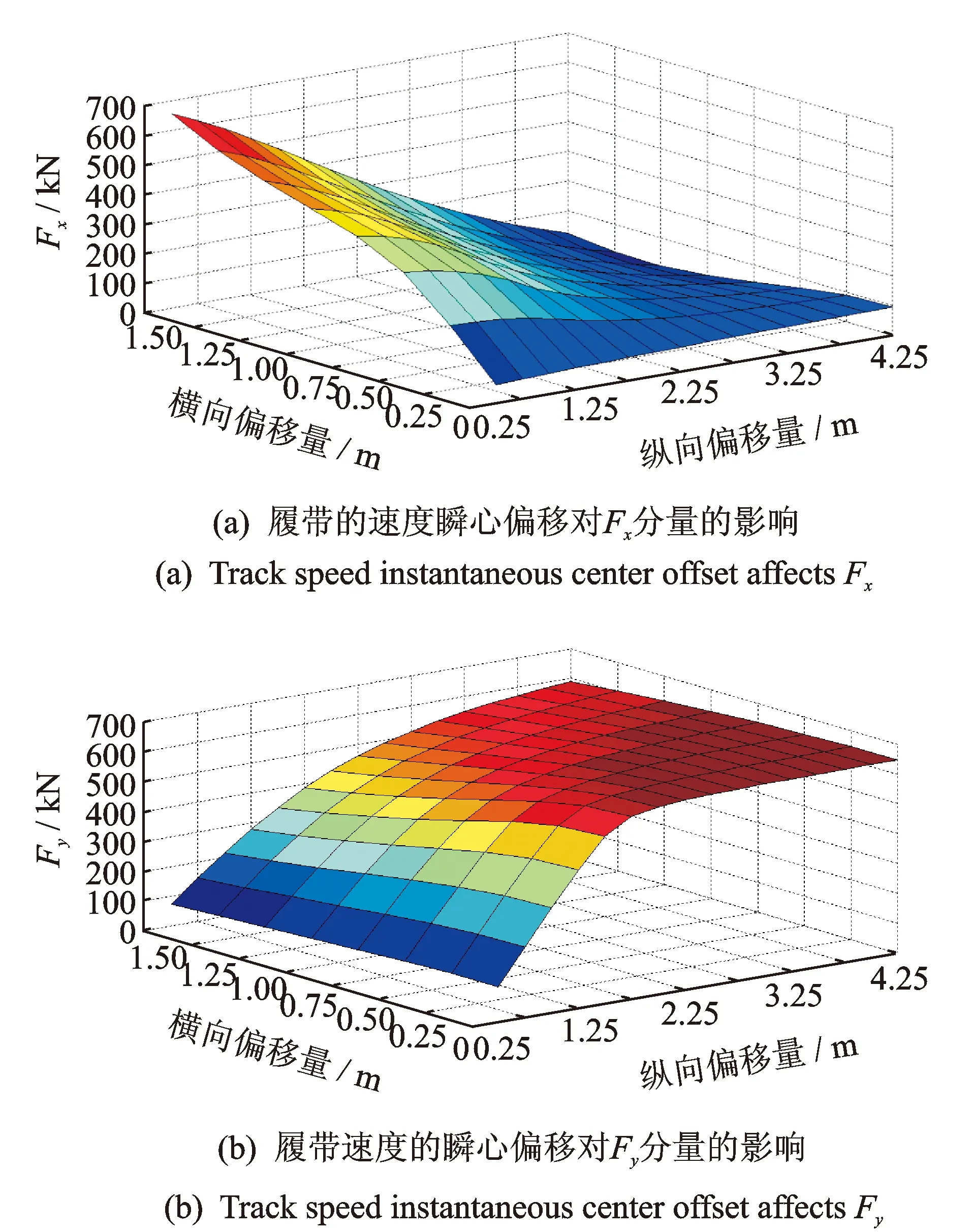
图11 履带的速度瞬心偏移对转向摩擦阻力的影响Fig.11 Track speed instantaneous center offset affects the steering friction

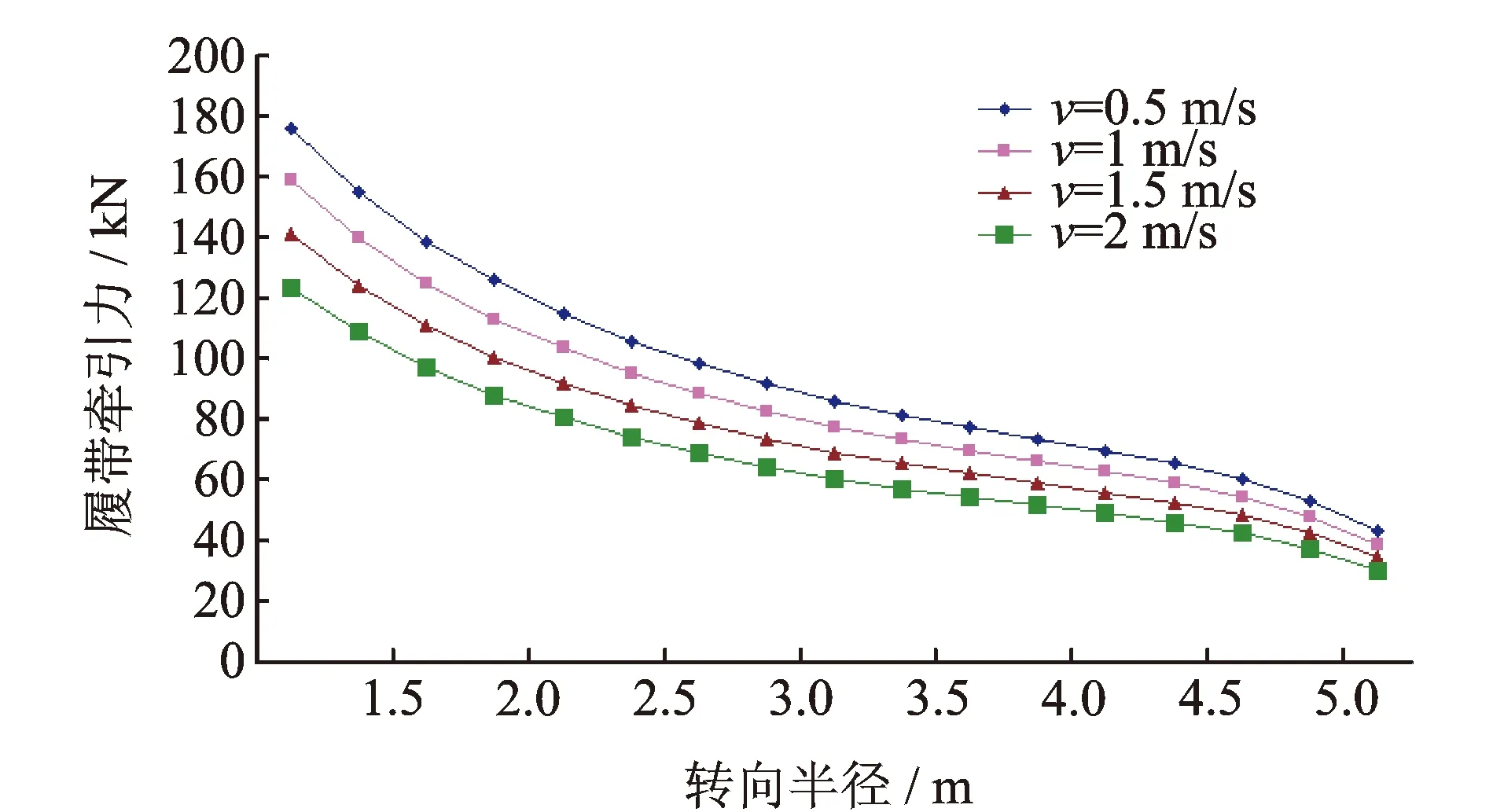
图12 不同车速和转向半径条件下履带牵引力变化曲线Fig.12 The traction change curve of crawler under different speed and different turning radius

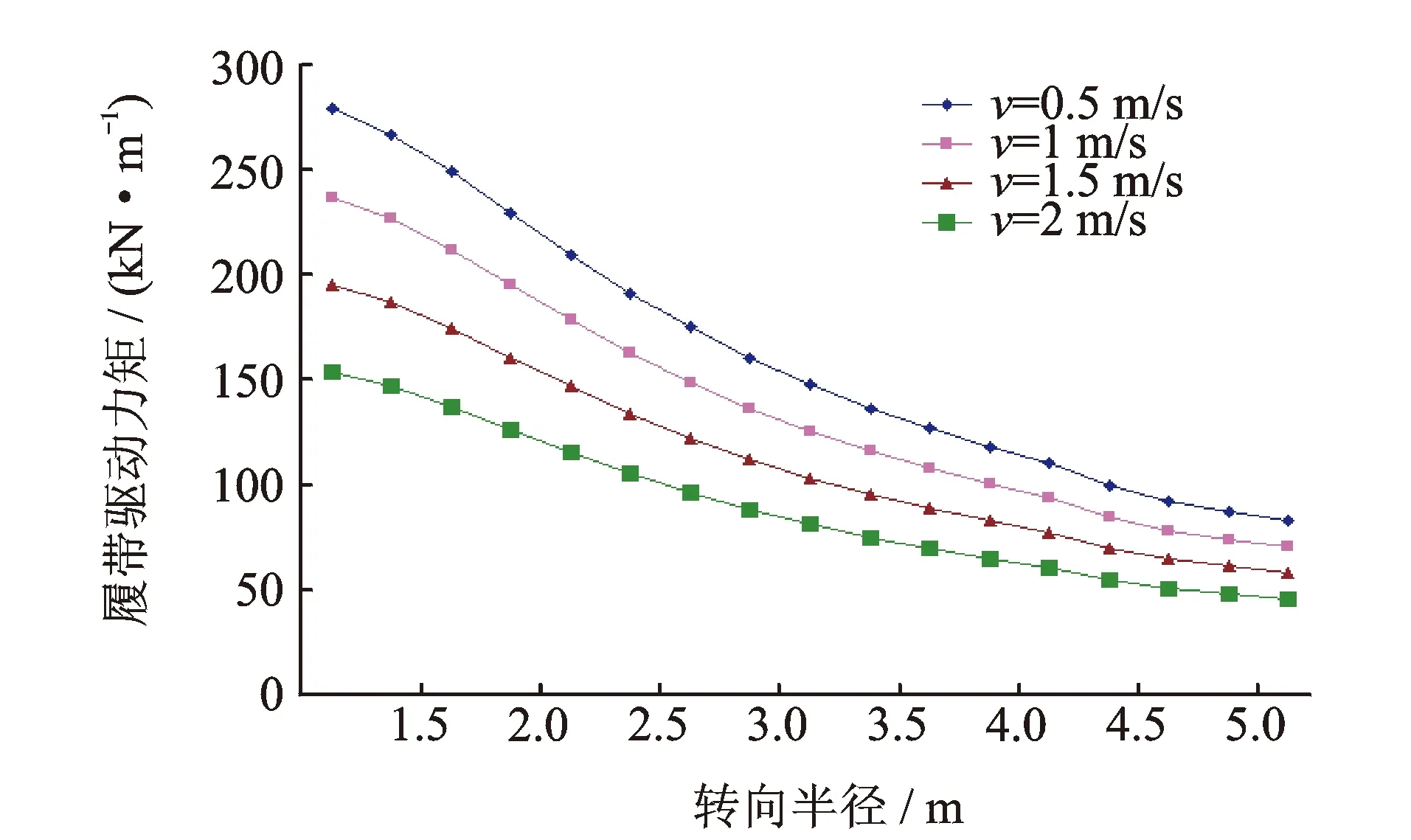
图13 不同车速和转向半径条件下履带驱动力矩变化曲线Fig.13 The driving torque change curve of crawler under different speed and different turning radius

图11为履带的速度瞬心偏移对转向摩擦阻力的影响。从图11(a)可看出：履带速度瞬心的横向偏移量与纵向偏移量均会对转向摩擦阻力在x方向上的分量Fx产生较大影响，随着横向偏移量的增加，Fx值增大；随着纵向偏移量增加，Fx值减小。从图11(b)可看出：转向摩擦阻力在y方向上的分量Fy随纵向偏移量的增加而减小，随横向偏移量的增加而增大。但是横向偏移量对Fy的影响效果更加明显，随着横向偏移量的增加，Fy值急剧增加且增长幅度较大，当横向偏移量达1.75 m时，Fy值逐渐趋于稳定状态。可见：履带的速度瞬心偏移对转向摩擦阻力有较大的影响，这说明履带的滑移/滑转对车辆的转向性能有较大的影响，因此在建立履带车转向力学模型时不可以忽略履带的滑移/滑转。

3.2.3 不同车速和转向半径条件下履带的牵引力和驱动力矩的变化规律

图12，13为车辆在不同车速和转向半径条件下履带的牵引力和驱动力矩的变化曲线。可以看出，随着转向半径的增加，履带的牵引力和驱动力矩均减小，这与文献[15-16]的研究结果一致。从图12可知：随着车辆转向半径的增加，履带的牵引力逐渐减小；在离心力的影响下，车辆处于高速转向时履带的牵引力比处于低速转向时的小；车辆处于小半径转向时，由于受到离心力的较大影响，使履带的牵引力发生了较大变化。从图13可知：履带的驱动力矩随着转向半径的增加而减小，并且车速对履带的驱动力矩有较大的影响效果。从式(21)可知:履带车的结构尺寸、行驶路况、转向半径和车速等都是影响牵引力和驱动力矩的因素。

4 试验验证

为了验证建立的履带车转向数学模型的正确性，以某一履带车为例进行实车试验,试验样车如图14所示。试验场地选择黏性土壤，试验过程中车辆以II档(v=7.2 km/h)的速度匀速稳态转向，整个试验过程中特别要求发动机始终近似处于匀速稳定运转。

采用基于光电传感器的转速测量系统测量内外两侧履带主动轮的转速，测量结果分别为vq1=1.86 m/s,vq2=2.78 m/s；动力输出轴两侧安装盘式转矩传感器测量转矩,该传感器具有存储数据功能；采用基于GPS的车辆行驶轨迹测量系统测量车辆的转向轨迹和转向速度等;采用电子罗盘测量车辆的转向角度，整个试验过程中数据采集由NI公司生产的数据采集系统完成。试验测量结果与理论计算值对比如表3所示。

图14 试验选用的样车Fig.14 The selected tracked vehicle for test

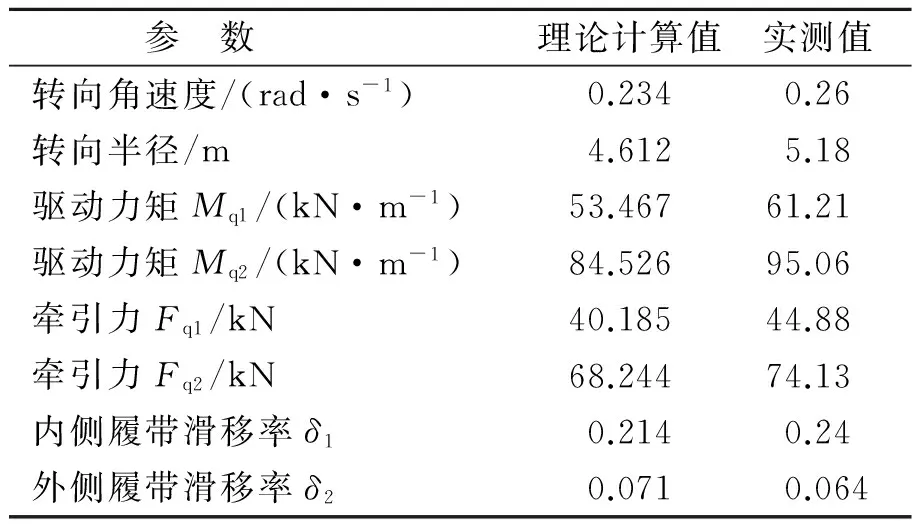
参数理论计算值实测值转向角速度/(rad·s-1)0.2340.26转向半径/m4.6125.18驱动力矩Mq1/(kN·m-1)53.46761.21驱动力矩Mq2/(kN·m-1)84.52695.06牵引力Fq1/kN40.18544.88牵引力Fq2/kN68.24474.13内侧履带滑移率δ10.2140.24外侧履带滑移率δ20.0710.064

可以发现:理论模型的计算值与试验测量值之间的误差不超过15%，说明计算结果与实测结果较为接近，验证了所建模型的正确性。

5 结论

1) 在综合考虑离心力和履带滑移/滑转对车辆转向性能影响的前提下，建立了履带车滑移转向数学模型，理论计算结果与实测结果相符表明了所建模型的正确性，可用于研究履带车滑移转向过程中运动学与动力学相关参数的变化规律，为履带的优化与设计以及控制车辆平稳转向等提供理论参考。

2) 利用所建模型对车辆转向性能分析结果表明：车辆转向时产生的离心力对履带的接地压力、驱动力及驱动力矩有较大影响，尤其对于高速行驶的履带车而言此现象更为突出，所以在研究履带车转向相关问题时和履带车实际设计过程中不可以忽略离心力的影响。

3) 对车辆转向过程中转向半径和转向摩擦阻力的变化规律分析表明：车辆在黏性土壤上行驶时履带的滑移/滑转对转向性能有明显影响，土壤黏性度越大，影响程度越大。因此在对履带车转向性能分析时应明确行驶路况，对于黏性度小的路况可以不计履带滑移/滑转的影响，但对于黏性度大的路况，此处理不妥。

[1] Janarthanan B，Padmanabhan C，Sujatha C.Longitudinaldynamics of a tracked vehicle:simulationand experiment[J].Journal of Terramechanics，2012,49(2)：63-72.

[2] 苏忠亭，徐达，王帅帅.步兵战车车体结构有限元模型修正[J].振动、测试与诊断,2014,34(6):1148-1153.

Su Zhongting,Xu Da,Wang Shuaishuai.Finite-element model updating for infantry combat vehicle car-body[J].Journal of Vibration,Measurement & Diagnosis,2014,34(6):1148-1153.(in Chinese)

[3] Maclaurin B.A skid steering model using the magic formula[J].Journal of Terramechanics，2011,48:247-263.

[4] 程军伟，高连华，王红岩.基于打滑条件下的履带车辆转向分析[J].机械工程学报，2006,42(S):192-195.

Cheng Junwei,Gao Lianhua,Wang Hongyan.Steering analysis of tracked vehicles based on skid condition[J].Chinese Journal of Mechanical Engineering, 2006,42(S):192-195.(in Chinese)

[5] 成凯，张俊，曲振东.铰接履带车转向及俯仰性能研究[J].兵工学报,2012,33(2)：134-141.

Cheng Kai，Zhang Jun，Qu Zhendong.Research on the turning and pitching performances of articulated tracked vehicle[J]. Acta Armamentarii, 2012,33(2)：134-141.(in Chinese)

[6] 李勇，姚宗伟，王国强.四履带车辆转向性能仿真研究[J].农业机械学报，2011，42(2)：34-38.

Li Yong,Yao Zongwei,Wang Guoqiang.Steering performance simulation of four-tracked vehicle[J].Transactions of the Chinese Society for Agricultural Machinery，2011，42(2)：34-38.(in Chinese)

[7] 成凯，魏小强，李贵助.铰接履带式运输车转向俯仰装置强度刚度分析[J].长安大学学报：自然科学版，2013，33(2)：95-100.

Cheng Kai，Wei Xiaoqiang,Li Guizhu.Strength and stiffness analysis of articulated steering and pitching device on the all-terrain articulated tracked carrier[J].Journal of Chang′an University： Natural Science Edition,2013，33(2)：95-100.(in Chinese)

[8] 马星国，余昊，尤小梅，等.油气悬挂式履带车辆高速转向动力学仿真[J].中国工程机械学报，2014,12(3):229-232.

Ma Xingguo,Yu Hao,You Xiaomei,et al.Dynamical simulation on high-speed steering for oil-gas-suspended tracked vehicles[J].Chinese Journal of Construction Machinery，2014,12(3):229-232.(in Chinese)

[9] 胡际勇.重型履带车辆软地面行驶性能研究[D].长春：吉林大学，2012.

[10]王红岩,王钦龙,芮强.高速履带车辆转向过程分析与试验验证[J].机械工程学报，2014,50(16):162-171.

Wang Hongyan,Wang Qinlong,Rui Qiang,et al.Analyzing and testing verification the performance about high-speed tracked vehicles in steering process[J].Chinese Journal of Mechanical Engineering,2014,50(16):162-171.(in Chinese)

[11]张克健.车辆地面力学[M].北京：国防工业出版社，2001.

[12]Bekker M G.Introduction to terrain-vehicle systems[M].Ann Arbor:University of Michigan Press，1969.

[13]Quynh L V，张建润，刘晓波，等.振动压路机用于不同土壤地面的平顺性评价[J].农业工程学报，2013,29(9)：39-47.

Quynh L V,Zhang Jianrun, Liu Xiaobo,et al. Ride comfort evaluation of vibratory roller under different soil ground[J].Transactions of the Chinese Society of Agricultural Engineering, 2013,29(9):39-47.(in Chinese)

[14]左鹏.全地形铰接履带车行走系统研究[D].长春：吉林大学,2012.

[15]Merhof W,Hackbarth E M.履带车辆行驶力学[M].北京：国防工业出版社，1989.

[16]Al-Milli S,Seneviratne L D, Althoefer K.Track-terrain modelling and traversability prediction for tracked vehicles on soft terrain[J].Journal of Terramechanics,2010,47(3):151-160.