基于MED和SK的滚动轴承循环冲击特征增强*

张 龙, 胡俊锋, 熊国良

(华东交通大学机电与车辆工程学院 南昌， 330013)

基于MED和SK的滚动轴承循环冲击特征增强*

张 龙, 胡俊锋, 熊国良

(华东交通大学机电与车辆工程学院 南昌， 330013)

提出了一种融合最小熵解卷积(minimum-entropy deconvolution, 简称MED)和谱峭度(spectral kurtosis, 简称SK)的轴承循环冲击类故障检测方法。利用最小熵解卷积得到消噪信号，若能检测到轴承故障特征则完成诊断过程，否则对消噪信号进行谱峭度分析选取最佳滤波器参数，对滤波信号进行二次滤波。通过包络谱检测确定是否存在故障及故障类型。实验室信号及工程案例的分析结果验证了该方法在检测轴承局部故障中的有效性和优越性。

共振解调；谱峭度；最小熵解卷；故障诊断

引 言

滚动轴承是旋转机械中应用最广泛也最容易损坏的机械零部件之一。轴承故障会导致机械设备出现不同程度的振动与噪声，其运行状态将直接影响到整台设备的性能[1]。因此，滚动轴承的故障状态监测与诊断一直都是人们研究的重要方向[2]。

在滚动轴承故障诊断中，共振解调法是目前运用最广泛的方法之一。它利用带通滤波器将低频干扰与噪声滤除，使故障冲击特征增强，从而便于确定轴承是否存在故障以及故障类型。然而带通滤波器参数的选择往往需要丰富的经验及大量的历史实验数据，且不同的参数选择对分析结果有非常大的影响，在获得满意结果前需要进行多次尝试，操作人员主观影响大。

盲信号处理(blind signal processing, 简称BSP)技术是在通信系统、图像处理和生物医学等领域已成功应用[3]。近年来，BSP技术在故障诊断领域的研究和应用已成为一大热点。盲解卷积作为BSP技术的研究方向之一，受到广大学者的关注。Wiggins[4]提出了最小熵解卷积方法，将最小熵方法应用于盲解卷积问题处理中。MED最早被应用于地震信号处理，并迅速拓展到其他领域。文献[5] 将小波变换与MED结合应用于网络故障的特征提取。文献[6]将最小熵解卷积方法引入管道的超声检测领域。文献[7]将最小熵解卷积和支持向量机结合应用于齿轮箱的故障诊断。文献[8]利用自回归(autoregressive,简称AR)模型消除齿轮啮合时产生的背景噪声,再对滤波信号进行最小熵解卷积以增强冲击特征。最小熵解卷积方法在轴承故障诊断领域取得了良好的应用效果，但对于强噪声环境下的滚动轴承微弱故障信号仍然存在故障冲击特征难以提取等问题。

为了增强滚动轴承循环冲击类特征提取效果，提高轴承局部故障的检测效率，笔者提出了一种联合最小熵解卷积和谱峭度的滚动轴承局部故障循环冲击特征增强方法。利用最小熵解卷积方法对故障信号进行滤波和包络谱分析。若能提取出故障特征频率则完成诊断过程，若诊断效果不佳，以谱峭度方法设计最优带通滤波器对滤波信号进行二次噪声消除，通过包络谱分析确定故障特征频率。最后利用实验数据及工程应用实例对所提方法进行了验证。

1 滚动轴承循环冲击特征增强方法

在机械故障诊断中，最小熵解卷积对于强噪声信号的诊断效果并不十分理想，对滤波信号采取一定的后处理手段能够进一步提高诊断效果。最小熵解卷积方法在故障特征提取过程中对信号进行盲解卷积，进而消除传递路径的影响，从噪声信号中提取出故障冲击特征[8]。MED结合谱峭度消除测量噪声和环境干扰的能力将获得更好的效果。

笔者提出的基于MED和SK的滚动轴承故障诊断方法流程如图1所示。利用MED消除传递路径对冲击特征的衰减作用，若MED消噪后信号包络谱中能够找到故障特征频率，则结束诊断，无需进行二次滤波以节省计算资源和时间。若测量噪声和环境干扰作用仍然较大，从MED包络谱中无法检测到明显的故障频率，则利用谱峭度方法对MED消噪信号进行二次滤波并得到包络谱，从包络谱中判断故障有无及故障类型。

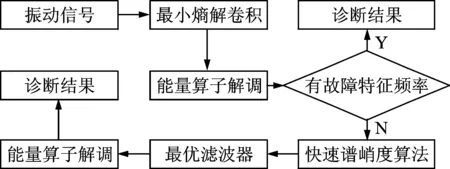
图1 基于MED和SK的轴承故障检测流程图Fig.1 The procedure of bearing defects using MED and SK

1.1 最小熵解卷积

最小熵解卷积[4]的基本原理在于利用最小熵能使尖锐脉冲特征得到增强的特性设计最优滤波器，使滤波后信号的脉冲冲击成分得到增强，计算终止条件为最大峭度值[9]。最小熵解卷积方法最早被应用于地震波反射参数提取，并逐渐拓展到其他领域。

y(n)=h(n)*x(n)+e(n)

(1)

其中：y(n)为输出；h(n)为传递函数；x(n)为输入；e(n)为噪声。

解卷积问题的目的在于寻找一个K阶的最优逆滤波器g(n)，使经过g(n)后的y(n)能够恢复x(n)的各项特征。

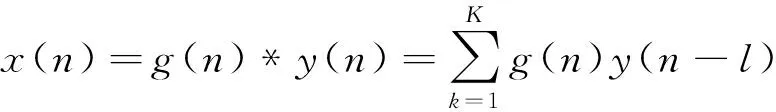
(2)

其中：K为逆滤波器g(n)的长度 ，对两边求导

(3)

在恢复输入x(n)时，重点是利用逆滤波器g(n)使输入x(n)恢复原有信号含有的简单特征及相关信息，使熵值最小,因此被称为最小熵解卷积。

(4)

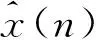
(5)

联合式(2)得

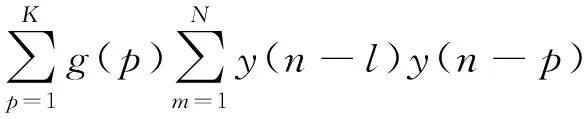
(6)

式(6)写成矩阵形式为

f=Ag

(7)

其中：A为序列y(n)的K×K自相关矩阵；f=(f(l))T。

f(l)表示为

(8)

其中

(9)

式 (6)经过迭代可得到逆滤波器矩阵为

g=A-1f

(10)

1.2 谱峭度

谱峭度最早由Dwyer于1983年提出[10]，是对传统功率谱密度的完善补充。Vrabie等[11]首次将谱峭度引入到轴承故障诊断领域中。Antoni于2006年建立了谱峭度理论，引入短时傅里叶变换(short-timeFouriertransform，简称STFT)对谱峭度进行了系统定义，并开发了快速谱峭度算法[12-13]。其基本思想是利用STFT对信号进行处理，对每根谱线上的峭度值进行计算，不仅能够反映冲击特征的强弱，而且能够指出其频带。

在非平稳状态下定义输入X(n)的Wold-Cramer分解的谱形式为

(11)

其中：H(n,f,ω)为频率f处输出Y(n)的复包络，其形状由时变性变量ω决定；dX(f)为输入X(n)的谱过程。

(12)

其中：S2mY(n,f)为X(f)的2m阶瞬时距，表示在时间n、频率f时复包络H(n,f,ω)所含能量的度量。

谱累积量是表征非高斯性最好的统计量。设四阶谱累积量为

(13)

定义输出Y(n)的谱峭度为

(14)

2 实验室数据分析

实验数据来源于美国Case Western Reserve大学轴承数据中心[14]，滚动轴承故障模拟实验台如图1所示。该实验台包括左边的三相感应电机、中间的力矩传感器和联轴节以及右边的测功机。电机驱动端、风扇端以及支撑底座上均安装有加速度传感器。该实验台可测试两种型号的轴承，分别是安装在电机驱动端的SKF6205轴承和安装在风扇端的SKF6203轴承。采用电火花技术模拟工程实际中的点蚀现象，在滚动轴承内、外圈及滚子中加工不同尺寸(直径分别为0.177 8，0.355 6和0.533 4 mm)的故障，将单点故障引入到测试轴承中。

为了验证笔者所提方法的有效性及合理性，同时考虑到轴承外圈缺陷位于6点钟方向承载区时故障特征过于明显，选取点蚀直径为0.177 8 mm(故障程度最小)且位于3点钟位置时的驱动端轴承外圈故障数据进行分析。实验时电机转速为1 797 r/min，采样频率为12 kHz，相应的外圈故障特征频率为107.3 Hz。取采样数据的前5 000个点，处理前原始信号的时域波形和包络谱如图3所示。可以看出，原始信号背景噪声较大，冲击特征不明显，包络谱也无法判别故障类型，因此首先采用MED方法对信号进行背景噪声消除。

图2 滚动轴承故障模拟实验台Fig.2 Test rig for bearing fault detection

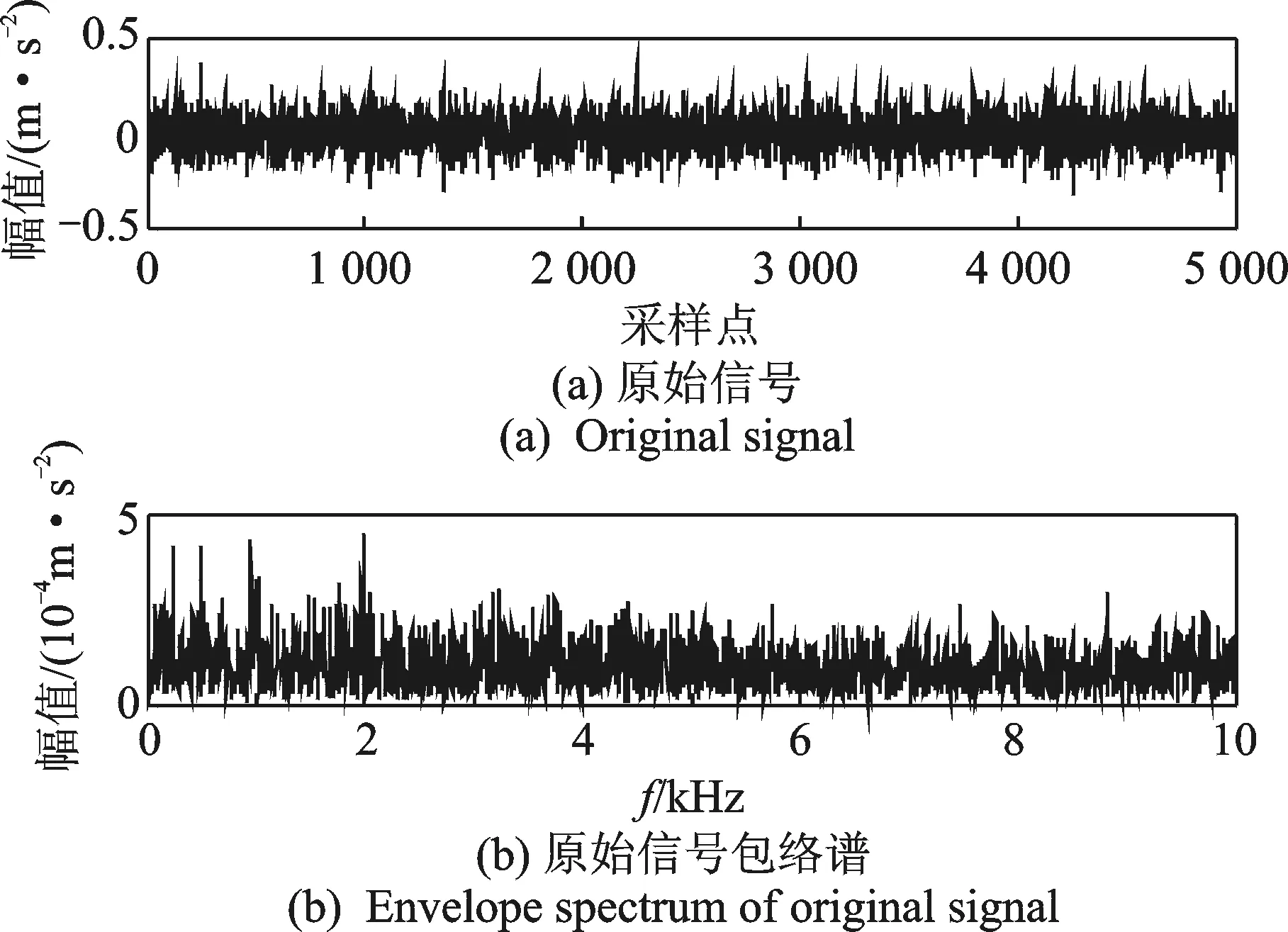
图3 轴承外圈故障信号及其包络谱Fig.3 Signal and its envelope spectrum from outer race fault

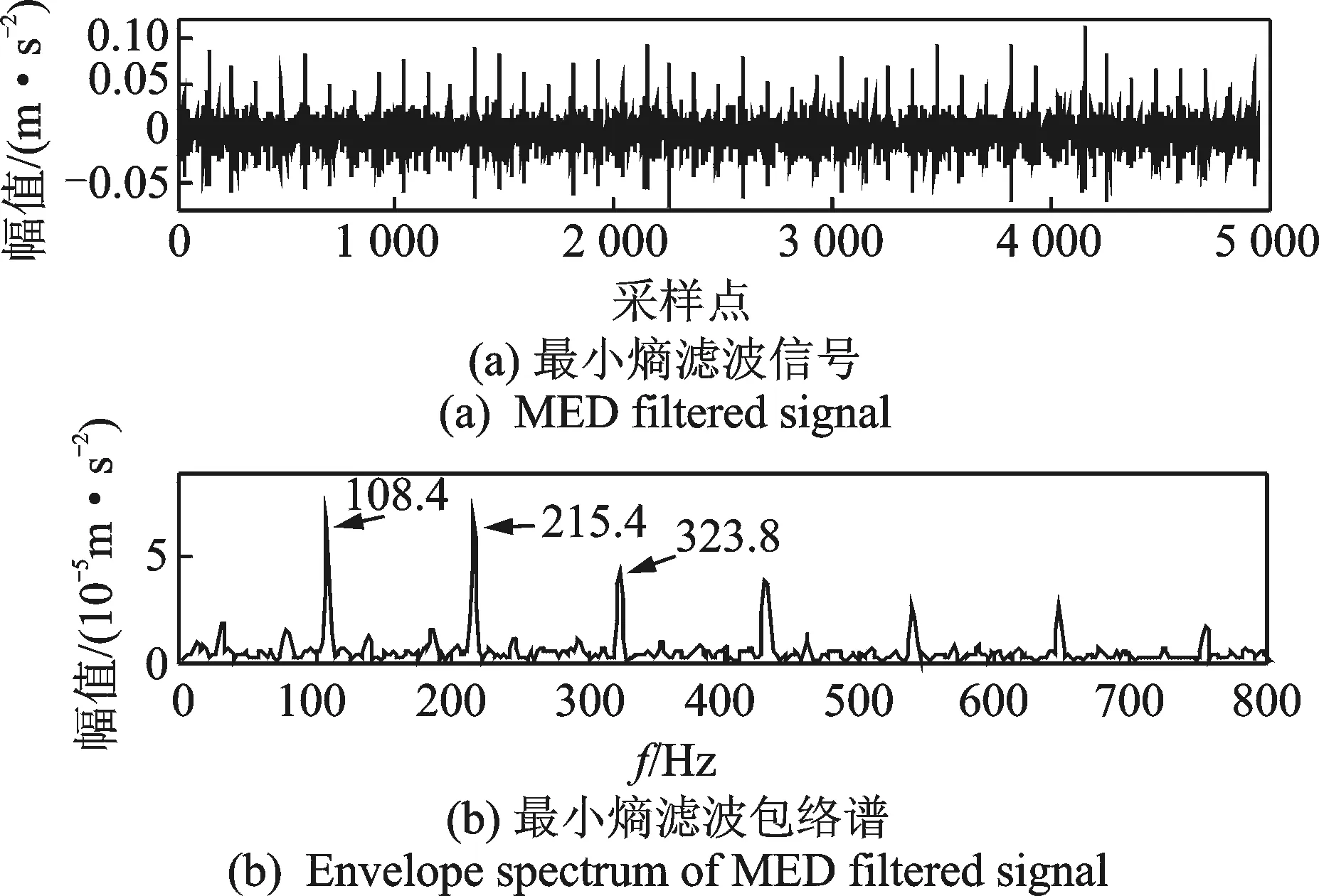
图4 轴承外圈信号的最小熵滤波信号及其包络谱Fig.4 MED filtered signal and its envelope spectrum of a bearing with outter race fault

图4(a)为采用最小熵解卷积法对图3(a)进行消噪后的时域波形。与图3(a)相比，图中原始信号中的脉冲冲击特征得到明显增强，并呈现明显的周期性，部分原始信号中的微弱冲击特征也得到凸显。图4(b)为图4(a) MED消噪信号的包络谱。其中，108.4 Hz频率成分与 BPFO=107.3 Hz 接近，且存在明显的倍频成分，其他频率成分及噪声很小，因此可以判定轴承已有严重外圈故障，无需进行谱峭度二次滤波。

3 工程应用

货车滚动轴承早期故障轨边声学诊断系统(trackside acoustic detection system, 简称TADS)利用安装在钢轨两侧的声学传感器阵列对运行状态下的列车声音信号进行数据采集，通过对声音信号的分析来实现轴承故障检测[15]。图5为某 TADS 探测站检测到的含有内圈故障的铁路货车轴承解体结果示意图。轴承型号为197726TN，检测时车速为38 km/h，信号采样频率为48 kHz，轴承内圈转速为240 r/min，经计算可得内圈故障特征频率为44 Hz。

处理前原始信号的时域波形和包络谱如图6所示。可以看出，原始信号背景噪声大，无法辨别冲击特征位置，包络谱分析也无法根据所给条件判别故障类型。图7(a)为采用最小熵解卷积法对图6(a)处理后的时域波形。因背景噪声太大，滤波效果不佳，轴承故障类型依然无法判别。在此例中，显然仅采用MED方法并不能有效提取轴承故障特征，因此需要利用谱峭度方法对信号进行二次滤波。

图5 铁路货车内圈故障轴承Fig.5 Bearing of railway freight car with inner race fault

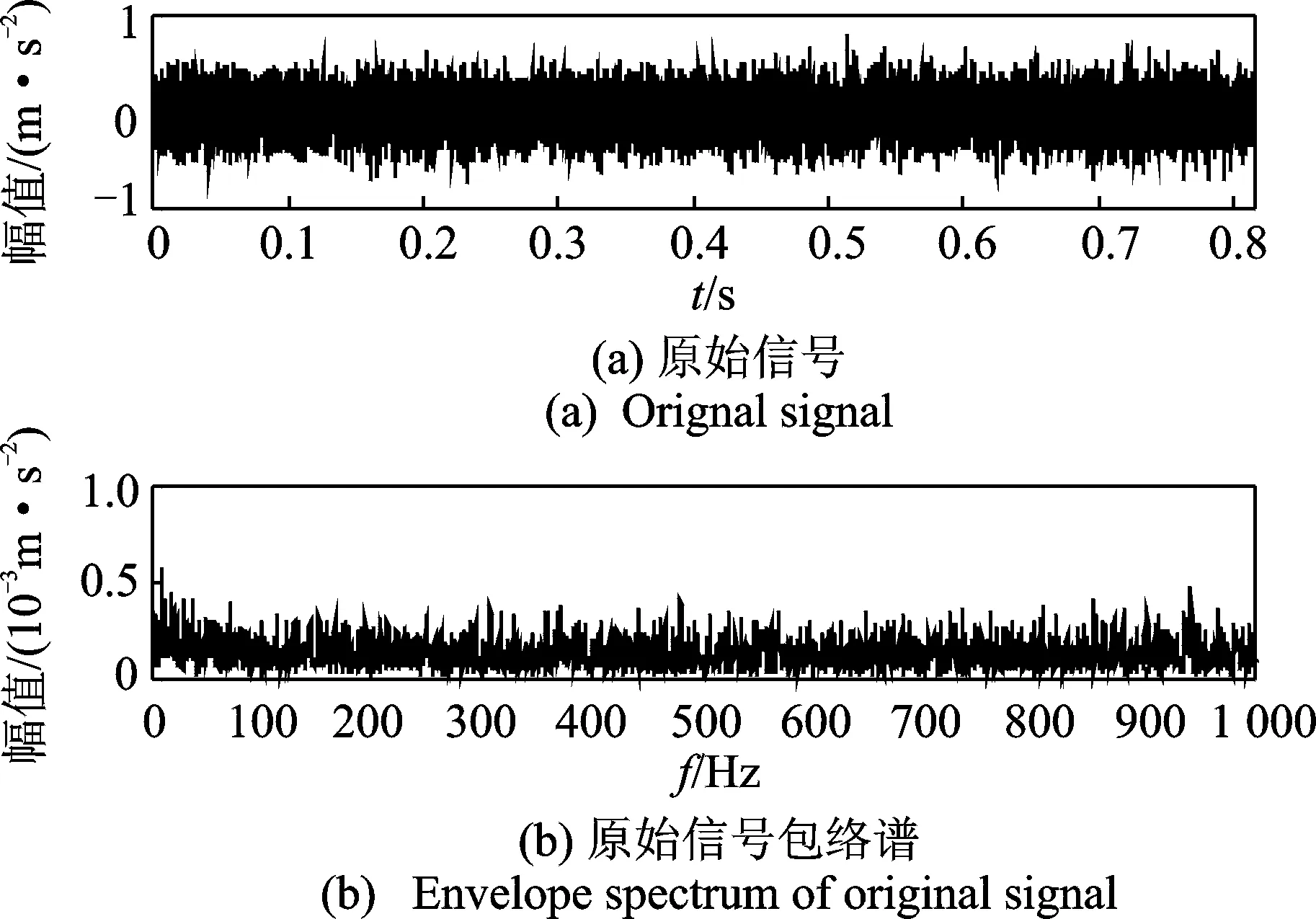
图6 原始声音信号及其包络谱Fig.6 The original sound signal and its envelope spectrum

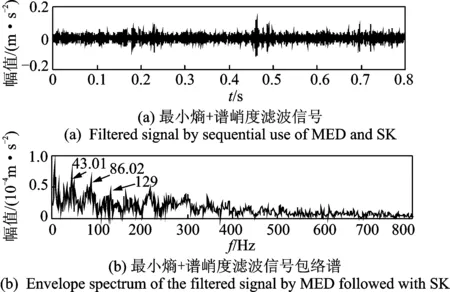
图9 MED和SK联合滤波后的信号及其包络谱Fig.9 The filtered signal and its envelope spectrum by sequential use of MED and SK

图8为MED滤波后所得图7(a)所示信号的谱峭度图。可知最大峭度值为2，处于第6.5层上。相应的最优带通滤波器的中心频率为13 125 Hz，带宽为250 Hz。利用谱峭度法得到的最优带通滤波器对MED滤波信号进行二次滤波，如图9(a)所示。相比图7(a)，背景噪声信号得到明显抑制，轴承故障冲击特征得到了一定程度的增强。图9(b)包络谱上的 43.01 Hz 频率成分与内圈故障特征频率44 Hz接近，且存在两倍频和三倍频成分，可判定轴承存在内圈故障。说明如果MED消噪效果不理想，需要进一步采用谱峭度二次滤波以确定是否存在轴承故障及判断故障类型。

4 结 论

1) 实验室测得的信号由于外界干扰较小，MED消噪足以使信号的尖锐突变得到增强，能够较为准确地找到信号的冲击特征，此时无需进行SK二次滤波。

2) 对于通过声音传感器采集的实际运行列车的轮对轴承声音信号，因为测量噪声和环境干扰较大，仅通过MED无法有效提取故障特征频率。此时利用SK进行二次滤波，消除测量和环境噪声影响，轴承故障特征能够得到明显增强。

[1] 张志刚, 石晓辉, 施全, 等.基于改进EMD和谱峭度法滚动轴承故障特征提取[J]. 振动、测试与诊断, 2013, 33(3): 478-482.

Zhang Zhigang, Shi Xiaohui, Shi Quan,et al. Fault feature extraction of rolling element bearing based on improved EMD and spectral kurtosis [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(3): 478-482.(in Chinese)

[2] 从飞云, 陈进, 董广明. 基于谱峭度和AR模型的滚动轴承故障诊断[J]. 振动、测试与诊断, 2012, 32(4): 538-541.

Cong Feiyun, Chen Jin, Dong Guangming. Spectral kurtosis and AR model based method for fault diagnosis of rolling bearings [J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(4): 538-541.(in Chinese)

[3] 江瑞龙. 基于最小熵解卷积的滚动轴承故障诊断研究[D]. 上海: 上海交通大学, 2013.

[4] Wiggins R A. Minimum entropy deconvolution [J]. Geoexploration, 1978, 9(16): 21-35.

[5] 马涛, 秦轶翚, 魏绍谦. 基于最小熵翻卷积的网络故障特征提取仿真[J]. 计算机仿真, 2015, 32(4): 269-272.

Ma Tao, Qin Yihui, Wei Shaoqian. Simulation on network fault feature extraction based on minimum entropy turn convolution [J]. Computer Simulation, 2015, 32(4): 269-272.(in Chinese)

[6] 梁巍. 管道缺陷检测中超声信号稀疏解卷积及稀疏压缩方法的研究[D]. 上海：上海交通大学, 2008.

[7] 刘志川, 唐力伟, 曹立军, 等. 基于MED-SVM的齿轮箱故障诊断方法[J]. 机械传动, 2014, 38(12): 124-127.

Liu Zhichuan, Tang Liwei, Cao Lijun,et al. Fault diagnosis method of gearbox based on MED-SVM[J]. Journal of Mechanical Transmission, 2014, 38(12): 124-127.(in Chinese)

[8] 姚炽伟, 樊新海, 黄梦. 基于MED的滚动轴承故障特征提取方法及其应用[J]. 装甲兵工程学院学报, 2013, 27(3): 35-38.

Yao Chiwei, Fan Xinhai, Huang Meng. Rolling bearing fault feature extraction method based on MED and its application [J]. Journal of Academy of Armored Force Engineering, 2013, 27(3): 35-38.(in Chinese)

[9] Walden A T. Non-Gaussian reflectivity，entropy and deconvolution [J]. Geophys, 1985, 50(12) : 2862-2888.

[10]Dwyer R F. Detection of non-gaussian signals by frequency domain kurtosis estimation [C]∥Acoustic， Speech and Signal Processing. Boston: IEEE International Conference on ICASSP, 1983, 83: 607-610.

[11]Vrabie V, Granjon P, Maroni C, et al. Application of spectral kurtosis to bearing fault detection in motors [C]∥5thInternational Conference on Acoustical and Vibratory Surveillance Methods and Diagnostic Techniques. France: HAL-CCSd-CNRS, 2004:1-10.

[12]Antoni J, Randall R B. The spectral kurtosis: a useful tool for characterizing non-stationary signals [J].Mechanical Systems and Signal Processing, 2006, 20(2): 282-307.

[13]Antoni J. Fast computation of the Kurtogram for the detection of transient faults [J]. Mechanical Systems and Signal Processing, 2007, 21(1):108-124.

[14]Case Western Reserve University. Bearing data center [EB/OL].2014-01-06.http:∥csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website.

[15]Cline J, Bilodeau J, Smith R. Acoustic wayside identification of freight car roller bearing defects[C]∥ASME/IEEE, Joint Railroad Conference.Piscataway：IEEE, 1998: 79-83.

10.16450/j.cnki.issn.1004-6801.2017.01.015

*国家自然科学基金资助项目(51665013,51265010,51205130)；江西省科协重点活动资助项目(赣科协字[2014]154号)；江西省青年科学基金资助项目(20161BAB216134)

2015-04-08；

2015-06-19

TH133.3

张龙，男，1980年11月生，博士、副教授。主要研究方向为工程信号处理与智能算法及其在机械故障诊断中的应用。曾发表《复小波共振解调频带优化方法和新指标》(《机械工程学报》2015年第51卷第3期)等论文。 E-mail: longzh@ecjtu.edu.cn 通信作者简介：熊国良，男，1962年11月生，博士、教授。主要研究方向为机电设备动态特性分析与监测诊断。 E-mail: lgxcxx@ecjtu.edu.cn