配对样本T检验在赤足迹与穿鞋足迹同一认定中的应用性研究

马晓赟，王 彪

（中国刑事警察学院，辽宁 沈阳110035）

一、引言

2016年10月11日，最高人民法院等五院部联合印发并实施《关于推进以审判为中心的刑事诉讼制度改革的意见》，这一重大改革意味着鉴定人员的任务不仅仅是要为抓捕犯罪嫌疑人提供线索，更要以强有力的证据将其送上法庭。

足迹是案发现场出现率最高的一类痕迹，且提取率也高于其他痕迹物证。〔1〕相对于其他痕迹物证，足迹更不易伪装，它所提供的信息能够更全面地反映嫌疑人的个人信息。多年足迹学的理论研究与实践说明足迹可用于判断嫌疑人的性别、身高、体态、年龄、来去路线，甚至是职业和习惯等，这为刻画嫌疑人特征，划定侦查范围提供了重要依据。近年来，由于各种主客观原因的制约，足迹检验越来越倾向于提出种属性检验意见，为侦查提供线索，而极少形成同一认定的鉴定报告。诉讼制度的改革促使足迹检验人员需确定嫌疑人足能否形成现场足迹，使检验鉴定意见成为呈堂证供，变得尤为关键。

现场遗留的足迹大多为嫌疑人的穿鞋足迹，基本的足迹分析方法是直接收集嫌疑人的案后样本（足-鞋1-地）与检材痕迹（足-鞋1-地）比较检验，此方法固然好却有其局限性。因为嫌疑人很可能在作案后丢弃或销毁作案鞋，使其无法找回，导致不能进行同人同鞋的检验鉴定。若使用传统方法将嫌疑人的案后样本（足-鞋2-地）与检材痕迹（足-鞋1-地）比较，则易受到不同鞋材质、样式、大小、新旧的影响，结果误差较大，使得检验鉴定陷入困境。此时，如收集嫌疑人的赤足迹样本（足-地）与检材痕迹（足-鞋1-地）比较，理论上可以大大减少分析误差。配对样本T检验作为统计学中参数检验的重要方法，其能否在足迹检验鉴定中加以利用？本文就尝试提取赤足迹与穿鞋足迹的对应特征参数，利用配对样本T检验进行赤足与穿鞋足的同一认定。

二、理论依据

（一）假设检验假设检验也叫“显著

性检验”，是统计学中的一种重要检验方法。假设检验由一系列假设条件通过样本推断总体特征。具体做法是：首先对待分析总体做出某种合理的假设，再通过样本抽样调查，分析推断是肯定还是否定之前的假设。假设检验根据总体分布是否已知，可以分为参数检验与非参数检验。〔2〕

在总体分布已知（如正态分布）的情况下，对总体包括的参数进行推断的问题称为参数检验。当总体分布未知时，通常采用非参数检验。

（二）配对样本T检验

配对样本T检验是统计学中参数检验的一种有效途径，可以用来检验两组具有相关性的样本数据是否源自同均值的正态分布总体，即推断两个相关的样本总体其均值有无显著差异。其原假设为H0：μ1-μ2＝0，其中，μ1和 μ2分别为第一个总体和第二个总体的均值。配对是指两组样本数据中的各样本值之间一一对应，有对应关系，且两组样本容量相同。所谓配对样本，可以是物质某属性的“前”“后”两种状态，也可以是对某事物两个不同侧面或方面的描述，总之这两种属性或方面必然存在内在的联系。

1.配对样本T检验的数学思想

配对样本T检验是通过求出每组样本对应值之差，从而将各对应样本观测值之差构成一个新的单样本，如果两个样本均值不存在显著差异，则样本值差的均值应近似为零，通过这种方法将对两个待分析总体的检验变换成一个单样本T检验。所以，配对样本T检验就是检验差值所来自的总体其均值是否为零。〔3〕这就要求差值来自的总体服从正态分布。

2.配对样本T检验的检验统计量

在配对样本 T检验中，设 x1i，x2i（i＝1，…，n）分别为配对样本。其样本差值di＝x1i-x2i，此时检验统计量：

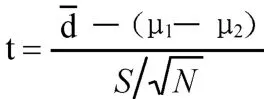
式中，d为di的均值；S为di的标准差；N为样本数。当 μ1-μ2＝0时，t统计量服从自由度为N-1的T分布。

可以在统计分析软件SPSS中计算出两组样本的差值，并将相应数据代入上式的T检验统计量计算公式中，计算T统计量的观测值和对应的概率P值。

三、实验研究

（一）受试对象

分别收集中国刑事警察学院校内20—50岁之间200名师生的赤足迹样本和穿鞋足迹样本。其中男性100名，女性100名。所有受试者无任何足部疾病或下肢损伤。

（二）实验方法

1.样本收集

所有受试者分别以正常步速、正常姿态分别进行赤足迹捺印和穿鞋足迹捺印（实验用鞋要求为受试者长期穿用后的）。将所有样本贴上标签统一编号。

2.标记特征

（1）赤足迹特征分级与量化

赤足迹结构特征包括足型特征、肤纹特征以及其他特征。〔4〕由于本次检验需要选择赤足迹与穿鞋足迹可以一一对应的特征，故不是所有的赤足迹特征都能被选取和使用。人在行走或站立过程中，足与地面相互作用，不同区域的足底压力分布各不相同，在赤足迹捺印样本中反映明显，故按压力大小不同进行足底分区，并选择其中4个重压区域，分别标记为：AX1、AX2、AX3、AX4。AX1为拇趾重压区，AX2为第一跖骨关节重压区，AX3为第五跖骨关节重压区，AX4为足跟中心重压区。再根据压力的轻重程度对四个重点区分级进行量化，由轻至重分别为 1、2、3、4四个等级。〔5〕级别 1为压印较轻，纹线呈浅灰色，在捺印纸张上只有轻微反映；级别2为压印略重，纹线呈灰黑色，极少区域有挤墨显现；级别3为压印重，纹线呈亮黑色，挤墨范围增加；级别4为压印极重，墨迹堆积已无法识别纹线。

再标画各重压区的范围。由于足的解剖结构特点，重压区通常为类圆形区域，以类圆的最长直径与最短直径的交点作为该重压区的中心点，选取测量中心点之间的四段距离标记为：AY1、AY2、AY3、AY4。其中，拇趾重压中心到第一跖骨关节重压中心的距离记为AY1；拇趾重压中心到第五跖骨关节重压中心的距离记为AY2；拇趾重压中心到足跟重压中心的距离记为AY3；第一跖骨关节重压中心到第五跖骨关节重压中心的距离记为AY4。

（2）穿鞋足迹特征的分级与量化

由于鞋具备造痕体与承痕体的双重性质，穿鞋足迹不仅能反映出足底压力的分布，亦以鞋底磨损特征加强这种压力分布的反映性。依据赤足与穿鞋足迹压力特征一一对应，穿鞋足迹特征的分级与量化实际上与赤足迹特征的分级量化类同，只是将足底压力轻重反映为鞋底磨损轻重，将压力中心反映为磨损中心，故在此不再赘述。设定四个对应磨损区域分别为 BX1、BX2、BX3、BX4并分级；设定中心点之间的四段对应距离标记为：BY1、BY2、BY3、BY4。

根据已知研究，左右足双侧的压力分布具有一致性，因此只选用受试者的左足数据〔6〕，如图1所示。

图1 赤足迹与穿鞋足迹对应特征的分级与量化

3.建立数据库

共收集到总计400份实验样本，按赤足迹与穿鞋足迹分类，分别对选取的赤足迹与穿鞋足迹对应的特征参数录入、统计。

四、结果

（一）数据分析

对400份平面赤足迹和穿鞋足迹样本进行统计，得到表1的统计结果（由于样本数据量庞大，且文章篇幅有限，故在此只列举前20对样本数据）。

表1 样本赤足迹与穿鞋足迹对应特征统计表

（二）T检验鉴定

1.描述性分析

配对样本T检验属于参数检验的一类，而参数检验需要满足已知总体分布为正态分布的前提。故首先对统计样本进行描述性统计分析——探索性分析，检验各参数是否满足正态分布。根据已知的足迹学知识，足迹特征受环境、时间、心理、体态等主客观因素影响较多，导致本次实验的随机误差增加，所以将显著性选择为P＜0.05。利用SPSS（Statistical Program for Social Science）19.0统计分析软件检验正态性（由于数据庞大且分析过程较复杂，故本文略去分析过程）得到表2。分析结果，赤足迹与穿鞋足迹样本的各特征参数Sig.值均大于0.05，可知样本总体均满足正态分布，满足配对样本T检验的条件。

表2 赤足迹与穿鞋足迹样本各特征参数正态检验

穿鞋足迹样本特征参数正态性检验

2.配对样本T检验

首先设定原假设为：同一样本的赤足迹与穿鞋足迹标记特征参数无明显差异（可进行同一认定）。则备择假设为：同一样本的赤足迹与穿鞋足迹标记特征参数明显不同。利用SPSS进行配对样本T检验（由于数据庞大且分析过程较复杂，省略分析步骤）。

表3是成对样本的基本描述统计量，从两对样本的均值变化可以看出，均值都有一定量的变化，但要想确定变化是否显著，是否为本质差异，还必须要计算两组样本对应的t统计量。

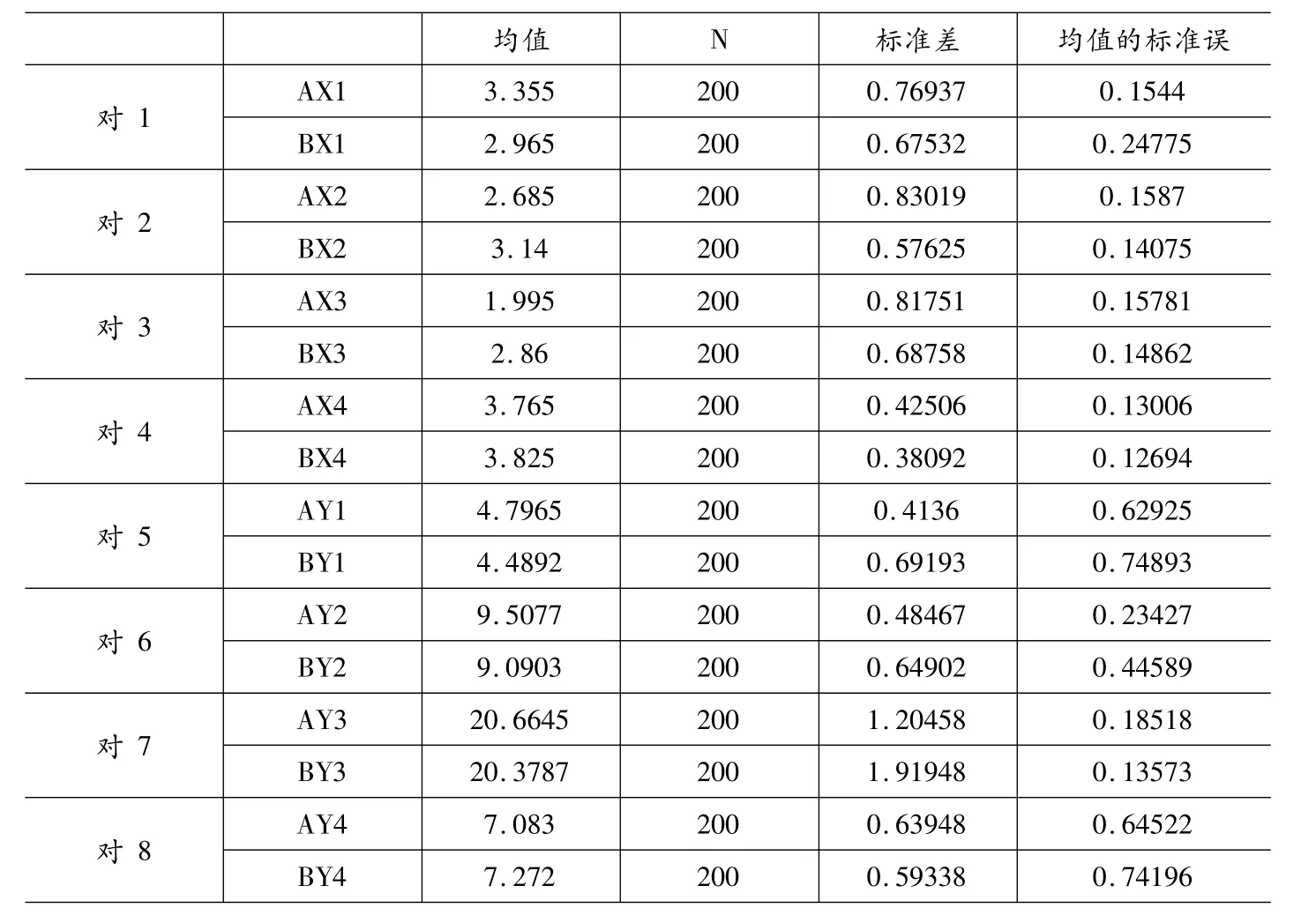
表3 配对样本T检验的基本描述统计量

表4是配对样本T检验的简单相关关系检验结果。表中第3列为赤足迹与穿鞋足迹对应样本参数的相关系数，第4列是相关系数的检验P值。从表中可以看出，在显著性水平为0.05时，概率P值均大于0.05，故接受原假设，可以认为同一样本的赤足迹与穿鞋足迹标记特征参数无明显差异（可进行同一认定）。

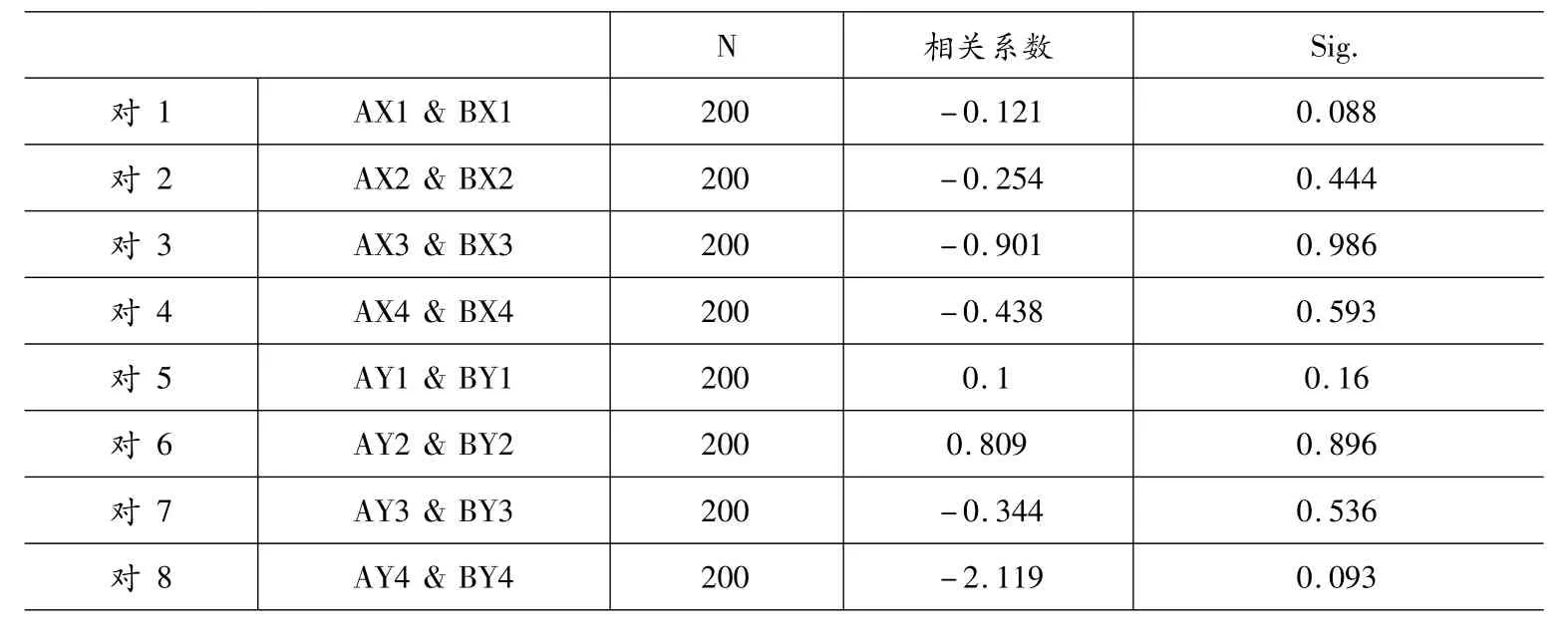
表4 配对样本相关性检验

表5是配对样本T检验的最终结果。置信度为95%，自由度为199，Sig.（双侧）为双尾检验概率P值，在显著性水平为0.05时，由于概率P值均大于0.05，故更加强烈地支持原假设，认为μ1-μ2＝0，更加强烈说明同一样本的赤足迹与穿鞋足迹标记特征参数无明显差异（可进行同一认定），其法庭证据力度增强。

表5 配对样本T检验结果

（三）案例应用

上述配对样本T检验的整个过程，下面以案件实例具体说明。2016年7月15日，在陕西省西安市长安区某小区发生一起盗窃案件，案件现场勘察提取到嫌疑人在纸张上遗留的检材穿鞋足迹a，该枚足迹为穿着皮鞋的左脚足迹。案后收集到1号嫌疑人样本赤足迹两份（b为其一），2号嫌疑人样本赤足迹两份（c为其一），如图2所示：需要鉴定a与b组系同一足所留亦或a与c组系同一足所留。

图2 a为检材足迹，b、c为不同嫌疑人的样本足迹

将a与b，a与c分别按上述方法进行特征分级、量化，并将测量结果统计汇总，在SPSS中录入数据，分两次进行配对样本T检验。第一次原假设设定为a与b系同一样本的赤足迹与穿鞋足迹，可认定同一。表6是a与b进行配对样本T检验的最终结果，在显著性水平为0.05时，由于概率P值均大于0.05，故支持原假设，认为μ1-μ2＝0，满足相似性，a与b系同一样本的赤足迹与穿鞋足迹，可认定同一。第二次原假设设定为a与c系同一样本的赤足迹与穿鞋足迹，可认定同一。表7是a与c进行配对样本T检验的最终结果，在显著性水平为0.05时，由于概率P值不全大于0.05，故否定原假设，认为μ1-μ2≠0，满足典型性，a与c非同一样本的赤足迹与穿鞋足迹，可否定同一。

综合评断，a与b系同一足所留赤足迹与穿鞋足迹，可认定同一，证实1号嫌疑人为真凶。由此证明，配对样本T检验模型在公安实际应用领域的可行性。

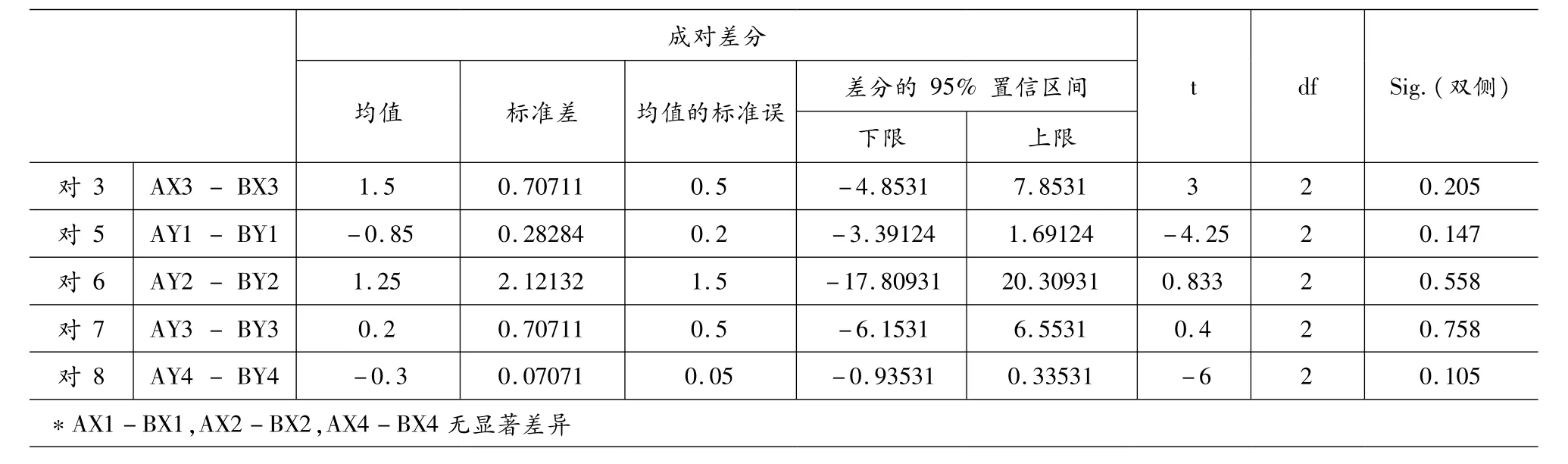
表6 配对样本T检验结果（a-b）

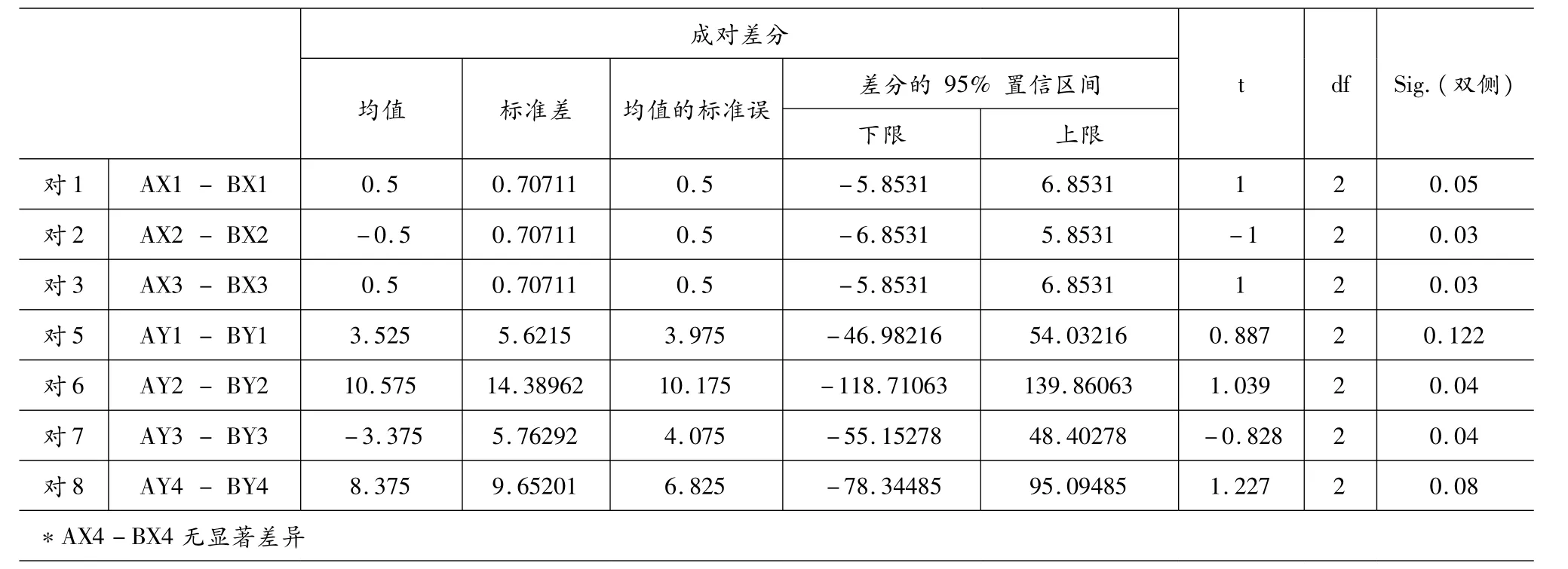
表7 配对样本T检验结果（a-c）

五、结论

本文针对利用配对样本T检验对赤足迹与穿鞋足迹同一认定进行了研究尝试，结果证明该方法在足迹检验领域是可行的。但还有诸多待完善之处，例如选取样本特征较少、人为操作误差较大等，下一步将完善实验数据，结合足迹的步幅特征、步态特征，以及其他关联物证，对赤足与穿鞋足的同一认定做进一步系统量化检验。