一维非定常对流扩散反应方程的高精度紧致差分格式

杨晓佳，田芳

(宁夏大学 数学统计学院,宁夏 银川 750021)



一维非定常对流扩散反应方程的高精度紧致差分格式

杨晓佳，田芳

(宁夏大学 数学统计学院,宁夏 银川 750021)

针对一维非定常对流扩散反应方程，首先推导了一种新的2层高精度紧致差分隐格式，其截断误差为O(τ2+τh2+h4)，即当τ=O(h2)时，格式空间具有四阶精度；然后采用Fourier分析方法分析了格式的稳定性；最后通过数值算例验证了本文格式的精确性和可靠性.

对流扩散反应方程；非定常；紧致差分格式；隐式格式；高精度

MSC 2010：O 241.82

对流扩散反应方程是描述黏性流体流动的非线性方程的线性化模型方程，该方程可用于描述许多自然现象，例如水和大气中污染物质浓度的扩散，海水盐度﹑温度的扩散，流体流动和流体传热等过程，因此寻求此类方程稳定、实用的数值方法有着重要的理论与实际意义.目前大多数的文献报道都针对的是对流扩散方程模型，如葛永斌[1]等人通过时间导数项采用二阶的向后欧拉差分公式，空间二阶导数采用四阶紧致差分公式，最终得到了一种求解含源项非定常变系数对流扩散方程的3层四阶紧致隐格式；Ding和Zhang[2]针对一维对流扩散方程，采用半离散的方法和Padé逼近法，推导了一种截断误差为O(τ5+h4)的无条件稳定的 隐格式.Tian和Yu[3]采用四阶紧致指数差分公式和(2,2)Padé公式分别对空间变量和时间变量进行离散，推导了一种求解一维非定常对流扩散方程的四阶精度的无条件稳定的紧致差分隐格式；赵飞[4]等人针对一维非定常对流扩散方程，考虑方程在n+1/2时刻的值，时间上利用中心差分格式，空间上采用截断误差余项修正的方法及加权平均的思想，最终推导出了非均匀网格上的一种2层高精度全隐式紧致差分格式；Piao等[5]针对一维非定常对流扩散方程，采用3点紧致差分格式和快速单对角隐式Runge-Kutta方法分别对空间和时间进行离散，得到了截断误差为O(τ4+h4)的无条件稳定的隐格式.也有一些科研工作者针对对流扩散反应方程模型展开研究，如Wo等[6]针对一维非定常对流扩散反应方程，采用Godunov方法，推导出了一种高精度的显式差分格式.魏剑英[7]提出了一种求解非定常对流扩散反应方程的无条件稳定的隐式差分格式，此格式的时间和空间方向均具有二阶精度.Liao[8]先将一维非定常对流扩散方程转化为扩散方程，然后采用四阶紧致差分格式，最终推导出了一种截断误差为O(τ4+h4)的无条件稳定的隐格式，该论文利用此格式计算了对流扩散反应问题.赵秉新[9]针对一维对流扩散反应方程，通过指数变换将原方程变换为对流扩散方程，对变换后的方程中的对流项和扩散项分别采用高阶迎风紧致差分格式和对称紧致格式进行离散，在时间上采用四阶Runge-Kutta方法进行推进，从而得到一种截断误差为O(τ4+h4)的紧致差分格式.杨录峰等[10]针对对流扩散反应方程，采用消除对流项的处理技巧，结合四阶Padé公式推导出了一种无条件稳定的高精度差分格式.

本文针对一维非定常变系数对流扩散反应方程，首先采用泰勒级数展开法和余项修正法，得到一种高精度紧致隐格式.然后采用Fourier分析法分析了格式的稳定性.最后通过数值实验对本文方法的精确性和可靠性进行验证.

1 高阶紧致差分格式的建立

考虑如下一维变系数非定常对流扩散反应方程

(1)

其中，a为正常数，p(x,t)为对流项系数，q(x,t)为反应项系数，f(x,t)为源项.以τ表示时间步长，空间取等间距网格，步长用h表示.网格点为(xi,tn)，xi=ih,tn=nτ，i=0，1，…,N,n≥0.

考虑方程(1)在n第时刻的值并对时间和空间导数项分别采用向前和中心差分离散可得

(2)

).

(3)

为了得到时间二阶和空间四阶精度的紧致差分格式，需对式(3)中的时间二阶导数项、空间三阶和四阶导数项进行处理，为此对原方程(1)两边关于和分别求导并整理得

(4)

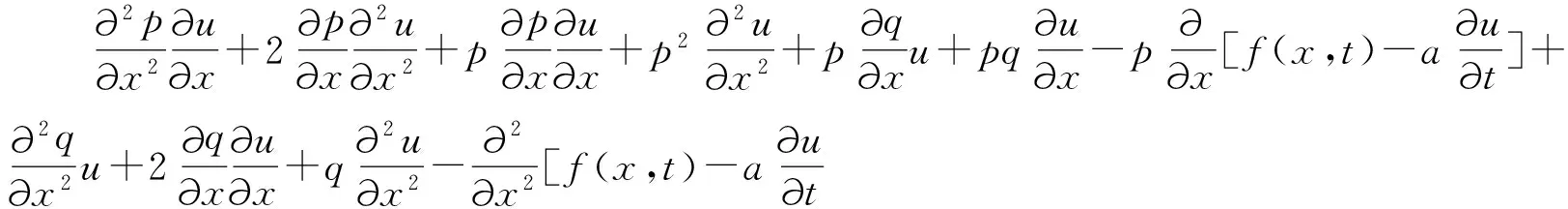
(5)

(6)

在式(4)、(5)和(6)中，全部变量关于空间的一阶和二阶导数项采用中心差分公式离散，未知量关于时间的一阶导数项采用向前差分公式离散，各项系数p,q及右端项f关于时间的一阶导数项采用二阶向后欧拉差分公式离散，并整理得

(7)

(8)

(9)

(10)

将式(7)、(8)和(9)代入式(3)中并整理，可得到方程(1)的高阶紧致差分格式

(11)

其中，

(12)

由推导过程可知，差分格式(11)的截断误差为O(τ2+τh2+h4)，即当τ=h2时，格式在空间具有四阶精度.注意到差分格式(11)对未知量u只涉及到了2层，但是对各项系数p,q和右端源项f涉及到了3层，由于这些函数都是已知的，因此可直接计算，不需要另外构造格式启动.

2 稳定性分析

下面对格式(11)的稳定性进行分析.

考虑齐次的非定常对流扩散反应方程，即令方程(1)式右端项f=0，变形整理可得

(13)

取p(x,t)/a的上确界为Q，q(x,t)/a的上确界为C，令K=1/a，则(13)式变为

(14)

根据格式式(11)的推导过程，可得式(14)的离散格式为

(15)

其中，

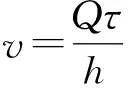
(16)

(17)

则

(18)

其中，

A=(wi-1+wi+1)cosr+wi,B=(wi-1-wi+1)sinr,

F1=(gi-1+gi+1)cosr+gi,F2=(gi-1-gi+1)sinr.

在r-v平面内作出|G|的等值线，图1-4中分别给出了Pe=1、10、100、1 000，均取R=1时，|G|的等值线，|G|<1的区域表示格式稳定，|G|>1的区域表示格式不稳定.从图中可以看出，差分格式式(11)对小波数以及大部分中小波数是稳定的，图3和图4表明，随着Pe数的增加，差分格式式(11)的稳定区域不再发生变化.

3 数值算例

为了验证本文方法的精确性和可靠性，下面选取以下4个算例进行数值实验，算例中的右端项f(x,t)及初边值条件均由精确解给出， 并与已有文献计算结果进行比较.计算是用Fortran 77语言进行编程，且在PC机上双精度制下进行的，离散后在每一个时间层上所得到的代数方程组可采用追赶法进行求解.

图1 当R=1,Pe=1时，在r-v平面内|G| 的等值线

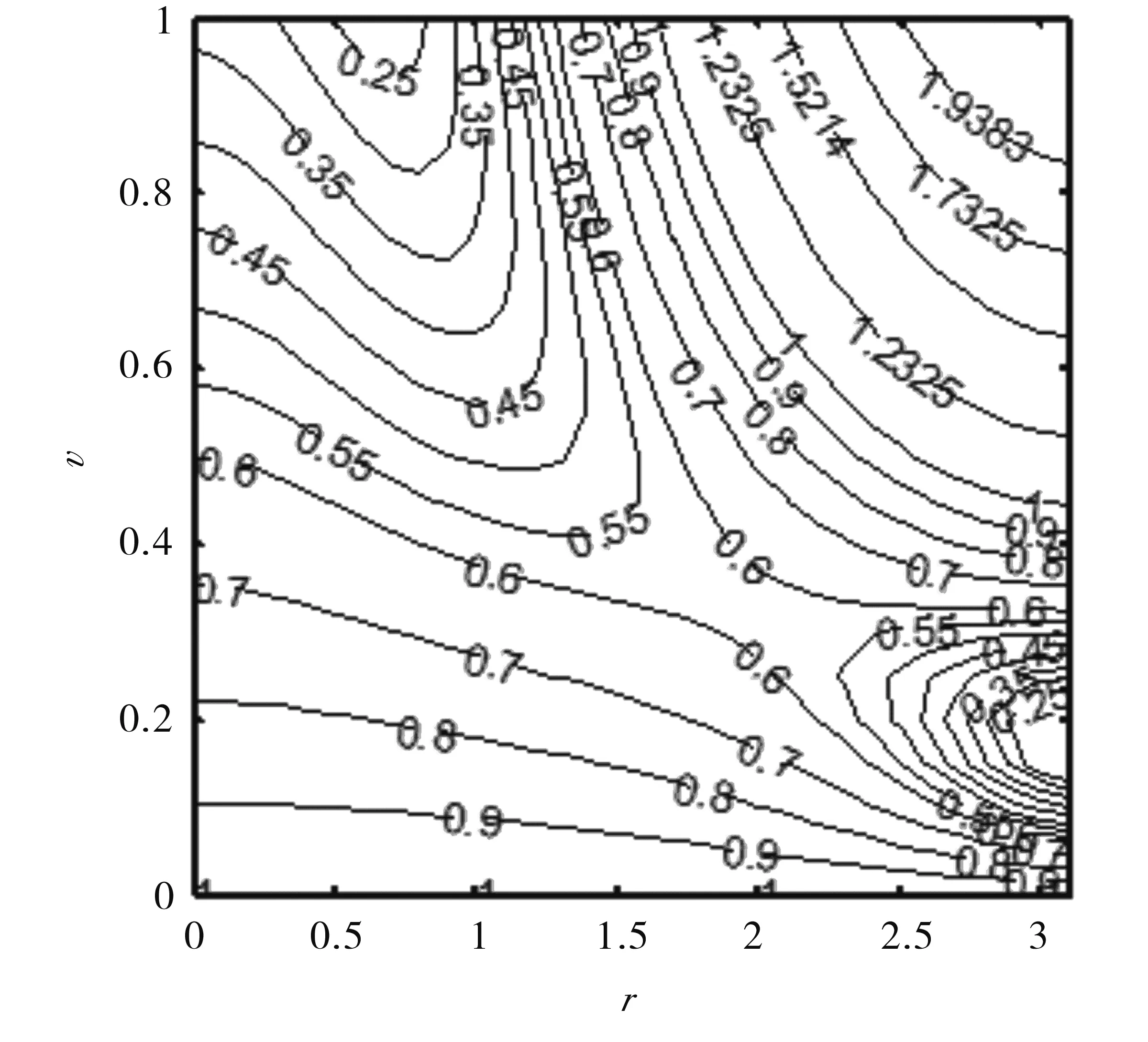
图2 当R=1,Pe=10时，在r-v平面内|G| 的等值线

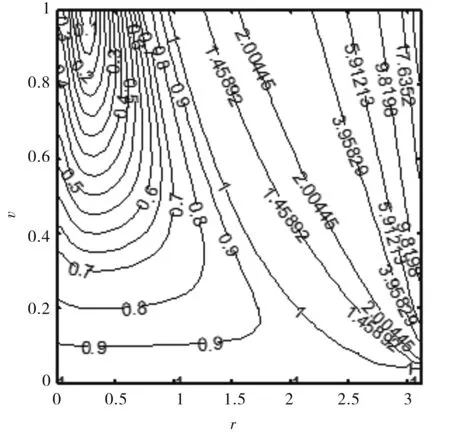
图3 当R=1,Pe=100时，在r-v平面内|G| 的等值线

图4 当R=1,Pe=1 000时，在r-v平面内|G| 的等值线 Fig.4 Contours of the amplification factor |G| in the r-v plane for R=1,Pe=100

其中Ui表示点xi处的精确解，ui表示点xi处的数值解，Error(N1)和Error(N2)分别表示网格数为N1和N2时对应的最大绝对误差.

算例1[1]

其精确解为u(x,t)=e-tsin(x).

表1 问题1当τ=h2,t=0.5时的最大绝对误差及收敛阶

算例2[2,9]

其精确解为u(x,t)=e-tsin(x).

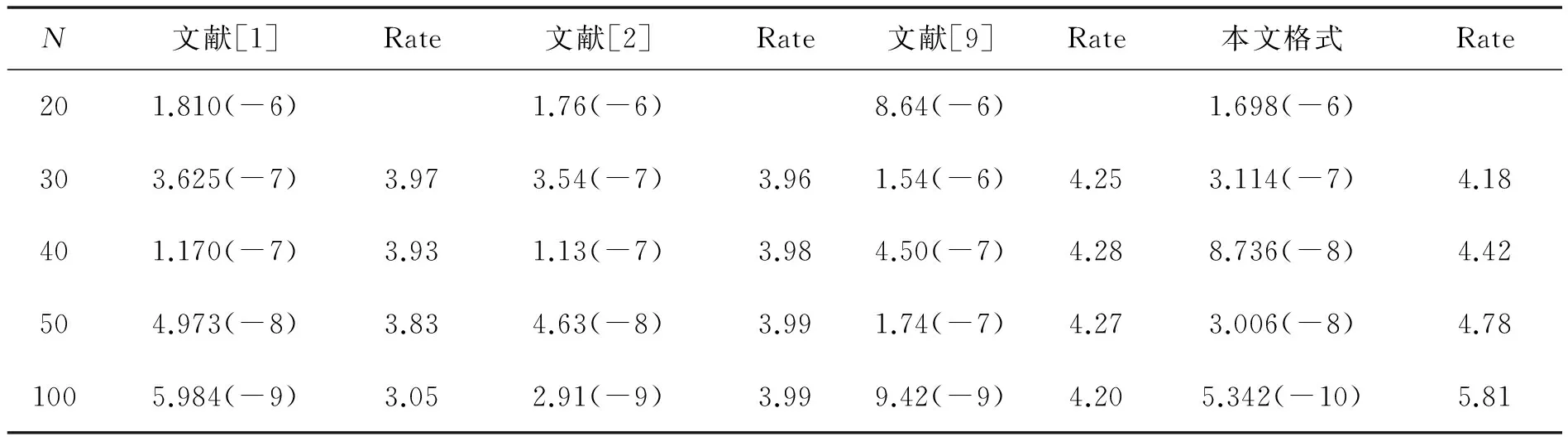
表2 问题2当τ=0.001,t=20时的L2误差及收敛阶

算例3

其精确解为u(x,t)=e5x+t(0.25+0.1π2)sinπx.

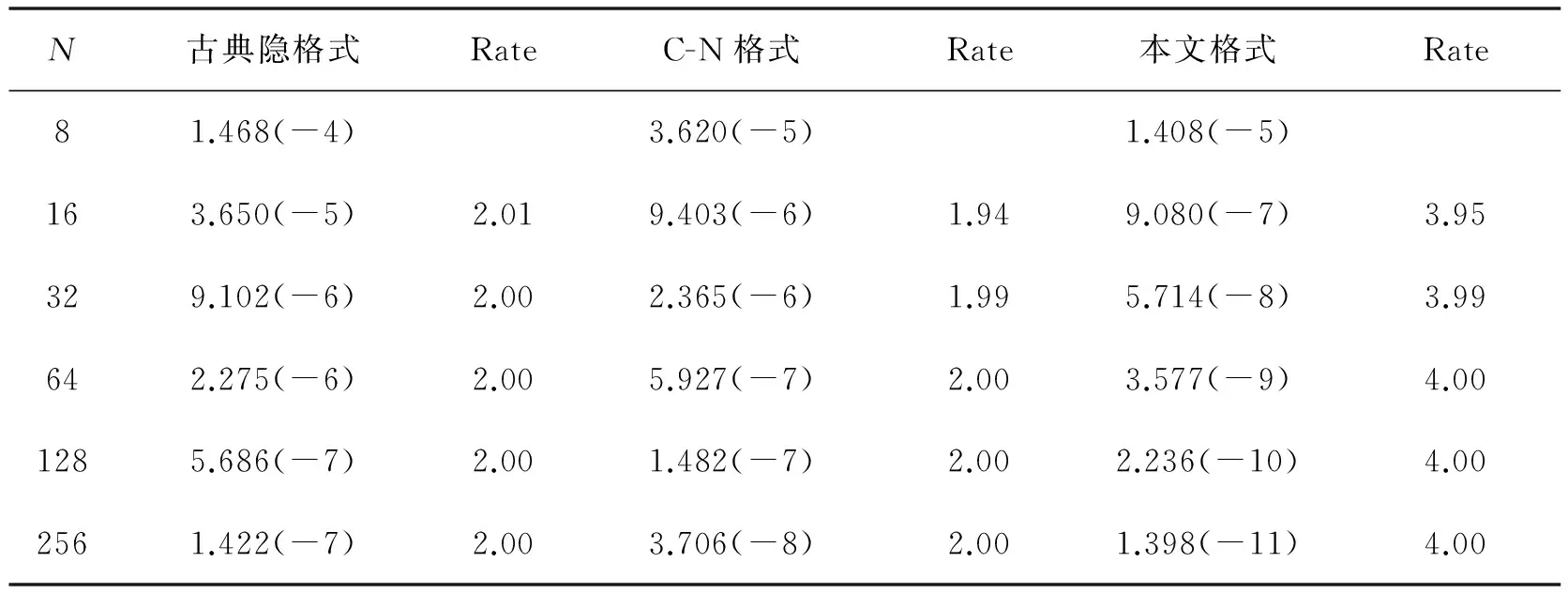
表3 问题3当τ=h2,t=0.5时的最大绝对误差及收敛阶

表4 问题3当N=32,t=1时对不同的网格比的最大绝对误差

算例4

表5 问题4当τ=h2,t=1时的最大绝对误差及收敛阶

算例1是对流扩散方程，表1给出了算例1当τ=h2,t=0.5时的最大绝对误差和收敛阶的比较.从表中的计算结果可以看出，古典隐格式和C-N格式空间只具有二阶精度，本文格式(11)空间具有四阶精度，这与格式的理论分析相吻合.文献[1]对此问题空间也具有四阶精度，但本文格式的计算结果比文献[1]的计算结果更加精确，并且文献[1]中的格式为3层格式，需要另外构造格式来启动，而本文格式为2层格式，在计算过程中不需要另外构造格式来启动，这使得本文格式使用时更加简便.算例2是对流扩散方程，表2给出了算例2当τ=0.001,t=20时的L2误差和收敛阶的比较.从表中的计算结果可以看出，本文格式与文献[1,2,9]中的格式空间均具有四阶精度，但文献[1]中的格式是一个3层格式，需要另外构造格式来启动，文献[2]中的格式在求解过程中需要进行矩阵求逆和乘积等运算，当网格数很大时，这2种格式的求解效率会明显下降，本文格式的L2误差比文献[1,2,9]中格式的L2误差小，这说明本文格式具有更高的计算精度.算例3是一个对流扩散反应方程，由于文献[1,2]中未给出关于此类方程的计算格式，所以在此处未与文献[1,2]做比较而仅与古典隐格式和C-N格式进行了比较.表3和表4分别给出了算例3的计算结果，其中表3给出了当τ=h2,t=0.5时，算例3的最大绝对误差和收敛阶的比较.从表中的计算结果可以看出，本文格式(11)对此问题空间仍具有四阶精度，而古典隐格式和C-N格式空间只具有二阶精度，并且本文格式的最大绝对误差比古典隐格式小1～4个数量级，比C-N格式小1～3个数量级.表4给出了当t=1时，网格数N取32，网格比λ分别取0.4,0.8,1.6,3.2,6.4时，算例3的最大绝对误差，表中的计算结果与稳定性的理论分析是一致的.算例4也是一个对流扩散反应问题，表5给出了当τ=h2,t=1时，算例4的最大绝对误差和收敛阶的比较.从表中的计算结果可以看出，本文格式对此问题空间具有四阶精度，而古典隐格式和C-N格式对此问题的空间只具有二阶精度，并且本文格式的最大绝对误差比古典隐格式小2～4个数量级，比C-N格式小1～4个数量级，当网格数较少时，古典隐格式和C-N格式的最大绝对误差较大.

4 结论

首先建立了一种数值求解一维非定常对流扩散反应方程的2层全隐式紧致差分格式，格式在每个时间层上只用到了3个网格点，所以差分离散得到的代数方程组是三对角方程组，故可采用追赶法进行求解.然后，通过Fourier分析方法分析了格式的稳定性.最后选取了4个典型数值算例进行了数值实验.数值实验结果表明，当τ=O(h2)时，本文格式在空间上可以达到4阶精度，与文献中的计算结果的比较显示，本文方法总体上具有更高的计算精度.

此外，本文虽然只给出了一维对流扩散反应方程的高精度紧致隐格式，但此方法可以推广到高维问题的求解.对于高维方程的隐格式的求解，所得到的方程组不再是三对角线型的，所以不能直接采用追赶法，一般需要迭代求解.然而传统的迭代法收敛速度很慢，为此可采用多重网格方法来加速收敛.文献[11,12]给出了高维对流扩散方程的高精度隐式差分格式及其多重网格算法，取得了较好的计算效果.从理论上讲，将本文方法推广到高维的对流扩散反应方程后，同样可以采用多重网格方法进行加速求解.

[1] 葛永斌,田振夫,吴文权.含源项非定常对流扩散方程的高精度紧致隐式差分方法[J].A辑,水动力研究与进展,2006,21(5):619-625. GE Y B,TIAN Z F,WU W Q.A high-order compact implic it difference method for the unsteady convection-diffusion equation with source term[J].Journal of Hydrodynamics,2006,21 (5):619-625.DOI:10.3969/j.issn.1000-4874.2006.05.010.

[2] DING H,ZHANG Y.A new difference scheme with high accuracy and absolute stability for solving convection-diffusion equatons[J].Comput Appl Math,2009,230:600-606.DOI.org/10.1016/j.cam.2008.12.015.

[3] TIAN Z F,YU P X.A high-order exponential scheme for solving 1D unsteady convection-diffusion Equations[J].J Comput Appl Math,2011,235:2477-2491.DOI.org/10.1016/j.cam.2010.11.001.

[4] 赵飞,陈建华,葛永斌.一维非定常对流扩散方程非均匀网格上的高阶紧致差分格式[J].西安理工大学学报,2013,29 (4):475-480. ZHAO F,CHEN J H,GE Y B.A High order compact difference scheme on non-uniform grids for the 1D unsteady convection diffusion equation[J].Journal of Xi`an University of Technology,2013,29 (4):475-480.

[5] PIAO X,CHOI H J,KIM S D,et al.A fast singly diagonally implicit Runge-Kutta method for solving 1D unsteady convection-diffusion equations[J].Numer Methods Partial Differential Eq,2013,30:788-812.DOI.org/10.1002/num.21832.

[6] WO S,CHEN B M,WANG J.A high-order Godunov method for one-dimensional convection-diffusion-reaction problems[J].Numer Methods Partial Differential Eq,2000,16:495-512.DOI.org/10.1002/1098-2426(200011)16:6<495:aid-num1>3.0.co;2-s.

[7] 魏剑英.求解对流扩散反应方程的一种隐式差分格式[J].四川理工学院学报(自然科学版),2011,24(5):580-582. WEI J Y.An implicit scheme of the 1D convection-diffusion-reaction equation[J].Journal of Sichuan University of Science & Engineering(Natural Science Edition),2011,24(5):580-582.

[8] LIAO W.A compact high-order finite difference method for unsteady convection-diffusion equation[J].Intern J Comput Meth Eng Sci Mech,2012,13:135-145.DOI.org/10.1080/15502287.2012.660227.

[9] 赵秉新.一种求解一维对流扩散反应方程的高阶紧致格式[J].重庆理工大学学报(自然科学版),2012,26(7),100-104. ZHAO B X.A High-order compact difference scheme for solving 1D convection-diffusion-reaction equation[J].Journal of Chongqin University of Technology(Natural Science),2012,26(7),100-104.

[10] 杨录峰,李春光.一种求解对流扩散反应方程的高精度紧致差分格式[J].宁夏大学学报(自然科学版),2013,34(2):101-109. YANG L F,LI C G.A High-order compact finite difference scheme for solving the convection diffusion reaction equations[J].Journal of Ningxia University(Natural Science Edition),2013,34(2):101-109

[11] 葛永斌,吴文权,田振夫.二维对流扩散方程的高精度全隐式多重网格方法[ J ].计算力学学报,2004,21 (6):678-682. GE Y B,WU W Q,TIAN Z F.Multigrid method based on the high accuracy full implicit scheme of the convection diffusion equation[J].Chinese Journal of Computational Mechanics,2004,21 (6):678-682.DOI:10.3969/j.issn.1007-4708.2004.06.007.

[12] 葛永斌,田振夫,吴文权.三维对流扩散方程的高精度全隐式多重网格方法[ J ].计算力学学报,2007,24 (2):181-186. GE Y B,TIAN Z F,WU W Q.Multigrid method based on high accuracy full implicit scheme of 3D convection diffusion equation[J].Chinese Journal of Computational Mechanics,2007,24 (2):181-186.DOI:10.3969/j.issn.1007-4708.2007.02.010.

(责任编辑：梁俊红)

High order compact difference scheme for the one-dimensional unsteady convection diffusion reaction equation

YANG Xiaojia,TIAN Fang

(School of Mathematics and Statistis Science,Ningxia University,Yinchuan 750021,China)

A two-level high order compact finite difference implicit scheme is proposed to solve the one-dimensional unsteady convection diffusion reaction equation.The local truncation error of the scheme is O(τ2+τh2+h4),i.e.the scheme is the fourth order accuracy for space when τ=O(h2).Then,Fourier analysis method is used to prove the stability of the scheme.Finally,numerical experiments are conducted to verify the accuracy and the reliability of the present scheme.

convection diffusion reaction equation;unsteady;compact difference scheme;implicit scheme;high accuracy

10.3969/j.issn.1000-1565.2017.01.002

2016-03-28

国家自然科学基金资助项目(11361045;11161036);宁夏大学自然科学基金项目资助(ZR15014);宁夏大学研究生创新项目(GIP201620)

杨晓佳(1988—)，女，宁夏吴忠人，宁夏大学在读硕士研究生，E-mail：yang_xiaoj@sina.com

田芳(1979—)，女，宁夏中宁人，宁夏大学副教授，主要从事偏微分方程数值解法的研究. E-mail：tianfsunny@126.com

O241.82

A

1000-1565(2017)01-0005-08