Oregonator模型中欠扩散斑图动力学
2017-03-14闫佳冯帆张永亮贺亚峰
闫佳,冯帆,张永亮,贺亚峰
(河北大学 物理科学与技术学院,河北 保定 071002)
Oregonator模型中欠扩散斑图动力学
闫佳,冯帆,张永亮,贺亚峰
(河北大学 物理科学与技术学院,河北 保定 071002)
利用时间分数阶微分Oregonator模型在Turing-Hopf切空间附近研究了欠扩散对斑图动力学的影响.通过傅里叶和拉普拉斯变换对系统做了稳定性分析,并进行了一维数值模拟.结果表明,活化子欠扩散时有利于抑制Turing模,增强Hopf模,而禁阻子欠扩散时则反之.研究结果对深入研究分形媒介中的斑图动力学提供了依据.
斑图动力学;傅里叶变化;反常扩散
斑图动力学是非线性科学研究的一个重要方向.掌握时空斑图形成机制对揭示生命的起源、开发治疗心颤的新方法、解释生态系统的诸多现象等都具有重要的现实意义[1].化学反应系统和Pt催化CO氧化反应系统是研究斑图动力学常用的实验系统[1-3],它们所呈现出的丰富的斑图动力学(如螺旋波等)通常用反应扩散模型来描述.这些模型假设分子间发生化学反应所需时间远小于分子扩散时间,并且反应物分子只向其最近邻以固定的时间间隔进行独立的空间扩散,即正常扩散情况.然而,对于化学反应中使用的溶胶和多孔玻璃等媒介,以及Pt催化CO氧化反应中的非均相Pt表面,它们通常具有分形结构,反应物分子在其中实际存在着反常扩散[4-10],因此,有必要对反常扩散情况下的斑图动力学进行深入研究.
正常扩散情况下斑图动力学一般用传统的整数阶反应扩散方程描述,而反常扩散情况下的斑图动力学则需要用分数阶反应扩散方程描述,利用时间分数阶微分(Caputo分数微分)描述欠扩散,利用空间分数阶微分(Riemann-Liouville分数微分)描述超扩散[5-8].分数阶反应扩散方程可以由统计动力学中的连续时间随机行走模型得到[11],它的分析与数值模拟比正常扩散时要复杂得多,这方面的研究正处于起步阶段.在欠扩散斑图动力学研究方面:Henry等[12-13]研究了欠扩散时的Gierer-Meinhardt模型和Brusselator模型,他们发现在欠扩散时图灵斑图形成条件也不一定要求阻滞子的扩散系数必须大于活化子的,图灵失稳时的扩散系数比随欠扩散指数降低.Gafiychuk等[14-16]主要讨论了欠扩散FitzHugh-Nagumo模型中图灵分叉与Hopf分叉过程.Barrio等[8]利用傅里叶与拉普拉斯变换方法分析了欠扩散时的图灵分叉条件,得到了同样的结论[8].本文利用时间分数阶Oregonator模型研究了Turing-Hopf切空间附近欠扩散斑图动力学,利用傅里叶与拉普拉斯变换进行了稳定性分析,讨论了扩散指数对Turing模与Hopf模的影响,并在一维空间进行了数值模拟.
1 模型分析与数值计算结果
考虑欠扩散2变量Oregonator反应扩散方程,欠扩散用时间分数阶微分描述:
(1)

(2)
其中,变量u和υ表示活化子和禁阻子浓度,Du和Dυ分别是对应的扩散系数,ε描述变量的反应速率,f、q为控制参数.扩散指数α、β分别表示活化子和禁阻子时间分数阶微分.
方程左边为Caputo分数微分,其定义为
(3)
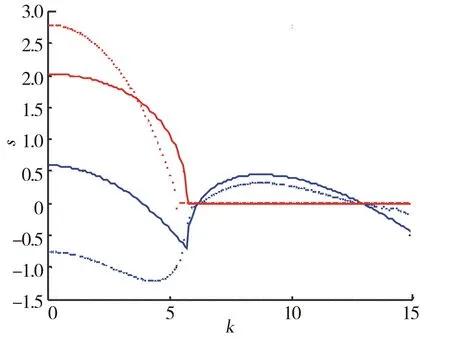
其中m-1<γ (4) (5) 其中,a11=(1-2u0-fυ02q/(u0+q)2)/ε,a12=f(u0-q)/(u0+q)/ε,a21=1,a22=-1,对(4)-(5)式做傅里叶和拉普拉斯变换得 sγU-sγ-1U(k,0)=a11U+a12V-Duk2U, (6) sγV-sγ-1V(k,0)=a21U+a22V-Duk2V, (7) 其中,U和V分别为 (8) (9) 解上式得 (10) (11) 其中 S(k,s)=sα+β+sα(Dvk2-a22)+sβ(Duk2-a11)-k2(Dva11+Dua22)+DuDvk4+a11a22-a21a12, (12) 显然,μ(k,t)的时间演化由U和V的奇点给出,即S=0.对于Turing模失稳需要满足Re[s0(k=0)]<0和Re[s0(k≠0)]>0.对于Hopf模失稳需要满足Re[s0(k=0)]>0和Im[s0(k=0)]≠0.为了研究Turing-Hopf切空间反常扩散斑图动力学,固定参数为Dμ=0.01,Dv=0.07,f=1.85,q=0.002,ε=0.15.由于时间分数阶微分的计算具有时间记忆的特征,系统定态的数值计算需要非常大的内存,因此只在一维空间数值模拟欠扩散斑图动力学.数值模拟的时间步长为dt=0.001时间单位,空间步长为dx=0.06空间单位. 首先,研究只有禁阻子欠扩散时Turing-Hopf切空间的斑图动力学,即α=1,β<1.根据式(12),图1给出了系统色散关系,其中实线表示正常扩散时的色散曲线.由图1可见,在正常扩散时,Turing模和Hopf模均失稳.当禁阻子发生欠扩散时,随着扩散指数的减小,Hopf模的强度逐渐减小,Turing模比正常扩散时强度略增大.当β<0.82时,Hopf模小于零.Hopf模对应的振荡频率随β减小而减小,因此,减小扩散指数β可以抑制Hopf模,增强Turing模. a.β=0.4,α=1;b.β=0.6,α=1;c.β=0.8,α=1; 实线(虚线)对应正常(反常)扩散. 图2给出了α=1时的一维数值模拟结果,其中横轴表示时间,纵轴表示空间.由图1可知,当β=0.4、0.6时,系统的Hopf模实部小于零,Turing模大于零,因此系统出现稳定的Turing斑图,如图2a、b所示.当α=β=1时,反应物正常扩散,Hopf模和Turing模均大于零且存在竞争,此时形成时空振荡斑图,如图2c所示. a.β=0.4,α=1;b.β=0.6,α=1;c.β=1,α=1; 横轴为时间,纵轴为空间,其他参数同图1. 下面讨论当只有活化子发生欠扩散时的斑图动力学.图3给出了β=1,α<1时的色散关系.由图3可见,随着扩散指数α的减小,Hopf模增强,Turing模减弱,系统振荡频率增加.这表明,活化子欠扩散有利于抑制Turing模,增强Hopf模,与上述禁阻子的作用相反.图4给出了α=0.7、0.8、0.9时系统的时空演化,由于此时Hopf失稳,因此系统出现空间均匀时间振荡,且振荡频率随减小而增加. a.α=0.4,β=1;b.α=0.6,β=1;c.α=0.8,β=1; 实线(虚线)对应正常(反常)扩散. a-c中α=0.7、0.8、0.9,β=1,其他参数同图3. 反常扩散指数α=β=0.7; 实线(虚线)对应正常(反常)扩散. 图5 色散关系 以上2种情况分别考虑了只有活化子或只有禁阻子发生欠扩散时对系统动力学的影响.当反应物分子在反应媒介中具有相同的欠扩散特性时,考虑活化子和禁阻子的扩散指数相同,即α=β≤1.此时,系统的色散关系如图5所示,其中的实线表示正常扩散时的色散曲线.由图5可见,与正常扩散相比,当活化子和禁阻子存在相同的欠扩散时,系统的Hopf模降低,振荡频率增加,Turing模也有所减弱. 利用时间分数阶Oregonator模型在Turing-Hopf切空间附近研究了欠扩散斑图动力学,通过傅里叶与拉普拉斯变换对系统进行了稳定性分析,讨论了扩散指数对Turing模与Hopf模的影响,并在一维空间进行了数值模拟.结果表明,活化子欠扩散时有利于抑制Turing模,增强Hopf模,而禁阻子欠扩散时则反之.如果同时考虑活化子和禁阻子欠扩散,即α=β≤1,则欠扩散更大程度上是抑制Hopf模,改变系统的振荡频率,同时对Turing模也有一定的影响. 化学反应系统中反应物分子欠扩散时,其扩散速度低于正常扩散时的速度.在Oregonator模型中可以用小扩散系数或时间分数阶微分来描述较慢的扩散过程.禁阻子欠扩散时,Turing模得到增强,等效于正常扩散时增加禁阻子的扩散系数.因此,与正常扩散相比,当禁阻子欠扩散时,禁阻子扩散系数不一定要比活化子的扩散系数大.这意味着,在分形媒介中,即使活化子与禁阻子的扩散系数相同时,仍然有望得到Turing斑图.笔者研究结果对深入研究Pt催化CO氧化反应与分形媒介化学反应实验中时空斑图形成机理提供了理论与数值依据. [1] 欧阳颀.非线性科学与斑图动力学导论[M].北京:北京大学出版社,2010. [2] BANSAGI JR T,VANAG V K,EPSTEIN I R.Tomography of reaction-diffusion microemulsions reveals three-dimensional Turing patterns [J].Science,2011,331:1309.DOI:10.1126/science.1200815. [3] SACHS C,HILDEBRAND M,VOLKENING S,et al.Spatiotemporal self-organization in a surface reaction:from the atomic to the mesoscopic scale [J].Science,2001,31:1635.DOI:10.1126/science.1062883. [4] 辛厚文.分形介质反应动力学[M].上海:上海科技教育出版社,1997:18. [5] METZLER R,KLAFTER J.The random walk's guide to anomalous diffusion:A fractional dynamics approach [J].Phys Rep,2000,339:1.DOI:10.1103/PhysRevE.62.2555. [6] DRAZER G,ZANETTE D H.Experimental evidence of power law trapping time distributions in porous media [J].Phys Rev E,1999,60:5858.DOI:10.1103/PhysRevE.60.5858. [7] WEEKS E R,WEITZ D A.Subdiffusion and the cage effect studied near the colloidal glasstransition,Chem [J].Phys,2002,284:361.DOI:10.1103/PhysRevLett.89.095704. [8] HERNANDEZ D,VAREA C,BARRIO R A.Dynamics of reaction diffusion systems in a subdiffusive regime [J].Phys Rev E,2009,79:026109.DOI:10.1103/PhysRevE.79.026109. [9] GAFIYCHUKV V,DATSKO B Y.Stability analysis and oscillatory structures in time-fractional reaction-diffusion systems [J].Phys Rev E,2007,75:055201.DOI:10.1103/PhysRevE.75.055201. [10] BERTRAM M,MIKHAILOV A S.Pattern formation on the edge of chaos:Mathematical modeling of CO oxidation on a Pt(110) surface under global delayed feedback[J].Phys Rev E,2003,67:036207.DOI:10.1103/PhysRevE.67.036207. [11] HENRY B I,LANGLANDST A M,WEARNE S L.Anomalous diffusion with linear reaction dynamics:From continuous time random walks to fractional reaction-diffusion equations[J].Phys Rev E,2006,74:031116.DOI:10.1103/PhysRevE.74.031116. [12] HENRY B I,LANGLANDS T A M,WEARNE S L.Turing pattern formation in fraction activator-inhibitor systems [J].Phys Rev E,2005,72:026101.DOI:10.1103/PhysRevE.72.026101. [13] LANDLANDS A M,HENRY B I,WEARNE S L.Turing pattern formation with fractional diffusion and fractional reactions [J].Phys Condens Matter,2007,19:065115.DOI:10.1088/0953-8984/19/6/065115. [14] GAFIYCHUK V V,DATSKO B Y.Spatiotemporal pattern formation in fractional reaction-diffusion systems with indices of different order[J].Phys Rev E,2008,77:066210.DOI:10.1103/PhysRevE.77.066210. [15] GAFIYCHUK V V,DATSKO B Y.Pattern formation in a fractional reaction-diffusion system [J].Physica A,2006,365:300.DOI:10.1016/j.physa.2005.09.046. [16] DASTKO B Y,GAFIYCHUK V V.Self-organization phenomena in reaction diffusion systems with non-integer order time derivatives [J].Phys Scr,2009,136:014027.DOI:10.1088/0031-8949/2009/T136/014027. (责任编辑:孟素兰) Pattern formation induced by subdiffusion in Oregonator model YAN Jia,FENG Fan,ZHANG Yongliang,HE Yafeng (College of Physics Science and Technology,Hebei University,Baoding 071002,China) Effect of subdiffusion on the dynamics of pattern formation is studied near codimension-two Turing-Hopf bifurcations in a fractional-in-time Oregonator model.Stability analysis is performed by using Fourier and Laplace transforms,and numerical simulations are conducted in one dimension.Our results have shown that the subdiffusion of activator can depress Turing mode and promote Hopf mode.In the case of subdiffusion of inhibitor,the results are reversed.The results obtained here are helpful to the intensive study of pattern formation in fractal media. pattern formation;Fourier transform;anomalous diffusion 10.3969/j.issn.1000-1565.2017.01.004 2016-04-14 国家自然科学基金资助项目(11205044,11405042);河北省自然科学基金资助项目(A2011201006;A2012201015);河北省教育厅基金资助项目(Y2012009);中西部高校综合实力提升工程;河北大学科学研究基金资助项目 闫佳(1991—),男,陕西麟游人,河北大学在读硕士研究生,主要从事斑图动力学方面研究. E-mail:245323970@qq.com 贺亚峰(1978—),男,河北阳原人,河北大学副教授,主要从事斑图动力学方面研究.E-mail:heyf@hbu.edu.cn O415 A 1000-1565(2017)01-0019-05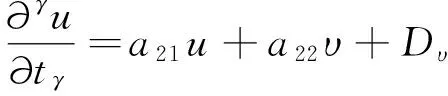





2 结论
