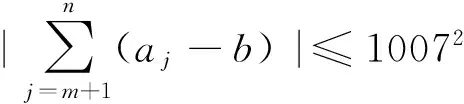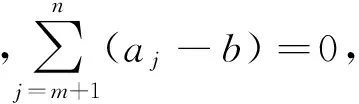两道奥数题的简洁解法

湖南省湘西州民族中学 (416000) 刘文生

两道奥数题的简洁解法

湖南省湘西州民族中学 (416000) 刘文生

本文给出2015年国际奥林匹克第5题与第6题的简洁解法，供大家参考.

第5题 设R是全体实数的集合，求所有的函数f:R→R，满足对任意实数x,y，都有f(x+f(x+y))+f(xy)=x+f(x+y)+yf(x)(1)

解：当x=y=0时，由(1)得f(f(0))=0.据此，当x=0,y=f(0)时，f(x+y)=f(f(0))=0，此时，(1)式成为f(0)+f(0)=f(0)f(0).

由此得f(0)=0或f(0)=2,当f(0)=0时，令y=0，由(1)可知，对任意实数x，有f(x+f(x))=x+f(x)，显而易见，f(x)=x.当f(0)=2时，f(2)=f(f(0))=0，令y=0，由(1)可知,对任意实数x，有f(x+f(x))+2=x+f(x).

显而易见x+f(x)=2，即f(x)=2-x.由上可知，所求函数为f(x)=x与f(x)=2-x.

第6题 整数序列a1,a2,……满足下列条件：

(1)对每个整数j≥1，有1≤aj≤2015;

(2)对任意整数1≤k

证明：由(1)对每个整数j≥1，有1≤aj≤2015可知，存在正整数N,使得aN=2015.由(2)可知l>k时，al≥ak(由k+ak≠l+al，即al-ak≠k-l<0,所以al-ak≥0,al≥ak).

由上可知，题设中的10072可以改为任意的非负数.