例析二次函数零点式在解题中的妙用

浙江省湖州二中 (313000) 胡志杰

例析二次函数零点式在解题中的妙用

浙江省湖州二中 (313000) 胡志杰

二次函数内容是高中数学教学的重点之一，也是历年高考必考考点之一.而对于二次函数的认识，许多人仅仅停留在一般式y=ax2+bx+c(a≠0)与顶点式y=a(x-h)2+k(a≠0)上，却忽略了它的另一种重要的零点式y=a(x-x1)(x-x2)(a≠0).在解决函数问题时，解题方法的选择尤为重要，恰当的方法可助考生节时省力，秒杀考题，并常让人有“柳暗花明又一村”的感慨.

一、妙解函数题

例1 (2016湖州市高中数学竞赛第17题)已知二次函数f(x)=x2+bx+c(b,c∈R).若方程f(x)=0在[0,1]上有两个实数根，求b+c的取值范围.

分析：考生反映该题解答费时，多数考生采用的方法是线性规划，确实有点“烦”.若能观察到f(1)中含有b+c，再配合零点式，即可妙解此题.设f(x)的两个零点分别为x1,x2，则f(x)=(x-x1)(x-x2)，不妨设x1∈[0,1],x2∈[0,1].因为f(1)=(1-x1)(1-x2)，且1-x1∈[0,1],1-x2∈[0,1]，所以f(1)=1+b+c∈[0,1]，所以b+c∈

[-1,0].

例2 (2016年稽阳联考第17题)已知关于x的方程ax2+bx+c=0(a>0,b,c∈R)有实数根且均在区间(0,2)内.若c≥1,25a+10b+4c≥4，求a的最小值.

二、妙解不等式

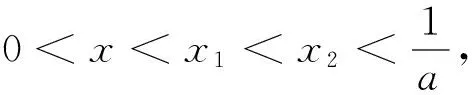
(1)若f(x)在x=1和x=3处取得极值,试求b、c的值；

(2)若f(x)在x∈(-∞,x1),(x2,+∞)上单调递增且在x∈(x1,x2)上单调递减,又满足x2-x1>1,求证：b2>2(b+2c)b；

(3)在(2)的条件下，若t

分析：(1)(2)略，(3)以三次函数作背景，通过导函数对应的方程转化为一元二次方程根与系数关系，化系数为根表示，利用根所满足条件使问题得证.

f′(x)=x2+(b-1)x+c，在(2)的条件下设x2+(b-1)x+c=(x-x1)(x-x2)即x2+bx+c=(x-x1)(x-x2)+x，所以(t2+bt+c)-x1=(t-x1)(t-x2)+t-x1，∵x2>1+x1>1+t，∴1+t-x2<0，∵00，即t2+bt+c>x1.

三、妙解解析几何

例5 (2012年重庆卷)这椭圆的中心为原点O，长轴在x轴上，上顶点为A，左右焦点分别为F1、F2，线段OF1，OF2的中点分别为B1、B2，且ΔABC的面积为4.

(1)求该椭圆的离心率和标准方程；

(2)过B1做直线l交椭圆于P、Q两点，使PB2⊥QB2，求直线l的方程.

分析：本题传统思路是设直线方程后与椭圆方程联立，并通过韦达定理得到x1+x2、x1x2，代入PB2⊥QB2条件后进行求解.然读者若进行验算即可发现，其化简过程极其繁琐，在考试限时环境下难以完成，若采用二次函数零点式可大大降低化简难度.

(2)易得B1(-2,0)，B2(2,0).

当l⊥x轴时，显然不成立；当l不垂直于x轴时，设l=k(x+2)，P(x1,y1),Q(x2,y2),由PB2⊥QB2，得(x1-2)(x2-2)+y1y2=0⟹(x1-2)(x2-2)+k2x1x2=0①,

事实上，在解析几何中，只要有PA⊥PB的条件翻译后(其中P为已知点，A、B为直线与曲线的交点)，就可以用二次函数零点式简化过程.

本文笔者所提到的方法，并不是追求高难度的解题技巧，而是着意于解题工具的选择，着意于数学问题的理解，揭示数学本质，看出题目的结果.在实际操作中，读者需多种方法双管齐下，方可所向披靡.

[1]叶兴炎，二次函数零点式：平凡亦不凡[J].中学数学教学，2015,1(39).

[2]高考数学研究组，浙江高考数学2014一路走来——浙江省高考数学解析[M].浙江：浙江大学出版社，2016.