一道2015年四川赛区预赛题推广

江苏省姜堰中等专业学校 (225500) 孙春扣 陈 宇

一道2015年四川赛区预赛题推广

江苏省姜堰中等专业学校 (225500) 孙春扣 陈 宇

2015年全国高中数学联赛四川赛区预赛第15题：

证明：(1)直线l与双曲线只有一个交点；

(2)⊿OAB的面积为定值.

经过探究，笔者发现，这道赛题可以推广到一般形式.即

证明：(1)直线l与双曲线C只有一个交点；

(2)⊿OAB的面积为定值.

证明：当点P(x0,y0)为右支上任意一点时，

设过点P(x0,y0)的直线l的斜率为k.

(*)与①的斜率相同，且同过P(x0,y0)，可见(*)与①表示同一直线.即直线l为双曲线上过P(x0,y0)处的切线(这里若依参考答案的解法，则较繁).∴直线l与双曲线只有一个交点.

(2)ⅰ)当k不存在时，由(1)ⅰ)可知|OA|·

当a=1,b=2时，即为原赛题.

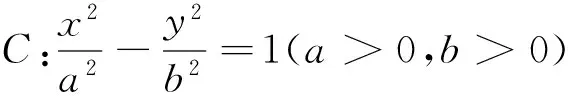
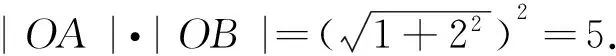
当然，由上述推广所得之结论，令a=1,b=2，亦可验证文[1]的参考答案(2)是错误结果—这显然是计算错误.

进而，推广之问题(1)存在逆命题.

同理yA+yB=2y0,∴P为AB的中点.(这里，直线l与双曲线C的实轴是否垂直，均已包含于上述证明中.当y0=0时，k不存在，直线l的方程为x=x0=a).

且此时不影响问题(2)的成立—即⊿OAB的面积为定值.

在圆锥曲线中，渐近线为双曲线所独有.故此充要条件亦为双曲线所独有.不可类比到椭圆和抛物线.

[1]2015年全国高中数学联赛四川赛区预赛.中等数学,2016,7.