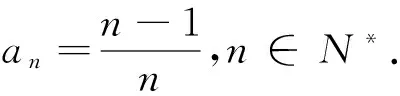赏析“新定义型”数列
2017-03-13浙江省金华市第六中学321000胡奇宝
浙江省金华市第六中学 (321000) 胡奇宝
赏析“新定义型”数列
浙江省金华市第六中学 (321000) 胡奇宝
近年来,全国各地高考试题或各地模拟试题中出现了一种“新定义型”数列,这种数列问题情境新颖,阅读量明了简短,让答题者眼前一亮的同时犹如一股清新之风迎面吹来,令人神清气爽.在领略了题目的真意之后,更体会到了命题人的匠心独具和创新精神.
“新定义型”数列给出一种不同于常规的新概念、新性质、新运算、新符号,旨在考查学生对数学基础知识、基本方法、基本技能的掌握情况,而且考查了学生的创新思维能力.正是由于这种总揽各种知识方法、能力的特点使得“新定义型”数列,如同一朵清新的小花成为全国各地考题的新宠.现采撷几朵与同行交流欣赏,不妥之处请批评斧正.
一、无穷互补数列
题1 对于无穷数列{an}与{bn},记A={x|x=an,n∈N*,B={x|x=bn,n∈N*},若同时满足条件:①{an},{bn}均单调递增;②A∩B=∅且A∪B=N*,则称{an}与{bn}是无穷互补数列.
(1)若an=2n-1,bn=4n-2,判断{an}与{bn}是否为无穷互补数列,并说明理由;
(2)若an=2n且{an}与{bn}是无穷互补数列,求数列{bn}的前16项的和;
(3)若{an}与{bn}是无穷互补数列,{an}为等差数列且a16=36,求{an}与{bn}的通项公式.
解析:(1)因为4∉A,4∉B,所以4∉A∪B,从而{an}与{bn}不是无穷互补数列.
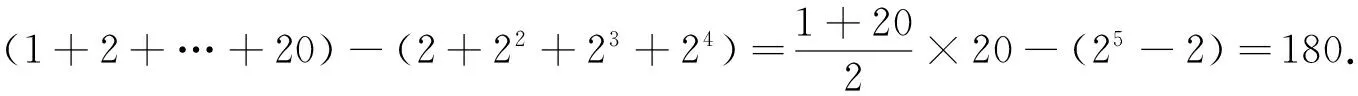
(3)设{an}的公差为d,d∈N*,则a16=a1+15d=36.
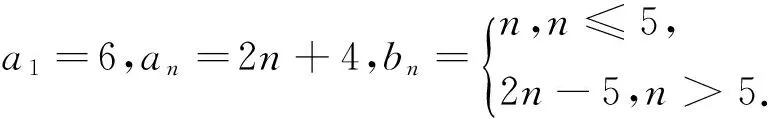
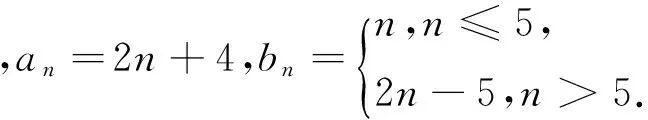
评注:要证明一个结论不正确,只要举出一个反例即可,而要证明结论正确,必须经过严格的推理论证.
二、H数列
题2 设数列{an}的前n项和为Sn,若对任意正整数n,总存在正整数m,使得Sn=am,则称数列{an}是“H数列”.
(1)若数列{an}的前n项和Sn=2n(n∈N*),证明: 数列{an}是“H数列”;
(2)设数列{an}是等差数列,其首项an=1,公差d<0.若{an}是“H数列”,求d的值;
(3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立.
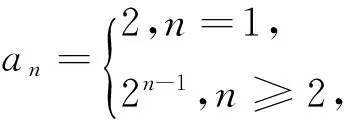
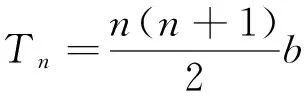
评注:本题简洁明了,计算并不复杂,着力考查学生探究能力、推理论证能力.把一个等差数列“分解”成两个“H数列”,就构造适合条件的数学对象而言,本身就蕴涵着创造,“分解”答案不唯一,这正是本题的魅力所在.
三、T数列
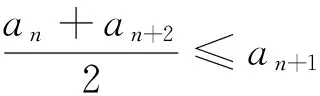
(1)若an=-n2+9n,(n∈N*),证明:数列{an}是T数列;
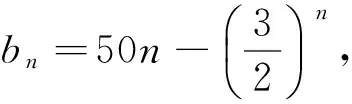
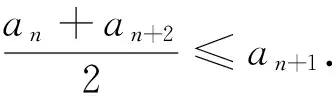
综上,数列{an}是T数列.
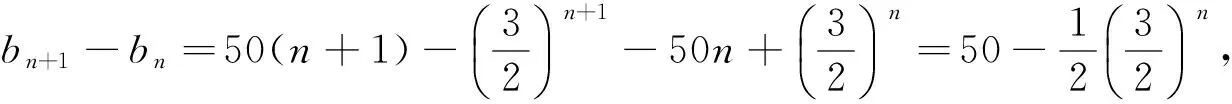
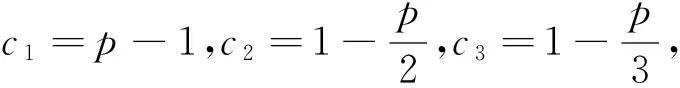
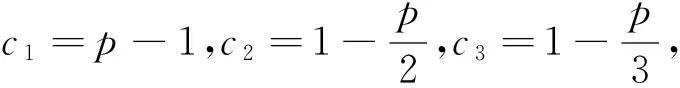
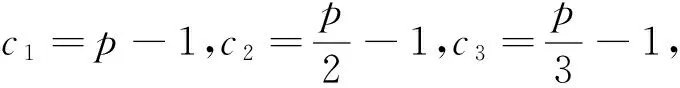
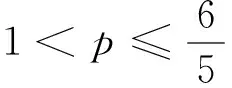
评注:本题背景新颖,设问流畅,层次感强.命题者设计了关联程度高的三个问题,使本题有较强的区分度、效度和信度.第一小问是新定义数列的简单应用;第二小问是给出一个具体数列,满足T数列的条件,求出参数M的取值范围;第三小问则要求解题者能够灵活使用作差法,熟练运用分类讨论的数学思想方法,有一定的难度.
四、p-摆动数列
题4 定义数列{xn},如果存在常数p,使对任意正整数n,总有(xn+1-p)(xn-p)<0成立,那么我们称数列{xn}为“p-摆动数列”.
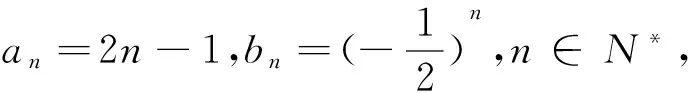
(2)设数列{cn}为“p-摆动数列”,c1>p,求证:对任意正整数m,n∈N*,总有c2n (3)设数列{dn}的前n项和为Sn,且Sn=(-1)n·n,试问:数列{dn}是否为“p-摆动数列”,若是,求出p的取值范围;若不是,说明理由. 解析:(1)假设数列{an}是“p-摆动数列”,即存在常数p,总有2n-1 (2)由数列{cn}为“p-摆动数列”,c1>p,即存在常数p,使对任意正整数n,总有(cn+1-p)(cn-p)<0成立.即有(cn+2-p)(cn+1-p)<0成立.则(cn+2-p)(cn-p)>0,所以c1>p⟹c3>p⟹…⟹c2n+1>p,同理(c2-p)(c1-p)<0⟹c2 (3)当n=1时,d1=-1,当n≥2,n∈N*时,dn=Sn-Sn-1=(-1)n(2n-1).综上,dn=(-1)n(2n-1),即存在p=0,使对任意正整数n,总有dndn+1=(-1)2n+1(2n-1)(2n+1)<0成立,所以数列{dn}是“p-摆动数列”; 当n为奇数时dn=-2n+1递减,所以dn≤d1=-1,只要p>-1即可,当n为偶数时dn=2n-1递增,dn≥d2=3,只要p<3即可. 综上-1 评注:从学习数列的角度看,强调数列是特殊的函数,就是说研究数列可以借鉴函数的方法来研究项(通项)与项数间的关系和项与项间的(递推)关系.本题既考查了两个特殊数列(等差、等比)及研究问题的方法,又考查了研究数列的核心问题(通项、递推).以课本摆动数列的定义为线索,改变题目原有的呈现形式,来实现对教材中问题的适当延伸或拓展. 所以,当-n2+5>0⟹n≤2时,|bn+1|>|bn|;同理可得,-n2+5<0⟹n≥3时,|bn+1|<|bn|.即数列{|bn|}在n=1,2,3时,递增;n≥4时,递减;即|b3|是数列{|bn|}的最小值. 评注:本题以“ω域收敛数列”为载体,融合了数列单调性﹑分类讨论等知识与思想方法,着重考察了学生阅读、分析、理解能力,是一道不可多得的新定义型试题. 后记:以上“新定义型”数列题考查了学生阅读和理解能力,同时考查了学生对新知识、新事物接受能力和加以简单运用的能力,考查了学生探究精神.要求解题者通过观察、阅读、归纳、探索进行迁移,即读懂和理解新定义,获取有用的新信息,然后运用这些有效的信息进一步推理,综合运用数学知识解决问题的能力和探索能力(多想少算甚至不算).因此,“新定义型”数列在高考中常有体现,是一种用知识归类、套路总结、强化训练等传统教学方法却难以解决高考中不断出现的新颖试题.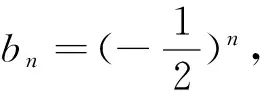
五、ω域收敛数列