数学习题教学中学生短视性思维的表现、成因及解决对策

【摘要】在问题解决过程中，由于学生原有知识系统中的思维定势、知识倾向、关系错位等，学生往往会出现短视性思维错误，如认识问题不够深入、考虑问题不够全面等，这将限制他们的思考方式，造成他们数学反思能力的缺失。在教学中，教师应分析学生在问题解决中出现短视性思维错误的原因，积极寻找解决对策，并设法避免这种现象的出现。

【关键词】短视性思维；表现形式；成因分析；解决对策

【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009（2016）44-0027-03

【作者简介】翟建毅，江苏省连云港师专一附小教育集团龙河校区（江苏连云港，222006），一级教师。

习题教学是辅助学生巩固知识的有效手段，是检验学生知识掌握情况的有效途径，起到沟通课堂学习与课后练习的作用。教师在习题教学中往往过分追求习题的正确率，而忽视了学生已有的思维定势、知识倾向、关系错位以及因此形成的短视性思维错误，如计算7×20÷7×20时，有很多学生会将答案错算成1。在教学中，教师应重视学生习题演算中出现的短视性思维错误，认真分析其成因，积极寻找解决对策。

一、学生短视性思维的特征及成因

小学阶段是学生思维发展的关键期，在这个阶段，其思维以形象思维为主，并逐步向抽象思维转化。在数学学习中，小学生容易出现认识问题肤浅，考虑问题不全面、不周密，不能跳出问题陷阱的漏解、多解、误解等短视性思维障碍。

（一）学生短视性思维特征辨析

短视性思维主要具有以下几个特征：一是学生不能全面地认识数学知识，无法形成严密的知识系统；二是因缺少严密的知识系统，学生存在模仿性思维；三是学生缺少反思能力，无法根据已有的知识经验完善认知。

（二）学生短视性思维成因辨析

1.思维定势导致短视性思维。

学生知识系统的形成有两条路径：一是教师帮助学生根据相关的知识点进行整理；二是学生根据自己已有的知识经验累积而成。在教学中，学生往往会形成思维定势，根据自己的知识系统分析问题，而忽视教师对自己知识系统的整合作用。因此，学生在习题练习中容易忽视题型的变化，从而出现计算错误。

例如：7×20÷7×20=1，学生会犯这种错误不是因为审题不清，而是他们对简便运算的理解不深入，仍然停留在简便运算的形式上，停留在局部，而忽视了它的实质，忽视了整体运算顺序，从而导致他们出现了短视性思维错误。

2.知识倾向造成短视性思维。

学生形成知识倾向主要有三方面原因：一是学生在学习过程中不断地积累知识，形成了自己的思维场；二是学生受到教师讲解和同学思维的影响，形成了思维倾向；三是学生受到教材中概念限定的影响。

例如：如图1所示，正方形的面积是8平方厘米，求圆的面积。知识倾向使学生思考问题呈现出片面、局部的特点，认为求圆的面积必须知道圆的半径或直径，而忽視了图形整体的联系，没有分析圆的半径和正方形的面积之间的关系，从而出现了短视性思维错误。

3.关系错位导致短视性思维。

小学低年级的数学问题中信息量较少，学生很容易理清题目中条件之间的关系。随着年级的升高，题目中的信息变多，干扰信息随之出现，学生容易在问题解决中出现条件之间的关系错位，从而导致他们出现短视性思维错误。

例如：一块长方形菜地，长20米，宽16米，因为公路扩建，长减少了6米，宽减少了4米，菜地面积比原来减少了多少？信息之间的干扰使得学生梳理条件时出现了错位，从而错误地认为减少的面积就是长为6米、宽为4米的长方形的面积。

二、顺应学生思维习惯，引导其走出短视性思维误区

面对习题教学中学生出现的短视性思维错误，教师要结合错因分析，顺着学生的思维习惯寻找有效的应对策略，从而提高他们的问题解决能力，使他们理清习题中的关系，完善知识系统，走出短视性思维误区。

（一）在扩充中打破知识倾向，完善知识概念内涵

学生分析问题时容易忽视条件与问题之间的内在联系，在教学中，教师应引领学生从局部分析到整体把握问题，借助数形结合理清条件和问题之间的内在联系。

1.从局部到整体——由倾向走向全面。

教师应引导学生从局部入手分析问题，再从整体层面把握问题，引领学生由局部思维走向整体思维。

案例1：苏教版五下《圆的面积》

教学圆的面积练习题时，通过如图1所示的图形引导学生分析求圆的面积要添加哪些条件，并反问学生：如果不告诉你直径和半径，还能求出圆的面积吗？

引领学生先从局部开始，慢慢深入到整体，挖掘题目中隐含的数量关系，通过转化进行解答。教师激活学生的转化思想，避免了学生由于知识倾向而可能出现的短视性思维错误。

2.数形结合——由关系错位走向正位。

数形结合思想是一种重要的数学思想，是一种通过数与形的相互转化来解决数学问题的方法。教师要注重学生思维的纵向发展和横向发展，引导他们从多个角度去分析、思考，培养他们的数形结合思想。

案例2：苏教版四下《解决问题的策略：画图》

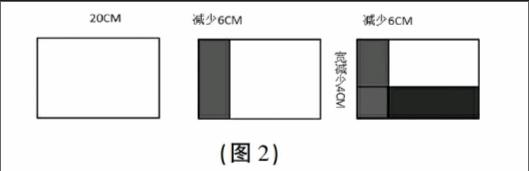
长方形的长是20厘米，宽是16厘米，如果长减少6厘米，宽减少4厘米，长方形的面积减少多少平方厘米？你能通过图形表示吗？

教学中引导学生画图（如图2），借助图形让问题从抽象走向直观，帮助学生理清题目中的数量关系。

教学中，教师结合学生的知识起点，适时渗透数形结合思想，把抽象的数学概念直观化，帮助学生由抽象转为直观，有效避免了学生因关系错位而出现的短视性思维错误。

（二）通过对比和描述深入理解计算法则，完善知识系统

为了让学生的知识系统与教师的知识系统有效连接，完善学生现有的知识系统，教师可以让学生在对比中理解基本计算方法，在文字描述中提高习题观察能力。

1.题组对比：理解基本计算方法。

学生在进行习题练习时，容易受到简便计算负迁移的干扰，从而形成短视性思维错误。针对学生的错误，教师提供题组对比，引导他们在题组支撑下分析运算法则，能在整体上提高学生的运算能力。

案例3：苏教版四下《运算律》

①25×4+25×4 ②25×4-25×4

③25×4÷25×4 ④25×4×25×4

⑤（25×4）+（25×4） ⑥（25×4）-（25×4）

⑦（25×4）÷（25×4） ⑧（25×4）×（25×4）

引导学生发现题组之间的异同和内在联系，使他们的知识系统在题组对比中得到强化。从整体上分析习题，有助于提高学生的运算能力和发散思维能力，能有效消除学生因为简便计算负迁移引发的短视性思维错误。

2.文字描述：提高学生对式题的观察能力。

学生的式题错误率普遍偏高，追寻其原因，教师发现，学生往往从局部分析问题，容易看错运算符号和数字。在教学中，教师可以引领学生用文字描述习题，以提高他们对习题的观察能力。

案例4：苏教版四下《运算律》

师：25×4+25×4，谁能用文字描述这道题？

大部分学生用直来直去的方式“读”习题，而忽略了习题的运算顺序。

文字描述这一方式最初给教学带来了一定的阻力，大部分学生不能完整地描述式题，但是经过一段时间的训练，学生对式题的观察能力明显增强，读题和解题的正确率也随之提高。

（三）培养良好的思维习惯，提升数学思维水平

良好的思维习惯是学生学好数学的关键，所以，教师应注重学生思维习惯的引导和培养。例如：在数学学习中经常会用到“数”，如数角、数线段、数图形等。一些学生在“数”的过程中没有养成良好的有序思维的习惯，局限于图形表面，从而会出现遗漏或重复的现象。

案例5：苏教版二下《角的初步认识》

让学生数图3中有多少个角时，有不少学生出現了重复或遗漏的现象。

教学中通过课件展示，先逐个呈现5小角，然后隐去两个小角公用的一条边，组成一个大角。

小学生由于缺少有条理的思维方式，往往会忽视图形内部的联系，仅从表面去数。通过引领学生从表面分析，再引领他们结合图形的内在联系进行整体分析，能让学生的思维从无条理走向有条理，从而使他们有效避免短视性思维错误的出现。

根据学生习题中出现的短视性思维错误现象，认真分析其成因、总结经验后，笔者认为，在教学中，要避免学生出现短视性思维错误，教师必须做好两点：一是关注学生的错误点，顺应学生的思维，倾听学生的声音，引领学生发现问题，培养学生“慢思”“慢想”的习惯，引领学生感悟知识背后的思想方法，从不同角度、不同层次理解问题，完善学生的思维场。二是结合学生的知识起点，分析教材中哪些知识点容易让学生产生思维定势、知识倾向、关系错位，努力寻找适合学生的教学方法，培养他们的探究能力。

注：本文获2015年江苏省“教海探航”征文竞赛一等奖，有删改。