地震静校正的相对时延法*

杨华臣， 康佳语， 张建中

(中国海洋大学海底科学与探测技术教育部重点实验室，海洋地球科学学院，山东 青岛 266100)

地震静校正的相对时延法*

杨华臣， 康佳语， 张建中**

(中国海洋大学海底科学与探测技术教育部重点实验室，海洋地球科学学院，山东 青岛 266100)

折射波时延法假设折射层速度横向变化不大和折射面起伏不大，且同时求取炮点和接收点的延迟时间，存在“此消彼长”的问题。针对这些问题，提出了折射波相对时延法。利用共炮点道集相邻接收点的折射波时差和共接收点道集相邻炮点的折射波时差，实现了炮点相对延时和接收点相对延时的独立求取，并利用已知控制点上的绝对延时或基准面静校正值，结合基点网平差方法，把相对延时转成绝对延时或基准面静校正量。同时，通过对相邻两道记录进行互相关确定相邻道的折射波时差，避免了低信噪比地震资料连续追踪同一折射层来拾取初至时间的困难。对理论模型合成数据和实际资料的测试表明，相对时延法克服了常用时延法的不足，对折射层速度变化和折射面起伏有较强的适应性。

折射波；相对时延法；时延法；静校正；近地表

静校正是提高地震成像质量的重要技术，也是复杂近地表地区地震资料处理的技术难点和研究重点之一[1]。在近几十年里，国内外地球物理工作者提出了许多的静校正方法。基于地震折射波初至走时的折射静校正方法[2-7]是被广泛使用的有效的静校正技术，大致可分成绝对折射静校正技术和相对折射静校正技术[8-10]。绝对折射静校正技术，如时延法[11](delay-time method,DTM)、ABC法[12]、广义互换法[13](generalised reciprocal method,GRM)、共中心点域折射静校正方法[14-16]，根据折射波走时方程，计算地表低速层产生的在炮点和接收点处的延迟时间；相对折射静校正技术，如相对折射静校正方法、改进的相对折射静校正方法，初至剩余静校正方法[17]，不直接使用折射初至时间，而是利用地震道之间的折射初至时间之差，或者各道初至时间与其拟合直线之差值，来求取炮点和接收点的相对初至时差或短波长的静校正量。这类方法不要求追踪同一折射层，主要用于解决短波长问题，对同一折射层初至走时难以追踪和拾取的地震资料，取得了良好的效果。

时延法是常用的折射波反演和折射初至静校正方法之一。Gardener于1939年提出时延法，Barthelmess、Wyrobek、Bernabini、Clement等人对该方法进行了发展和完善[18]。在二十世纪六七十年代，该方法被大量应用于深部地震折射剖面调查，Pakiser等人也将其应用于浅层勘察[19]。Bridle于2009年将该方法应用于Saudi Arabia某地区的三维静校正，并取得了良好的效果[20]。Mikesell等人于2012年提出了一种改进的时延法,并应用于二维模拟资料的静校正量的估计，也取得了很好的效果[21]。

时延法在假设折射层速度横向变化不大和折射层顶面起伏不大的情况下，同时计算出炮点和接收点的延迟时间，但计算炮点和接收点延迟时间存在“此消彼长”的问题。与其它绝对折射静校正技术一样，时延法也需要追踪同一折射层和拾取真正的初至走时，那么对于难以追踪同一折射层的地震记录，时延法的应用就受到限制。尽管现有相对折射静校正方法不需要追踪同一折射层，但不能考虑折射层速度的影响。为了解决时延法计算炮点和接收点延迟时间存在的“此消彼长”问题，以及折射界面起伏变化大和折射层速度横向变化大、同一折射层难以追踪等困难，本文提出了相对时延法(Relative delay-time method,RDTM)。

相对时延法也可认为是相对折射静校正技术的一种。它利用相邻地震道初至时间之差值，把炮点和接收点的延迟时间进行分离，分别独立计算相邻接收点之间的延迟时间和相邻炮点的延迟时间以及折射层的速度，并通过控制点上的基准面静校正量获取炮点和接收点的基准面静校正量。分别用时延法和相对时延法对模型合成数据和实际资料的处理结果表明，相对时延法计算结果更加准确，对近地表条件复杂地区折射界面起伏和高速折射层顶界面速度变化等复杂情况适应性更强。

1 相对时延法

如图1所示，当折射层速度为常数且顶面水平时，在炮点Sj激发，地震波沿箭头所示的路径传播，检波点Ri接收的折射旅行时可表示为[21]

(1)

其中：TSjRi是Sj点激发点Ri接收的折射波旅行时间;TSj是炮点Sj所对应的延迟时间;TRi是检波点Ri所对应的延迟时间;|Sj-Ri|是炮点Sj到检波点Ri的水平距离;W是折射波滑行慢度。

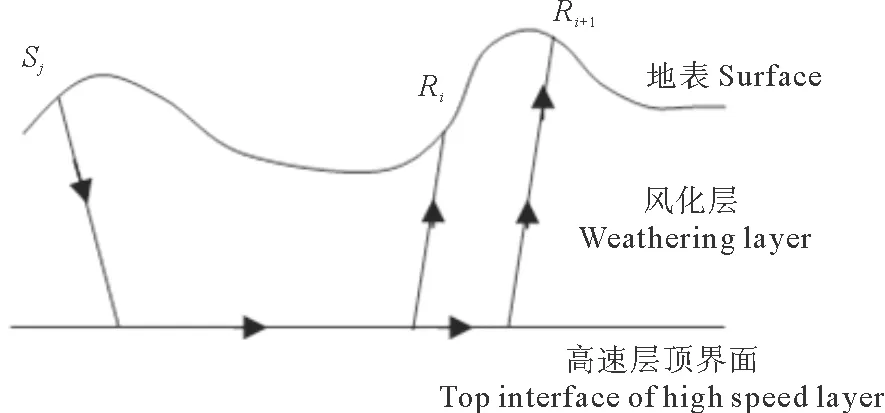
图1 折射波传播路径示意图

若有m个炮点，每炮n个检波点，将有m×n个形如(1)的方程，这样就形成下列矩阵方程：

Ax=T。

(2)

其中：T各个炮点检波点对的折射走时组成的向量，T=[TS1R1,TS1R2,…,TSmRn]；x为各个炮点和检波点的延迟时及折射层慢度组成的向量，x=[TS1,…,TSm,TR1,TR2,…,TRn,W]T；A是系数矩阵，

A=

求解(2)式就可以得到各炮点和检波点所对应的延迟时间以及高速折射层慢度，若知道上覆低速层速度，就可把延迟时间转化成低速层厚度。这就是常规的时延法。

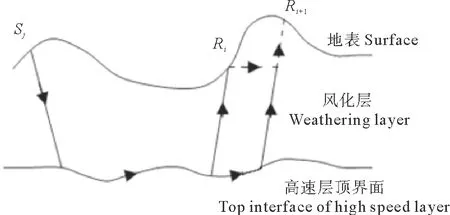
图2 折射波相对时差等效路径示意图

当折射层速度和顶界面深度变化较大时，如图2所示，上述方程则不严格成立。若在Sj点激发，在Ri和Ri+1点接收时，这两检波点接收到的折射波旅行时差可以表示为：

ΔTRiRi+1=TSjRi+1-TSjRi=dTRiRi+1+

(3)

其中：ΔTRiRi+1是指Ri+1点接收到的折射波旅行时与Ri点接收到的折射波旅行时之差，等价于地震波沿如图2中虚线所示路径，从Ri点到Ri+1点的旅行时；dTRiRi+1是点延迟时间与Ri点延迟时间之差，这里我们称其为相对延迟时间；Wi是Ri+1与Ri之间的高速折射层的慢度。该式消除了炮点Sj到接收点Ri之间的折射波走时，也即消除了炮点及其与Ri之间的折射面起伏和速度变化的影响。

在共炮点道集，各个相邻检波点折射走时之差都有消除了炮点延迟时间的方程(3)。在Ri+1相对于Ri的相对延迟时间与Ri相对于Ri+1的相对延迟时间的绝对值相等的假设下，我们利用这些方程，可以求出各个相邻检波点的相对延迟时间。对于m个炮点，每炮n个检波点的观测系统，根据最小二乘原理，建立下列约束优化问题：

其中：上式最后一项是对慢度的约束项；λ是约束系数；L是二阶差分拉普拉斯算子，L=(-1,2,-1)；wi是由三个相邻慢度组成的向量，wi=(Wi-1,Wi,Wi+1)。求解上述约束优化问题得

B·dT=ΔT。

(4)

在该式中，ΔT和B中的元素ΔTRiRi+1、ΔXi和λ均为已知量，dT中的元素dTRiRi+1和Wi为需要求解的未知量。

同样，在共检波点道集，相邻道走时之差可以消除检波点处的延迟时间，利用上述方法，就可以建立求炮点之间的相对延迟时间的方程。分别独立求解在共炮点道集和共检波点道集建立的上述方程，就可获得相邻检波点间的相对延迟时间、相邻炮点间的相对延迟时间和高速层速度。

2 相邻两道折射走时之差求法

如果直接拾取了折射波的初至时间，就可以用下式求取相邻道之间的初至走时之差：

ΔTRiRi+1=TSjRi+1-TSjRi。

(5)

其中：TSjRi是Sj点激发Ri点接收的折射波旅行时间，TSjRi+1是Sj点激发Ri+1点接收的折射波旅行时间，ΔTRiRi+1是指Ri+1点与Ri点接收到的折射波旅行时之差,即相当于从Ri点到Ri+1点的相对折射波旅行时。但当地震资料的信噪比低或者是可控震源资料时，初至波及其走时难以追踪和拾取，为此，本文通过计算相邻两道初至波之间的相关函数值[22-23]，直接求取相邻两道间的初至波相对时移量，作为相邻道初至走时之差。

3 静校正量计算

利用计算出的相对延迟时间，由已知点的基准面或浮动基准面静校正量可以求出其余点的基准面或浮动基准面静校正量[9-10]。当已知j点的静校正量后，i点的静校正量Ti为

(6)

式中dTk，k+1是相邻两点的相对延迟时间，即相邻炮点的相对延迟时间或相邻检波点的相对延迟时间。

当知道两个及以上点的静校正量时，利用类似于基点网平差的方法得到相邻已知静校正量点之间的所有点的静校正量。例如当已知j点和k点的静校正量Tj和Tk后，位于j和k点之间的i点的静校正量Ti为

(7)

4 理论模型实验

本文用上述的时延法和相对时延法对理论模型合成数据进行了试验。图3是低速层速度横向变化高速层速度不变的理论模型。模型由三层介质组成，长20000m，厚度约5 000m。在6000m以左地表水平，以右地表起伏，高程差最大可达150m。上层为低速层，速度在400m/s左右到1000m/s左右之间变化；中间层水平，速度为1500m/s，厚度为950m；第三层是速度为3000m/s的均匀层状介质。图4(a)是合成的炮点位于图3红色三角形处，以20m为道间距，从7500～13500m的单炮记录，可以看出，地表起伏和低速层速度变化对初至波和反射波走时有明显的影响。图5(a)是分别用时延法和相对时延法计算的该炮各接收点上的时间延迟与理论值的比较，相对时延法计算出的延迟时比时延法计算出的延迟时更加接近理论值。图5(b)是时延法和相对时延法计算结果的相对误差，整体来看，相对时延法计算结果的相对误差比时延法的更小。图6(a) 是分别用时延法和相对时延法反演出的第二层的速度与理论值的比较，相对时延法反演的结果虽然有所波动，但是总体而言，比时延法反演的结果更加接近理论值。把7500m处和13500m处的静校正量作为控制点上的已知静校正量，把计算的相对时延转换成绝对静校正值。图6(b)是时延法和相对时延法反演出的第二层的速度的相对误差。从图6(b)中可以更加明显的看出，相对时延法反演的第二层的速度的相对误差更小，其结果更加接近理论值。图4(b)和图4(c)分别是使用时延法静校正后和相对时延法静校正后的单炮记录，可以看出，使用两种静校正后，地形起伏和低速层速度变化对反射波和初至波的影响得到了明显消除，但相对时延法静校正后的结果更好一些。

(三角形表示炮点位置。The triangle indicatesshot position.)

(a)单炮记录;(b)时延法校正后的单炮记录;(c)相对时延法校正后的单炮记录

图5 静校正量(a)及其相对误差(b)对比

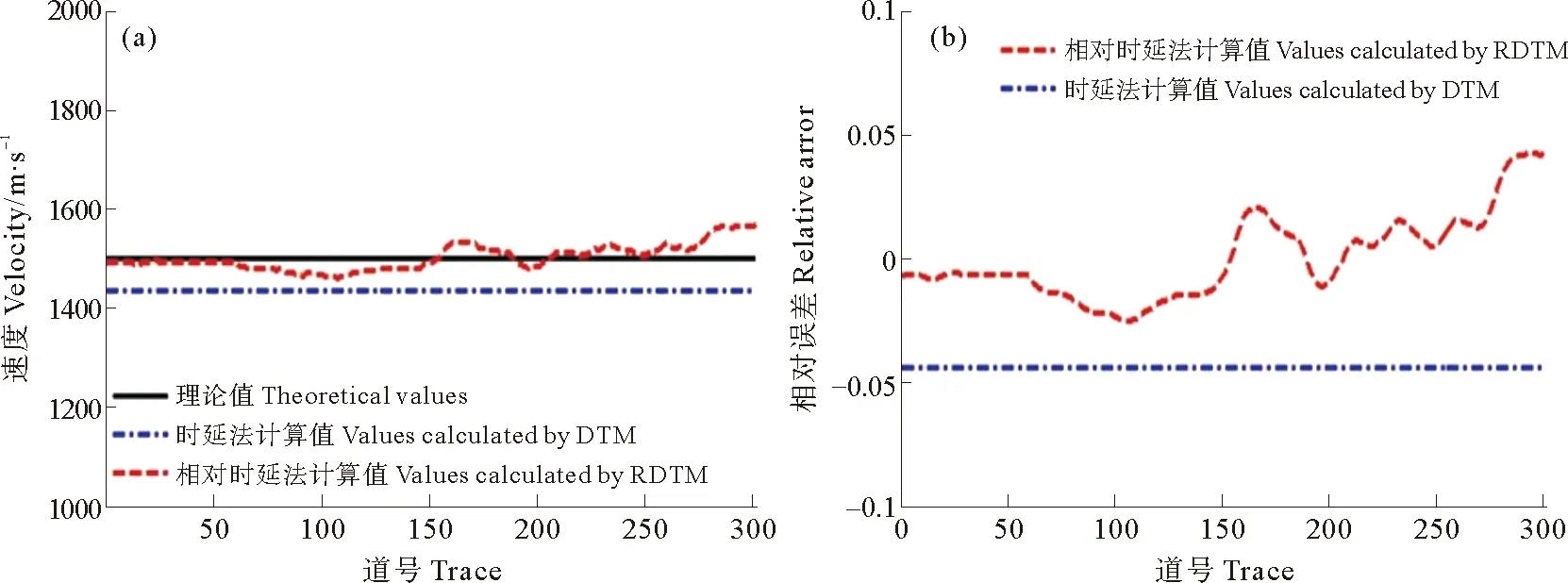
图6 反演折射层速度(a)及其相对误差(b)

图7是低速层速度和高速层速度同时横向变化且高速层折射界面起伏的理论模型。该模型除了第二层的速度在1600m/s左右到2400m/s左右之间变化和顶界面起伏，其余部分与模型1相同。图8(a)、(b)、(c)分别是静校正前的单炮记录、时延法静校正后的单炮记录和相对时延法静校正后的单炮记录。图9(a)是分别用时延法和相对时延法计算的该炮各接收点上的时间延迟与理论值的比较，相对时延法计算出的延迟时比时延法计算出的延迟时更加接近理论值。相对时延法计算出的静校正量比时延法计算出的静校正量的效果也更好。图9(b) 是分别用时延法和相对时延法反演出的第二层的速度与理论值的比较，相对时延法反演的速度十分接近理论值，而时延法反演的速度依然是常速。

(三角形表示炮点位置。The triangle indicatesshot position.)

(a)单炮记录;(b)时延法校正后的单炮记录;(c)相对时延法校正后的单炮记录

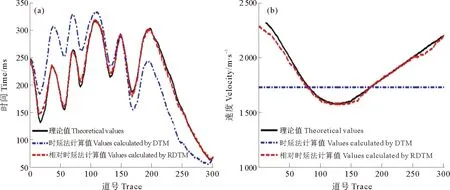
图9 计算静校正量(a)和反演折射层速度(b)对比

5 实际资料应用

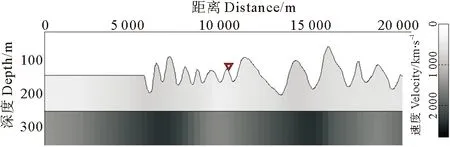
对中国新疆某戈壁区块的地震资料进行了静校正处理。该区域地表起伏较大，低速层较厚，资料的信噪比也很低。使用初至层析成像方法[1]建立了沿该测线的近地表速度模型，如图10所示，反映了该区近地表速度在横向和纵向的较大变化。分别用时延法和相对时延法计算了炮点和接收点基准面静校正量，其中，基准面高程为2 000m，替换速度为2 500m/s，用直达波走时统计计算的平均表层速度为1 388m/s。

图11、12和13分别是静校正前和利用时延法静校正及相对时延法静校正的叠加剖面。对比发现，静校正前剖面上，在CDP 250至CDP 345之间，时间2 000～2 200ms间的同相轴很模糊，时延法静校正剖面能够显现出连续同相轴，相对时延法静校正剖面的同相轴更加清楚，连续性更好，剖面质量得到了很大提高。这表明相对时延法解决复杂地区的静校正问题的良好效果。

图10 用初至层析建立的近地表速度模型

图11 未做静校正叠加剖面

图12 时延法静校正叠加剖面

图13 相对时延法静校正叠加剖面

6 结语

本文提出了一种折射波走时反演的相对时延法，克服了常用延时法同时求取炮点和接收点延迟时间存在的“此消彼长”的问题，对折射层速度变化和折射面起伏的情况有较强的适应性。理论模型合成数据和实际资料的处理表明，对于复杂近地表建模和静校正问题，相对时延法的效果良好，且优于常用的时延法。

致谢：在实际资料处理方面得到张一鸣、石太昆、金昌昆等的帮助，在此表示诚挚的谢意。

[1] Zhang J Z,Shi T K, Zhao Y S， et al. Static corrections in mountainous areas using Fresnel-wavepath tomography[J]. Journal of Applied Geophysics, 2014, 111: 242-249.

[2] 王克斌,赵灵芝, 张旭民. 折射静校正在苏里格气田三维处理中的应用[J]. 石油物探, 2004, 42(2): 248-251. Wang Kebin,Zhao Ling zhi,Zhang Xuemin.Application of refraction statics in 3-D data processing in Sulige gas field[J].Geophysical Prospecting for Petroleum, 2004, 42(2): 248-251.

[3] 林伯香,孙晶梅,徐颖,等. 几种常用静校正方法的讨论[J]. 石油物探, 2006, 45(4): 367-372. Lin Boxiang,SunJingmei,Xu Ying et al.Static correction approaches being frequently applied[J]. Geophysical Prospecting for Petroleum, 2006, 45(4): 367-372.

[4] 何光明,贺振华,黄德济,等. 几种静校正方法的比较研究[J]. 物探化探计算技术, 2006, 28(4): 310-314. He Guangming,HeZhenhua,HuangDeji et al.The comparison of several static’s correction methods[J].Computing Techniques for Geophysical and Geochemical Exploration, 2006, 28(4): 310-314.

[5] 段洪有,曾庆才,李琛. 复杂地表条件下折射静校正技术的应用[J]. 物探与化探, 2005, 29(2): 142-145. Duan Hongyou,Zeng Qingcai,Li Chen.The application of refraction static correction under complex surface conditions[J].Geophysical & Geochemical Exploration, 2005, 29(2): 142-145.

[6] Palmer D,Nikrouz R,Spyrou A. Statics corrections for shallow seismic refraction data[J]. Exploration Geophysics, 2005, 36(1): 7-17.

[7] Cox M J G,Scherrer E F, Chen R. Static Corrections for Seismic Reflection Surveys[M]. Tulsa: Society of Exploration Geophysicists, 1999:28-35.

[8] 郑鸿明. 折射波法相对静校正[J]. 石油地球物理勘探,1996, 31(3): 430-441. Zheng Hongming.Relative static correction using refraction wave[J].Oil Geophysical Prospecting, 1996, 31(3): 430-441.

[9] 陈广思. 相对折射静校正方法[J]. 石油地球物理勘探, 1990, 25(4): 407-428. Chen Guangsi.Relative refraction statics[J]. Oil Geophysical Prospecting, 1990, 25(4): 407-428.

[10] 潘宏勋,方伍宝, 武永山, 等. 改进的相对折射静校正方法[J]. 石油物探, 2004, 42(2): 208-211. Pan Hongxun,Fang Wubao,WuYongshan et al.An improved relative refraction statics technique[J]. Geophysical Prospecting for Petroleum, 2004, 42(2): 208-211.

[11] Burger HR. Introduction to Applied Geophysics[M].Portland:Scitech Book News,2006:2-8.

[12] 陈鹰鹏.地震数据折射波静校正方法研究[D].北京:中国地质大学(北京), 2011:12-15. ChenYingpeng.The Research of Seismic Data Refraction Static Correction Methods[D].Beijing： China University of Geosciences, 2011:12-15.

[13] Palmer D. An introduction to the generalized reciprocal method of seismic refraction interpretation [J]. Geophysics, 1981, 46(11): 1508-1518.

[14] 张建中, 戴云, 徐峰. 共中心点域折射静校正方法[J]. 石油地球物理勘探, 2001, 36(3): 297-300. Zhang Jianzhong,DaiYun,Xu Feng.A new method for refraction statics in CMP domain[J]. Oil Geophysical Prospecting, 2001, 36(3): 297-300.

[15] 张建中, 王克斌.一种三维折射初至静校正新方法[J]. 石油地球物理勘探, 2003, 38(6): 608-610. Zhang Jianzhong,Wangkebin.A new method of 3-D refracted first-break static correction[J]. Oil Geophysical Prospecting, 2003, 38(6): 608-610.

[16] 张建中, 徐峰, 戴云. 共中心点域浅层折射波解释方法及应用实例[J]. 石油地球物理勘探, 2001, 36(4): 459-465. Zhang Jianzhong,XuFeng,Dai Yun.Shallow refraction seismic interpretation method in CMP domain and its application case[J]. Oil Geophysical Prospecting, 2001, 36(4): 459-465.

[17] 刘连升. 约束初至拾取与初至波剩余静校正[J]. 石油地球物理勘探, 1998, 33(5): 604-610. Liu Liansheng. Constrained first-arrival pickup and first-break residual static correction[J]. Oil Geophysical Prospecting, 1998, 33(5): 604-610.

[18] 帕尔默. 折射地震学[M]. 北京： 地质出版社, 1989:55-57. Palmer D. Refraction Seismics[M]. Beijing:Geological Publishing House, 1989: 55-57.

[19] ZietzI, Pakiser L C. Note on an application of sonar to the shallow reflection problem[J]. Geophysics, 1957, 22(2): 345-347.

[20] BridleR. Delay-time refraction methods applied to a 3D seismicblock[J]. The Leading Edge, 2009, 28(2): 228-239.

[21] Mikesell T D, van W K,Ruigrok E et al. A modified delay-time method for statics estimation with the virtual refraction[J]. Geophysics, 2012, 77(6): A29-A33.

[22] 徐平, 王宝善, 张尉, 等. 利用互相关函数求地震波衰减[J]. 地球物理学报, 2006(6): 1738-1744. Xu Ping, Wang Baoshan, Zhang Wei, et al.Estimating seismic attenuation using cross-correlation function[J]. Chinese Journal of Geophysics, 2006(6): 1738-1744.

[23] 肖倩, 王建辉, 方晓柯, 等. 一种基于互相关函数的小波系数相关阈值去噪方法[J]. 东北大学学报(自然科学版), 2011(3): 318-321. Xiao Qian, Wang Jianhui, Fang Xiaoke, et al. A wavelet coefficient threshold denoising method based on a cross-correlation function[J]. Journal of Northeastern University(Natural Science), 2011(3): 318-321.

责任编辑 徐 环

The Relative Delay-Time Method for Seismic Statics

YANG Hua-Chen, KANG Jia-Yu, ZHANG Jian-Zhong

(The Key Lab of Submarine Geosciences and Prospecting Techniques, Ministry of Education, College of Marine Geosciences, Ocean University of China, Qingdao 266100, China )

Assuming that the lateral change of refractor velocity is small and the top surface of refractor is not highly rolling, refraction delay-time method estimates simultaneously source and receiver delay-times using traveltimes. There is trade-off between the source and receiver delay-times calculated by the delay-time method. In order to eliminate problems in delay-time method, we propose a relative delay-time method for inversion of refraction traveltimes. The delay-time differences between adjacent receivers are estimated using only the traveltime differences between adjacent receivers in the common shot gather. Independently, the delay-time differences between adjacent sources are estimated using only the traveltime differences between adjacent sources in the common receiver gather. Based on the delay-times or datum statics known at some stations the delay-times at all sources and receivers can be obtained. Thus, the any trade-off between the source and receiver delay-times can be removed. Moreover, the traveltime differences between adjacent traces are determined by their correlations, which avoid to trace the same refractor in order to pick the first arrivals from seismic data with low signal-to-noise. Test results of synthetic and real data show that relative delay-time method can overcome the problems that common delay-time method suffers, and has strong adaptability for the highly varying refractor velocity and rolling refactor surface.

refraction wave; relative delay-time method; delay-time method; statics; near-surface

国家自然科学基金项目(41074077, 41230318)；中国海洋大学“国家级大学生创新创业训练计划”项目资助。 Supported by the National Natural Science Foundation of China(41074077, 41230318)；the Program of “Nathonal Undergraduate Training Programs for Innoration and Entrepreneurship” of Ocean University of China

2015-08-22;

2015-11-20

杨华臣(1993-),男，硕士生。

** 通讯作者： E-mail:zhangjz@ouc.edu.cn

P631

A

1672-5174(2017)03-087-08

10.16441/j.cnki.hdxb.20150295

杨华臣， 康佳语， 张建中. 地震静校正的相对时延法[J]. 中国海洋大学学报(自然科学版), 2017, 47(3): 87-94.

YANG Hua-Chen, KANG Jia-Yu, ZHANG Jian-Zhong. The Relative Delay-Time Method for Seismic Statics[J]. Periodical of Ocean University of China, 2016, 47(3): 87-94.