土体修正剑桥模型p′:q:υ关系的归一化分析*
2017-03-11邓英军安振东杨俊杰
邓英军, 安振东, 杨俊杰
(1.中国石油工程建设公司华东设计分公司,山东 青岛 266071; 2.青岛双瑞海洋环境工程股份有限公司,山东 青岛 266101; 3.中国海洋大学环境科学与工程学院,山东 青岛 266100)
土体修正剑桥模型p′:q:υ关系的归一化分析*
邓英军1, 安振东2, 杨俊杰3❋❋
(1.中国石油工程建设公司华东设计分公司,山东 青岛 266071; 2.青岛双瑞海洋环境工程股份有限公司,山东 青岛 266101; 3.中国海洋大学环境科学与工程学院,山东 青岛 266100)
修正剑桥模型是基于临界状态理论下提出的一种描述黏土体应力-应变行为的弹塑性本构模型,具有形式简单、参数少并具有明确的物理意义,易采用试验确定,能够比较准确的描述黏土的应力-应变行为等优点。修正剑桥模型在描述土体力学行为时,需要表达土体有效应力p′,剪切力q和体积比υ的三者关系,这就要求将3个变量呈现在1个三维图表或者2个二维图表上。本文采用两种方法对模型中的3个变量进行归一化处理,通过对修正剑桥模型的屈服面方程进一步的推导和转化,将三者之间的关系用1个二维图形表示出来。与此同时,通过编写程序模拟土体三轴排水和不排水试验中的应力路径并将结果表现在二维图形中,发现模拟结果与常规方法一致,从而验证了该归一化处理的有效性和准确性。
修正剑桥模型;归一化;三轴排水试验;三轴不排水试验
英国剑桥大学Roscoe和他的同事[1-2]在正常固结黏土和超固结黏土试样的排水和不排水三轴试验的基础上,发展了Rendulic提出的饱和黏土有效应力和孔隙比成唯一关系的概念,提出完全状态边界面的思想。他们假定土体是加工硬化材料,服从Drucker公设[3]和相关联流动规则,根据能量方程,建立剑桥模型(Cam-clay Model)。由于剑桥模型假设中的简化,在应力比较小时计算得到的剪应变计算值一般都偏大,1968年Roscoe等[4]又进一步对剑桥模型做了修正,将关于塑性能的假定进行了修改,得到了著名的修正剑桥模型。这个模型采用帽子屈服面,相适应的流动法则和以塑性体应变为硬化参数。它在国际上被广泛的接受和应用,由于模型是基于土体的临界状态理论而提出的,因此也被称为临界状态模型。临界状态是指土体受剪切作用,在破坏时具有唯一的最终状态,无论是在排水还是在不排水条件下最后都会到达这种状态。具体定义为土体在剪切试验的大变形阶段,它趋向于最后的临界状态,即体积和应力(总应力和孔隙压力)不变,而剪应变还处于不断持续的发展和流动的状态[5-7]。临界状态线与试验的正常固结状态到临界状态的应力路径没有关系;有效应力路径终点都在同一条直线上—破坏线。
作为现代土力学开端的标志,剑桥模型是第一个真正意义上的土体弹塑性本构模型。因为具有形式相对简单、参数不多且有明确的物理意义和易于用简单试验所确定且能反映土变形的基本主要特性等优点,剑桥模型在当前土体本构模型研究过程中应用最为广泛,并已经积累了较多的应用经验,也在一些商用程序中被广泛使用。另一方面,人们也针对某些工程领域的特殊条件和需要建立有特殊性的土的本构模型,例如土的结构性模型[8]、损伤模型、UH模型[9-10]、各向异性模型[11]以及描述循环荷载条件下土的本构特性,如多重屈服面模型[12-13]、边界面模型等[14]。这些模型的建立大多数都是基于剑桥模型这个经典弹塑性模型基础之上的。其中,姚仰平提出的UH模型是在修正剑桥模型的基础上,通过引入统一硬化(unified hardening,UH)参数建立的,该本构模型能够反映饱和超固结土的剪缩、剪胀、硬化、软化和应力路径相关性等特性,模型所用土性参数与修正剑桥模型完全相同[15-16]。
本文结合前人关于剑桥模型的推导和论述,采用归一化方法,将有单位的变量进行无量纲化,通过对修正剑桥模型屈服面方程做进一步的推导和转化,将剑桥模型在三维图形中表示的三轴排水和不排水试验反映在二维图形中。
1 修正剑桥模型
剑桥模型属于弹塑性硬化本构模型范畴,单位体积土体受力所做的功由两部分组成,即弹性功增量dWe和塑性功增量dWp。弹性功增量表示为:
(1)
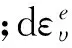
(2)
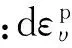
(3)
式中M为摩擦系数,其计算公式为:
(4)
上式中φ为土体的内摩擦角,根据式(2)和(3)可得:
(5)
由相关联性流动法则,即正交法则可以得到:
(6)
式中:dp′为平均有效应力增量;dq为剪切应力增量。由式(5)和(6)可得:
(7)
解此微分方程并利用q=0时p=p0的条件,可得:
剑桥模型屈服面方程:
(8)
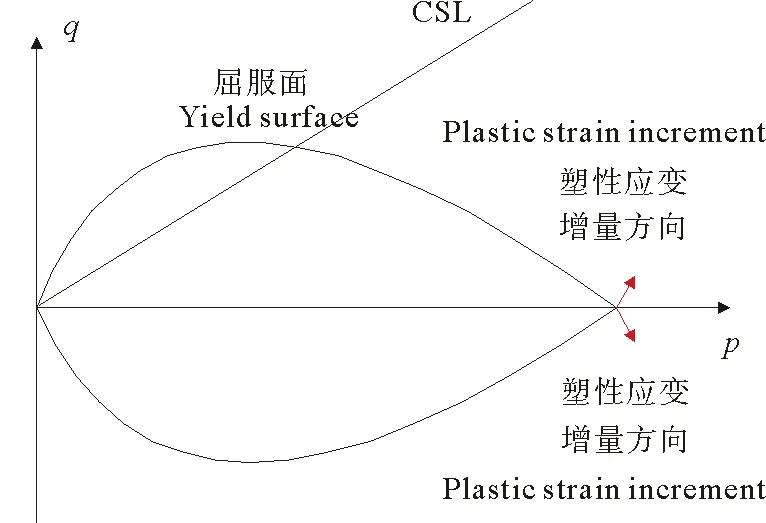
图1 原始剑桥模型屈服面[17]Fig.1 The yield surface of Cam-clay model[17]
由于在q=0时,原始剑桥模型屈服面存在一个奇异点(见图1),其外法线方向不确定,即塑性应变方向不确定,从而为数值计算带来困难。为了克服这两个问题,1968年Roscoe和Burland对剑桥模型做了修正,得到了著名的修正剑桥模型。主要修改了塑性功假设,既考虑体积应力产生的塑性功又考虑剪切应力产生的塑性功,将式(5)变为:
(9)
将式(9)化简得:
(10)
上式中η为应力比,其值为η=q/p′。采用与原始剑桥模型同样的推导方式,可得
(11)
上式为修正剑桥模型的屈服面方程,屈服轨迹为椭圆曲线,如图2所示。
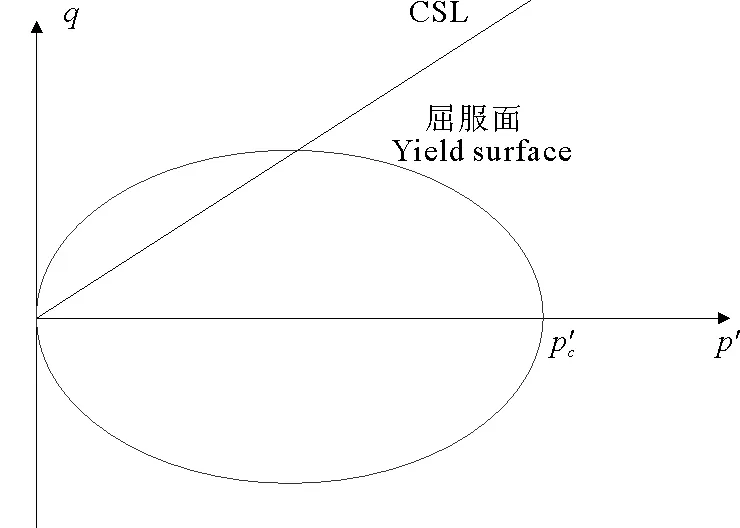
图2 修正剑桥模型屈服面

2 υλ-η坐标平面内的归一化分析
剑桥模型屈服面方程(11)可转化为如下形式:
(12)
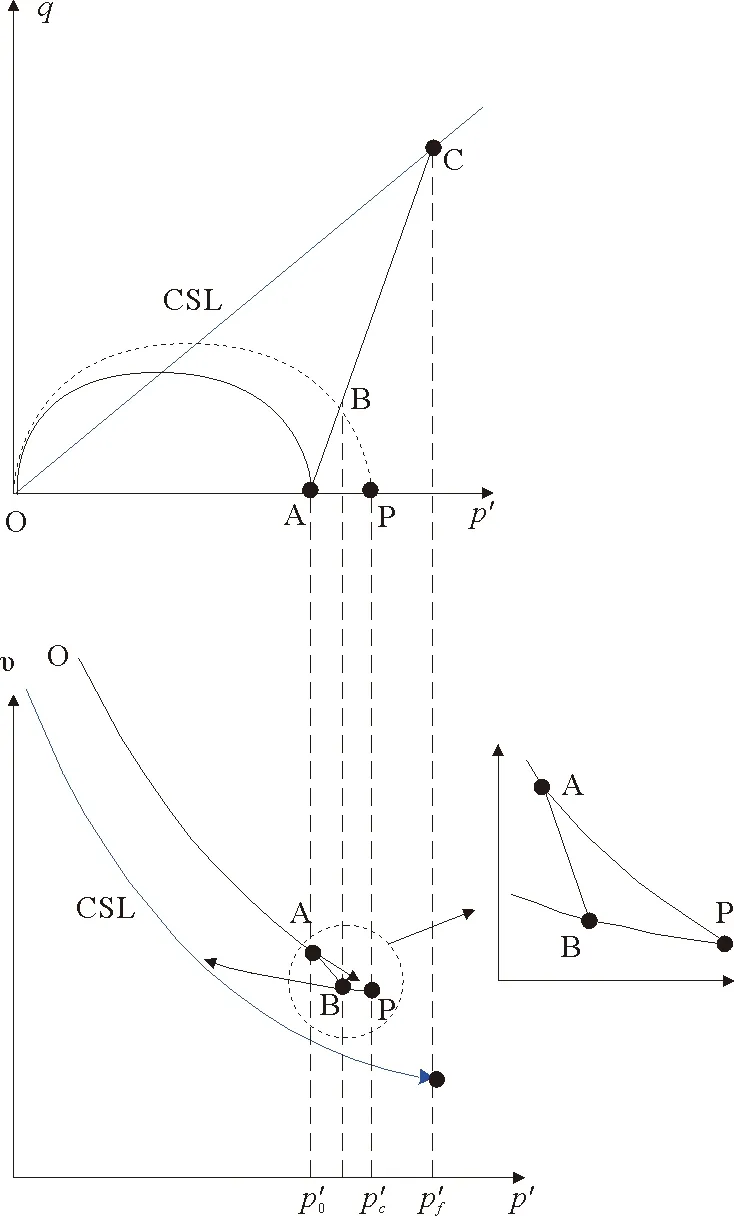
图3 修正剑桥模型对正常固结土三轴排水试验的分析结果
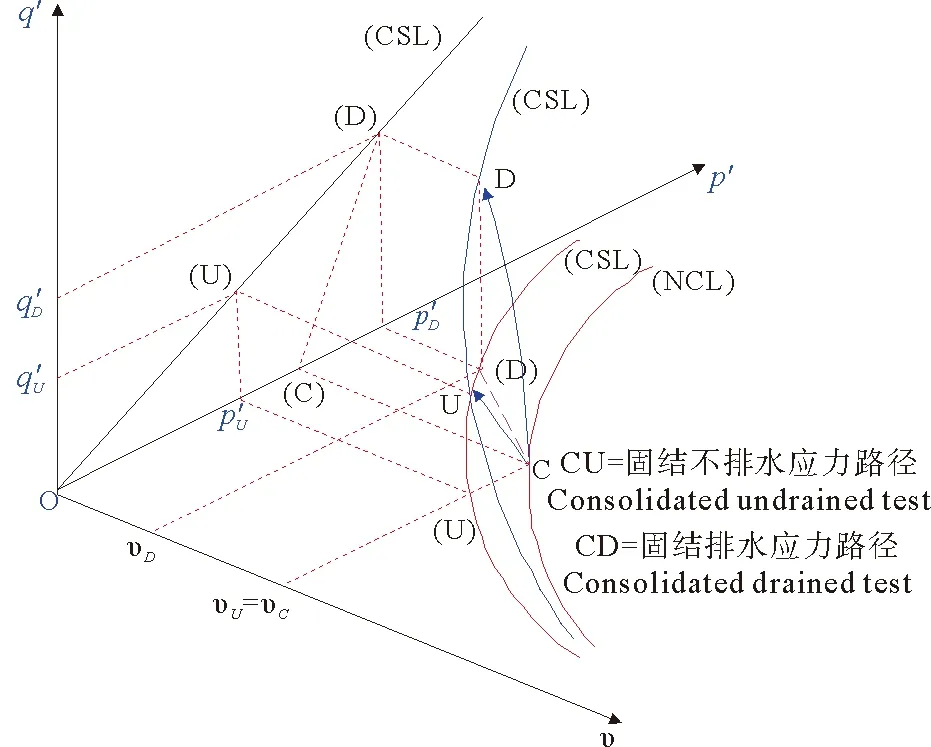
图4 修正剑桥模型的p′:q:υ三维空间
表示这一系列直线的数学表达式具有相同的形式,其数学表达式可写为如下形式:
υ=υλ-λlnp′。
(13)
将土体体积比υ和应力状态p′转化为求变量υλ形式:
υλ=υ+λlnp′。
(14)
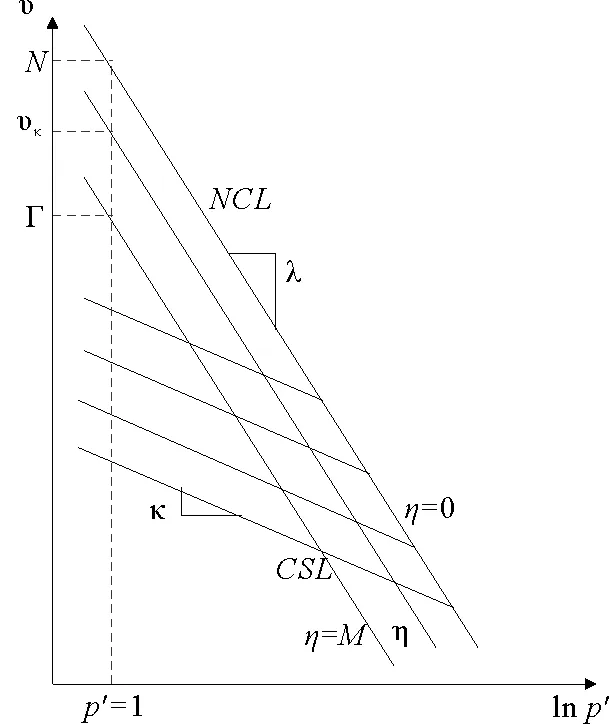
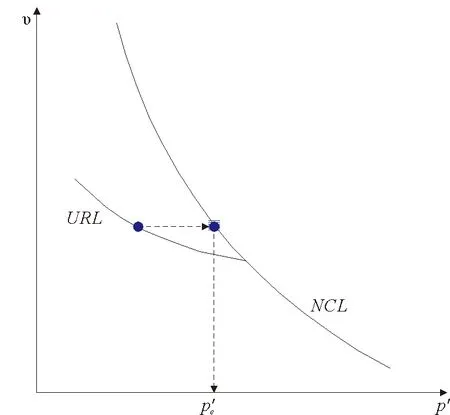
图5 υ-lnp′坐标平面内的正常固结线、临界状态线和回弹曲线
式中υλ为代表不同η值的直线在lnp′=0(p′=1 kPa)上的截距。其中对于正常固结线(NCL),即图5中的N值代表点的数学表达式:
η=0,υλ=N。
(15)
临界状态线(CSL),图6中K点对应的数学方程式为:
η=M,υλ=Γ。
(16)
根据图5中的NCL和卸载曲线,可推导得到土体体积比υ的表达式为:
(17)
根据式(14)和(17)得到:
(18)
由式(12)和(18):
随着峨眉武术的变迁,峨眉武术越来越泛化,微观意义上指以发源于峨眉山,并与巴蜀地域文化长期互动交融而形成的拳种流派。宏观意义上的理解更接近巴蜀武术的概念,不仅包括早期传入四川地域并与其地域文化互相适应,且己具有显著巴蜀地方文化特色的外来武术拳种,还包括从四川传播到其他地区以外的武术技术。
(19)
假定某确定的λ、N、M和κ的值,具体参数取值如表1所示。根据式(18)和(19)编写程序,得到剑桥模型中η-υλ的关系曲线(见图6)。图中的NYZ可以理解为剑桥模型的屈服轨迹在二维图形中的体现。
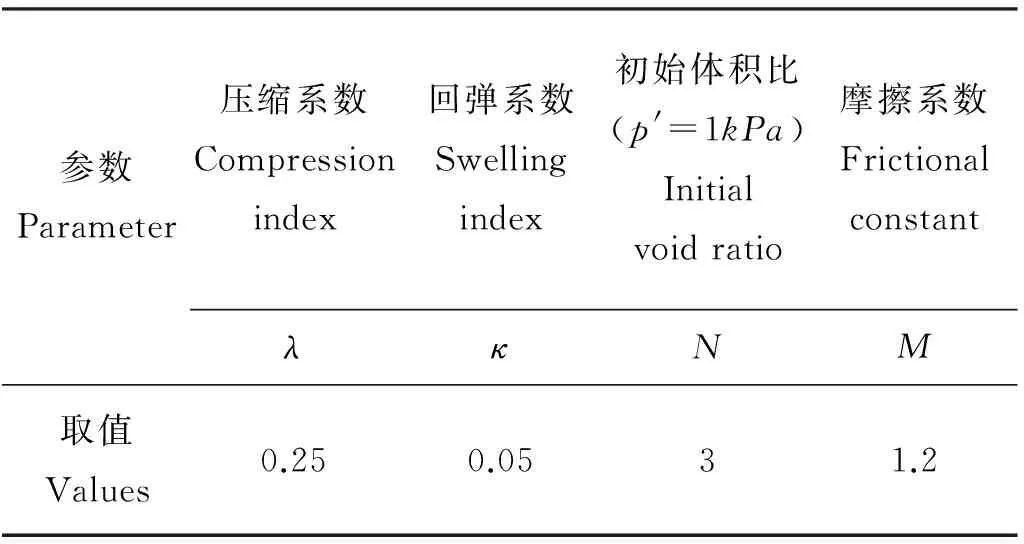
表1 土体三轴试验模拟参数
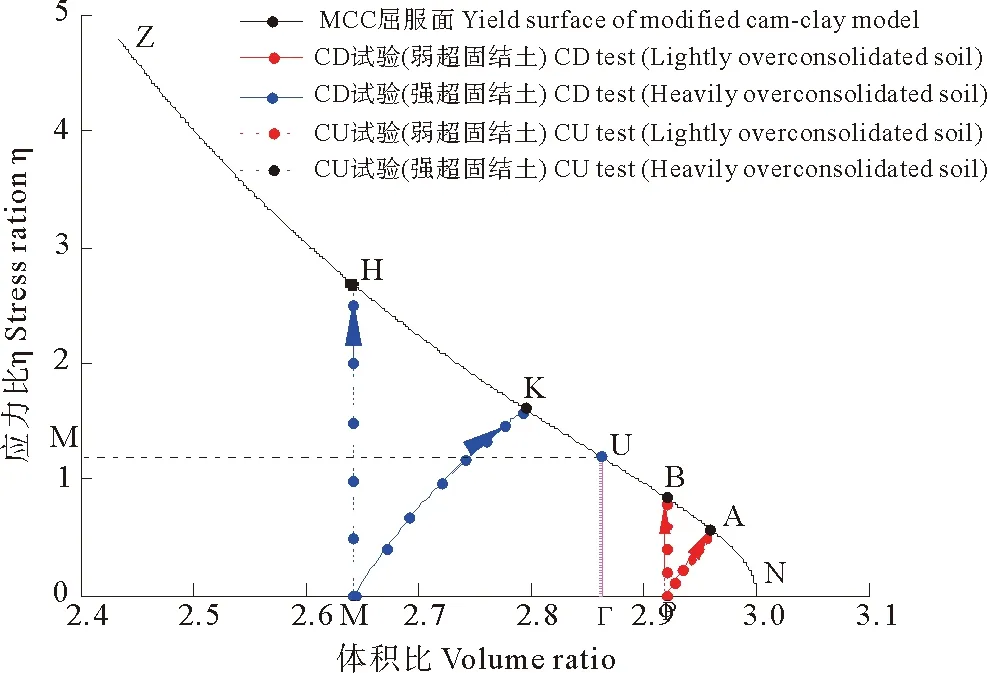
图6 υλ-η坐标平面内三轴排水试验和不排水试验的应力路径
对于正常固结土而言,等向固结压缩试验的排水路径和不排水路径都是在N点出发,延曲线NY到达临界状态点Y。
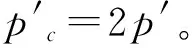
与此同时,轻超固结土(1
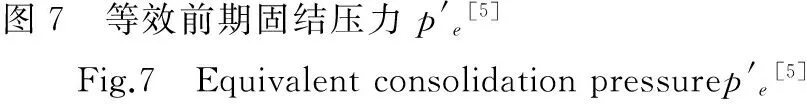
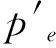
υ=N-λlnp′。
(20)
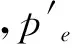
(21)
由式(18)和(22)得到如下表达式:
(22)
其中α表达式为:
(23)
由式(22)和屈服面方程(12)可得:
(24)
根据应力比η=q/p′,很容易得到:
(25)


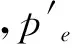


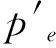
3 结语
本文提出的两种归一化方法,在二维坐标范围内将土体的三维p′:q:υ特性信息表示出来。并且能够在一张二维坐标中详细的表示土体的排水和不排水三轴应力行为,图形简单、信息量丰富。与此同时,通过编写程序模拟土体三轴排水和不排水试验中的应力路径并将结果表现在二维图形中,发现模拟结果与常规方法一致,从而验证了该归一化处理的有效性和准确性。另外,本文所提出的两种无量纲方法证明:基于土体有效应力来反映土体的行为,不同的试验方法只是单一解释了土体行为的不同方面。
[1] Roscoe K H, Schofield A N, Wroth C P. On the yielding of soils[J]. Geotechnique, 1958, 8(1): 22-53.
[2] Roscoe K H, Schofield A N, Thurairajah A. Yielding of clays in states wetter than critical[J]. Geotechnique, 1963, 13(3): 21-40.
[3] 龚晓南编著. 土塑性力学[M]. 杭州: 浙江大学出版社. 1997. Gong Xiao-Nan. Soil Plastic Mechanics[M]. Hangzhou: Zhejiang University Press, 1997.
[4] Roscoe K H, Burland J B. On the generalised stress-strain behaviour of wet clay[J]. Engineering Plasticity, 1968: 535-609.
[5] Wood D M. Soil Behaviour and Critical State Soil Mechanics[M]. Cambridge: Cambridge University Press, 1990.
[6] Schofield A N, Wroth C P. Critical State Soil Mechanics[M]. London: Mc Graw-Hill, 1968.
[7] 罗汀. 土的本构关系[M]. 北京: 人民交通出版社, 2010. Luo Ting. Soil Constitutive Models[M]. Beijing: China Communications Press, 2010.
[8] Liu M D, Carter J P. A structured cam clay model[J]. Canadian Geotechnical Journal, 2002, 39(6): 1313-1332.
[9] 姚仰平, 侯伟, 罗汀. 土的统一硬化模型[J]. 岩石力学与工程学报, 2009, 28(10): 2135-2151. Yao Yang-Ping, Hou Wei, Luo Ting. Unified hardening model for soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(10): 2135-2151.
[10] 姚仰平. 土的统一硬化模型及其发展[J]. 工业建筑, 2008, 38(8): 1-56. Yao Yang-Ping. Unified hardening model for soils and itsdevelopment[J]. Industrial Construction, 2008, 38(8): 1-56.
[11] Wheeler S J, Karstunen M. An anisotropic elastoplastic model for soft clays[J]. Canadian Geotechnical Journal, 2003, 40(2): 403-418.
[12] Mroz Z, Norris V A, Zienkiewicz O C. An anisotropic, critical state model for soils subject to cyclic loading[J]. Geotechnique, 1981, 31(4): 451-469.
[13] Mroz Z, Norris V A. Elastoplastic and Viscoplastic Constitutive Models for Soils with Application to Cyclic Loading[M].Soil Mechanics-Transient and Cyclic Loads. New York: Wiley, 1982: 173-217.
[14] Dafalias Y F, Herrmann L R. Bounding Surface Formulation of Soil Plasticity[M]. Soil Mechanics-Transient and Cyclic Loads. New York: John Wiley& Sons Ltd.1982, 10: 253-282.
[15] 姚仰平, 侯伟. 土的基本力学特性及其弹塑性描述[J]. 岩土力学, 2009, 30(10): 2881-2902. Yao Yang-Ping, Hou Wei. Basic mechanical behavior of soils and theirelastoplasticmodeling[J]. Rock and Soil Mechanics, 2009, 30(10): 2881-2902.
[16] 姚仰平. UH模型系列研究[J]. 岩土工程学报, 2015, 37(2): 193-217. Yao Yang-Ping. Advanced UH models for soils [J]. Chinese Journal of Geotechnical Engineering, 2015, 37(2): 193-217.
[17] 刘明. 饱和软黏土动力本构模型研究与地铁隧道长期振陷分析[D]. 上海: 同济大学, 2006. Liu Ming. Saturated Soft Clay Dynamic Constitutive Model Research and Long-Term Tunnel Vibration Settlement Analysis [D]. Shanghai: Tongji University, 2006.
责任编辑 庞 旻
Two-Dimensional Representations ofp′:q:υInformation in Modified Cam-Clay Model
DENG Ying-Jun1, AN Zhen-Dong2, YANG Jun-Jie3
(1.CPECC East China Design Branch, Qingdao 266071, China; 2.Sunrui Marine Environment Engineering Co., Ltd, Qingdao 266101, China; 3.College of Environmental Science and Engineering, Ocean University of China, Qingdao 266100, China)
The Modified Cam-claymodel is aelasto-plastic constitutive model which is used to describe the stress-strain behavior of soils. The model is simple because it was defined only by five parameters. It was established based on the critical state theory and can describe the behavior of clay more accurately. In addition, the parameters in themodel which can bedetermined easily by indoor soil tests have clear physical meanings. The relationship of the mean effective stressp′, the deviator stressqand specific volumeυwas usually used to describe the soils mechanical properties in the model. As a result, a three-dimensional figureor two two-dimensional ones which reflect the relationship between two variablesrespectively are needed. In this paper, the three variables in Modified Cam-claymodel were normalized using two different methods. Two-dimensional graphs which can reflectsp′:q:υrelationship were drawn respectively after further derivation and transformationof the model yield surface equation. At the same time, the stress paths of soil triaxial drained testand triaxialundrained test were simulated by programing and the results were drawn in two-dimensional figure. It is found that the stress path resultsconsistent with that obtained using the usual methods. Finally, the accuracy and rationality of the normalization methodsare confirmed.
Modified Cam-clay model; normalization; drained triaxial tests; undrainedtriaxial tests
国家自然科学基金项目(50779652)资助 Supported by the National Natural Science Foundation of China (50779652)
2015-11-25;
2016-07-17
邓英军(1989-),男,硕士,工程师,主要从事岩土及地下工程设计和研究方面的工作。E-mail:dengyingjun@cnpccei.cn
** 通讯作者:E-mail: jjyang@ouc.edu.cn
TU443
A
1672-5174(2017)03-095-06
10.16441/j.cnki.hdxb.20150401
邓英军, 安振东, 杨俊杰. 土体修正剑桥模型p′:q:υ关系的归一化分析[J]. 中国海洋大学学报(自然科学版), 2017, 47(3): 95-100.
DENG Ying-Jun, AN Zhen-Dong, YANG Jun-Jie. Two-dimensional representations ofp′:q:υinformation in modified cam-clay model[J]. Periodical of Ocean University of China, 2017, 47(3): 95-100.
