面对上网“搜题”，我们该怎么办——从一道相似综合题的“网传解答”说起

☉浙江绍兴市新昌县七星中学 甄亚芳

面对上网“搜题”，我们该怎么办
——从一道相似综合题的“网传解答”说起

☉浙江绍兴市新昌县七星中学 甄亚芳

最近一次家庭作业中我们选用一道以矩形为载体的综合题，该题的后两问较复杂，从批改作业情况来看，几个学生使用了搜题软件，出现了与网上错漏相同的解答，作为一次“反面”教育资源，笔者将相关解答呈现给学生，然后大家一起纠错，使得同学们对该题的理解走向深刻.本文记录这次解题教学的过程，并跟进教学思考，供研讨.

一、相似综合题的“网传解答”与评析

考题：如图1，在矩形ABCD中，AB=m，BC=4，点M为边BC的中点，点P为边CD上的动点（点P异于C、D两点）.连接PM，过点P作PM的垂线与射线DA相交于点E.设CP= x，DE=y.

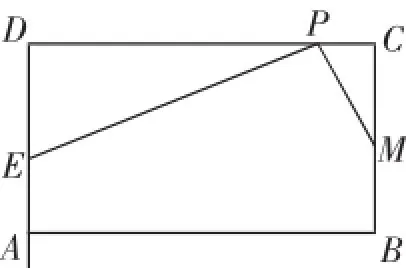
图1

（1）求y与x之间的函数关系式.

（2）若点P在线段DC上运动时，点E总在线段AD上，求m的取值范围.

（3）当m=8时，是否存在点P，使得点D关于直线PE的对称点F落在边AB上？若存在，求x的值；若不存在，请说明理由.

某网站上的解答：

（1）求解并不复杂，限于篇幅这里只给出简要思路.由“一线三等角”易证△PCM∽△EDP，可得比例式代入参数运算出

评析与纠错：看到少数学生写了这样的解答，初看感到莫名其妙，后来渐渐想通他们出错的原因，原来是利用了关于x的二次函数的最值公式，列出这个最值不大于4的不等式，但这是一个关于m的二次不等式，变形时把不等号弄错成“≥”，使得后面解这个二次不等式也出现错误.

（3）存在，过点P作PH⊥AB于H点.

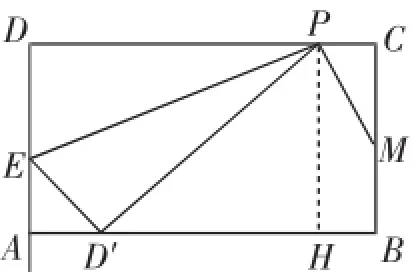
图2

在Rt△D′PH中，PH=4，D′P=DP=8-x，根据勾股定理，得

因为∠ED′A=180°-90°-∠PD′H=90°-∠PD′H=∠D′PH，∠EAD′=∠PHD′=90°，所以△ED′A∽△D′PH，整理得

评析与纠错：上述解法只有个别学生“抄”在解答处.追问他们如何理解的，也吱唔着说不清楚，几个优秀学生更是对“”表示不会化简、整理.而且还有优秀学生指出“＞4”并一定要舍去，因为第（3）问中没有强调点E一定要在边AD上！

我们可以增设AD′=a，则BH=x，D′H=8-a-x，PD′= PD=8-x，D′E=DE=y，由△AD′E∽△HPD′，可得比例式可得a=2x，回代比例式，得.其中图2对应着的情况，而被“网传答案”舍去的那种情形也可直观构图如下，见图3.

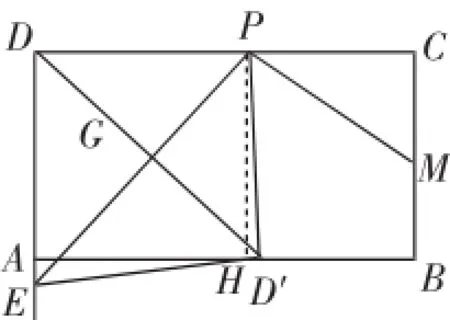
图3

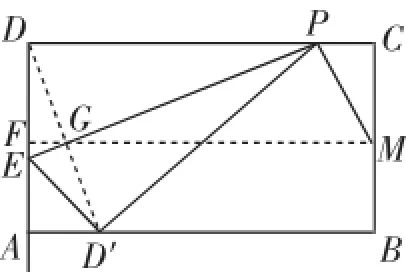
图4

课堂片断记录：上述演算之后，虽然能贯通思路，算法也相较“网传答案”简化一些，但仍然不是很简洁的运算.后来班级上有优秀学生提出还可以创造条件、构造“射影定理”基本图形，简化运算.如图4，设DD′交折痕PE于G，作直线GM交AD于F点，根据折叠性质、对称性质、平行线等分线段定理，有F为DA的中点，则有△DFG≌△MCP，所以FG=x，于是在Rt△GDE中，符合射影定理基本图形，有FG2=DF·EF，可列出方程x2=2（y-2），把4x代入可转化为关于x的方程，从而求出答案.

二、关于解题教学的进一步思考

1.搜题软件、网站泛滥，如何引导学生正确使用是关键.

近几年来，由于信息技术、网络的普及与带速的提升，特别是智能手机的普及，各大题库平台、搜题软件泛滥，学生可以轻松使用检索、拍题方式获得相关试题的解答或答案.然而“天下没有免费的午餐”，这些免费的解答往往也存在不同的问题，有些甚至是错漏解答，如果学生不加鉴别而直接“复制”，或习惯于遇到困难就上网找答案，则对数学学习无甚益处.所以我们认为如何正确引导学生上网检索答案，获取帮助是当前面临的一个急迫课题.如果面对一道较难习题，缺少思路或解题念头，求助老师又不方便，可以在家长的监督下搜索，但重要的是如何理解网上的答案，并对错误解法大胆质疑、究错，而不是不求甚解，甚至直接抄到作业中应付老师检查.

2.对问题结构的深刻理解可使繁杂解法走向简化表达.

我们知道，数学上“算法简单的方法往往要付出逻辑思维的代价”.在求解上面考题的第（3）问时，我们就感受到这点，“网传解答”思维量不大，只要依次代入列出方程，只是这个繁杂的方程让很多学生望而却步，难以进展下去.我们优化这种关系之后，使得方程稍稍简化，但仍然需要一定的运算量；而引导学生讨论后，有学生提出了更为简化的解法，但是却需要对问题的深层结构有深入的理解，并且需要构造和认识射影定理的基本图形，对数学思维有较高的要求.

3.在难点破解上引导学生参与研讨，往往能生成精彩.

在讲评这道考题时，笔者没有深入预设到学生最后提出的更为简化的解法，而是在安排学生讨论解法和理解思路时得到精彩生成，对该图形结构的精准理解构造出了射影定理的基本图形，使得一个简洁的一元二次方程得以出现，节约了运算的时间.可能课堂教学中，适时在难点破解进程中，引导学生参与研讨，往往有意外的收获.

4.变式改编，跟进检测，反馈解题教学效果.

为了追求较好的讲评效果，我们还对考题进行了变式改编，供学生练习巩固，可有效反馈学生的理解程度.作为本文最后，我们附上该题的变式改编.

变式改编题：如图5，在矩形ABCD中，AB=m，BC=4，点M为边BC的中点，点P为边CD上的动点（点P异于C、D两点）.连接PM，过点P作PM的垂线与射线DA相交于点E.设CP=x，DE=y.

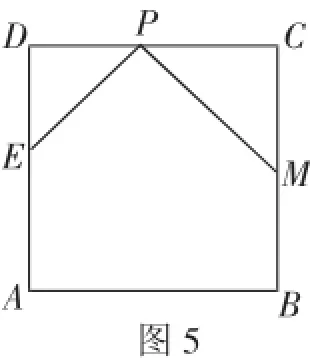
图5

（1）当m=4，x=2时，求y的值；

（2）当m=4时，求y与x之间的函数关系式；

（3）若点P在线段DC上运动时，点E总在线段AD上，求m的最大值；

（4）当m=8时，将矩形一角∠D沿直线PE翻折，当点D恰落在边AB上时，求x的值.

三、写在后面

《人民教育》近期有一篇文章提到“数学是一个深层次的人文活动，并指出，数学不是简单的教给学生知识或进行技能训练，而是要在解决问题中激发学生对学习的热爱及社会责任感.”我们以为，对于网络搜题这一不可阻挡的流行方式，一味地堵是不可能的，只有想法疏导，通过引入一些网站上的典型错漏解法，引导学生参与思辨，并深化认识，使得他们科学、全面、准确地看待这些资源或素材，这样可逐步培养学生的批判精神和科学求真品质.

1.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

2.罗增儒.巧在本质关系的提示妙在深层结构的接近（上）［J］.中等数学，2007（3）.

3.鲍建生，顾冷沅等.变式教学研究［J］.数学教学，2003（1、2、3）.

4.许燕.从解题赏析走向教学研究——以2016年无锡卷第27题为例［J］.中学数学（下），2016（10）.