从数学史知识中汲取历史智慧

☉福建厦门大学附属实验中学

☉杨跃鸣名师工作室林运来

从数学史知识中汲取历史智慧

☉福建厦门大学附属实验中学

☉杨跃鸣名师工作室林运来

习近平同志指出：“历史是最好的教科书.”数学史是一座宝藏，不论时代如何变迁，从事数学研究和数学教育的人总是可以并且也有必要从中汲取丰富的教学素材和有益的思想养料，为教学注入鲜活的生命力.但是，数学史的应用历来是“高评价，低应用”.当前的数学教学，多数教师还只是把数学史作为一种“附加”的内容，把数学史作为一种提高学生兴趣的“佐料”，没有从数学历史发展的角度设计自己的教学，无法充分挖掘数学史的教育价值和文化价值.导致这一现象的一个重要原因就是教师的数学史素养不足、数学史素材极为匮乏.有的教师连基本的数学史知识都没有，更遑论在课堂上主动、自觉、恰当地融入数学史知识，激发学生学习动力，增强学生学习数学的情感，启迪学生的数学思维了.

数学令那么多人着迷，原因在哪里？教学中如何选择符合学生接受水平的数学史知识？如何通过数学史实介绍数学的思想方法？“科学给人知识，历史给人智慧”.数学教育不可能完全割裂历史，数学史和数学教学结合已是国际数学改革的一种趋势.教师多读一读数学史书籍，研究好、利用好有关的数学史知识，有助于找寻到上述问题的答案.在对数学史的深入思考中，理解数学、提升专业素养、把握当下、走向未来具有重要现实意义.笔者谈谈阅读《数学史上的里程碑》［1］的体会与启示，期望起到抛砖引玉的作用.

一、数学史知识对教师的意义

1.数学史知识有助于提高教师理解数学的水平.

“理解数学、理解学生、理解教学”是教师专业发展的基石，是数学教学质量的根本保证，其中“理解数学”是首要的，是实现数学育人的根基［2］.教材是学生获取知识的主渠道.随着学习的深入，知识积累的增多，基本数学思想和数学方法在知识形成的过程中发展，数学能力在知识、方法和技能的学习过程中提高，这是教材的一个重要效应.教材的导言、小结和阅读材料中有很多有益的启示，教师要“志业地读懂教材”，在教学中发挥这些素材的重要效应.

案例1：一元二次方程的教学.

人教版教科书在一元二次方程的引入及求解时，都是以与面积有关的实际问题作为背景材料的.北师大版教材则是在学习配方法解一元二次方程这节内容后，通过设置“读一读”栏目——“一元二次方程的几何解法”，介绍我国三国时期的数学家赵爽和公元9世纪阿拉伯数学家花拉子米利用几何方法求解一元二次方程的例子.如何理解教材的编写意图，把握这一主题的实质？

事实上，在数学发展的早期，几何先于代数发展起来，人们习惯从几何的角度思考代数问题.古希腊的毕达哥拉斯学派曾经用几何方法解二次方程.在古希腊，几何学发展得快而代数学发展得慢.当时，一元二次方程被分为四种不同的类型：x2-px+q2=0，x2+px+q2=0，x2-px-q2=0和x2+px-q2=0，并且远没有今天这样的符号［3］.公元9世纪，花拉子米用几何方法解一元二次方程，并给出了一元二次方程的两种几何解释.其要点是把未知数的平方视为正方形的面积，未知数与常数的积视为两个矩形的面积之和，然后以这三个图形为基础，补形成正方形，从而得到原方程的解［4］.这样的解法很容易弄懂，但是为什么要用这样复杂的方法（几何作图法）去处理这么简单的问题（一元二次方程），却颇令人费解.事实上，补形成正方形是从几何角度说的，从代数的角度而言，配方的目的就是为了达到补形的效果［4］.知道了这一历史发展和背景知识之后，有助于我们理解教材的选材和立意，并从中获得很多有益的启迪，不会因几何法落后而把其精神实质给抛弃了.

笔者所在地区使用的是北师大版教材，教学配方法之后，为使学生能“历史地”看问题，我布置了下面的思考题（改编自文献1）.

例1（Ⅰ）设r和s表示下列方程的两个根：x2-px+q2= 0，其中p和q是正整数，试证明：r+s=p，rs=q2，且当时，r和s都是正数.

（Ⅱ）为了用几何方法解（Ⅰ）中的二次方程得到实根，我们必须由给定的线段p和q求出线段r和s.也就是说，我们必须作一个长方形，使它的面积等于一个给定的正方形的面积，而它的长与宽之和等于一个给定的线段.试根据图1，设计一个适当的作图方案，并且在几何上证明：为了能得到两个实根，我们必须有

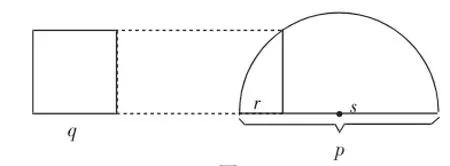
图1

（Ⅲ）给定一个单位线段，试用几何法解二次方程x2-7x+12=0.

补充这个问题，基于以下原因.一是让学生增添新的视角看一元二次方程的求解，而且在学习勾股定理、平方差公式、完全平方公式等内容时，学生已经具备通过构造图形解决问题的数学经验；二是让学生体会并走一走古代数学家走过的路，进一步从形象化的角度理解配方法，在几何法与代数法的比较中认识到用代数方法研究几何问题是必然的历史选择；三是可以进一步引导学生发现韦达定理.

这样的教学不拘泥于数学知识的历史顺序，而是通过抽象思维与形象思维的结合，使学生从形与数的结合上深刻认识数学的本质，进一步感受代数方法的优越性，在数学历史文化与数学思维的双重熏陶下，有利于学生数学素养的提高，同时必然促进学生数学能力的发展，进而发挥教材的多种效应.

2.数学史知识有助于提高教师教学的创新能力.

通过数学历史的演变，回眸数学发展中的重要事件和人物，有助于认识数学观念上的关键转折点，也就是人们常说的“里程碑”，这为我们有层次地在不同学段有选择地安排不同内容提供了重要的参考.

案例2：勾股定理的教学.

勾股定理可谓初等几何中最精彩、最著名和最有用的定理之一，它从边的角度进一步刻画直角三角形的特征.学习勾股定理及其逆定理是进一步认识和理解直角三角形的需要，也是后继有关几何度量运算和代数学习的必要基础.勾股定理有各种推广，自然的引申就是一般三角形的余弦定理和平面解析几何中的两点间距离公式.教学中，笔者把余弦定理的证明留给学生作为练习.

例2证明：在一个三角形中，与钝角（锐角）相对的边上的正方形，等于其他两边上的正方形之和，加上（减去）这两边中任何一边与另一边在它上面的投影之积的二倍.

笔者首先引导学生结合勾股定理的形式，从证明的结论看，应通过构造直角三角形进行证明.问题解答后，笔者进一步指出，如果采用有向线段，在图2中，有：

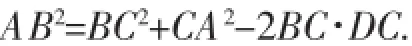
因为DC=CA·cos∠BCA，所以AB2=BC2+CA2-2BC· CAcos∠BCA，其实质就是余弦定理.

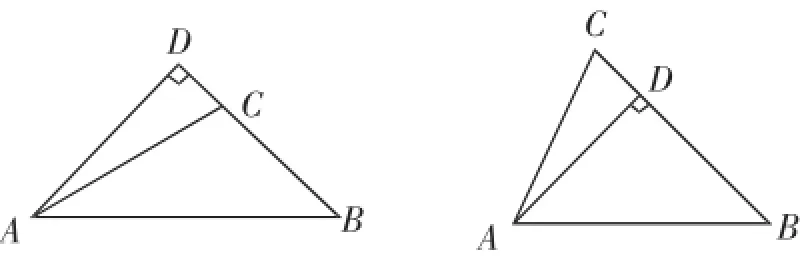
图2

教学中进行这样的“创新”设计，能让学生体会到数学知识和数学公式的内在美和形式美，有助于沟通初高中知识的联系，使学生认识到勾股定理具有学科的基础性和广泛的应用，余弦定理不过是勾股定理的一个很好的推广.

案例3：有理数乘方的教学.

教学有理数的乘方后，笔者引导学生对所学知识进行总结，同时指出，加法与乘法表面上是极不相同的运算，但在结构上却有相似之处.若从1出发，不断加1，得到序列1，2，3，4，5，…；从2出发，不断乘2，也得到序列2，22，23，24，25，….

两个序列在运算关系上也相似，前一序列中有1+3= 4，后一序列中就有2×23=24，即2×8=16.认识到这一点，我们就可以不必直接计算2×8=16，而去计算1+3，得到4，然后就知道24=16是2×8的答案了.

由于同一结构可以在不同的事物中出现，但有的事物容易把握，有的事物很难把握，这样，我们可以通过容易把握的事物，来认识难以把握的事物［5］.在历史上，数学的一大历史成就就是利用这一思想，为了简化计算而发明了对数，一下子把天文学家从大量计算的沉重劳动中解放出来了.

这样的教学，有助于学生沟通数学各部分知识的内在联系，开阔学生的视野，让学生体会数学思想的重要意义.知识是一种改变历史的力量，但归根结底，知识的力量来自人的思想.正如日本数学教育家米山国藏所言：“无论对于科学的工作者、技术人员还是数学教育工作者，最重要的是数学精神、数学思想和方法，而数学知识是第二位的.”

3.数学史知识有助于提高教师的解题研究能力.

“问题是数学的心脏”.数学学习的过程与数学解题紧密相关，但是很多人可能是通过题海战术而训练成解题能手的.数学能力的提高在于解题的质量而非解题的数量，因此重在研究解题的思维方法和策略，解题时要不断思考，这道题为什么要这样解？这样的解法是不是触及了数学的本质？背后还蕴藏了怎样的数学观点、数学思想方法？

图3

文献1给出如下的几何证法.

证明：即证明正方形的边和对角线是不可公度的.假设情况相反，那么就存在一个线段AP（如图3），使得正方形ABCD的对角线AC和边AB都是AP的整数倍，也就是说，AC和AB关于AP是可公度的.在AC上，截取CB1=AB，作CA的垂线B1C1.不难证明C1B= C1B1=AB1.于是AC1=AB-AB1和AB1关于AP是可公度的.但是，AC1和AB1是尺寸比原来的正方形的一半还要小的一个正方形的对角线和边.由此可知，重复上述过程足够多次，最后我们就能得到一个正方形，它的对角线ACn和边AB1关于AP是可公度的，并且ACn＜AP.这是矛盾的，原问题得证.

上述证明方法即归谬法.如果把几何语言转化为代数语言来表示，就会发现这与费马的无限递降法有异曲同工之妙，费马曾利用无限递降法作出许多重要的发现，他的一生为我们留下了许多重要的定理与猜想，为数学与自然科学的发展作出了重要的贡献.

德国哲学家叔本华说过：“记录在纸上的思想就好像沙上行走者的足迹，我们也许能看到他所走过的路径，但如果要知道他在路上究竟看到了什么，则必须用我们的眼睛.”像文献1，作者“不局限于历史，着眼于思考与创新”，在每一讲的最后，都精心设计了相关的习题，读者阅读和思考的过程，就是在领会数学家如何创造数学的基础上自己再创造数学的过程，有助于我们更好地回归知识的源头，获得对思想过程的重要认识，看到数学家在发明、发现中的经典方法，体会问题是数学发展的关键，促进解题能力有效提高.

二、结束语

数学应该是一个充满乐趣并令人感到兴奋的学科，教科书作为一种需要理解和解释的正式文本，需要教师抓住蕴藏在教材中的核心概念和思想方法，将数学知识的学术形态转化为利于学生理解的教育形态，培养学生的学科核心素养.数学教师教学水平的高低，首当其冲体现在对教学内容的把握上.高水平的教师，在教教材显性知识的同时，能挖掘出其背后的隐性知识，教一些别人教不出来的内容，这些不易教的隐性知识，就是数学的本质［6］.

数学历史文化中蕴含着丰富的课程资源［4］，利用数学史知识可以激发学生的学习兴趣，培养学生的数学精神，启发学生的人格成长，预见学生的认知发展，指导并丰富教师的课堂教学，促进学生对数学的理解和对数学价值的认识，构筑数学与人文之间的桥梁等［7］.作为数学教师，掌握一定的数学史知识，有助于深入体会和理解数学内容所反映的思想、精神，进一步打开视野，在教学中善于抓住数学的核心概念和思想方法，在传授知识的同时，揭示数学知识所蕴含的科学方法和理性思维过程，使课堂闪烁着思维的火花，促进学生学科素养的形成和提高.

1.H·伊夫斯著，欧阳绛等译.数学史上的里程碑［M］.北京：北京科学技术出版社，1990.

2.章建跃.理解数学是教好数学的前提［J］.数学通报，2015，54（1）.

3.欧阳绛.数学方法溯源［M］.大连：大连理工大学出版社，2008.

4.徐章韬，顾泠沅.面向教学的学科知识之课程资源开发——以数学学科为例［J］.教育发展研究，2014（12）.

5.张景中.数学与哲学［M］.大连：大连理工大学出版社，2008.

6.李祎.高水平数学教学到底该教什么［J］.数学教育学报，2014，23（6）.

7.汪晓勤.HPM的历史渊源［J］.数学教育学报，2003，12（3）.