例谈数形结合在概念教学中的应用

【摘要】小数是一个抽象的数学概念。教学时，教师可以采用数形结合的教学方式，巧妙地将抽象的数学概念与直观的图形结合起来，为学生提供感悟知识、理解概念的机会，帮助他们准确把握数学概念，建立知识结构。

【关键词】数形结合；概念教学；认识小数

【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009（2017）01-0057-02

【作者简介】黄红成，江苏省扬州市江都区实验小学（江苏扬州，225200）教导处副主任，一级教师，扬州市数学学科带头人。

儿童学习数学是有基础的，这些基础包括生活中积累的经验、学习中获得的知识和活动中形成的能力。数学教学应从他们的“最近发展区”出发展开教学，为实现和促进他们的数学理解而努力。但有时教材呈现的教学方法无法契合儿童对知识掌握的需求，致使教师教学时如蜻蜓点水般一带而过，学生对知识的理解浅尝辄止，难以准确地把握数学知识的本质和意义，难以实现对数学问题的深度理解。

元、角、分三种货币单位每相邻两个单位之间的进率正好是10，因而成为苏教版三下《认识小数》一课教学素材的首选。但是在运用人民币素材进行教学时，教材通常采用直接告诉的方式来让学生把握和感悟小数的意义，教学形式略显抽象和单一，而且教学之间缺乏必要的联系，无法让学生清晰而准确地把握小数的意义。因此，教师不妨采用数形结合的方式来进行教学。

一、借助圆形，准确感悟小数的意义

学生认识数学概念不是一蹴而就的，而是一个感知、感悟并逐步深入的过程，认识小数的意义也是如此。教材呈现的教学思路是让学生借助人民币的单位进率来感悟小数的意义和特征，把元与角的关系作为学生认识小数的基础，从而引出十分之几的分数。在教材的基础上，笔者引入“圆形”进行了如下教学。

出示一枚1元硬币的图形，淡化1元的背景图案，把1元平均分成10份。

师：从图中可以看出，1份表示多少钱？1角是其中的几份？是1元的几分之几？就是十分之几元？ 生：1份表示1角，1角是其中的1份，是1元的，是元。

师：元还可以写成0.1元。0.1是我们今天要认识的一个小数。

师（显示其中的两份）：2角是其中的几份？是几分之几元？还可以写成什么？

生：2角是其中的2份，是元，还可以写成0.2元。

师：按照这样的思路，从图中你还能想到哪些价钱？可以怎样写？

有了圆形作为分析和理解问题的支撑，学生能始终围绕图形来感悟小数与分数之间的关系。用一个圆来表示1元，看似信手拈来，实则别具匠心。这样教学，既巧妙地用圆形来代替人民币的计量单位“元”，又自然地从抽象的计量单位过渡到直观的图形。另外，借助圆形，在初步引导学生认识其中的1份和2份后，让他们自主选择其中的几份来认识小数，不仅能使教学显得生动、灵活，而且为学生提供了将感悟到的知识和方法外化的空间。

二、借助矩形，全面把握小数的内涵

单一的教学形式难以使学生全面地把握数学概念，教师可以运用变式来突出数学概念的内涵。人民币有硬币和纸币两种形式，硬币可以“直观”成圆形，而纸币可以“直观”成长方形。之前教师采用了“把元分成角”的思路展开教学，反过来也可以尝试“把角合成元”。如此教学，既变换了教学素材，又丰富了教学形式，从而帮助学生全面地认识小数。

出示10张1角纸币。

师：这些是1角纸币，多少角就是1元？10角是几分之几元？用小数怎样表示呢？

生：10角就是1元，是元，用1.0元来表示。

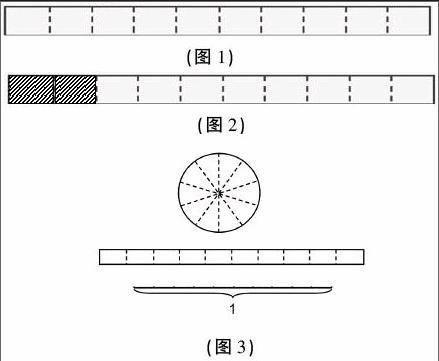
出示图1。

师：如果整个长方形表示1米，用小数来表示，现在是多少米？

生：1.0米。

出示图2。

师：现在涂色部分表示多少米？

生：0.2米。

上述教学环节借助长方形，使学生清楚地感受到“把一个图形平均分成10份，这样的几份都可以用小数来表示”，丰富了教學素材，且富有逻辑性和数学味，为学生认识小数的意义打下扎实的基础。

三、借助抽象，深度理解小数的本质

抽象是舍弃个别的、非本质的属性，提取出事物中共同的、本质的属性的过程，是形成概念的有效手段。教师可以采用对比、夸张和抽象的方式来突出事物的本质属性，实现学生深刻理解数学概念的目的。

依次出示图3的三个图形。

师：学到这里，你觉得上述圆中的每份是否都可以用一个小数来表示？上述长方形中的1份或几份是不是也能用一个小数来表示？上述线段中的每个点都可以用一个小数来表示吗？

学生判断。

师：上述图形有什么相同的地方？什么样的分数可以用小数来表示？

生：上述图形都平均分成了10份，十分之几可以用小数来表示。

概括的过程是学生加深认识的过程，也是他们自主建构知识的过程。要让学生清晰、牢固地建构自己的知识体系，教师需要适时使用抽象和概括的教学手段，使学生准确把握数学概念。有了初步的感悟，再加上清晰的表达，学生对问题或概念的认识就全面、深刻了。上述图形已经脱离了具体的数量意义，有助于学生发现它们的共同特点是“都平均分成了10份”，有助于学生认识到“十分之几可以用小数来表示”。如此教学，不仅使学生深刻理解了小数的意义，还使他们积累了丰富的图形表象，建构了小数的数学模型。

总之，数形结合不仅是一种教学手段，也是一种数学思想。教师进行概念教学时可以采用数形结合的教学方式，丰富课堂的教学形式和手段，巧妙地将抽象的数学概念与图形结合起来展开教学，帮助学生感悟知识、理解概念。采用数形结合的教学方式，能让学生深刻地把握数学概念的内涵和本质，有效地建构数学知识。<＼＼Ysc02＼d＼邱＼江苏教育＼小学版＼2017＼01＼KT1.TIF>