横摇和纵摇非线性耦合下船舶运动的全局动力学

周 莎， 张 伟， 于天俊， 杨晓东

(1. 北京工业大学 机械工程与应用电子技术学院，北京 100124； 2. 机械结构非线性振动与强度北京市重点实验室，北京 100124)

横摇和纵摇非线性耦合下船舶运动的全局动力学

周 莎1，2， 张 伟1,2， 于天俊1,2， 杨晓东1,2

(1. 北京工业大学 机械工程与应用电子技术学院，北京 100124； 2. 机械结构非线性振动与强度北京市重点实验室，北京 100124)

针对横摇和纵摇非线性耦合下船舶的混沌运动，首次应用能量相位法研究了船舶动力系统在1∶2内共振，第2阶主共振情形下系统的全局分叉及多脉冲混沌动力学行为，揭示了船舶运动存在模态作用、能量转移和多脉冲混沌运动的机理，并给出了船舶系统发生多脉冲混沌运动的参数区间。数值模拟验证了横摇和纵摇非线性耦合下船舶运动系统存在多脉冲混沌运动。

船舶动力学；非线性耦合；能量相位法；多脉冲混沌运动

纵浪尤其是迎浪航行是船舶最为常见的航行状态，若按传统的线性理论，由于没有受到横向干扰力，船舶横摇运动幅值应该近似为零。但许多航海记录及模型试验都发现了船舶在纵浪中也会产生横摇运动。FROUDE[1]首次在船模实验中发现纵浪中的船模纵摇运动与横摇运动相互耦合。PAULLING等[2]将纵摇视为谐和运动，并忽略阻尼的影响，得到了参数激励的Mathieu方程。NAYFEH等[3]，研究了规则纵浪中，考虑阻尼因素的横摇及纵摇耦合动力学方程，利用多尺度方法研究发现，当船舶纵摇频率接近横摇频率两倍且波浪频率接近纵摇频率时，存在纵摇运动“饱和”及能量向横摇运动渗透的现象。YANG等[4]针对轴向运动梁的纵向与横向耦合非线性动力学的研究也发现此类现象。

除前述的船舶非线性动力学系统稳态运动下不同模态间通过内共振发生能量相互传递外，船舶横摇及纵摇运动相互耦合下会发生复杂的混沌运动，此前的学者主要针对横摇运动的非线性动力学模型，利用微分动力系统理论、分叉及混沌理论来研究横摇运动，取得了很大进展[5-6]，但考虑横摇及纵摇非线性耦合下开展相应高维系统混沌的解析预测尚未见报道。

能量相位法[7-10]是研究高维非线性系统全局分叉和多脉冲混沌运动的一种全局摄动方法。能量相位法以相位准则和能量准则为前提，解析的预测工程实际问题中混沌振动出现的条件。

本文首次将能量相位法应用于横摇和纵摇非线性耦合下船舶动力学模型，研究了该动力学系统在1∶2内共振，第2阶模态主共振的情形下系统的全局分叉和多脉冲混沌动力学行为，揭示了船舶运动存在模态作用、能量转移、多脉冲跳跃和多脉冲混沌运动的机理，并给出了船舶动力学系统发生多脉冲混沌运动的参数区间。

1 标准方程

NAYFEH等[11]给出了船体在频率为Ω的规则波浪下绕纵轴的横摇u1和绕横轴的纵摇u2的动力学方程为

(1)

式中:Fi(i=1,2)为激励幅值;τi(i=1,2)为相位。

考虑式(2)共振关系

ω2=2ω1+εσ1,Ω=ω2+ε2σ2

(2)

和尺度变换

μ1→εμ1,μ2→εμ2,F1→εF1,F2→εF2,0<ε≪1

应用多尺度方法和正则变换可将式(1)转化为扰动哈密顿方程的标准方程

(3a)

(3b)

(3c)

(3d)

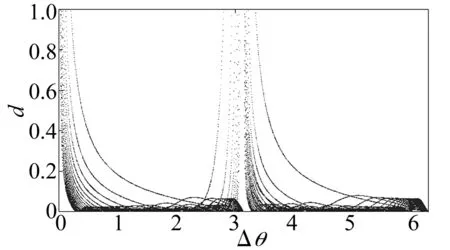
式中:α=1/2Ω;f=F2/8Ω，哈密顿函数及耗散项为

(4a)

(4b)

gp=-2μ1p，gq=0

(4c)

gI=-2μ2I+(μ2-μ1)p，gθ=0

(4d)

2 能量相位法

2.1 未扰系统动力学

首先研究未扰动系统，即当ε=0时系统的动力学行为。

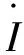
对于(p,q)平面，参数σ1决定着平衡点的个数。

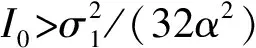
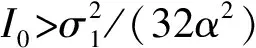
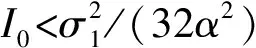
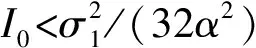
其中,

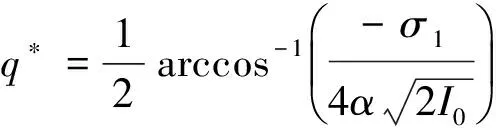
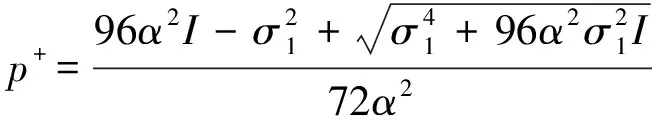
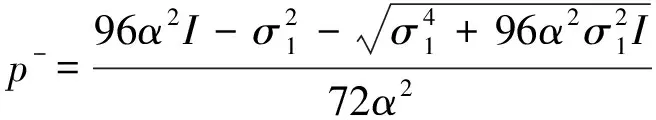
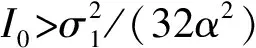
图1 未扰动系统相图Fig.1 The phase portrait of unperturbed system

未受扰动系统相轨线

q(t)=

(5)

(6)

θ(t)=θ0-2q

(7)

此时，未扰动系统存在二维法向双曲不变流形

M01=

(8a)

和

M02=

(8b)

限制在不变流形M0上的动力学方程为

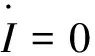
(9a)

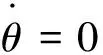
(9b)

则不变流形上的点均为不动点，且连接任意两不动点的异宿轨道的相位差，即相位漂移角为

Δθ=θ(+∞)-θ(-∞)=

(10)

2.2 扰动系统动力学

根据法向双曲不变流形在小扰动下不变流形的保持性，对于充分小的ε>0，法向双曲不变流形扰动为

(11a)

和

(11b)

限制在不变流形Mε上的动力学方程为

(12)

式(12)存在不动点

(13)

该不动点的特征方程为

故当μ2>0且σ2≠0时，不动点pε是稳定的焦点。因此流形Mε上的轨线趋于点pε。

下面验证同宿于流形Mε的N-脉冲同宿轨的存在性。能量差分函数为

(14)

能量差分函数存在横截零点，即式(14)满足

ΔNH(I,θ)=0,DθΔNH(I,θ)≠0

(15)

式(3)存在同宿于流形Mε的N-脉冲同宿轨。

接下来，验证船舶动力学系统存在着以不动点pε为起跳点，且降落点在不动点pε的吸引域内的ilnikov同宿轨的存在性。

为确定从不动点pε起跳的ilnikov同宿轨，需要找到参数向量λ=(σ1,d,ξ)，使得参数向量λ满足

ΔNH(Iε(λ),θε(λ),λ)=0

(16a)

D(I,θ)ΔNH(Iε(λ),θε(λ),λ)≠(0,0)

(16b)

即

d2(sin2(NΔθ)-N2sin2(Δθ))+ξ2(cos(NΔθ)-1)2-

2dξ(cos(NΔθ)-1)sin(NΔθ)=0

(17a)

(17b)

式中:d=μ2/f;ξ=σ2/f。

(a) ξ=0.1

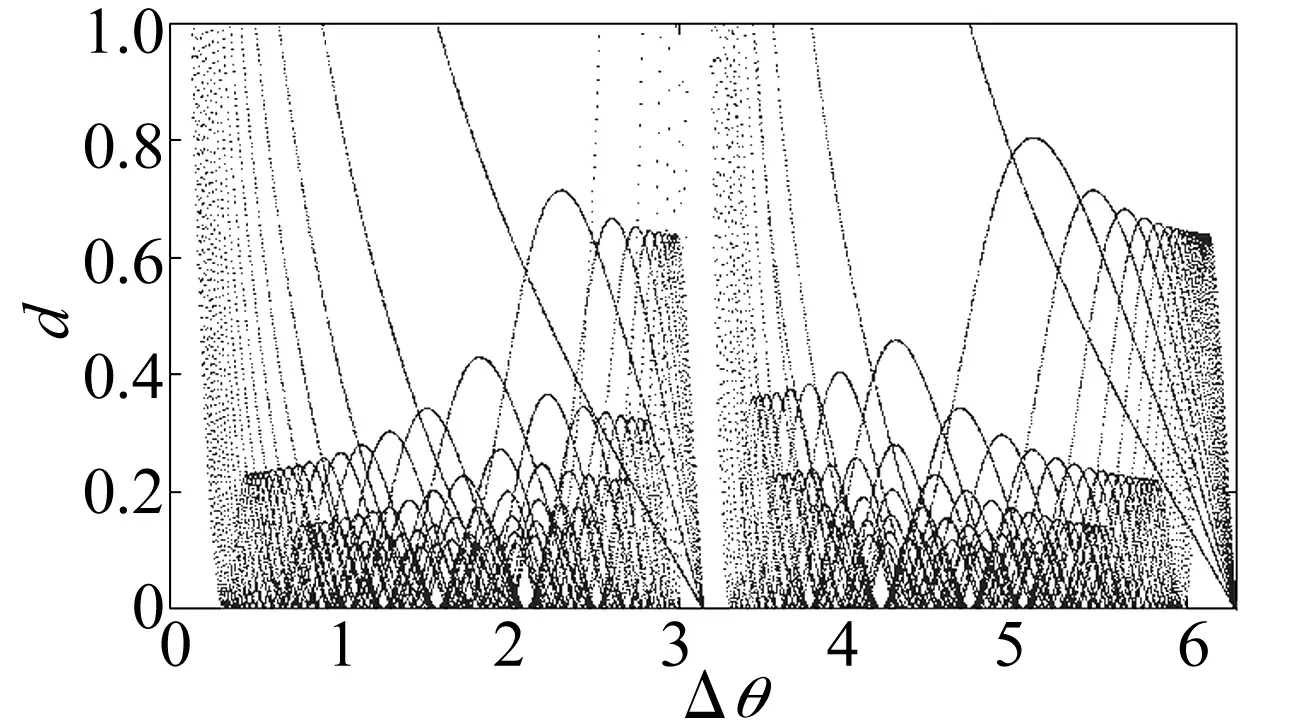
(b) ξ=1图2 多脉冲混沌运动的参数区间Fig.2 Parameter region of the multi-pulse chaotic motion

3 数值模拟

利用四阶Runge-Kutta数值积分方法对式(4)进行数值模拟，验证横摇和纵摇非线性耦合下船舶动力系统存在多脉冲混沌运动，以及模态之间的相互作用和能量传递。

选取参数ω1=0.25，σ1=1，σ2=0.3，F2=1,εμ2=εμ1=0.002,图3(a)为(p,q)平面的相流，图3(b)为庞加莱映射，图3(c)为(p,I,θ)空间的相流。图3表明扰动系统存在异宿轨破裂，稳定流形及不稳定流形横截相交导致的多脉冲混沌运动。图4为横摇和纵摇两模态的位移响应随时间的变化情形，明显地，船舶横摇和纵摇两模态之间存在相互作用及能量传递。

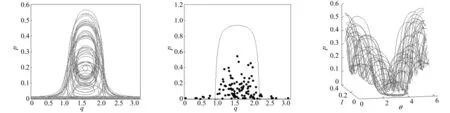
(a) (p,q)平面扰动系统相流 (b) 庞加莱映射 (c) (p,I,θ)空间扰动系统相流图3 动力系统数值模拟Fig.3 Numerical simulations of dynamical system

图4 横摇和纵摇模态响应Fig.4 Response of pitch and roll modes

4 结 论

针对横摇和纵摇非线性耦合下船舶的混沌运动，首次应用能量相位法研究了船舶动力系统在1∶2内共振，第2阶主共振情形下系统的全局分叉及多脉冲混沌动力学行为。

首先，应用多尺度方法和正则变换将非线性耦合的船舶运动方程转化为扰动哈密顿方程的标准形式。其次，应用能量相位法研究船舶的多脉冲混沌运动,发现系统在未受扰动情形下存在双曲鞍点和连接鞍点的异宿轨，在小扰动的情形下异宿轨发生破裂；能量差分函数横截零点的存在确保异宿轨破裂后其稳定流形和不稳定流形横截相交，且存在着同宿于慢流形的多脉冲同宿轨；进一步验证船舶动力系统存在ilnikov同宿轨，这意味着该系统存在Smale马蹄意义下的混沌运动，并给出多脉冲混沌运动发生的参数条件。数值模拟验证了理论分析。本文的研究揭示了船舶运动存在模态相互作用、能量转移和多脉冲混沌运动的机理。

[ 1 ] FROUDE W. Remarks on Mr. Scott Russell’s rolling[J]. Transactions of the Institute of Naval Research, 1863, 4: 232-275.

[ 2 ] PAULLING J R, ROSENBERG R M. On unstable ship motions resulting from nonlinear coupling[J]. Journal of Ship Research,1959, 3(1): 36-46.

[ 3 ] NAYFEH A H, MOOK D T, MARSHALL L R. Nonlinear coupling of pitch and roll modes in ship motions[J]. Journal of Hydronautics, 1973, 7(4): 145-152.

[ 4 ] YANG X D, ZHANG W. Nonlinear dynamics of axially moving beam with coupled longitudinal-transversal vibrations[J]. Nonlinear Dynamics, 2014, 78: 2547-2556.

[ 5 ] NAYFEH A H, SANCHEZ N E. Stability and complicated rolling resonses of ship in regular beam seas[J]. International Shipbuilding Progress, 1900, 37: 331-352.

[ 6 ] FALZARANO M, SHAW S W, TROESH A W. Application of global methods for analyzing dynamic systems to ships rolling motion and Capsizing[J]. International Journal of Bifurcation and Chaos, 1992, 2: 101-115.

[ 7 ] HALLER G, WIGGINS S. Orbits homoclinic to resonances: the Hamiltonian case[J]. Physic D Nonlinear Phenomena,1993, 66(3/4): 298-346.

[ 8 ] HALLER G, WIGGINS S. N-pulse homoclinic orbits in perturbations of resonant Hamiltonian systems[J]. Archive for Rational Mechanics and Analysis, 1995, 130(1): 25-101.

[ 9 ] HALLER G, WIGGINS S. Multi-pulse jumping orbits and homoclinic trees in a modal truncation of the damped-forced nonlinear Schrödinger equation[J]. Physic D Nonlinear Phenomena, 1995, 85(3): 311-347.

[10] HALLER G. Chaos near resonances[M]. New York: Springer-Verlag, 1999.

[11] NAYFEH A H, MOOK D T. Nonlinear oscillations[M]. Germany: Wiley-VCH, 1995.

Global dynamics of ship motions considering the nonlinear coupling between pitch and roll modes

ZHOUSha1,2,ZHANGWei1,2,YUTianjun1,2，YANGXiaodong1,2

(1. College of Mechanical Engineering, Beijing University of Technology, Beijing 100124, China; 2. Beijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures, Beijing 100124, China)

The global dynamics of ship motions considering the nonlinear coupling between pitch and roll modes in the presence of one to two internal resonance and principal resonance of the second mode were investigated using the energy-phase method. A major goal of the paper was to reveal the mechanism about modes interaction, energy transfer and multi-pulse chaotic motions of the ship. The certain parameter regions in which multi-pulse chaotic motions that might occur were given. Numerical simulations were performed to confirm the theoretical predictions.

ship dynamics; nonlinear coupling; energy-phase method; multi-pulse chaotic motion

国家自然科学基金资助项目(11290152;11322214);北京市高等学校人才强教计划资助项目(11072008)

2015-11-09 修改稿收到日期：2016-01-27

周莎 女，博士，1986年7月生

张伟 男，博士，教授，1960年7月生

O322； O415.5

A

10.13465/j.cnki.jvs.2017.04.034