数值计算结合试验测定模态阻尼法

唐宇航， 陈志坚， 梅志远， 孙建连

(1.海军工程大学 舰船工程系，武汉 430033; 2.国网蚌埠供电公司，安徽 蚌埠 233000)

数值计算结合试验测定模态阻尼法

唐宇航1， 陈志坚1， 梅志远1， 孙建连2

(1.海军工程大学 舰船工程系，武汉 430033; 2.国网蚌埠供电公司，安徽 蚌埠 233000)

任一种分布的激励必将引起多个模态的响应，试验中要激出单一模态振动是很难的，传统阻尼比估算方法所采用的信号处理手段不能有效分离叠加模态，以致测试阻尼比往往误差较大。从多自由度叠加法动响应分析入手，指出模态混叠现象是制约精确阻尼比测试的重要因素，在阻尼较大、刚度较低时模态更密集、叠加效应更显著，提出通过数值计算进行模态截断以实现“纯模态”提取的方案，推导了共振激励下试验与数值仿真结果中频响峰值谱线表达式，找出二者间的关系，用纯模态计算结果修正测试阻尼比。通过对4块不同板单元进行前8阶试验模态分析与数值计算参数修正，结合频响函数验证了修正阻尼比的数据可靠性，得出了不同结构、材料间阻尼比差异的部分规律。结果表明,模型试验对复合材料板的阻尼比识别准确性要低于钢板，其阻尼性能往往被低估且修正幅度较大，该方法为模态参数识别的进一步研究提供了思路。

数值计算；模态阻尼比识别；频响曲线；模态截断；模态叠加

阻尼参数作为一项重要的动力性能指标，对结构在共振区的响应影响十分显著，目前其取值常依靠经验，具有一定的局限性，对特殊结构的振动响应预报缺乏借鉴意义[1]。因此，阻尼参数的取值亦常需要通过试验来测定，然而试验条件的微小差异均可能会造成测量结果的巨大偏差。虽然国内外也制定了相关行业标准，但事实上并没有成为科研和生产上严格执行的规范[2-3]。实际工程结构阻尼成分复杂，一般是由内部阻尼(材料)、结构阻尼以及流体阻尼综合决定[4]，然而现有阻尼测试标准(如GB/T 18258—2000、GB/T 16406—1996、GB/T 13665—2007、GB/T 17809—1999)多是针对试件的材料阻尼测量，有扭摆法、弯曲振动法、悬臂梁共振法、复模量图示法和相位法[5]等，按照已有标准得到的阻尼参数在工程中往往难以直接运用，因此在寻找优良的阻尼材料以实现减振降噪等效果的同时，探究可靠实用的阻尼测试方法也十分紧迫。

模态阻尼比是多自由度系统动力分析中模态叠加法求解响应问题的重要参数，现有的设备和不同的测试方法在识别该参数时存在不稳定的现象，时常得到差异巨大的模态阻尼比结果，其信号处理手段可依频域和时域两大类划分[6]。

频域下常通过对一组激振和拾振点间的频响函数进行信号处理计算出各模态参数，方法主要包括峰值拾取法、导纳圆法、整体多项式拟和法或复指数拟和法等。其中，前两者为单自由度图解法，适用于模态不密集、小阻尼结构；后两者为多自由度解析法，适用于模态密集、大阻尼结构。峰值拾取法依赖于半功率法阻尼估算理论，陈奎孚等[7-9]对该理论精度和误差进行了分析，认为离散谱线难以获得精确的半功率点、窗阻尼影响以及数字信号处理手段上的差异等，均会导致阻尼估算的偏差达到几倍甚至几十倍，得到错误结论。导纳圆法计算精度受图解精度的限制，且无法避免因邻近模态叠加所产生的误差[10]。拟合解析法常用于处理多自由度系统，然而一般为得到密集模态的信息会增加测点数目，这一举措在增大了计算量的同时，也易产生病态的转换矩阵从而影响参数识别精度[11]。

时域下的参数识别主要有对数衰减法、自由衰减法、随机减量法等，在进行多自由度模态分析时需使用窗函数对时域信号进行滤波处理，经典窗可以辨识一般结构的模态参数，但在分离低频密集模态、叠加模态时精度较差，特别是位于频响函数的两端且很接近的模态[12-13]，文献[14]基于WT(Wavelet Transformation)理论讨论了时频分辨率及端点效应问题，应用AWT(Analytic Wavelet Transformation)准确识别阻尼参数的前提是具备高精度的随机减量信号。WANG等[15]研究了一种仅运用结构自由振动信息识别多阶模态参数的方法，利用离散的时序信号将广义特征值问题转为一般特征值问题。陈茉莉等[16]从时域理论入手，对压气机叶片的自由振动高频模态成分进行分析，在忽略部分振型分量后逐步从原始数据中“剔除”已识别模态成分，再利用时域衰减法依次计算出前8阶模态阻尼比。黄方林等提出一种仅测量输出点的时域响应信号，计算其与时间轴所围面积关系确定阻尼比的方法，抗干扰能力强、精度高、结果稳定。

在试验中激起多自由度系统的“纯模态”几乎是不可能的，任一激励下的响应必将是多个模态响应的叠加，已有研究多是运用信号处理的方法试图将叠加模态分离出来，难以避免理论上的缺陷或繁琐的运算。本文提出了一种数值计算结合试验测定模态阻尼比的方法，利用程序中关于模态截断的PCL(Patran Command Language)语言进行指定阶次响应分析，以分离叠加模态得到“纯模态响应”，推导出试验数据的频响峰值与数值分离所得“纯模态”频响峰值谱线间的关系，对模态阻尼比进行识别和修正。在此基础上结合潜艇外壳辐射噪声的实际计算需求，完成了4块不同厚度、材质的船体典型局部板单元前8阶模态阻尼比计算。

1 试验设计

1.1 试验背景

潜艇在水下航行时，外壳振动所辐射出的噪声是设计师们关注的重点，其振声性能直接关系到潜艇航行的安全性和隐身性。由于板壳材质、厚度等在全船范围内分布复杂，直接用经验取值描述总体阻尼偏离实际且误差较大，淡丹辉等[17]提出单元化的阻尼比法则在控制结构总体模态阻尼比方面更具优势，可在对多阶模态阻尼比精确控制的同时又能解决分布式阻尼的建模问题。因此为对潜艇辐射噪声进行更加可靠的预报，在计算壳体表面振动响应前应了解其实际阻尼分布情况，有必要对船体典型板单元结构进行阻尼比测试。按照相关规范，在进行整船有限元建模时板壳网格尺寸常按一个纵骨或一个肋位间距(500 mm左右)小者划分，且尽量接近正方形。本试验以此为依据构造典型板单元阻尼比测试模型，如图1所示。

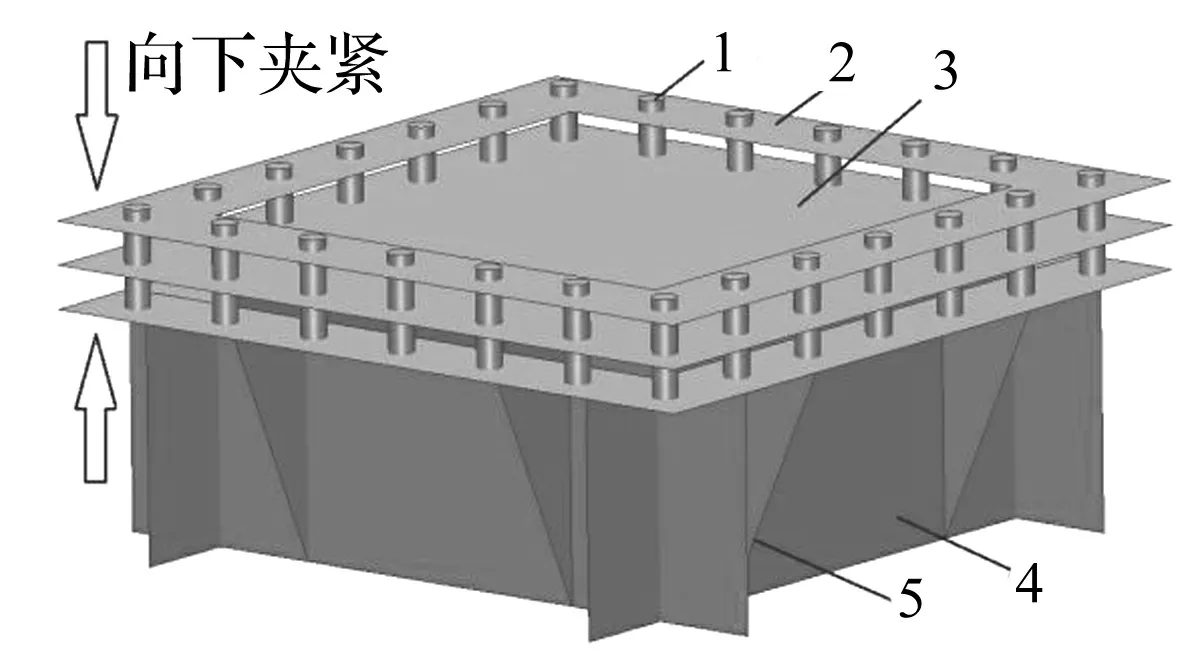
1-螺栓;2-压条;3-板单元试件;4-基座;5-支撑加强结构图1 试验模型空间示意图(测试内区域500 mm×500 mm)Fig.1 Experimental model spatial schematic diagram (test area 500 mm×500 mm)

1.2 试验环境

试验分别对500 mm×500 mm×3 mm规格Q235钢板及与其等厚度、等刚度、等质量的3块E800/350环氧树脂材质的玻璃钢板进行多阶模态阻尼比识别。板单元模型尺度参数见表1。构造固定的边界条件以模拟板在实船中与周围肋骨等骨架的连接状况，使用24根螺栓将板紧固在基座与压条之间，注入玻璃胶填充缝隙以防止频段内漏声造成的误差。为避免试验激励时板带动基座产生耦合共振现象，基座使用15 mm厚度钢块焊制并在四周设置了支撑结构以增加其质量和刚度，控制其首阶自振频率在1 kHz以上，保证与各板单元前8阶自振频率有足够的错开率，试验模型如图1所示。

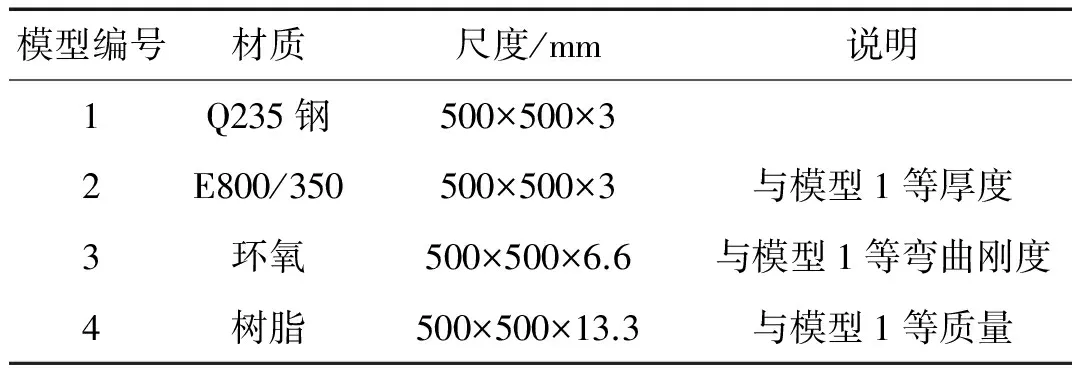
表1 板单元试验模型尺度参数

试验测试系统的构成如图2所示。第1步采用多点激励多点拾振的方法(以辨别对称结构模态重根)进行模态测量，得到各阶共振频率和振型，力锤的脉冲激励可以触发结构宽频带自由振动，响应信号区分度高、识别清晰，板背面布置3个拾振点，正面依次敲击81个激振点(见图3)。第2步采用共振驻留法进行各阶共振激励，传感器的布置根据事先进行的数值计算确定，既位于邻近模态的“节点”、“节线”处，亦为各阶振型下具有明显响应的位置，在板背面布置9个测点(见图4)。所有测点信号均用加速度传感器采集。

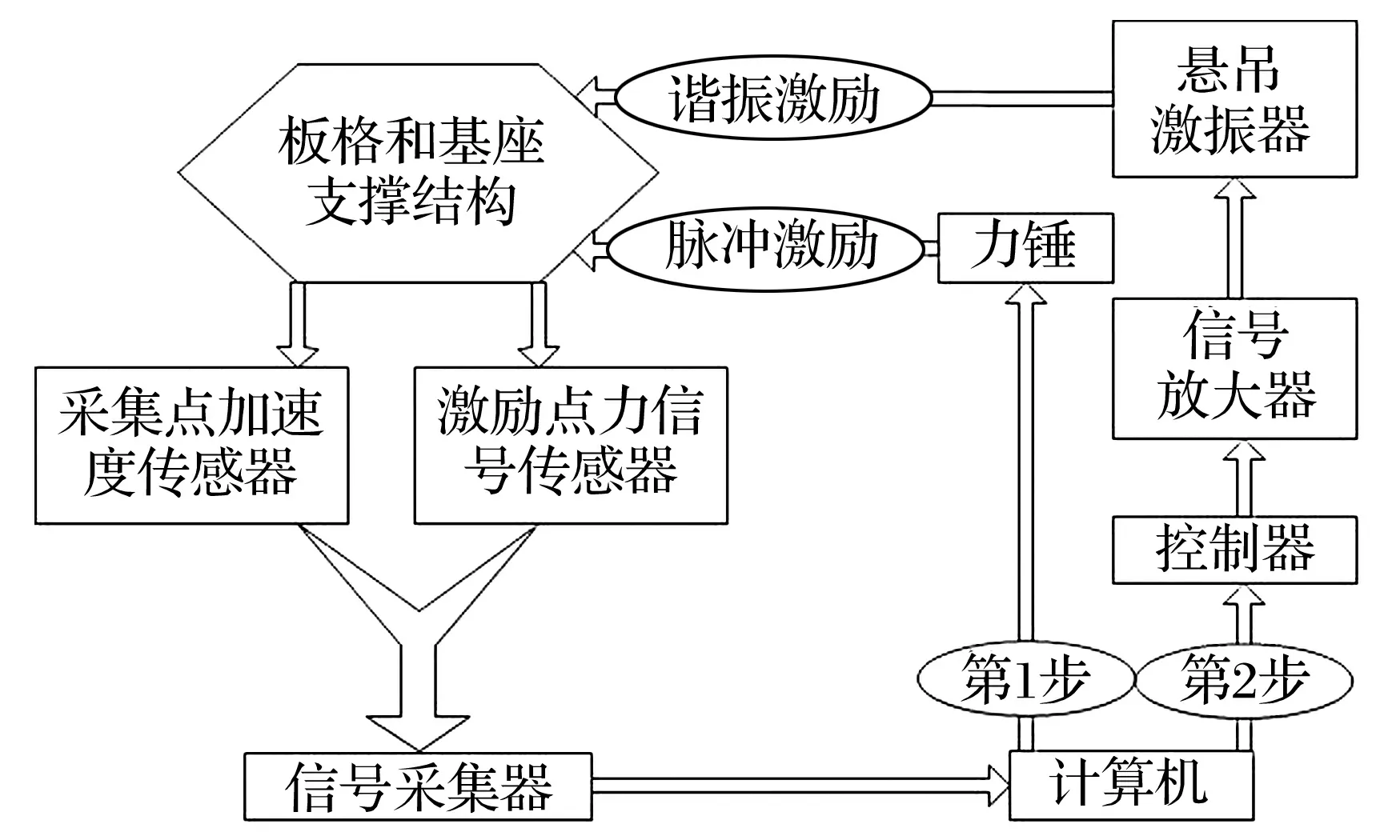
图2 板单元模型测试系统的构成Fig.2 Experimental system constitution of plate element model

图3 脉冲激励试验(模型1)Fig.3 Pulse excitation experiment (model 1)

图4 共振激励试验(模型2)Fig.4 Resonance excitation experiment (model 2)

2 数值分析

2.1 有限元模型建立及模态分析

钢材板与复合材料板的材料性能差异较大，试验使用正交各向异性复合材料，计算时考虑纤维铺层方向、角度和厚度等，其与钢板相关参数在表2中给出。数值计算时对试验模型进行整体有限元建模，模拟空气中的振动情况，试件采用板单元、传感器等集中质量用0Dmass单元进行模拟。谐振激励试验按各阶振动响应明显位置进行激励和采集，数值仿真时按照与试验模型上相对应的位置计算，并建立有限元模型。

数值计算时先对4块板进行模态分析，得到前8阶振型和固有频率，各板振型相似，表3给出了各板单元试验和仿真计算固有频率对比以及模型2振型图对比结果。由表3可见，试验与数值计算的各对应阶次振型基本一致；固有频率结果存在小范围相对偏差(<5%)，认为试验模型与仿真模型匹配度高，频率的相对误差主要源于试验中固定边界不理想、人工网格划分有误差和集中质量分布不对称等因素。对比钢板与复合材料板可见，后者的部分阶次计算相对误差更大些，这是由于板材质的各向异性、生产工艺上偏差等因素对试验结果产生了影响。

表2 玻璃钢板与普通钢板材料性能参数

Tab.2 Material performance parameters of glass fiber plate and common steel plate

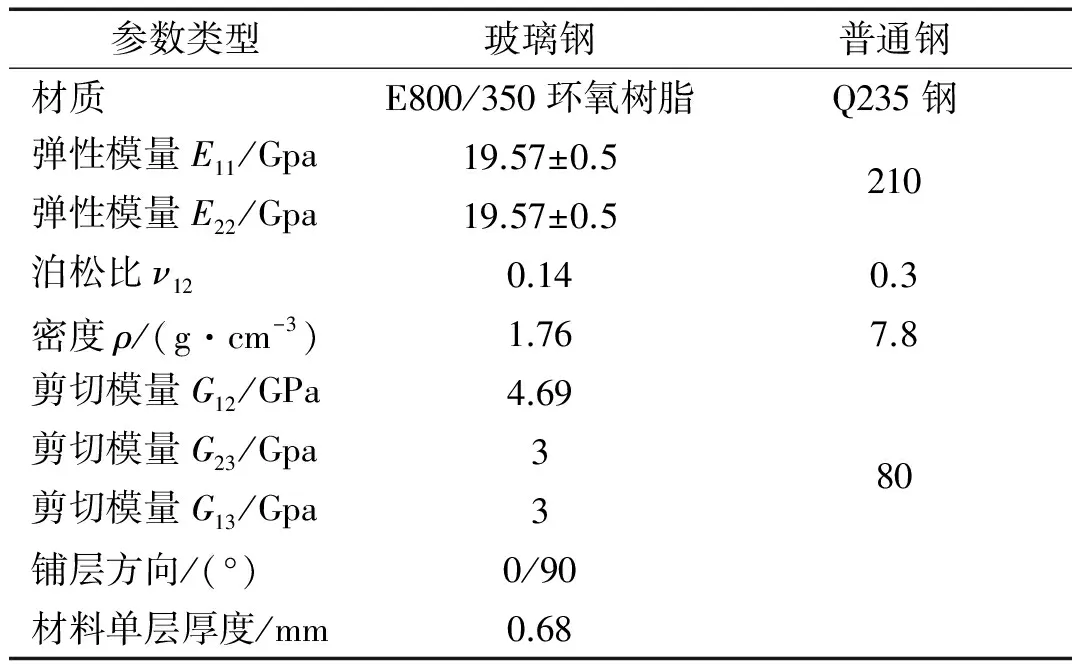
参数类型玻璃钢普通钢材质E800/350环氧树脂Q235钢弹性模量E11/Gpa19．57±0．5210弹性模量E22/Gpa19．57±0．5泊松比ν120．140．3密度ρ/(g·cm-3)1．767．8剪切模量G12/GPa4．69剪切模量G23/Gpa380剪切模量G13/Gpa3铺层方向/(°)0/90材料单层厚度/mm0．68

2.2 共振激励计算单一模态响应

对比各板单元试验与数值计算的振型和固有频率结果对应一致后，进行共振激励计算。针对各阶振型特点，按照与试验中相对应的位置进行瞬态分析，及响应的频域转换。试验中采集激振-拾振点时域信号后按力幅归一化进行频域转化得到频响函数，数值计算时施加单位共振激振力，激振、拾振点见表3。运用模态叠加法进行总响应分析前，采用Msc.Nastran中PCL语言的mode select语句对计算文件进行模态截断，选择关心的某阶(或某几阶)模态进行响应计算。求解模态阻尼比时，精度较高的方法往往受单自由度理论的限制，这种模态选择的方法可以在计算总响应前完成各模态分量的分离，精确地得到各阶“纯模态”下的结构响应，方便定向地研究指定阶次的模态参数问题。

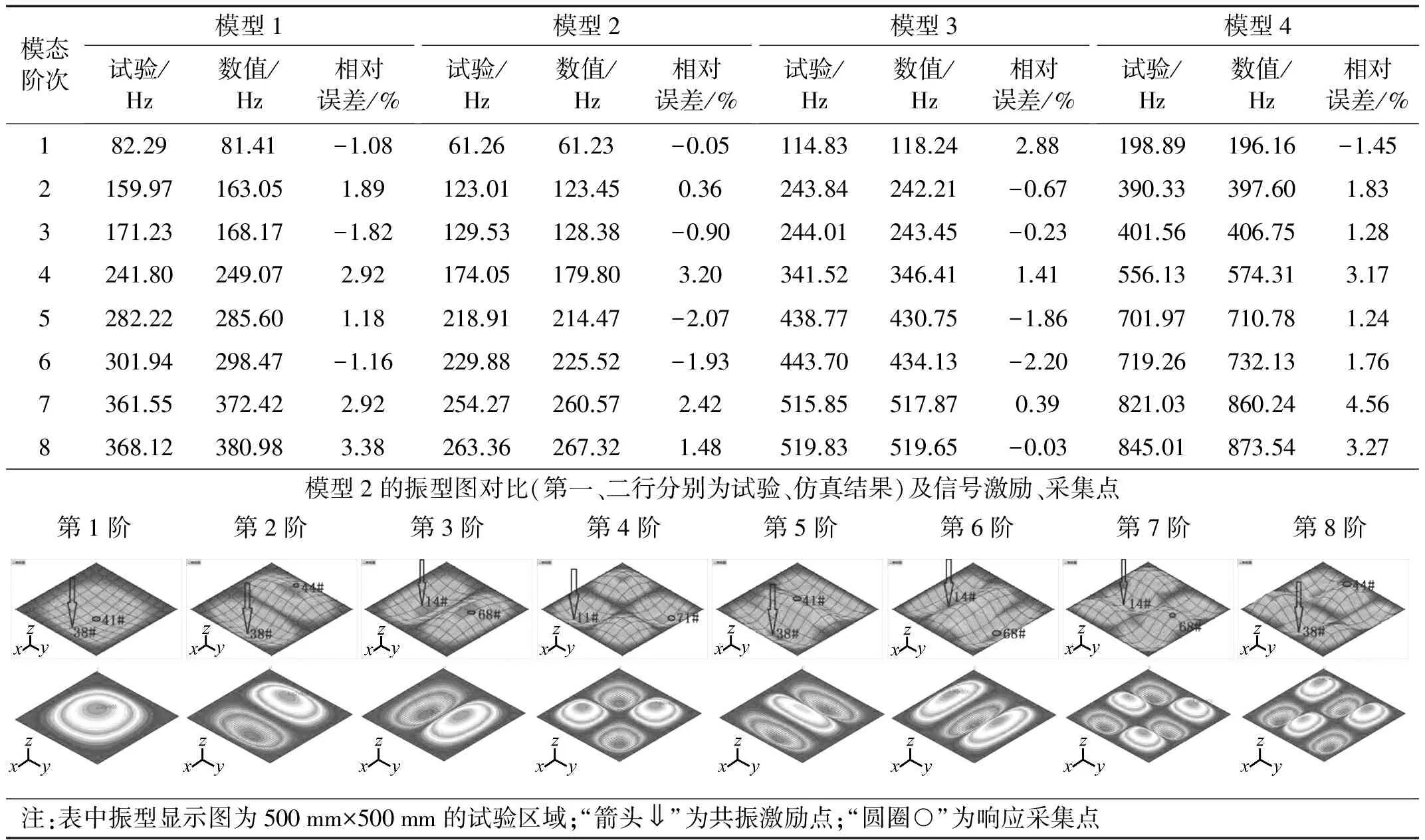
表3 4块板单元模型前8阶固有频率的试验与仿真对比结果

3 数据处理方法

3.1 模态混叠下阻尼比误差分析

密集模态混叠原因有两个:①各阶模态的固有频率靠的太近;②各阶模态的阻尼比较大[18]。当出现以上情况时，则会在频域上出现多个峰的相互叠加(见图5)，直接运用传统的阻尼估算方法就会带来较大的误差。文献[19]在兼顾了频率及阻尼比对模态混叠程度的影响下，按图5对模态密集度进行了定义

(1)

将λ>1的模态视为密集模态，分析此时无法使用带通滤波的时域法进行阻尼比计算。

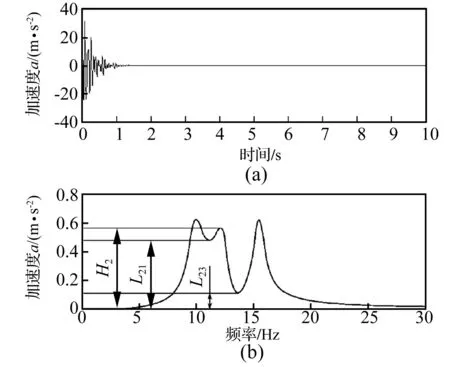
图5 模态密集度的定义Fig.5 The definition of modesclosely degree

为明确模态混叠对传统阻尼识别方法所产生的偏差影响，验证“纯模态”响应提取结果的可靠性。以模型4为例，设定其第4～8阶模态阻尼比为0.007，并对该频段进行数值仿真频响分析，考察某一“激振-拾振”点间的频响特性，用半功率法对该频响反推模态阻尼比，同时将各阶“纯模态”频响与总频响进行对比，如图6所示，计算结果见表4。从表4可见，第4阶模态与其余阶次混叠程度较轻(λ较小)，使用半功率法识别准确，对模态混叠严重的第7～8阶模态，难以获取正确的半功率点，误差很大；从频响曲线上看，总频响中第4阶附近曲线与该阶“纯模态”频响高度一致，验证了纯模态计算准确可靠，受叠加影响，较高几阶频响与纯模态频响差异较大。此外，由于各阶振型间存在相位差，总频响并不是各纯模态频响的直接叠加，对半功率带宽的影响也存在差异，总之模态密集度越高(λ越大)，半功率法识别精度越差。

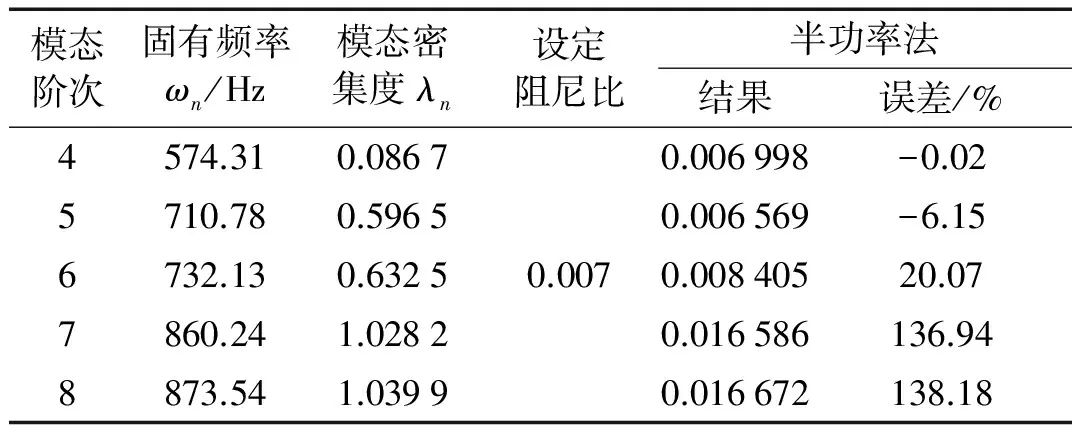
表4 半功率法估算密集模态阻尼比误差分析

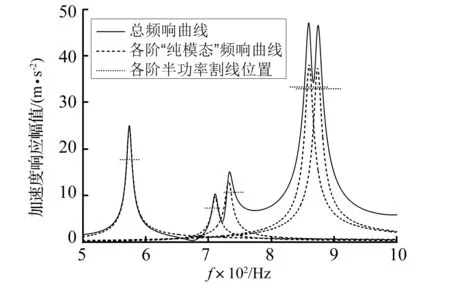
图6 模型4第5～8阶总频响与纯模态频响对比(11#-71#)Fig.6 Comparison of total and pure mode frequency response during 5th to 8th frequency spectrum of model 4(11#-71#)

3.2 傅里叶变换下的传递函数

结构的动态特性可由N阶矩阵微分方程描述

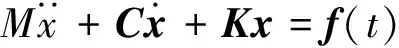
(2)

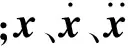
设系统的初始状态为零，对式(2)两边进行拉普拉斯变换，可以得到以复数s为变量的方程

Z(s)X(s)=H(s)-1X(s)=F(s)

(3)

其中,

Z(s)=H(s)-1=[Ms2+Cs+K]

(4)

式中:Z(s)为广义阻抗矩阵;H(s)为广义导纳矩阵，也就是传递函数矩阵。令s=jω，由式(3)得到频域中输出和输入的关系

X(ω)=H(ω)F(ω)

(5)

式中,H(ω)为频率响应函数矩阵，第i行第j列的元素(指仅在j坐标单位激励下，i坐标频响曲线)为

Hij(ω)=Xi(ω)/Fj(ω)

(6)

由式(4)得阻抗矩阵

Z(ω)=(K-ω2M)+jωC

(7)

令振型矩阵Φ=[φ1,φ2,…,φN]，则

(8)

因此，

(9)

式中:rHij(ω)为r阶模态对Hij(ω)的贡献;Yr为r阶模态导纳;mr、kr、cr和φr分别为第r阶模态的质量、刚度、阻尼和振型;γr为激励频率与固有频率之比;ζr为模态阻尼比。N自由度系统的频率响应，等于N个单自由度系统频率响应的线性叠加。

以上给出了任意频响函数的叠加公式，可见任一点的频响函数中均含有所有阶次的模态响应成分，因此对于多自由度系统，想要激起单一模态响应是不实际的。测试系统频响函数的获取是基于能量的角度对线性系统的输入与输出进行频域描述，即

Hxy(ω)=Gxy(ω)/Gxx(ω)

(10)

式中:Gxy(ω)为互谱，是对两个周期信号在频域上相关性的描述；Gxx(ω)为自谱(功率谱)，是对周期信号在频域上的分布性描述。

其中，

(11)

(12)

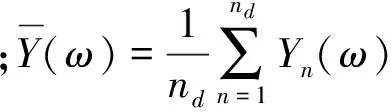
对拾振点响应进行离散傅里叶变换(Q为傅里叶变换的点数)。即

(13)

将式(11)～式(13)代入式(9)

Hxy(ω)=Hxy(kΔω)=

(14)

测试系统同时测量了激励、响应信号，按式(14)将时域信号通过傅里叶变换转化成频域上有限个点，得到各测点的频响曲线。基于试验所测信号所得的频响曲线Hxy(ω)在理论上仍依赖于式(9)中的模态叠加规律。即

(15)

3.3 阻尼比修正方法

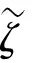
(16)

总响应为

小阻尼理论假设下，以低阶共振频率激励时，系统响应主要来源于当前阶的模态响应贡献[20]。本文试验对振型响应较显著的位置进行激励，拾振点布置在邻近模态的“节点”或“节线”处，则响应中该阶模态成分占比更高，因此式(17)可近似写为

(18)

式中:rx(t)为r阶模态的测点时历响应;rxst为静载荷p作用下测点位移。可见rx(t)时域最大值为rxst(1/2ζr)，将其代入式(13)进行频域变换，得到r阶固有频率处所对应的频率响应谱线表达式

(19)

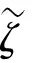
(20)

根据式(19)～式(20)化简得

(21)

试验所得阻尼比是含有模态叠加影响因素的近似值，通过使用数值计算中模态选择语句，实现仅对r阶“纯模态”进行响应计算，对比试验与仿真在频域下该阶次共振频率ωr处响应谱线峰值可完成阻尼比的修正。

4 测试数据及结果

4.1 共振驻留试验响应分析对比

按照试验顺序分步使用力锤施加脉冲激励、激振器施加谐振激励，采集指定测点的加速度时序信号。①取3次力锤敲击下激励-响应点频响曲线的平均值；②取激振器作用下形成稳态共振响应信号后一段时长(1.639 s)数据的频响曲线结果并作3次平均，其中采样频率20 kHz，分析点数32 748，频率分辨率0.61 Hz。模态初步分析时采用半功率法计算阻尼比，对该阻尼比初值利用“纯模态”理论进行数值验证，得到模型1～4各阶振型下各共振激励拾振点的加速响应，将其与试验实测数据进行对比，如表5所示。可见，两者所得共振峰值存在差异，由模态叠加导致的阻尼比估算误差往往不可忽略。

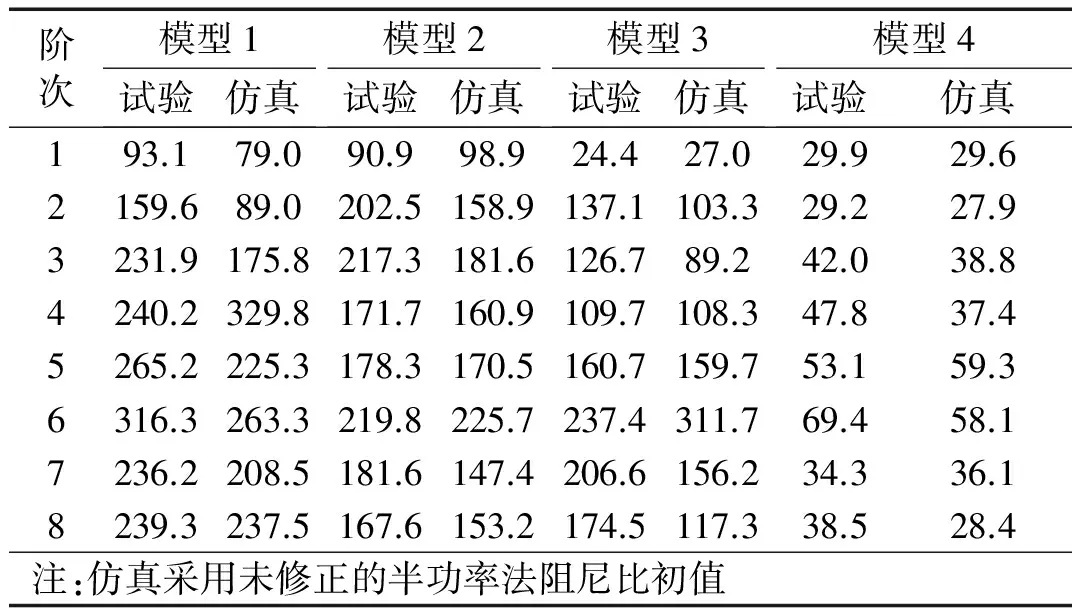
表5 模型1～4各阶实测、按阻尼比初值仿真的加速度响应

表6给出了运用半功率带宽法、带通滤波衰减法所识别的模型1～4前8阶模态阻尼比和修正后的阻尼比。可见，半功率法与衰减法识别出的阻尼比均存在一定偏差，衰减法偏差较大；由于模态混叠影响，频域下的半功率带宽较“纯模态”计算下有偏差(大多变宽)，导致部分阶次识别阻尼比偏大；从修正阻尼比来看，模型1～4，模型1(钢板)阻尼较小，受模态混叠影响较小，半功率法可以获得较为准确地结果，模型2～4(复合材料板)阻尼较大，模态混叠显著，部分阶次修正量较大。

图7给出了模型1～4修正阻尼比对比结果。可见试验中所用复合材料板的阻尼性能总体上大于钢板，其各阶模态阻尼比约为钢板的4倍左右，即模型2～4各对应阶次阻尼比相近，约为0.6%～0.9%，模型1约为0.2%～0.3%。因此在刚度满足工程需求的条件下，设计时应充分发挥复合材料优良的阻尼性能来减振降噪。实际结构振动能量耗散由内部阻尼(材料)、结构阻尼(铰链和界面处)和流体阻尼(流体-结构相互作用) 三部分阻尼机理所致。本试验中所用薄板满足二维平面假设，边界条件及四边约束下的板振型基本一致，模型1与模型2～4所表现出的阻尼比差异主要源于内部阻尼(材料内耗)；模型2～4的阻尼比差异则源于另两类阻尼耗能，瑞利阻尼模型将非线性阻尼因素考虑在内，本质上以黏性阻尼理论对结构阻尼等进行等效以解耦运动方程，按该模型得出的阻尼比与频率的关系[21]对玻璃钢板试验模型阻尼比结果进行数值拟合，如图8所示。此外，模型1～4的首阶阻尼比均大于各模型的其余阶次阻尼比，主要由于一阶振型为两个方向半波叠加，造成面内剪切变形大，且该模态为强辐射模态，对介质辐射耗能大这两方面因素所致。

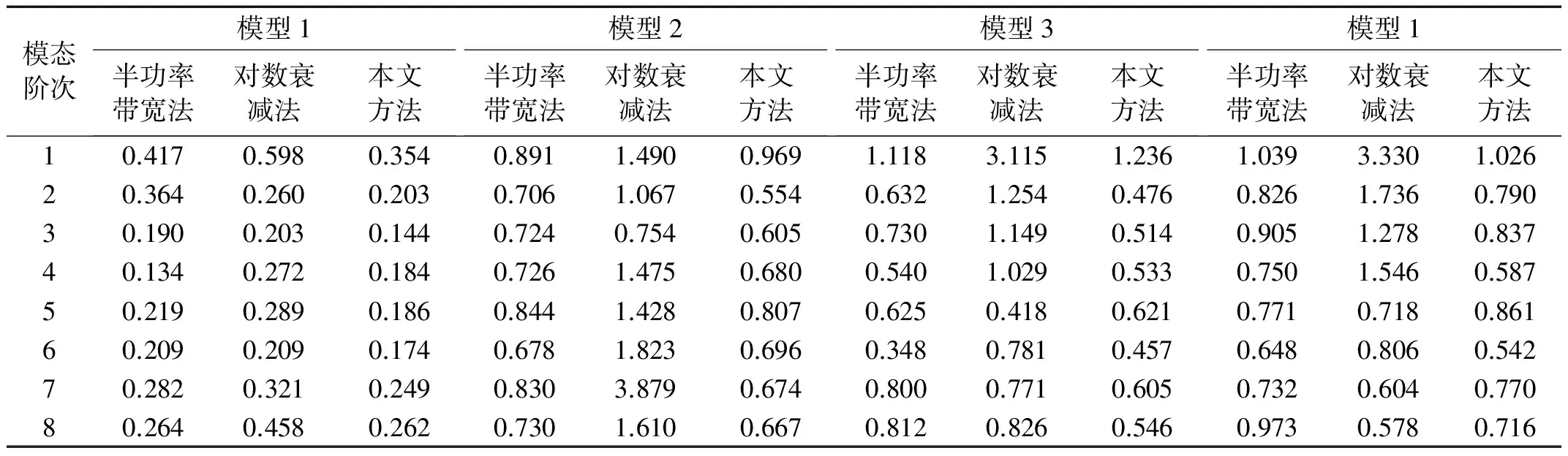
表6 4块板单元模型前8阶阻尼比修正结果与传统方法计算结果对比

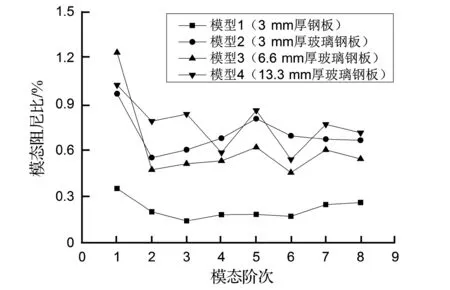
图7 3块板单元模型模态阻尼比理论修正值Fig.7 Theoretical correction values of 3 element model plates’ modal damping ratio

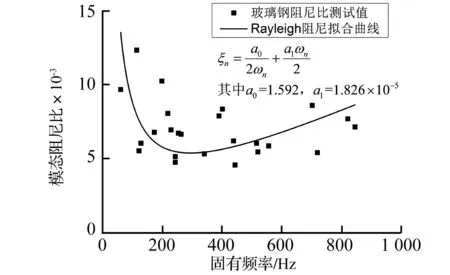
图8 阻尼比与频率的关系(Rayleigh阻尼)Fig.8 The relationship between damping ratio and frequency(Rayleigh damping)

4.2 宽频带激励下阻尼比数值验证

为验证上述阻尼修正理论的可靠性，以11#(激励)与71#(采集)测点间频响函数为例， 结合4块板脉

冲激励试验所得宽频带响应结果，与该频段内数值计算(取修正后的阻尼比)频响进行对比。4块板的频响曲线对比结果如图9所示。

图9中实线部分给出了按阻尼修正理论所得阻尼比数值计算出的频响曲线，将该曲线与试验数据对比可见，除因固有频率微小差异导致的谱线峰值小幅偏移外，曲线在峰值大小、分布形状上均与试验结果高度匹配，可认为该理论所得阻尼比较可靠。较厚的模型4板在工艺上存在轻微缺陷，个别局部振动模态对频响结果产生了一定影响，但其主振动频响同样符合规律。

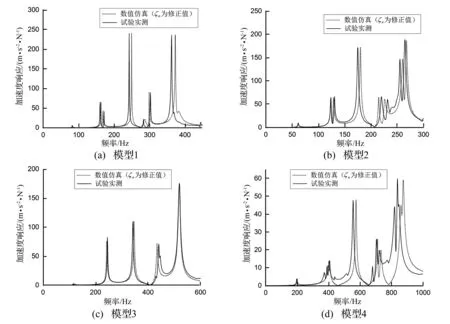
图9 模型1～4宽频带频响分析Fig.9 Broadband frequency response analysis of model No.1～4

5 结 论

目前系统模态阻尼比的获取主要依赖于试验，然而现有的测试方法、理论和软件运用于实际工程结构时具有一定的局限性，难以得到精确的阻尼比结果。本文对常用信号处理方法的缺陷进行归纳，从经典模态分析方法入手，明确了响应中“模态混叠”难以分离的现象是造成阻尼比参数识别误差的重要因素之一。另外，采用数值计算结合试验的方法，利用Msc.Nastran中模态选择语句进行模态截断，计算“纯模态响应”从而实现叠加模态的分离，按该方法结合试验对4块不同板单元前8阶模态阻尼比进行识别与修正，并通过单位脉冲下宽频带频响曲线的对比验证了修正结果的可靠性。

此外，对于这种实际船体分析时常用的典型板单元结构，其阻尼性能有如下结论：

(1)相同边界条件及结构振型下，薄板的材料是影响其模态阻尼比的主要因素，模型构件的刚度、质量分布特性对阻尼比的影响满足瑞利阻尼模型规律。

(2)文中板单元模型各阶模态阻尼比(钢材)约为0.2%～0.3%，复合材料的阻尼性能要优越于钢板，玻璃钢(E800/350环氧树脂)的阻尼比约为钢板的4倍左右。由于复合材料结构的阻尼大，模态密集度高、叠加效应明显，一般分析方法易于产生较大的识别误差，更有必要对试验估算的阻尼比进行修正。

因此，这种从数值计算实现叠加模态分离的角度来提高阻尼比测试精度的方法，有助于更准确地探究不同材料、结构的阻尼性能，为实际工程结构的模态参数识别理论发展提供了新思路。

[ 1 ] 郭雪莲,范雨,李琳. 航空发动机叶片高频模态阻尼的实验测试方法[J]. 航空动力学报, 2014, 29(9): 2014-2112. GUO Xuelian, FAN Yu, LI Lin. Experimental test method for high-frequency modal damping of turbo machinery blades [J]. Journal of Aerospace Power, 2014, 29(9): 2014-2112.

[ 2 ] YIN F, OHSAWA Y, SATO A,et al. Characterization of the strain-amplitude and frequency dependent damping capacity in the M2052 alloy [J]. Materials Transactions, 2001, 42(3): 385-388.

[ 3 ] 郑成琪,程晓农. 金属阻尼性能测试方法的现状与发展[J]. 实验力学, 2004, 19(2): 248-256. ZHENG Chengqi, CHENG Xiaonong. Present status and future of damping measurement for metals[J]. Journal of Experimental Mechanics, 2004, 19(2): 248-256.

[ 4 ] SILVA C W.振动阻尼、控制和设计[M]. 北京:机械工业出版社,2013:8-9.

[ 5 ] 戴德沛.阻尼减振降噪技术[M].西安:西安交通大学出版社,1986:74-75.

[ 6 ] 黄方林,何旭辉，陈政清,等. 识别结构模态阻尼比的一种新方法[J]. 土木工程学报, 2002, 36(6): 20-23. HUANG Fanglin, HE Xuhui, CHEN Zhengqing, et al. A new approach for identification of modal damping ratios for structure [J]. China Civil Engineering Journal, 2002, 36(6): 20-23.

[ 7 ] 陈奎孚,焦群英. 半功率点法估计阻尼比的误差分析[J]. 机械强度, 2002, 24(4): 510-514. CHEN Kuifu, JIAO Qunying. Influence of linear interpolation approximation to half power points on the damping estimation precision [J]. Journal of Mechanical Strength, 2002, 24(4): 510-514.

[ 8 ] 陈奎孚,张森文. 半功率点法估计阻尼的一种改进[J]. 振动工程学报, 2002, 15(2): 151-155. CHEN Kuifu, ZHANG Senwen. Improvement on the damping estimation by half power point method [J]. Journal of Vibration Engineering, 2002, 15(2): 151-155.

[ 9 ] 应怀樵,刘进明,沈松. 半功率带宽法与INV阻尼计法求阻尼比的研究[J]. 噪声与振动控制, 2006, 26(2): 4-6. YING Huaiqiao, LIU Jinming, SHEN Song. Half-power bandwidth method and INV damping ration solver study [J]. Noise and Vibration Control, 2006, 26(2): 4-6.

[10] BROWN D L, ALLEMANG R J, ZIMMERMAN R D,et al. Parameter estimation techniques for modal analysis [R]. Sae Paper,1979,88(2):299-305.

[11] 孟凡通. 基于模糊聚类的密集模态参数识别方法研究及实现[D]. 秦皇岛: 燕山大学, 2012.

[12] 刘绍奎,韩增尧. 基于Gauss滤波和Hilbert变换的模态阻尼辨识方法[J]. 强度与环境, 2008, 35(1): 29-34. LIU Shaokui, HAN Zengyao. Modal damping parameters identification based on Gauss filter and Hilbert transform [J]. Structure and Environment Engineering, 2008, 35(1): 29-34.

[13] 尹帮辉,王敏庆,吴晓东. 结构振动阻尼测试的衰减法研究[J]. 振动与冲击, 2014, 33(4): 100-106. YIN Banghui, WANG Minqing, WU Xiaodong. Decay method for measuring structural vibration damping [J]. Journal of Vibration and Shock, 2014, 33(4): 100-106.

[14] 申建红,李春祥,李锦华. 基于解析小波变换识别结构的模态阻尼参数[J]. 振动与冲击, 2009, 28(10): 89-93. SHEN Jianhong, LI Chunxiang, LI Jinhua. Identifying structural modal damping parameters based on analytic wavelet transformation [J]. Journal of Vibration and Shock, 2009, 28(10): 89-93.

[15] WANG B T CHENG D K. Modal analysis of mdof system by using free vibration response data only [J]. Journal of Sound and Vibration, 2008, 311(3/4/5): 737-755.

[16] 陈茉莉,李舜酩. 基于分布激励突卸的转子叶片阻尼比试验[J]. 航空动力学报, 2009, 24(11): 2521-2526. CHEN Moli, LI Shunming. Damping ratio experiment study on rotary blade based on distributing excitation unloaded instantaneously [J]. Journal of Aerospace Power, 2009, 24(11): 2521-2526.

[17] 淡丹辉,孙利民. 结构动力有限元的模态阻尼比单元阻尼建模法[J]. 振动、测试与诊断, 2008, 28(2): 100-103. DAN Danhui, SUN Limin. Damping modeling and its evaluation based on dynamical analysis of engineering structure by finite element method [J]. Journal of Vibration, Measurement and Diagnosis, 2008, 28(2): 100-103.

[18] 李德葆,陆秋海. 实验模态分析及其应用[M]. 北京: 科学出版社, 2001: 58-67.

[19] 黄应来,董大伟,闫兵. 密集模态分离及其参数识别方法研究[J].机械强度,2009,31(1):8-13. HUANG Yinglai, DONG Dawei, YAN Bing. Study on closely spaced modes decomposition and modal parameter identification[J]. Journal of Mechanical Strength, 2009, 31(1): 8-13.

[20] 温金鹏,杨智春,李斌,等. 材料阻尼测试方法研究[J]. 振动、测试与诊断, 2008, 28(3): 220-224. WEN Jinpeng, YANG Zhichun, LI Bin, et al. A method for material damping measurement [J]. Journal of Vibration, Measurement and Diagnosis, 2008, 28(3): 220-224.

[21] 克拉夫R,彭津J. 结构动力学[M]. 北京:高等教育出版社,2006:184-185.

A method based on numeral calculation and experiment for determination of modal damping

TANGYuhang1，CHENZhijian1，MEIZhiyuan1，SUNJianlian2

(1.Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China; 2. State Grid Bengbu Power Supply Company, Bengbu 233000, China)

Any distribution of incentives lead to multiple modes of response, it is thus very difficult to stimulate single mode of vibration in experiments. The limitation of current signal processing techniques implies that traditional methods used to estimate the damping ratio cannot effectively separate the superposition modes, which leads to larger error in obtained damping ratio. Starting with modal superposition method theory in dealing with multiple-degrees-of-freedom system dynamic response, it was pointed out that mode confusion problem is one important limitation in precise damping ratio test. Modes are more crowded and the superimposed effect is more significant when system damping is larger and stiffness is lower. One program was proposed to achieve “pure mode” extraction by applying modal truncation in numeral calculation. The formula expressions of frequency-response spectrum peak line in both of resonance excitation experiment and numeral calculation were derived. The relationship between them was investigated. “Pure mode” calculation results were used to correct experimental damping ratio. Through four different board units, eight pre-order experimental modal analysis and numerical calculation parameter correction, combining frequency response function to verify data reliability of the correction damping ratio, some laws of damping ratio between different structures or materials were obtained. The results show that: the identification accuracy of composite plate’s modal damping ratio is lower than steel’s by model experiment calculation, and its damping performance is often underestimated and large amplitude correction are also often needed. The method provides a guideline for further study of modal parameter identification.

numeral calculation；modal damping ratio identification; frequency response curve; modal truncation; modal superposition

国家自然科学基金(51479205)

2016-04-19 修改稿收到日期：2016-07-20

唐宇航 男，博士，1991年生

陈志坚 男，教授，1957年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.04.006