柱形波纹压溃元件轴向冲击力学行为研究

付本元，廖昌荣，李祝强，章 鹏，简晓春，吴春江

(1.重庆大学 光电技术及系统教育部重点实验室智能结构中心,重庆 400044; 2.重庆交通大学 交通运输学院,重庆 400074)

柱形波纹压溃元件轴向冲击力学行为研究

付本元1，廖昌荣1，李祝强1，章 鹏1，简晓春2，吴春江2

(1.重庆大学 光电技术及系统教育部重点实验室智能结构中心,重庆 400044; 2.重庆交通大学 交通运输学院,重庆 400074)

针对冲击载荷作用下多层柱形波纹压溃元件的力学特性分析非常困难的问题，结合柱形波纹压溃元件的冲击压溃变形特征，将柱形波纹压溃元件的变形划分为弹性变形阶段、壁面接触前的塑性变形阶段、混合塑性变形阶段、壁面接触过程中的塑性变形阶段，研究了轴向冲击下柱形波纹压溃元件变形抗力的理论计算方法。利用Matlab Simulink软件编程，计算分析了不同高度落锤冲击柱形波纹压溃元件产生的变形抗力与压溃量之间的映射特性，并与实验结果进行了比较。研究结果表明,在不同跌落高度冲击下，理论计算的变形抗力与实验结果吻合较好，证明所提出的理论分析方法是合理的，对波纹压溃缓冲元件的工程应用具有指导意义。

波纹压溃元件;冲击载荷;变形抗力;应变强化效应;应变率硬化效应

在机械碰撞过程中，合理利用缓冲装置的抗冲特性对吸收冲击能量、改善碰撞物加速度时间历程、降低物品损伤具有重要的作用。由于承受轴向冲击载荷具有良好的吸能特征和较大的压溃变形量，柱形波纹压溃元件在缓冲领域的应用受到国内外学者的高度关注。SINGACE等[1]实验研究了管状波纹压溃元件的轴向压溃能量吸收特性，结果表明该元件具备理想的吸能特性；HOSSEINIPOUR等[2]通过改变壁厚和冲击速度，实验研究了波纹管状压溃元件的力学行为；EYVAZIAN等[3]研究了柱形波纹压溃元件的压溃特性、能量吸收以及失效模式，结果表明在轴向载荷下带有波纹的圆管失效模式是可预测和控制的；王晓等[4]对柱形波纹压溃元件的碰撞性能进行了实验研究，结果表明柱形波纹压溃元件的吸能曲线比较平稳，可制作汽车碰撞吸能部件；张平等[5]针对柱形波纹压溃元件耐撞性进行多目标优化，由于充分考虑到结构内径、波高、波距、管壁半径、波纹角以及波纹段的壁厚等几何参数的离散化、规格化特征，因而优化结果更加贴近实际工程问题的要求；MAMALIS等[6]通过数值模拟方法对带环形沟槽波纹压溃元件进行研究，数值结果与实验结果吻合较好；GALIB等[7]使用非线性有限元方法对轴向压缩载荷下圆形铝管的压溃特性进行研究，数值预测压溃力以及褶皱特征与实验结果一致；ZHANG等[8]通过LS-DYNA对多边形波纹柱进行压溃分析，得出多边形波纹柱可用以防撞性结构设计；谭丽辉等[9-10]在柱形波纹压溃元件的圆形截面上分别设置圆弧形诱导凹槽、凸槽和凸凹交替的诱导槽，采用非线性有限元软件 LS-DYNA 得到不同几何参数模型的碰撞响应及其对抗撞性的影响；郝文乾等[11-12]通过LS-DYNA有限元软件建立了轴向冲击载荷作用下薄壁波纹压溃元件的有限元模型，得出影响波纹压溃元件变形的两个主要参数是冲击速度和径厚比；贾志刚等[13]利用轴对称模型分析了多层U型波纹压溃元件在内压及轴向位移作用下的应力分布及层间的相互作用；杨义俊等[14]建立了两层波纹管的非线性有限元模型，计算了两层波纹管在受内压和轴向位移荷载及两者共同作用下波纹管的应力分布；王帅等[15]利用ANSYS程序接触有限元方法对4层U型波纹管轴向刚度的线性和非线性特性进行了研究。与单层波纹管状压溃元件相比，多层波纹管状压溃元件在冲击载荷作用下，其力学行为更加复杂，一般采用实验方法和数值仿真软件研究其冲击动力学行为，系统的理论分析模型还不够完备，现有的理论方法还不能指导波纹柱形压溃元件的设计。因此，从理论上探讨在冲击载荷作用下波纹压溃元件的抗冲击特性，对波纹压溃缓冲元件的工程应用具有重要的价值。

1 柱形波纹压溃元件的结构与材料特性

本文采用柱形多层波纹压溃元件作为研究对象，压溃元件材料为304不锈钢，波纹设计为U形波，柱形波纹压溃元件的基本结构参数如图1所示。Ri为柱形波纹压溃元件直边段内径，Ro为柱形波纹压溃元件波峰处外径，hb为波高，wd为波距，ri为波谷半径，ro为波峰半径，δ为柱形波纹压溃元件单层名义厚度，N为波数。

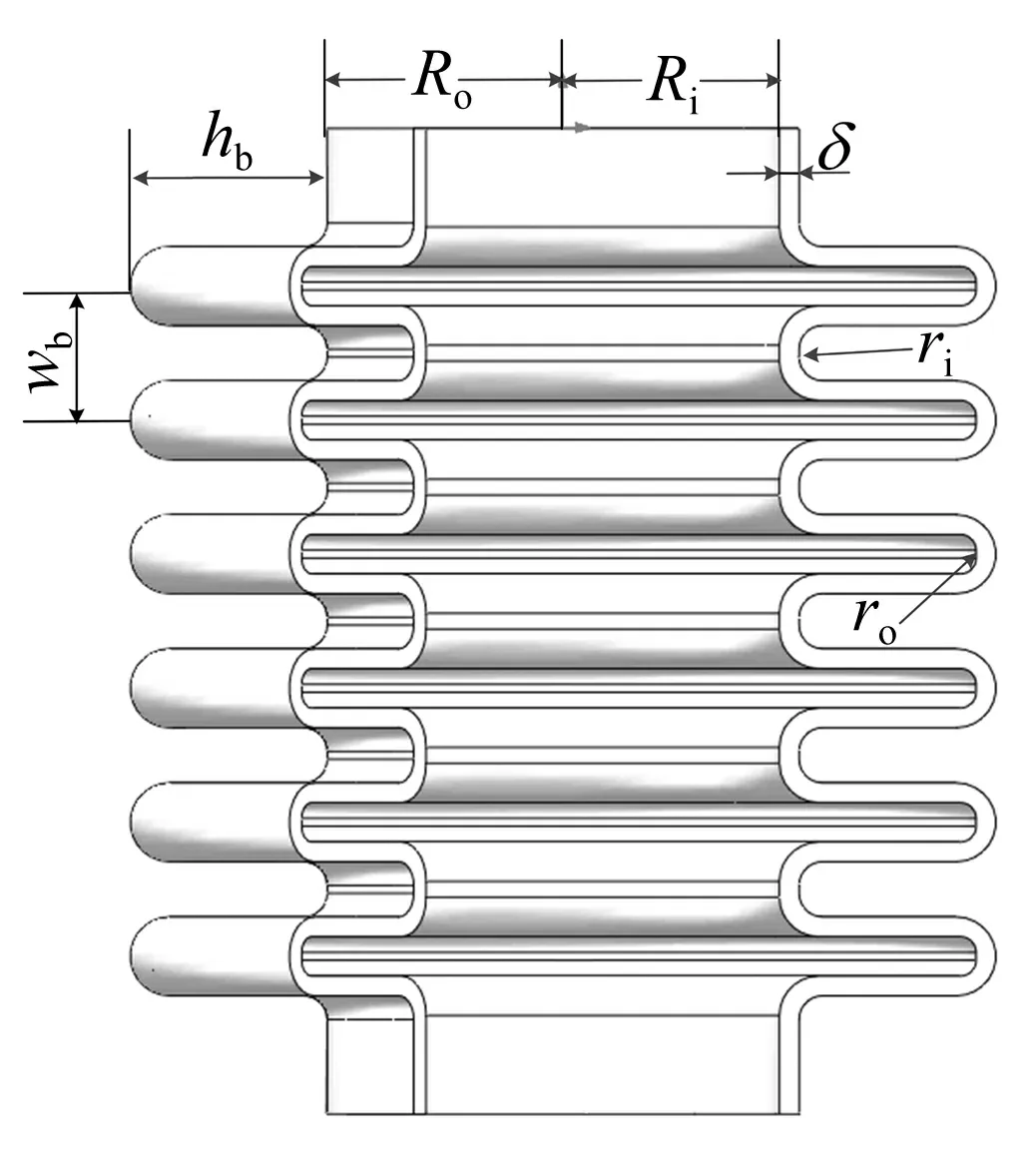
图1 柱形波纹压溃元件的结构示意图Fig.1 The diagram of crushable cylindrical-corrugated component structure

在静载荷或者缓慢载荷作用下，应力σ主要受应变ε的影响，即应变强化效应。304不锈钢材料在压缩时的变形可以分为弹性变形阶段与塑性变形阶段，压缩变形时应力-应变模型可以用分段函数来表示

(1)

式中:ε为材料的应变;E为弹性模量;G为材料塑性应变常数;n为材料的塑性应变指数;δ0.2为名义屈服极限;ε0.2为产生名义屈服极限δ0.2时材料的应变。

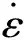
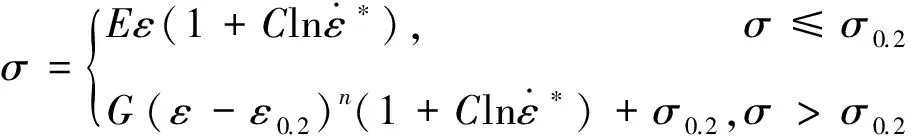
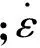
2 柱形波纹压溃元件的轴向压溃力学行为

波纹压溃元件受到轴向冲击载荷作用下，引起的压溃变形分四个阶段，如图2所示，分别表示为：①弹性变形阶段；②材料的应力达到屈服强度，进入壁面接触前的塑性变形阶段；③继续压缩波峰或波谷中半径较小的开口壁面开始接触，波峰或波谷中半径较小的变形发生壁面接触过程中的塑性变形，半径较大的变形依然为壁面接触前的塑性变形，这一阶段为混合塑性变形阶段；④波峰或波谷中半径较大的开口壁面开始接触，此时波纹压溃元件变形进入到壁面接触过程中的塑性变形阶段。

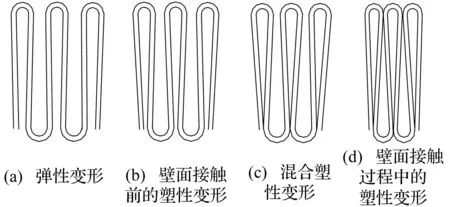
图2 波纹压溃元件压溃变形过程Fig.2 The deformation process of crushable cylindrical-corrugated component

2.1 弹性变形阶段的力学行为

2.1.1 变形刚度

使用工程近似法Kellogg法[16]计算，静压下波纹压溃元件弹性变形阶段的整体轴向刚度

(3)

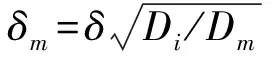
在冲击环境中，波纹压溃元件的轴向刚度还应考虑应变率硬化效应，冲击载荷作用下波纹压溃元件弹性变形阶段的整体轴向刚度计算式

(4)

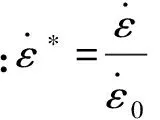
2.1.2 最大压溃量

根据Kellogg法，在弹性变形阶段单波轴向位移载荷引起的经向弯曲应力为

(5)

式中:et为波纹压溃元件单波轴向位移。

在冲击环境中，波纹压溃元件的经向弯曲应力也应考虑应变率硬化效应的影响，冲击载荷作用下波纹压溃元件在弹性变形阶段单波轴向位移引起的经向弯曲应力为

(6)

冲击过程中随波纹压溃元件的压溃量增大，弹性变形阶段的极限位移对应的波纹压溃元件径向弯曲应力为材料的屈服应力

σd max=σ0.2

(7)

由式(6)和式(7)可得

(8)

波纹压溃元件在弹性变形阶段最大的压溃量为

xt max=Net max

(9)

2.1.3 变形抗力与压溃量

波纹压溃元件在受到冲击后压缩变形，其变形抗力与压溃量的关系服从胡克定律

Ft(x)=Kd·x

(10)

式中:Ft为弹性变形阶段的变形抗力；x为波纹压溃元件的压溃量。

2.2 壁面接触前塑性变形阶段的力学行为

冲击过程中，波纹压溃元件的波峰与波谷开口逐渐闭合，如图2所示，波纹压溃元件受到冲击力作用，壁面会逐渐倾斜。壁面接触前的塑性变形如图2(b)所示，发生于弹性变形之后且在波峰或波谷中半径较小的开口壁面接触之前。

将波纹压溃元件等效为圆筒，冲击过程中在弹性变形阶段的应力-应变关系为

(11)

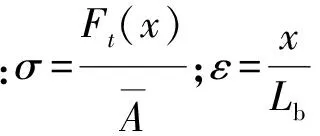
(12)

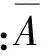
由式(4)、式(10)、式(12)联立可求得等效直圆筒的横截面积为

(13)

由式(2)可知，塑性变形阶段波纹管的应力-应变的关系用幂函数来描述如下

(14)

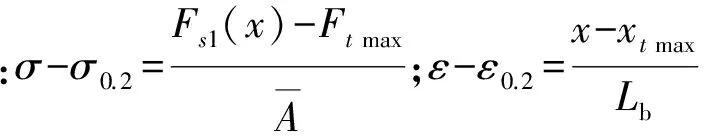
(15)

式中，Ft max为波纹压溃元件在弹性变形阶段的最大抗力。

故壁面接触前塑性变形的最大压溃发生于波峰或波谷中半径较小的开口壁面刚好接触的位置，考虑到应变率硬化效应的影响，这个阶段的最大压溃量为

(16)

其中，

rmin=min{ri,ro}

(17)

式中，ξ为壁面倾斜修正系数，其值通过实验确定。

2.3 混合塑性变形阶段力学行为

在波峰或波谷中半径较小的开口闭合之后发生壁面接触后的塑性变形，而波峰或波谷中半径较大的则继续产生壁面接触前的塑性变形，直到全部开口闭合，这一过程的变形为混合塑性变形。在这一阶段既存在壁面接触前的塑性变形又存在壁面接触过程中的塑性变形，其变形抗力为壁面接触前塑性变形的抗力与壁面接触过程中塑性变形阶段抗力的线性组合，变形抗力为

Fs2(x)=bmax·Fs1(x)+bmin·Fs3(x)

(18)

其中，

(19)

(20)

rmax=max{ri,ro}

(21)

式中:bmin、bmax为线性组合系数；Fs3(x)为壁面接触后塑性变形抗力的形式。

混合塑性变形阶段的压溃量最大的时候正是波峰或波谷中半径较大的开口壁面刚刚接触的位置，同时考虑到应变率硬化效应的影响，因此混合塑性变形阶段的最大压溃量为

(22)

2.4 壁面接触过程中塑性变形阶段力学行为

波纹压溃元件开口壁面接触后，将半波等效成梁ba、bc。由图3所示，c点为移动点，即在作用力ΔF的作用下，c点向左沿水平方向移动。ba是悬臂梁，a端固定，b点绕固定端a转动。b处的挠度方程为

(23)

其中，

ΔF=Fs3-Fs1_max

(24)

(25)

式中:Fs3为壁面接触过程中的抗力;Fs1_max为壁面接触前的最大抗力；θ为梁ba与水平方向的夹角；I为梁的惯性矩。

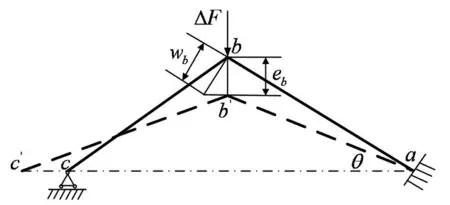
图3 壁面接触过程中的简化模型Fig.3 The simplified model of plastic deformation during surface contact

以下是波峰或波谷中半径较小的波纹在壁面接触过程中变形抗力计算过程，半径较大的波纹同理。由于夹角θ比较小，则cosθ≈1，悬臂梁ba的长度近似看作为波纹半径rmin，b点处的挠度可由式(23)变为

(26)

假设在此过程中波纹压溃元件的轴向位移为Δx，则Δx与wb的关系为

(27)

联立式(25)～式(27)，并考虑到应变率硬化效应的影响，可得作用力与轴向位移的关系为

(28)

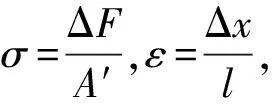
(29)

联立式(28)式(29)，可得壁面接触过程中直圆筒的等效横截面积为

(30)

其中，

l=Lb-xs1_max

(31)

Δx=x-xs1_max

(32)

式中，l为开口壁面刚接触时波纹压溃元件波纹段的长度。

冲击载荷作用下壁面接触过程中的弹性变形量很小，可以忽略。则壁面接触过程中波纹压溃元件直接进入塑性变形阶段，其应力-应变关系为

(33)

联立式(24)、式(30)和式(33)，整理后可得波纹压溃元件在壁面接触过程中的变形抗力

(x-xs1_max)n+Fs1_max

(34)

式中，Fs1_max为壁面接触前的塑性变形的最大压溃量对应的抗力。

3 冲击实验及结果分析

3.1 冲击试验台的搭建

为了研究波纹压溃元件在冲击载荷作用下的力学特性，本文搭建了落锤式冲击试验平台，该平台主要由落锤式冲击试验机、传感系统以及数据采集系统等部分组成，如图4所示。

1-数据处理计算机;2-电荷放大器;3-数据采集卡;4-落锤;5-提升系统;6-波纹压溃元件;7-激光位移传感器;8-压电式力传感器图4 冲击试验台Fig.4 Drop tower facility

落锤式冲击试验平台的工作原理如图5所示，提升系统将落锤提升到一定高度，然后由落锤自由落体运动获得波纹压溃元件较高的冲击速度和较大的冲击力，冲击速度的大小可通过落锤提升的高度调节。实验过程中，落锤的冲击头与波纹压溃元件接触后高速压溃波纹压溃元件，压电式力传感器、激光位移传感器分别记录冲击过程中波纹压溃元件的变形抗力和压溃量。实验分别记录了在不同跌落高度下波纹压溃元件的变形抗力、压溃量，实验条件如表1所示。

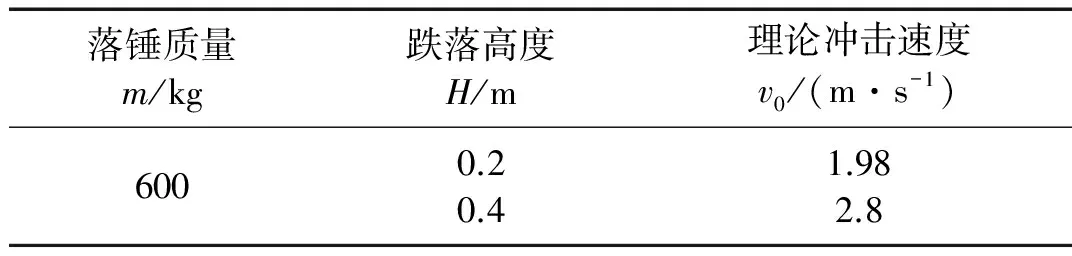
表1 实验测试条件

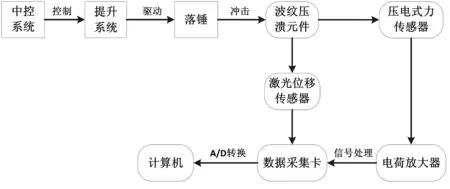
图5 试验平台工作原理Fig.5 The working principle of test platform

3.2 波纹压溃元件结构尺寸选择

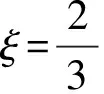
表2 波纹压溃元件的结构尺寸

图6 波纹压溃体实物图Fig.6 Physical maps of crushable cylindrical-corrugated component

3.3 冲击仿真计算

基于此冲击试验平台，本论文使用Matlab R2013a所提供的Simulink仿真模拟器进行了落锤冲击仿真实验，仿真实验中用Matlab Function将上述理论公式以图7所示的逻辑关系编辑后嵌入仿真框图中，分别对波纹压溃元件进行了0.2 m、0.4 m高度冲击仿真实验。

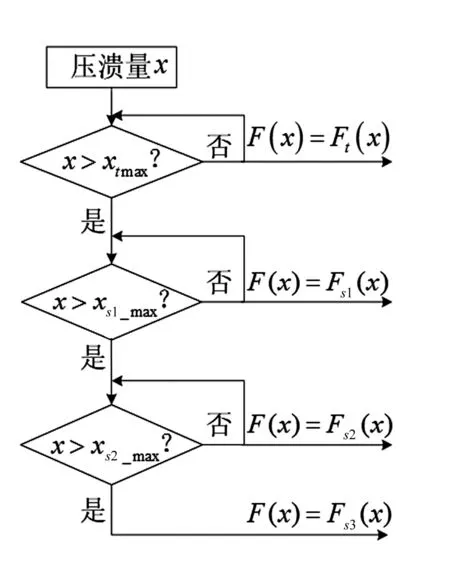
图7 Matlab Function逻辑关系Fig.7 Logical relations of Matlab Function

3.4 实验结果及分析

图8、图9分别给出了理论仿真与实验在不同高度冲击时波纹压溃元件的变形抗力随压溃量变化情况。从两图均可以看出，落锤在0.4 m高度跌落时波纹压溃元件的压溃量>0.2 m高度跌落时的压溃量，这是由于落锤在0.4 m跌落时的重力势能比0.2 m跌落时大，波纹压溃元件需要更大的压溃变形量来吸收落锤的的重力势能。压溃量在36 mm之前，同一压溃量下不同高度跌落时的变形抗力基本一致，说明这一过程的变形抗力主要受应变强化效应影响。压溃量在36 mm之后，同一压溃量下0.4 m跌落时波纹压溃元件的变形抗力>0.2 m跌落时的变形抗力，说明在这一过程中变形抗力除了受应变强化效应影响之外，受应变率硬化效应的影响也十分明显。另外，由于0.4 m高度跌落时波纹压溃元件的应变率>0.2 m高度跌落时的应变率，因此落锤在0.4 m跌落比0.2 m跌落时使波纹压溃元件更早进入到混合塑性变形阶段。

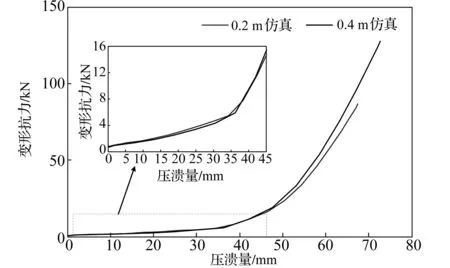
图8 不同高度冲击时变形抗力-压溃量仿真曲线Fig.8 Simulated curves of deformation resistance-crushed displacement under different drop heights

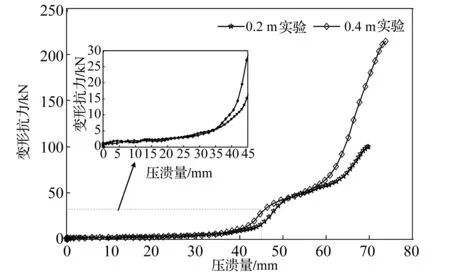
图9 不同高度冲击时变形抗力-压溃量实验曲线Fig.9 Experimental curves of deformation resistance-crushed displacement under different drop heights

图10所示为落锤在0.2 m跌落时波纹压溃元件变形抗力-压溃量曲线的理论仿真与实验数据的对比情况。由图10可知，在压溃量44.5 mm之前的理论仿真与实验数据曲线吻合度非常好，这一过程主要是波纹压溃元件的弹性变形与壁面接触前的塑性变形阶段，由此可知弹性变形与壁面接触前的塑性变形阶段对波纹压溃元件的变形抗力理论分析非常符合实际情况。波纹压溃元件的压溃量在44.5～61.2 mm，这一过程主要处于混合塑性变形阶段，理论仿真与实验数据中的变形抗力随压溃量均出现迅速增大的现象，由此可知壁面接触过程中塑性变形的变形抗力远比壁面接触前的变形抗力大；另外在这一阶段理论仿真曲线与实验数据形状差异非常大，实验数据中的变形抗力-压溃量曲线呈现“半凸台”状，理论仿真中的变形抗力-压溃量曲线呈现“半凹槽”状，这是由于在混合塑性变形阶段不仅是应变强化效应与应变率硬化效应对变形抗力产生影响，波纹压溃元件层间摩擦力在混合塑性变形阶段对变形抗力也产生很大的影响，导致实验数据中变形抗力-压溃量曲线的斜率更大，呈现“半凸台”状。压溃量在61.2 mm之后，波纹压溃元件的变形形式表现为壁面接触过程中的塑性变形，这一阶段的理论仿真变形抗力-压溃量曲线的斜率比实验数据的斜率稍小，因此随着压溃量的增大理论仿真中的变形抗力由一开始的略大于实验数据中的抗力逐渐变为略小于实验数据中的变形抗力，但整个过程中理论仿真与实验数据中的变形抗力基本一致。

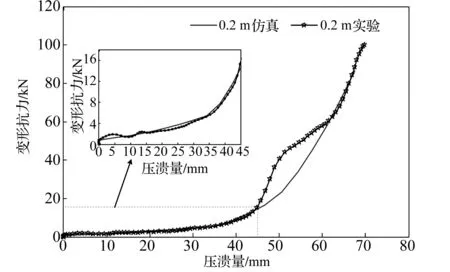
图10 0.2 m高度冲击下理论仿真与实验数据对比Fig.10 Comparation of the theoretical values and experimental result with drop height of 0.2 m

图11为落锤在0.4 m跌落时波纹压溃元件的抗力-压溃量曲线的理论仿真与实验数据的对比情况。由图11可知，在压溃量为41.2 mm之前，即在弹性变形与壁面接触前的塑性变形阶段，理论仿真与实验数据吻合非常好。压溃量在41.2～61.5 mm，波纹压溃元件主要表现为混合塑性变形，在这一阶段由于层间摩擦力的存在导致实验数据的变形抗力-压溃量曲线依然表现为“半凸台”状，而理论仿真由于未考虑这一因素，其变形抗力-压溃量曲线表现为“半凹槽”状。压溃量超过61.5 mm之后为壁面接触过程中的塑性变形，理论仿真中的变形抗力-压溃量曲线斜率大于实验数据，理论仿真中的变形抗力比实验数据中的小很多，出现这种现象的原因可能两种：①理论仿真未考虑层间摩擦力的影响；②波纹压溃元件的应力与应变率硬化效应不是呈线性关系，而是一种幂函数关系。

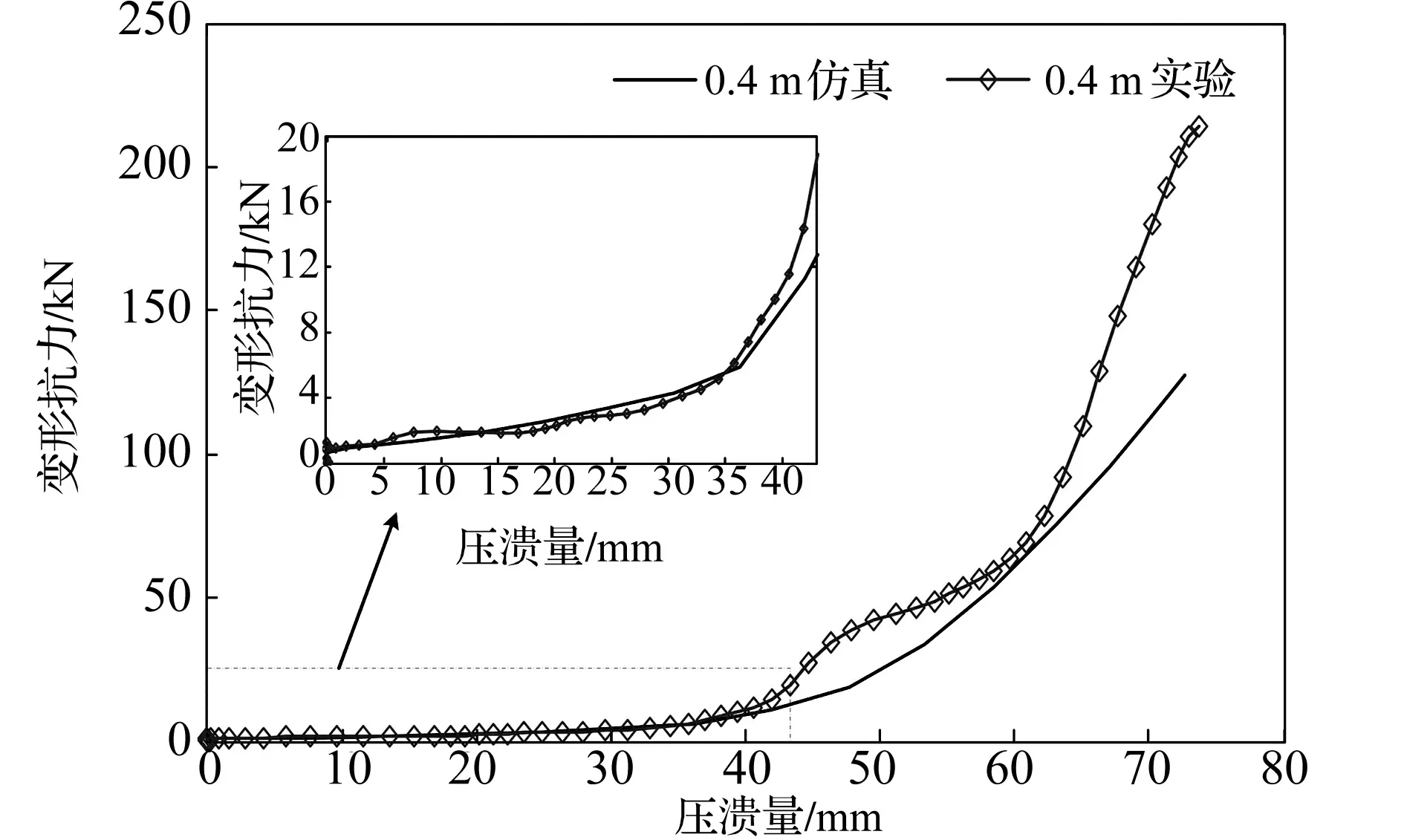
图11 0.4 m高度冲击下理论仿真与实验数据对比Fig.11 Comparation of the theoretical values and experimental result with drop height of 0.4 m

4 结 论

本文从理论上研究了在轴向冲击载荷作用下柱形波纹压溃元件的力学行为，将柱形波纹压溃元件在冲击过程中的变形划分为弹性变形阶段、壁面接触前的塑性变形阶段、混合塑性变形阶段、壁面接触过程中的塑性变形阶段。理论仿真计算了落锤在不同高度跌落时柱形波纹压溃元件的变形抗力随压溃量的变化情况，并与实验结果进行了比较。

(1) 在弹性变形阶段与壁面接触前的塑性变形阶段理论计算与实验结果非常吻合，充分说明柱形波纹压溃元件变形抗力的理论分析在这两个阶段非常符合实际情况。

(2) 混合塑性变形阶段理论仿真计算的抗力-压溃量曲线呈现“半凹槽”状，实验中抗力-压溃量曲线呈现“半凸台”状，是因为理论计算中没有考虑波纹压溃元件层间摩擦对变形抗力的影响，导致在这一变形过程中误差较大。

(3) 在壁面接触过程中的塑性变形阶段，落锤在0.2 m高度跌落时理论仿真计算与实验结果吻合度非常好，但是落锤在0.4 m高度跌落时理论计算的变形抗力小于实验结果的变形抗力，这是由于理论计算未考虑波纹压溃元件层间摩擦力以及波纹压溃元件的应力与应变率硬化效应的关系呈非线性所致。

(4) 本文对柱形波纹压溃元件的变形抗力分析与实验结果基本吻合，但为了使理论抗力更加符合实际情况，接下来应该改善应变率硬化效应对力学模型的影响并考虑层间摩擦力的作用。

[ 1 ] SINGACE A A, EL-SOBKY H. Behaviour of axially crushed corrugated tubes[J]. International Journal of Mechanical Sciences, 1997, 39(3):249-268.

[ 2 ] HOSSEINIPOUR S J, DANESHI G H. Energy absorbtion and mean crushing load of thin-walled grooved tubes under axial compression[J]. Thin-Walled Structures, 2003, 41(1):31-46.

[ 3 ] EYVAZIAN A, HABIBI M K, HAMOUDA A M, et al. Axial crushing behavior and energy absorption efficiency of corrugated tubes[J]. Materials & Design, 2013, 54(2):1028-1038.

[ 4 ] 王晓, 刘星荣. 波纹管碰撞性能的试验研究[J].中国公路学报, 2001, 14(4):106-109. WANG Xiao, LIU Xingrong. Experiment study of the absorbing energy of corrugated tube [J]. China Journal of Highway and Transport, 2001, 14(4): 106-109.

[ 5 ] 张平, 马建, 那景新. 波纹管耐撞性的多目标优化[J]. 振动与冲击, 2015, 34(15):12-16. ZHANG Ping, MA Jian, NA Jingxin. Multi-objective optimization for crashworthiness of corrugated tubes [J]. Journal of Vibration and Shock, 2015, 34(15):12-16.

[ 6 ] MAMALIS A G, MANOLAKOS D E, IOANNIDIS M B, et al. Numerical modelling of the axial plastic collapse of externally grooved steel thin-walled tubes[J]. International Journal of Crashworthiness, 2003, 8(6):583-590.

[ 7 ] GALIB D A, LIMAM A. Experimental and numerical investigation of static and dynamic axial crushing of circular aluminum tubes[J]. Thin-Walled Structures, 2004, 42(8):1103-1137.

[ 8 ] ZHANG X, HUH H. Crushing analysis of polygonal columns and angle elements[J]. International Journal of Impact Engineering, 2010, 37(4):441-451.

[ 9 ] 谭丽辉, 徐涛, 张炜,等. 带有圆弧形凸槽金属薄壁圆管抗撞性优化设计[J]. 振动与冲击, 2013, 32(21):80-84. TAN Lihui, XU Tao, ZHANG Wei, et al. Crashworthiness optimization design for a metal thin-walled tube with convex grooves [J]. Journal of Vibration and Shock, 2013, 32(21):80-84.

[10] 谭丽辉, 谭洪武, 毛志强,等. 具有不同诱导槽结构的薄壁圆管抗撞性优化[J]. 振动与冲击, 2014,33(8):16-21. TAN Lihui, TAN Hongwu, MAO Zhiqiang et al.Crashworthiness design optimization of thin-walled cylinders with different inducing grooves [J]. Journal of Vibration and Shock,2014,33(8):16-21.

[11] 郝文乾.轴向冲击载荷下薄壁折纹管和波纹管的屈曲与能量吸收[D].太原:太原理工大学,2014.

[12] LIU Z, HAO W, XIE J, et al. Axial-impact buckling modes and energy absorption properties of thin-walled corrugated tubes with sinusoidal patterns[J]. Thin-Walled Structures, 2015, 94:410-423.

[13] 贾志刚, 寿比南, 梅林涛. 有限元方法在膨胀节强度分析中的应用[J]. 压力容器, 2001, 18(4):43-45. JIA Zhigang, SHOU Binan, MEI Lintao. Application of FEM to the analysis of the structure strength of expansion joints [J]. Pressure Vessel Technology,2001,18(4):43-45.

[14] 杨义俊, 王心丰. 多层波纹管非线性有限元应力分析[J]. 压力容器, 2003, 20(9): 13-16. YANG Yijun, WANG Xinfeng. Nonlinear finite element analysis of the multiply bellows [J]. Pressure Vessel Technology, 2003, 20(9): 13-16.

[15] 王帅, 王建军. 考虑层间摩擦的多层波纹管轴向刚度非线性有限元分析[J]. 压力容器, 2007, 24(12):12-15. WANG Shuai, WANG Jianjun. Nonlinear finite element analysis of multilayer bellows’ axial stiffness considering the influence of inter-layer friction [J]. Pressure Vessel Technology, 2007, 24(12):12-15.

[16] 李永生. 波形膨胀节实用技术[M]. 北京:化学工业出版社, 2000.

[17] ABRAMOWICZ W, JONES N. Dynamic axial crushing of circular tubes[J]. International Journal of Impact Engineering, 1984, 2(3):263-281.

[18] 李星星. 304不锈钢本构模型参数识别研究[D]. 武汉:华中科技大学,2012.

A study on the mechanical behavior of a crushable cylindrical corrugated component under axial impact

FUBenyuan1,LIAOChangrong1,LIZhuqiang1,ZHANGPeng1,JIANXiaochun2,WUChunjiang2

(1. Key Laboratory for Optoelectronic Technology and Systems, College of Optoelectronic Engineering, Chongqing University, Chongqing 400044, China; 2. Transportation Institute, Chongqing Jiaotong University, Chongqing 400074, China)

Analyzing the mechanical behavior of a crushable multi-cylindrical-corrugated component under impact load is currently a challenge. This paper presents a theoretical methodology for evaluation of the deformation resistance of a crushable cylindrical-corrugated component under axial impact load. By investigating the collapse deformation characteristics, the deformation was divided into four sections: elastic deformation stage, plastic deformation stage before surface contact, mixed plastic deformation stage, and plastic deformation stage during surface contact. The theoretical mapping relationship between the deformation resistance and crushed displacement under different drop heights was obtained by Matlab Simulink. The theoretical relationship was compared with the experimental result, which showed a good agreement between the predicted resistant forces and the testing data under various drop heights. The result shows the feasibility of the proposed analytical methodology for the practical application of the crushable cylindrical-corrugated component.

crushable cylindrical-corrugated component; impact load; deformation resistance; strain-strengthening effect; strain rate hardening effect

国家自然科学基金面上项目(51575065);中央高校基本科研业务费项目(106112015CDJZR125517)

2015-09-14 修改稿收到日期：2016-01-12

付本元 男，博士，1986年生

廖昌荣 男，博士后，教授，1966年生 E-mail：crliao@cqu.edu.cn

O347.3

A

10.13465/j.cnki.jvs.2017.04.004