高速车铣加工三维颤振的稳定性分析与试验研究

2017-03-09关跃奇魏克湘张文明关汗青

振动与冲击 2017年4期

关跃奇，魏克湘，2，张文明，关汗青

(1.湖南工程学院机械工程学院，湖南湘潭 411101； 2. 湖南省风电装备与电能变换协同创新中心，湖南湘潭 411101; 3.上海交通大学机械系统与振动国家重点实验室，上海 200240; 4.湖南大学机械与运载工程学院，长沙 410082)

关跃奇1，魏克湘1，2，张文明3，关汗青4

针对立铣刀高速车铣加工，基于其切削原理采用解析法建立三维颤振稳定域的理论模型。在立铣刀四轴车铣加工模态试验基础上，仿真分析了颤振稳定域叶瓣图，结果表明立铣刀高速车铣加工产生颤振的条件与铣刀几何形状、工件材料、铣刀转速、切削深度和机床结构的频率响应函数等密切相关。在进行车铣切削颤振稳定域试验时，其切削力频谱分析的结果表明：当刀齿切入频率起主导作用时，切削过程是无颤振和稳定的；当系统模态频率起主导作用时，将产生颤振并测得切削力和表面粗糙度值都大于或高于无颤振情况。因此该理论模型及仿真结果对立铣刀车铣加工零件的加工效率和加工精度可提供相应的理论指导。

立铣刀；高速车铣；颤振稳定性；建模

与传统车削相比，四轴车铣因使用了立铣刀等多刃刀具进行间断切削，无论加工何种材料的零件都能容易实现自动断屑、且金属切除率高。又因加工切削速度是由刀具旋转速度和工件的回转速度合成形成，故加工时工件不需高速回转也能实现高速切削，从而有利于在工件转速相对较低状态下对大型工件进行高速切削，非常适合于各种大型薄壁回转件和细长轴类零件的加工[1],是一种高效外圆表面加工方法。我国目前机床的切削效率只有工业发达国家的一半,其中一个主要原因就是机械加工振动问题的限制[2]。

立铣刀高速车铣加工，在零件的加工精度、切削效率方面都能满足生产实际要求的一种先进的加工方法[3-4]。立铣刀高速车铣加工跟常规车铣加工一样具有变切深、变厚度的切削特性，由于立铣刀的多刃断续切削，加工零件表面常常留下振纹从而影响被加工零件的表面质量。开展立铣刀车铣切削的颤振稳定性研究具有重要的理论意义和实际应用价值[5-8]。切削颤振稳定性研究目前大多数研究学者集中在车削或两自由度的铣削，而对立铣刀四轴车铣加工颤振稳定性三自由度研究较少。如ALTINTAS等[9-10]对球头铣刀进行三自由度颤振稳定性研究，提出在频域内通过解析求解的方法获得球头铣刀加工颤振稳定域叶瓣图，从而有效提高球头铣刀的加工效率和加工精度。SHAMOTO等[11]建立了考虑球头刃倾角的铣削加工三维切削力模型进行球头铣削颤振的稳定性研究。SCHUBERT等[12]的高速车铣加工试验研究，结果表明采用耐磨刀具可实现难加工材料的切削加工，且在非振动区域可获得良好的表面质量。POGACNIK等[13]四轴车铣切削动态稳定性的研究表明，加工振动对零件表面质量影响很大，且加工过程中的不稳定性可通过切削参数的优化来避免。

国内丛春晓等[14]建立了车铣细长轴的两自由度理论模型对加工颤振进行稳定性研究。李忠群等[15]分析了不同切削条件下铣削颤振稳定性，建立了理论建模并对其优化。汤爱君等[16]综述了铣削过程中颤振的三维稳定性理论及三维稳定性图的研究状况，指出为了有效提高材料的去除率，必须研究机床转速、切削深度对加工颤振稳定性的影响。石莉等[17]在四轴车铣加工薄壁件试验中，通过调整合成切削速度来避开颤振敏感区。以上研究都为立铣刀四轴车铣加工三维颤振稳定性的研究奠定了一定的基础。YANG等[18]用振动刀具来抑制颤振，使切削振幅大幅降低。冯冬菊等[19]在脆性材料的加工中，采用超声波振动的方法抑制加工颤振，而本文研究的是立铣刀采用较大切深提高材料去除率加工回转体零件四轴车铣三维颤振稳定性，在高效切除材料的同时仍要获得良好的表面质量。立铣刀四轴车铣加工过程中由于进给方向(X)、法向(Y)和铣刀轴向(Z)切削力的相互作用，因此对立铣刀四轴高速车铣加工X，Y，Z三个方向的颤振稳定性进行研究是非常有意义的。

1 立铣刀车铣三维颤振的分析建模

如图1所示，四轴车铣加工时铣刀的回转轴线与工件的回转轴线相互垂直，其加工过程包括工件和铣刀两个旋转运动及铣刀的直线进给运动。由于四轴车铣的加工对象大多是大型回转体和细长轴这类零件，所以铣刀的直线进给运动一般采取轴向进给运动。

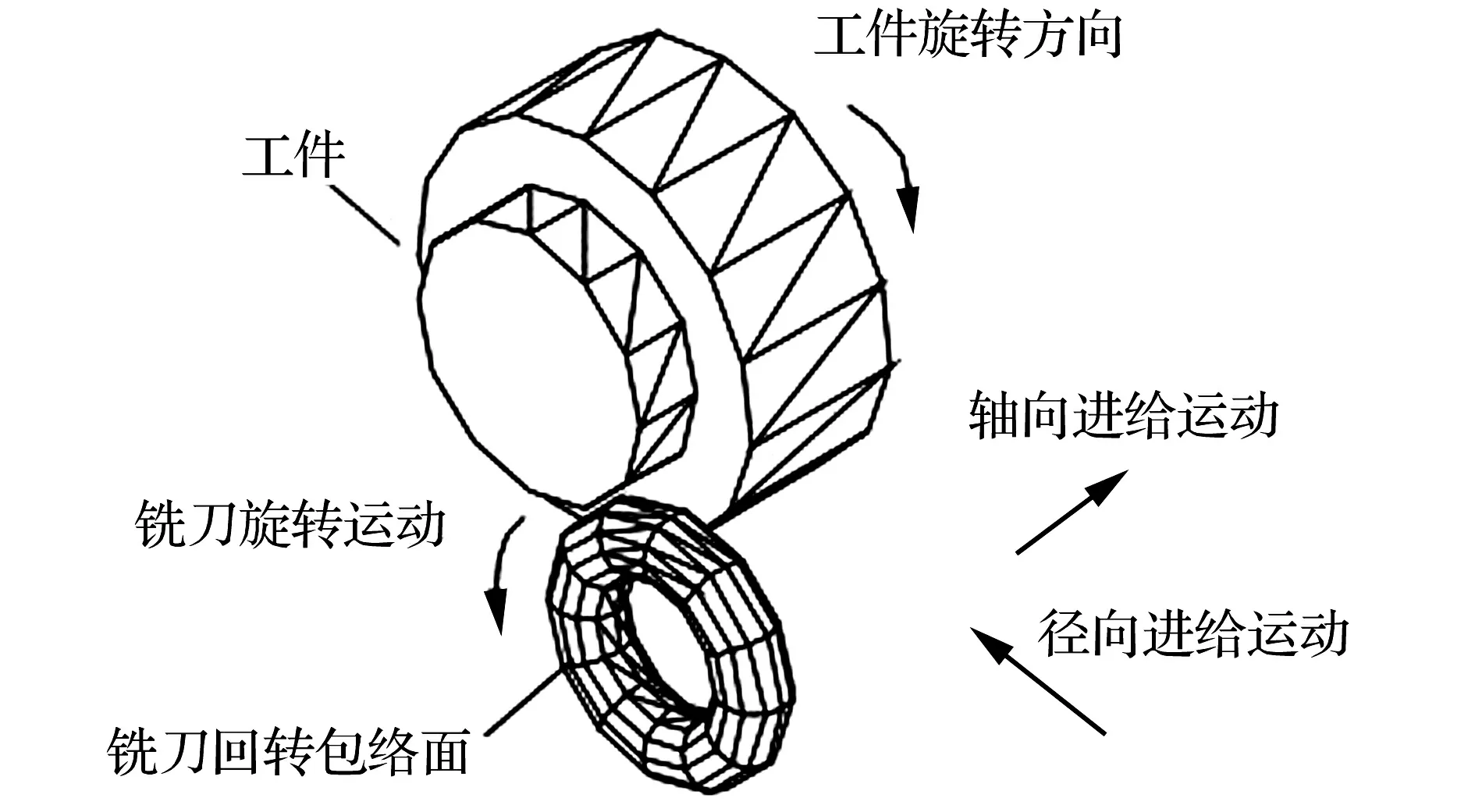
图1 四轴车铣加工的主要运动Fig.1 Mainly movements in 4-axial turn-milling

立铣刀四轴正交车铣加工时切削力在进给方向(X)、法向(Y)和铣刀轴向(Z)的切削力分析如图2所示。先对直齿立铣刀进行分析再延伸到螺旋铣刀，假定立铣刀有N个刀齿，切削力在X、Y和Z三个方向，引起的动态位移分别为x,y,z。当前刀齿j的动态位移表示为

vj=(xsinφj+ycosφj)cosα-zsinα

(1)

式中:α为侧刃切削厚度δp(Φj)方向与底刃切削厚度δf(Φj)方向的夹角;Φj为刀齿j的瞬时接触角，法向(Y) 轴顺时针测量。

(2)

式中:R为工件半径;r为立铣刀半径;αp为切削深度 ;fz为每齿进给量;e为切削点与旋转中心的距离;γ为旋转坐标与原坐标的夹角;Δθz为工件相对于铣刀两个相邻刀齿之间的转角。

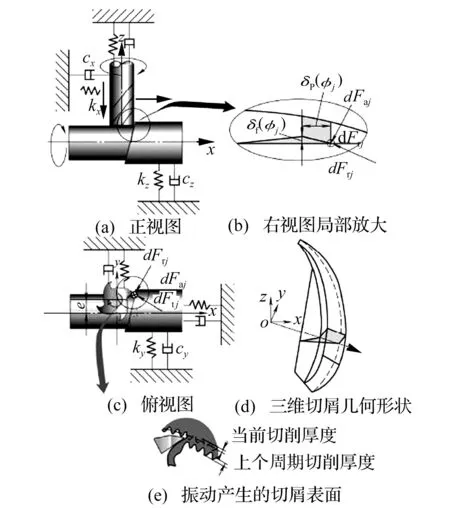
图2 车铣切削力模型及振动时切屑形状Fig.2 The model of turn-milling and shape of chip when dither is produced

图2中:kx，ky，kz分别为工艺系统在X,Y,Z方向上的刚度系数；cx，cy，cz分别为工艺系统在X,Y,Z方向上的阻尼系数；dFtj，dFrj，dFaj分别为切削刃j在切向、法向、轴向上的受力单元。

若立铣刀以角速度ω旋转，其接触角随着时间变化为φj=ωt。加工时产生的切削厚度可视为由两部分构成:一部分是立铣刀作刚体运动时产生的固定切削厚度δs(Φj);另一部分是前一刀齿与当前刀齿因振动引起的可变切削厚度变化部分。所以产生的总切削厚度可以表示为

δ(φj)=[δs(φj)+(vj,q-vj)]g(φj)

(3)

式中:vj,q为前一刀齿的动态位移;g(Φj)f为单位阶跃函数，用来确定刀齿是否处于切削中。

g(φj)=1Φpst<Φj<Φpex

g(φj)=0Φpst<Φj或Φj>Φpex

其中，Φpst，Φpex为切入角与切出角。

因固定切削厚度不影响产生再生振动的可变切削厚度，所以固定切削厚度部分在表达式中不再出现，其可变切削厚度为

δd(φj)=

(Δxsinφj+Δycosφjcosα-Δzsinα)g(φj)

(4)

Δx为X方向上的动态位移，是当前刀齿j与前一刀齿周期所产生的。

Δx=x(t)-x(t-T)

t为刀齿切削时间;T为两刀齿之间的周期;Δy为Y方向上的动态位移，是当前刀齿j与前一刀齿周期所产生的。

Δy=y(t)-y(t-T)

Δz为Z方向上的动态位移，是当前刀齿j与前一刀齿周期所产生的。

Δz=z(t)-z(t-T)

由式(4)可知，作用在刀齿j上的轴向切削力Faj，切向切削力Ftj和径向切削力Frj与可变切削厚度δd及轴向切削深度ap成正比。

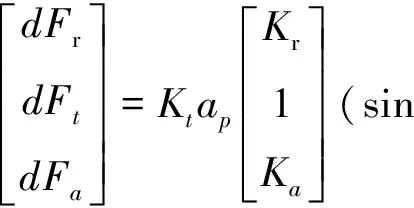
式中，Ka，Kr，Kt分别为轴向、径向、切向的切削力系数。

将切削力在X，Y，Z三个方向进行分解得

(6)

叠加作用在立铣刀各刀齿上所有切削力，可得刀具上的总切削力为

(7)

由刀齿切削力表达式和切削厚度表达式可得相应矩阵形式为

(8)

式中，矩阵A为随时间变化而变化定向动态切削力系数矩阵。

将刀齿切削力在时域中用矩阵形式来表示，式(8)可表示为

(9)

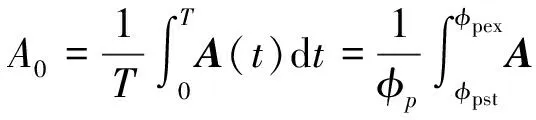
(10))

式中:A0为定向切削系数矩阵，该矩阵取决于接触角大小且不随时间变化;Фp为立铣刀的齿间角。

无论是直齿立铣刀还是螺旋立铣刀每一刀齿在一个切削周期内的平均切削力一致，所以前述A0对于螺旋立铣刀同样适用。如图3所示，加工过程的物理分析揭示了立铣刀四轴车铣加工中切削力函数的高次谐波在实际加工切削过程中被低通滤波。在加工中若有颤振存在，其再生振动谱的主颤振频率为ωc。

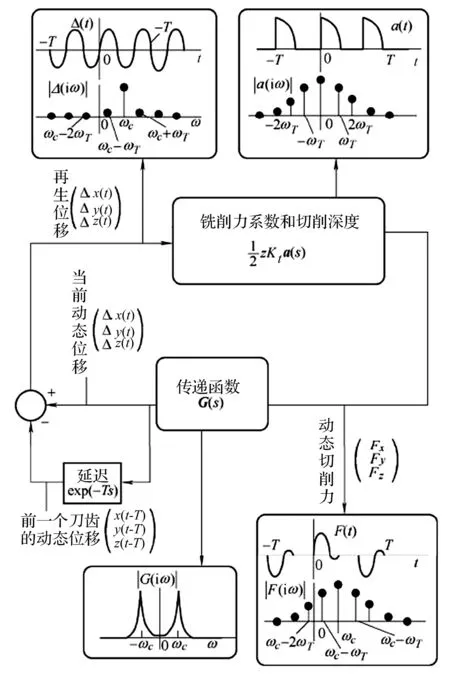
图3 立铣刀铣削时的再生颤振Fig.3 The regenerative dither by end mill during machining

图3中，G(s)为传递函数，a(s)为定向切削系数积分函数，ωT为谐波处的刀齿切削频率，Δ(t)为合成再生位移，Fx，Fy，Fz分别为在X,Y,Z方向上的动态切削力，F(t)为合成动态切削力。

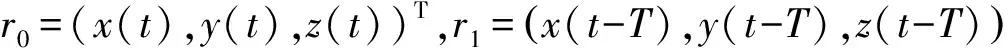
Δ(t)=r0(iωc)-r1(iωc)=

[1-exp(-iωcT)]exp(iωct)G(iωc)F(t)

(11)

式中，G(iω)为立铣刀—工件接触区的传递函数矩阵

(12)

此时切削力可以表示为

G(iωc)F(iωc)exp(iωct)

(13)

该特征方程的特征值为

(14)

将特征值和exp(-iωcT)=cosωcT-isinωcT代入，可得在颤振频率ωc处的临界切削深度

(15)

式中:ΛR为特征值的实部;k为切削圆弧时留下的振纹的整数。

ωcT=π-2φ+2kπ=ε+2kπ

刀齿切削周期T为

(16)

由式(16)可得立铣刀转速

2 立铣刀车铣加工颤振稳定性实验研究与结果分析

立铣刀四轴车铣加工三维颤振稳定域的研究是先由激振试验获取模态参数，接着根据得到的模态参数进行频率响应函数和颤振稳定域叶瓣图仿真，最后对理论模型和仿真结果进行实验验证。

实验设备如下：在欧马科技MV610四联动加工中心，进行激振和颤振稳定性试验。试验用刀柄：KENNAMETAL DV30ER25060；刀具：成都英格(Chengdu EAGLE)ZE12.21.4-30立铣刀，4条切削刃，直径为12 mm。选用直径为60 mm的硬铝(2A12)作为实验工件,工件用三爪夹卡盘夹紧，悬长为200mm。数据采集卡型号Kistler公司的5697A；切削力传感器为Kistler公司的9225B；位移传感器采用PHILTEC Model RC20；加速度传感器为3225F1(Sensitivity: 10.00 mV/g)；做加工颤振稳定性实验时考虑切削要素中切宽、进给速度对颤振的产生影响小于切深和切速，本次切宽取刀具直径的80%(9.6 mm)，F取400 mm/min，如图4所示。

图4 立铣刀四轴车铣加工颤振稳定性试验Fig.4 Trial of dither stability in 4-axial turn-milling by end mill

由于传递函数的对称性和模态矩阵的特性，可知表1中立铣刀三个方向的模态参数Gxy=Gyx，Gyz=Gzy，Gzx=Gxz。原点传递函数Gxx，Gyy和Gzz，通过用冲击锤在加速度计安装位置冲击该结构测得。而交叉传递函数是对加速度计安装位置的另一位置进行冲击测得，如Gxy，Gyz和Gzx。将所得数据用(n×n)阶多项式进行曲线拟合，通过拟合的曲线可估算出各模态的阻尼、固有频率及刚度的数值。

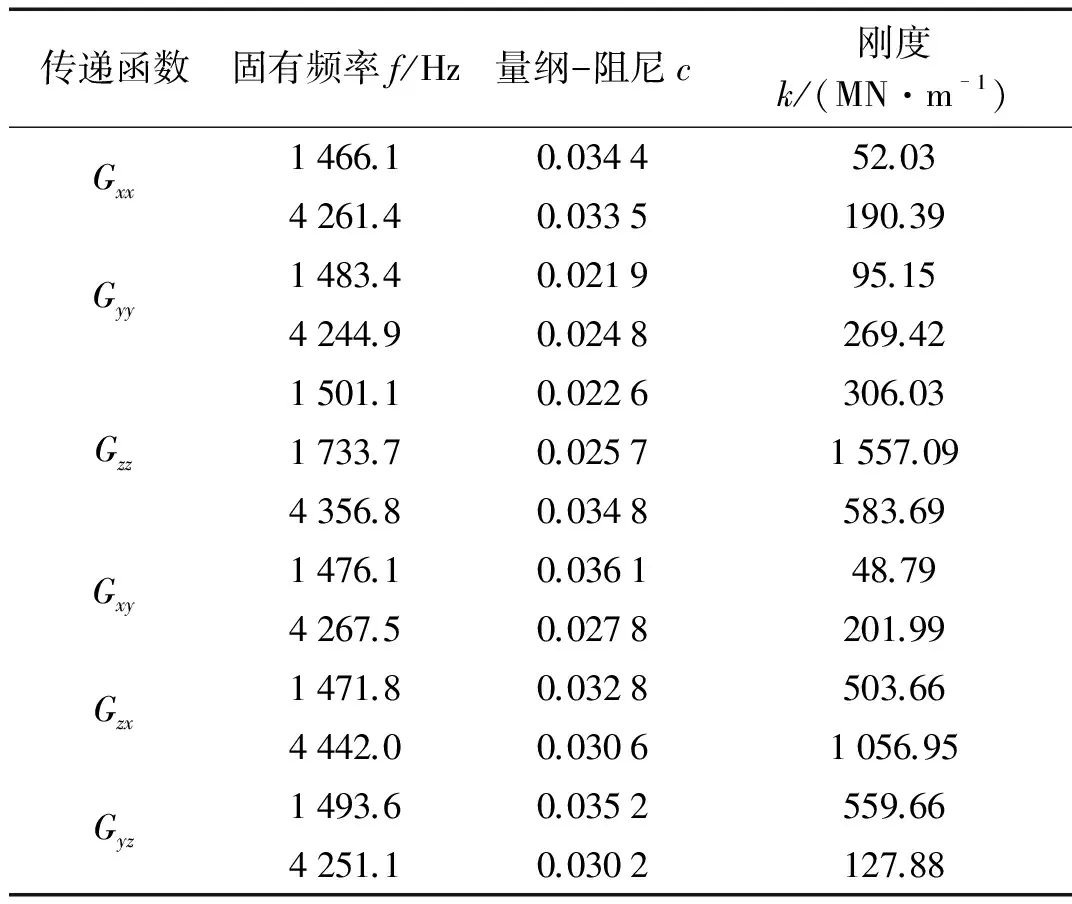
表1 立铣刀三个方向的模态参数

图5～图7为立铣刀刀尖在X,Y,Z三个方向上的仿真曲线与实验曲线对比图，是以原点传递函数，模态参数作为初始条件获得的理想曲线，其结果不仅可用来预测实际刀尖点响应函数，同时也为颤振仿真分析提供条件，扫描整个传递函数的主模态使其实部为负值的频率部分。

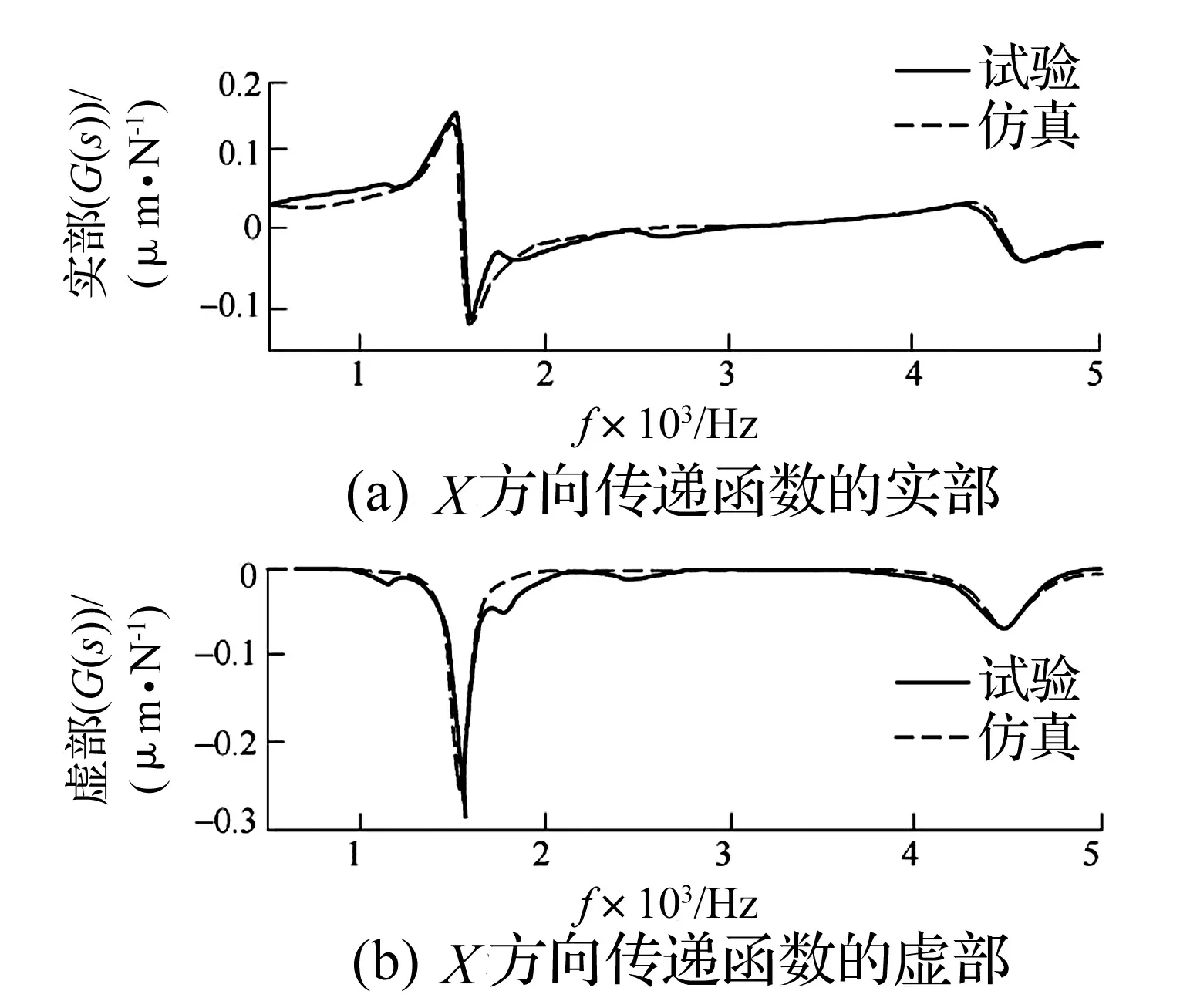
图5 X方向的传递函数Fig.5 Transfer function in X direction

在进行车铣加工颤振稳定性试验前，需先测量切削力系数；因切削力系数大小与铣刀磨损程度有关。铣刀磨损程度对叶瓣图的形状产生较大的影响，当铣刀磨损较小时，预测的稳定域内叶瓣图是比较准确；随着铣刀磨损的加剧，需根据铣刀的磨损程度重新测量切削力系数，以实现准确预测立铣刀四轴车铣加工颤振的稳定域。

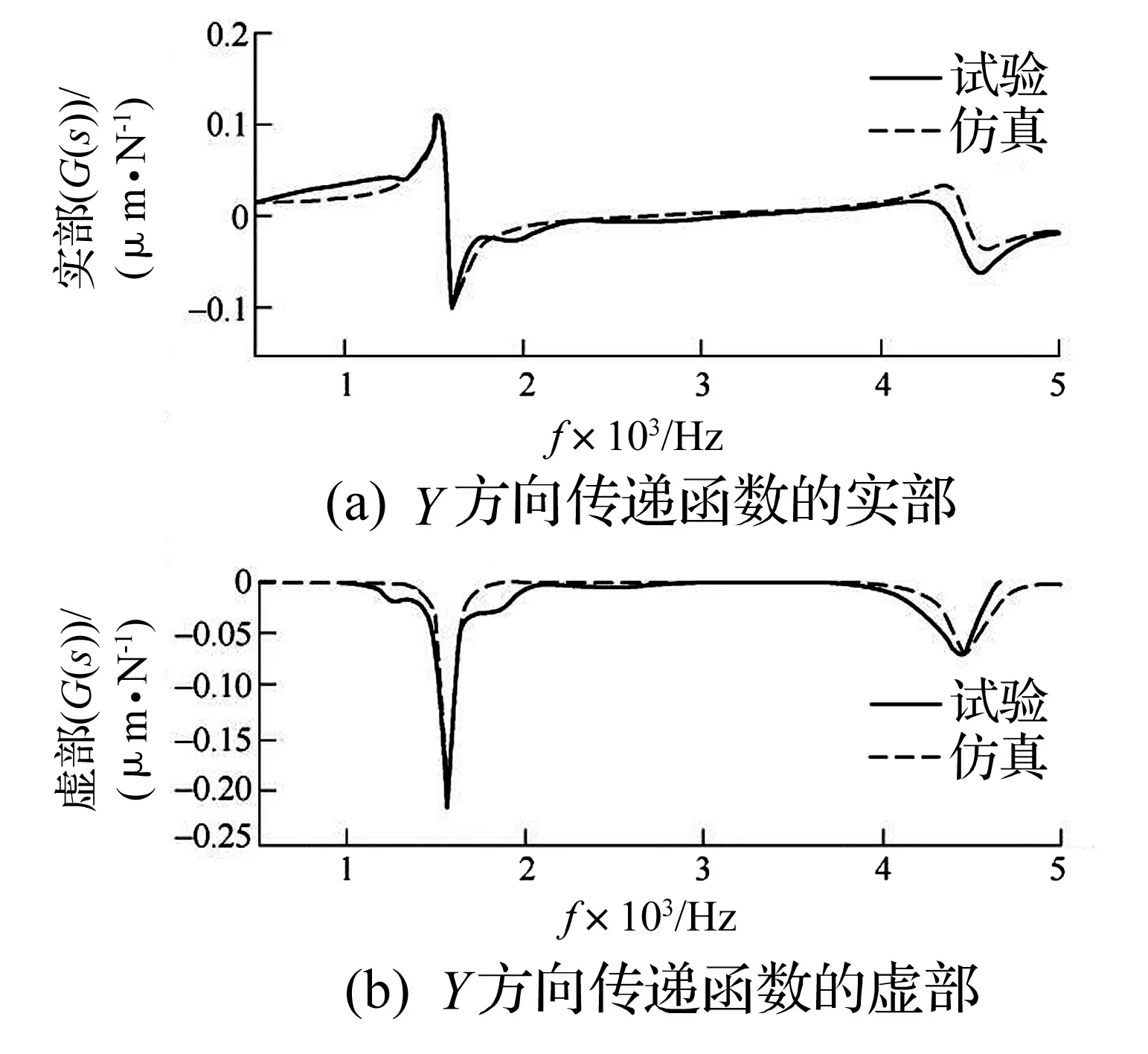
图6 Y方向的传递函数Fig.6 Transfer function in Y direction

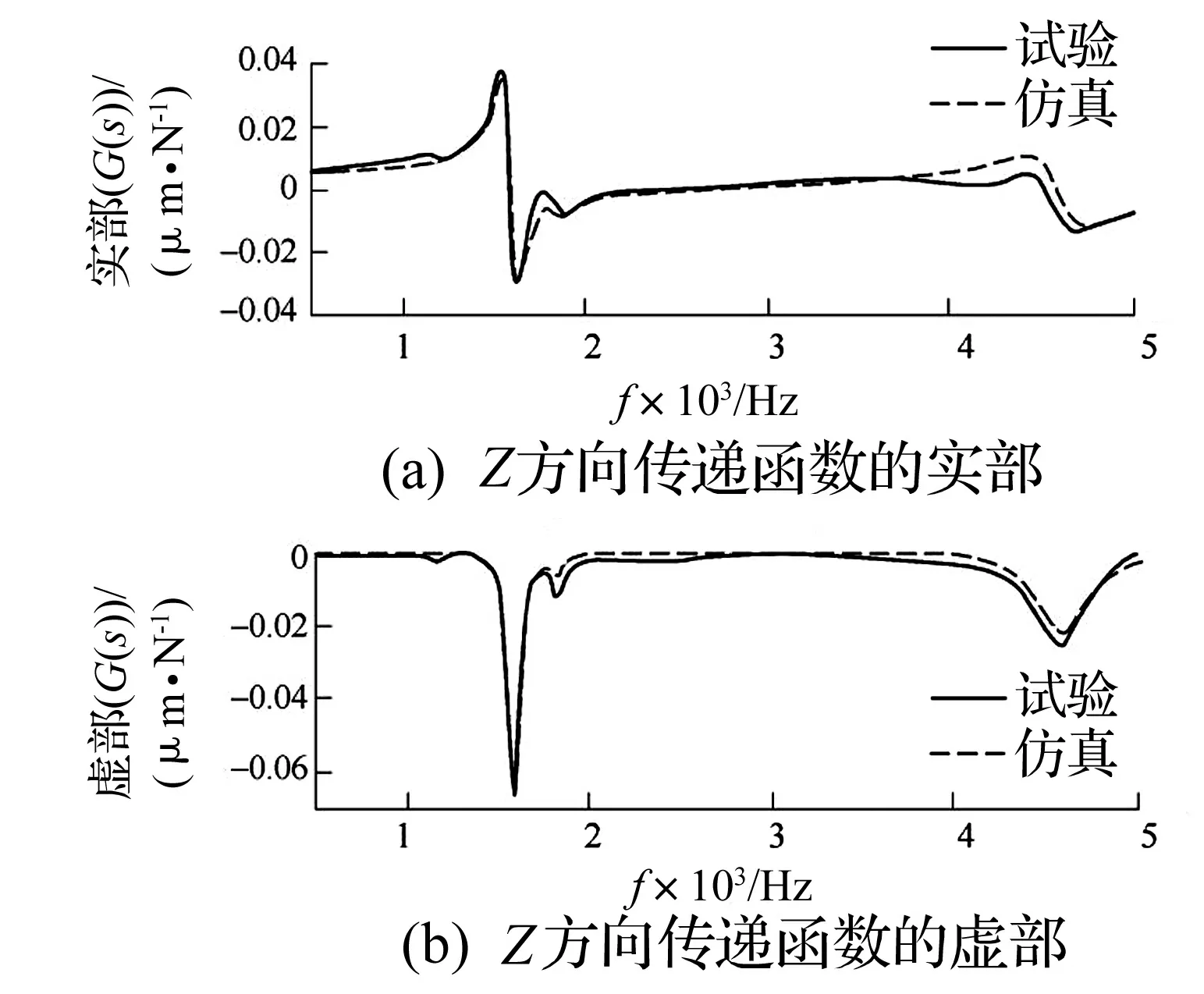
图7 Z方向主轴的传递函数Fig.7 Transfer function of principal axis in Z direction

图8为立铣刀四轴车铣加工的稳定性叶瓣图和力频谱分析。图8(a)为立铣刀侧刃加工时的三维颤振稳定性叶瓣图，从图8(a)上可以看出发生颤振部位是在叶瓣内，而叶瓣外面及以下部分在整个加工过程中没发生颤振。图8(b)、(e)、(g)分别为位置1处的加工零件的表面质量，切削力和颤振的频谱分析；图8(d)、(f)、(h)分别为位置3处的加工零件表面质量，切削力和颤振的频谱分析；图8(a)中图示三个位置立铣刀的切深均为2 mm，位置1处立铣刀转速为2 400 r/min，产生严重的颤振现象，从图8(g)力频谱得到验证，此时颤振发生在工艺系统第一模态的1 608 Hz位置附近；图8(a)中位置2处立铣刀转速为2 700 r/min，可见轻微颤振的产生；图8(a)中位置3处立铣刀转速为3 600 r/min，未产生颤振，同时力频谱显示强迫振动为240 Hz左右及其整数倍，此频率为主轴频率或刀齿的切削频率；因此加工时可通过选择不同的转速和切削深度，来有效避免颤振的产生，并预测加工的稳定性；但在稳定域叶瓣图上仍出显现一些微小的颤振，故仍需对该三维颤振稳定域模型作进一步的优化。

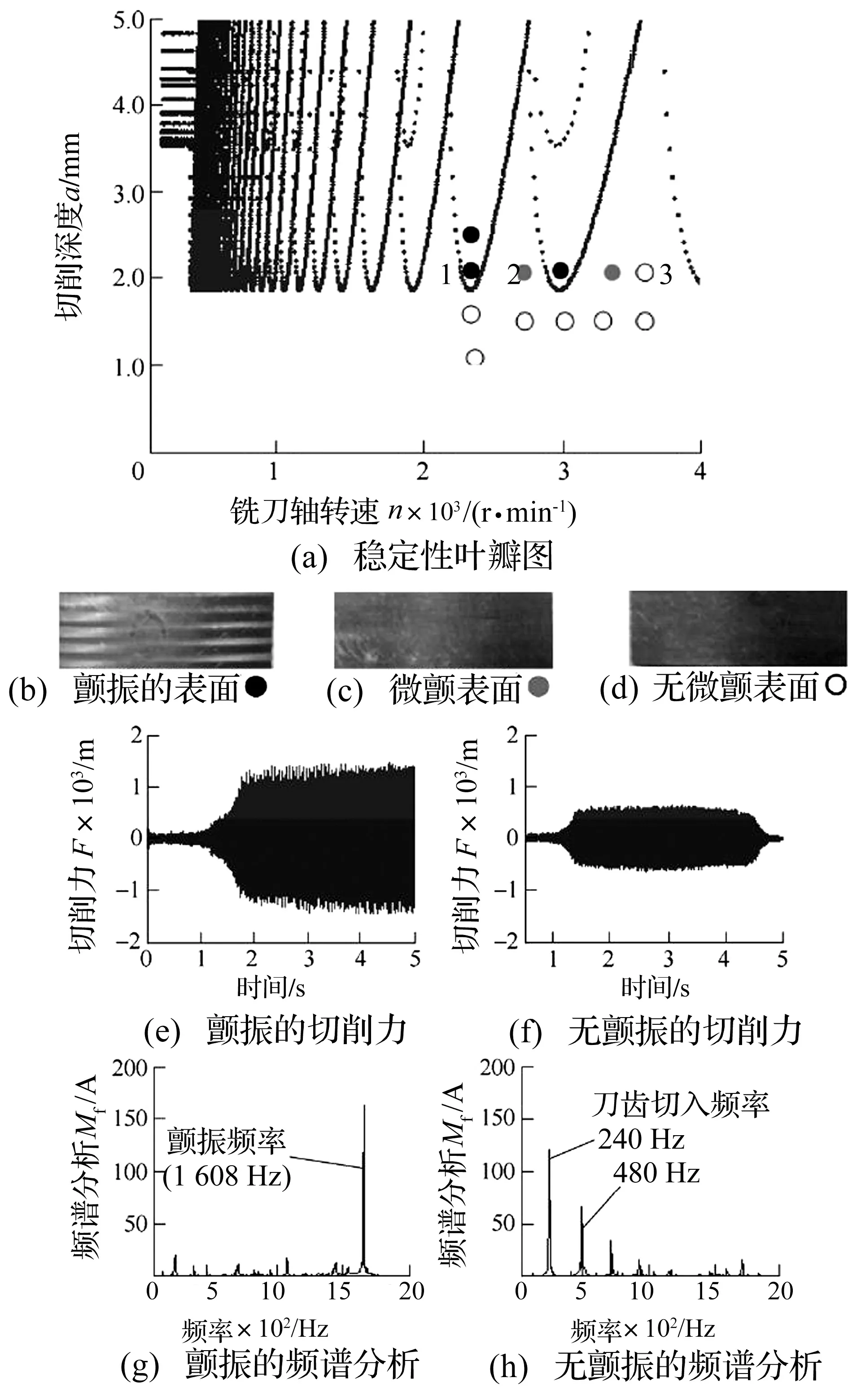
图8 四轴车铣加工的稳定性叶瓣图及频谱分析Fig.8 The stability range leaf figure of dither and analysis of spectrum in 4-axial turn-milling

3 结论

(1)立铣刀高速车铣加工产生颤振的条件与除了与立铣刀几何形状和啮合条件、机床结构的三个方向上频响应函数、工件材料特性等有关外，主要与铣刀的转速和切削深度密切相关；其切削加工产生颤振频率发生在工艺系统的主模态频率附近；发生颤振时的切削力是无颤振状态的几倍，甚至十几倍且表面粗糙度值急剧上升。

(2)通过对立铣刀四轴车铣加工零件的表面粗糙度测量和切削力频谱的分析，表明该理论模型和仿真结果的正确性，因此加工中可通过切削深度、主轴速度参数的合理选择来避免颤振的产生，为同类零件的加工效率和表面质量提供相应的理论指导。

[ 1 ] 勾治践，于骏一. 变速切削的研究现状[J]. 吉林工学院学报，1997，18(4)：14-17. GOU Zhijian, YU Junyi. The present status of the suppression of chatter in metal cutting with varying spindle speed[J]. Journal of Jilin Institute of Technology, 1997, 18(4): 14-17.

[ 2 ] 贾春德，姜增辉. 正交车铣运动的矢量模型及表面粗糙度的理论分析[J]. 机械工程学报，2001，37(3)：62-64. JIA Chunde, JIANG Zenghui. Vector modeling of orthogonal turn-milling movement and theoretical analysis on roughness of surface [J]. Chinese Journal of Mechanical Engineering, 2001, 37(3)：62-64.

[ 3 ] KORIC, STEPHAN, UDILJAK T, et al. Study of thesuitability of the machining of rotating surfaces[J]. Transactions of Famena, 2008, 32(2): 69-83.

[ 4 ] CHOUDHURY S K, BAJPAI J B. Investigation inorthogonal turn-milling towards better surface finish[J]. Journal of Materials Processing Technology, 2005, 170(3): 487-493.

[ 5 ] GUAN Yueqi, GUAN Hanqing, WANG Gaosheng. The modeling of cutting force in high-speed milling for end mill[J]. Sensors & Transducer, 2014(8): 210-217.

[ 6 ] SABAHUDIN E, EDIN B, AMIRA S. Comparison of machined surface quality obtained by high-speed machining and conventional turning[J]. Machining Science and Technology, 2006, 11(4): 531-551.

[ 7 ] 姜增辉，贾春德. 无偏心正交车铣理论切削力[J]. 机械工程学报，2006，42(9)：23-28. JIANG Zenghui, JIA Chunde. Theoretical cutting force of non-eccentricity orthogonal turn-milling[J]. Chinese Journal of Mechanical Engineering, 2006, 42(9)：23-28.

[ 8 ] 朱立达.车铣加工中心动态特性及其加工机理的仿真与试验研究[D]. 沈阳：东北大学，2010.

[ 9 ] ALTINTAS Y. Analytical prediction of three dimensional chatter stability in milling[J]. JSME International Journal, 2001, 44(3): 717-723.

[10] ALTINTAS Y, STEPAN G, MERDOL D. Chatter stability of milling in frequency and discrete time domain [J]. Annals of the CIR, 2008, 1(1): 35-44.

[11] SHAMOTO E, AKAZAWA K. Analytical prediction of chatter stability in ball end milling with tool inclination[J]. CIRP Annals-Manufacturing Technology, 2009, 58(1): 351-354.

[12] SCHUBERT A, NESTLER A, FUNKE R.Precision Engineering and Nanotechnology[C]//Italy:11th International.Conference of the European Society,2011: 480-483.

[13] POGACINK M, KOPAC J. Dynamic stabilization of theturn-milling process by parameter optimization[J]. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, 2000, 214(4): 127-135.

[14] 丛春晓，刘恒，吕凯波，等. 细长轴切削颤振的稳定性分析和实验研究[J].振动与冲击，2012，31(5)：73-76. CONG Chunxiao, LIU Heng, LÜ Kaibo, et al. Stability analysis and test for cutting chatter of a slender shaft[J]. Journal of Vibration and Shock, 2012, 31(5): 73-76.

[15] 李忠群，刘强. 圆角铣削颤振稳定域建模与仿真研究[J].机械工程学报，2010，46(7)：181-186. LI Zhongqun, LIU Qiang. Modeling and simulation of chatter stability for circular milling[J]. Journal of Mechanical Engineering, 2010, 46(7)：181-186.

[16] 汤爱君，刘战强. 铣削加工系统三维稳定性理论研究与进展[J]. 工具技术，2008，42(5)：3-5. TANG Aijun, LIU Zhanqiang. Perspectives and progress in three-dimensional stability lobes in milling chatter system[J]. Tool Engineering, 2008, 42(5): 3-5.

[17] 石莉，陈尔涛，姜增辉.正交车铣铝合金薄壁回转体振动信号的试验分析[J].兵工学报，2009，30(3)：356-360. SHI Li, CHEN Ertao, JIANG Zenghui. Test analysis on vibration signal of thin aluminium-alloy cylinder machined with orthogonal turn-milling[J]. Acta Armamentarii, 2009, 30(3): 356-360.

[18] YANG F, ZHANG B,YU J. Chatter suppression via an oscillating cutter[J]. Journal of Manufacturing Science and Engineering, 1999, 121(1): 54-60.

[19] 冯冬菊，赵福令，徐占国，等. 超声波铣削加工材料去除率的理论模型[J]. 中国机械工程，2006，17(13)：1399-1403. FENG Dongju, ZHAO Fuling, XU Zhanguo, et al. Mathematic model of material removal rate for ultrasonic milling[J]. China Mechanical Engineering, 2006, 17(13): 1399-1403.

Stability analysis and experimental research for three-dimensional dither in processing of high speed milling

GUANYueqi1,WEIKexiang1,2,ZHANGWenming3,GUANHanqing4

(1. Department of Mechanical Engineering, Hunan Institute of Engineering,Xiangtan 411101, China; 2.Hunan Province Cooperative Innovation Center for Wind power Equipment and Energy Conversion, Xiangtan 411101, China; 3. State Key Laboratory of Mechanical System and Vibration,Shanghai Jiao Tong University, Shanghai 200240, China; 4.College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China)

Aiming at high speed turn-milling by end mill, the theoretical model in stability range of three-dimensional dither was established on the basis of its cutting principle by using an analytic method. Based on modal test of 4-axial turn-milling by end mill, the leaf figure of the dither stability range was simulated and analyzed. The results show that: the geometrical shape of mill, material of work-piece, rotating speed of mill, cutting depth and the frequency response function of machine-tool’s structure are closely related to the conditions that can produce dither in high speed turn-milling by end mill. In the test of stability range of dither in turn-milling, the results of spectrum analysis for cutting force show that: cutting is stable and non-dither when cutting-in frequency of cutter tooth plays the leading role in force spectrum. Dither is produced when modal frequency of the system plays the leading role in force spectrum. The measured value of cutting force and surface roughness are also higher than those in the condition of non-dither. Thus the theoretical model and results of simulation can provide theoretical guidance for processing efficiency and surface quality of work-piece manufactured by end mills.

end mill; high speed turn-milling; dither stability; modeling

湖南省科技计划(2013GK3028)

2016-03-25 修改稿收到日期：2016-06-29

关跃奇男，硕士，副教授，1964年4月生

TH161

10.13465/j.cnki.jvs.2017.04.030