基于三角函数的脉冲型近场地震动的近似模型
2017-03-09蒲武川梁瑞军戴枫禹
蒲武川, 梁瑞军, 戴枫禹, 黄 斌
(武汉理工大学 土木工程与建筑学院土木工程系,武汉 430070)
基于三角函数的脉冲型近场地震动的近似模型
蒲武川, 梁瑞军, 戴枫禹, 黄 斌
(武汉理工大学 土木工程与建筑学院土木工程系,武汉 430070)
对用于模拟脉冲型地震动的Makris模型的适用性进行了评价,通过对脉冲周期的计算方法的比较分析,发现从该模型推导的由实测最大位移和最大速度计算得到的周期过小估计了近场地震动的脉冲周期。考虑地震动正负速度幅值的不同,提出了一种新的基于三角函数的脉冲型近场地震动的近似模型,该模型用于具有单循环的脉冲型地震动,可模拟位移完全不复位、完全复位和部分复位的地震动。通过比较实测地震动和近似模型的时程曲线和反应谱,证明新模型具有较好的适用性。
近场地震;脉冲型地震动;近似模型;脉冲周期
近场地震动是指在断层附近记录到的地震动,在地震工程学上主要关注或更狭义的指具有脉冲特征的地震动。这些近场地震动中含有中长周期的速度脉冲,且具有较大的速度幅值,包含了较大的地震能量。1966年的Parkfield地震和1971年的San Fernando地震中记录到的波形使人们认识到了脉冲型地震动的存在[1],而BERTERO等[2]从工程学的角度首先发现具有脉冲特征的地震动会导致中长周期结构产生较严重的损伤。在之后的如1994 Northridge地震、1995日本神户地震、1999土耳其Izmit地震、1999台湾集集地震中,均发现脉冲型地震动的存在,其对结构的巨大的破坏作用也得到印证。
近场脉冲型地震动近年得到了大量研究,从脉冲的成因到其对各类结构的影响,以及针对此类地震动的结构设计方法等。近场地震动的脉冲特征通常由前向性效应(Forward Directivity)或永久位移效应(Permanent Displacement Effect or Fling Effect)引起。由于脉冲型地震动速度的窄带频谱特征,研究人员试图采用特定解析式来模拟脉冲型地震动的时程曲线。在满足精度要求的前提下,如果脉冲型地震动可以用特定的函数代替,那么基于近似模型求解结构响应的解析解成为可能,这将为结构地震响应分析和设计提供极大的便利。同时,在对脉冲型地震动的特征参数(脉冲周期、速度幅值等)与地震震级、断层类别等的关系进一步研究的基础上,可以对断层附近将来可能发生的脉冲型地震动的波形进行预测并应用到结构设计中。
研究人员提出的近似模型一般基于速度脉冲建立,有采用正弦或余弦波形、三角形波形[3-4]、小波等形式。基于正余弦函数的近似模型是其中主要的一种,其中由包括半个正弦波[5]、单个正弦波、带包络函数的正弦波[6-8]、带幅值调整系数的正弦波[9]等近似模型。根据地震动的时程曲线特征,可以分别采用不同的方法进行模拟。一般来说,近似模型的精度越高,需要的参数就更多,其拟合方法也越复杂。
另一方面,研究发现近场地震动的脉冲循环个数的增多会引起结构损伤的显著增加。通常采用速度时程的半循环的个数来衡量脉冲数量,而影响脉冲数量的机理较为复杂,通常认为与断层破坏面的形状等因素有关。BRAY等[10]统计了54条地震动的半循环数量,假定大于PGV(Peak Ground Velocity)的50%的半循环均作为一个脉冲,则脉冲个数为1和2个的地震波数量约占65%。即,地震动中大部分为半循环或单循环的脉冲。当然,定义脉冲门槛值(如前述的50%的PGV)越低,脉冲个数越多。
本文首先对基于三角函数的单循环脉冲地震动的近似模型(Makris模型)的适用性进行评价,对脉冲周期的计算方法进行比较分析,在此基础上提出一种单循环脉冲地震动的三角函数近似模型。本文提出的模型考虑了速度时程正负方向幅值的不同,可通过简单的表达式和较少的参数模拟单循环脉冲型地震动的速度、位移时程,并得到与实测地震动较为接近的反应谱。
1 基于三角函数的Makris模型的评价
HALL等根据速度波形研究了两类主要的脉冲型地震动,其中一类单方向的速度时程(Forward Motion Only),地表位移达到幅值后不复原,产生不可恢复的永久位移(等于最大位移),此类脉冲型地震动被称为A类地震动。另一类是具有正负两个方向速度的波动时程(Forward and Back Motion),如果速度时程在两个方向上波形一致(如一个正弦波),则地表位移达到幅值后完全复原,不产生永久位移,这类脉冲型地震动被称为B类地震动。HALL等采用了三角形的速度时程,加速度时程为矩形,如图1所示。
Makris利用上述A类、B类脉冲型地震动的定义,采用三角函数对两类近场地震动进行了模拟。其中A类地震动的加速度a、速度v和位移d的时程分别表示为
(1)
(2)
(3)
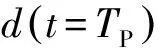
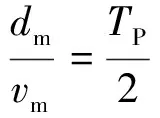
(4)
式中,dm、vm分别为位移和速度的绝对值的最大值。
采用与A类地震动的近似模型类似的方法,Makris提出了B类地震动的加速度、速度和位移时程分别表示为
a(t)=VPωPcos(ωPt), 0≤t≤TP
(5)
v(t)=VPsin(ωPt), 0≤t≤TP
(6)
(7)
与前述A类模型的方法类似,B类模型脉冲周期可由式(8)求得
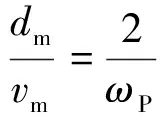
(8)
Makris模型采用了脉冲型地震动两个最主要的参数即速度幅值和脉冲周期,用较少的参数和简洁的表达式建立了近似模型。同时脉冲周期的计算方法从模型的函数表达式推导得到,方法严谨。但是,实际的地震动具有较强的随机性,有的地震动具有正负两个方向的速度时程,但是幅值不同,因此该类波形会形成小于位移幅值的永久位移。对此类地震动,前述模型均不适用。其次,按照前述脉冲周期的计算方法,周期还可以利用速度幅值和加速度幅值或位移幅值和加速度幅值来计算。对A类地震动可由式(9)和式(10)所示,其中am为加速度的绝对值的最大值。
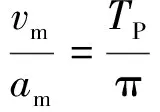
(9)
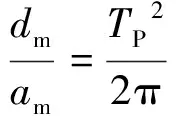
(10)
对B类地震动,可由式(11)和式(12)所示。
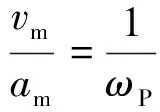
(11)
(12)
不采用加速度幅值的原因可能是高频分量的影响较大,采用加速度幅值计算得到的脉冲周期精度不够。尽管采用位移幅值和速度幅值计算脉冲周期更为适合,如下节所述,式(4)和式(8)仍较小的估计了地震动的脉冲周期。较小地估计脉冲周期,还会导致加速度被过大估计的问题。图2和图3分别表示了采用前述Makris模型对Lander地震Luceme波(采用A类模型)和Imperia地震ElCentro Array #4波(B类)的地震动时程曲线的拟合。可以看出,Luceme波存在位移部分恢复的特征,实际上介于A类和B类地震动之间;其次,式(4)和式(8)过小评价了实际的脉冲周期。
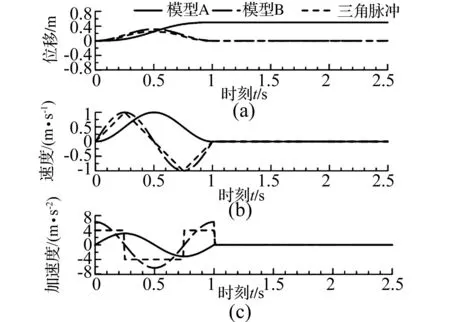
图1 三角函数模型和三角形(速度)模型Fig.1 Trigonometric model and triangle velocity model
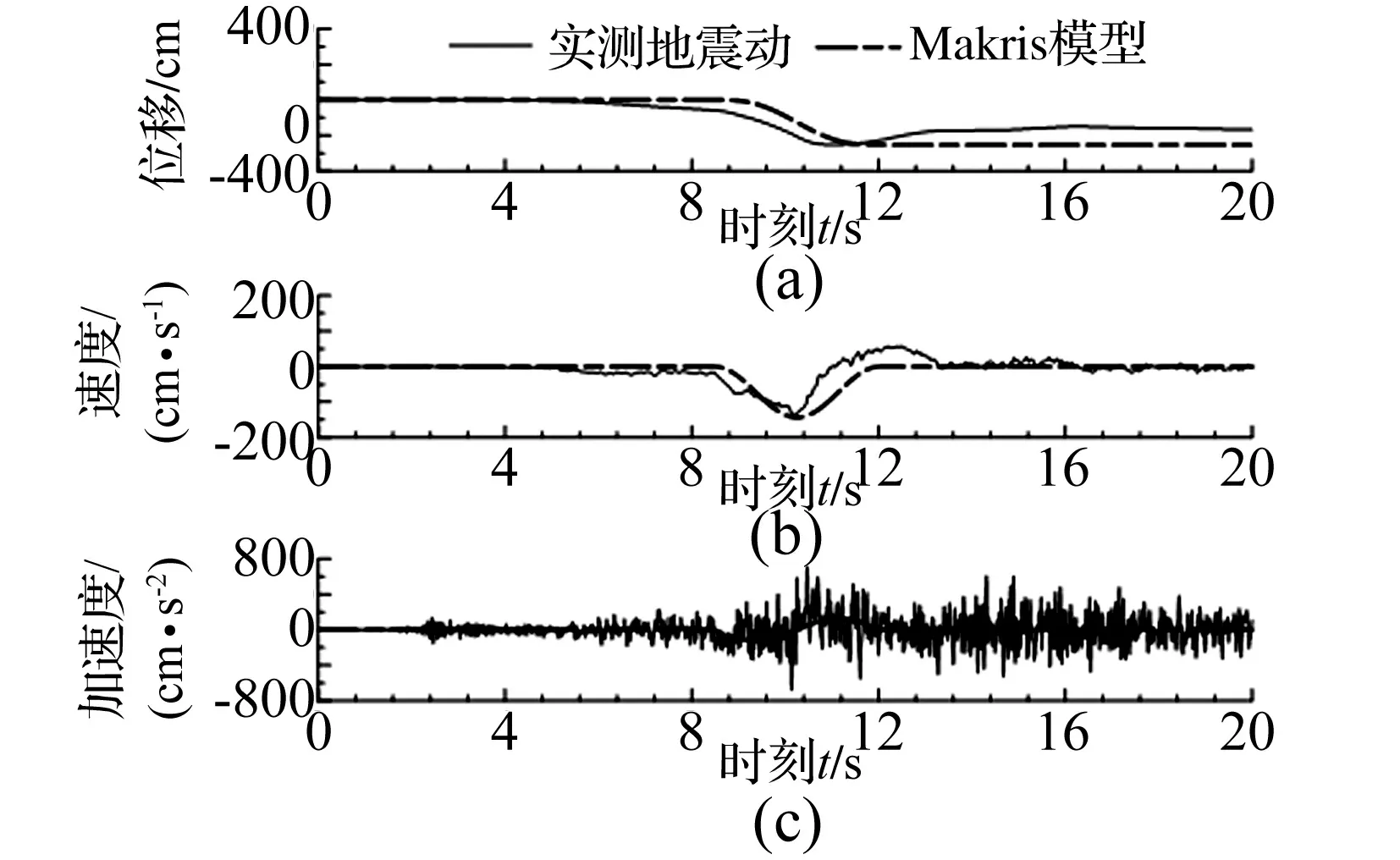
图2 Makris模型模拟Lander-luceme波(A类)Fig.2 Comparison of Makris model and type A record
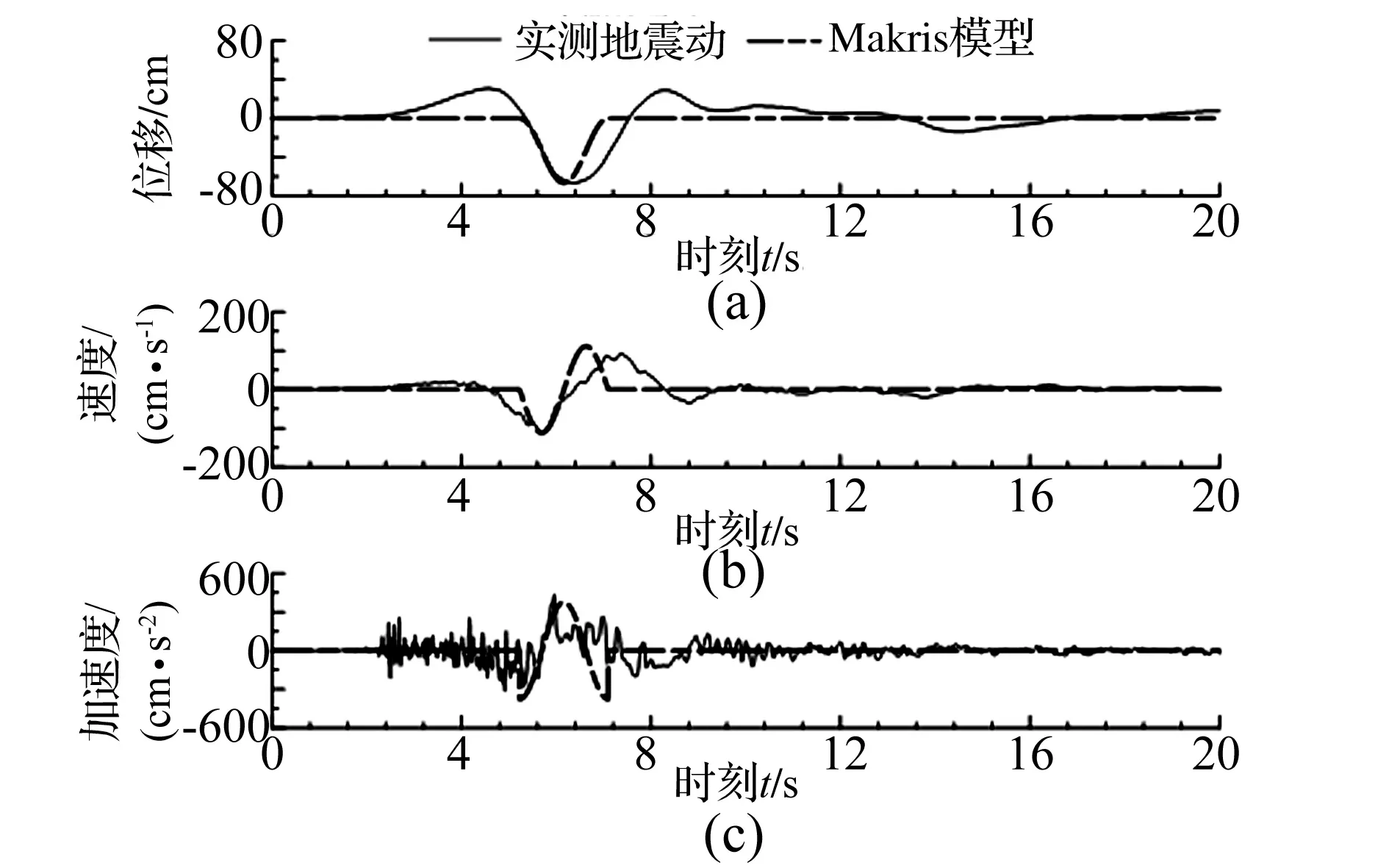
图3 Makris模型模拟Imperia-EICentro Array#4波(B类)Fig.3 Comparison of Makris model and type B record
2 脉冲型地震动脉冲周期比较
脉冲周期是脉冲型地震动的最为重要的特征参数之一。在建立地震动的近似模型时,选取合理的脉冲周期对模型的精度有重要的影响。基于前节所述Makris模型的问题,本节对各种计算脉冲周期TP的方法进行比较分析。
一种常用的方法是计算实测地震动的反应谱,取速度反应谱最大值对应的周期作为脉冲周期。由于反应谱随着阻尼比增大会变得越来越光滑,在脉冲周期附近呈现出来的波峰会越来越不明显。本文取阻尼比为5%时的反应谱的峰值对应的周期作为脉冲周期,用Tp,s表示。BAKER[11]介绍了一种采用小波从脉冲型地震动中提取脉冲的方法,其所提供的程序可以识别脉冲周期,本文采用其程序对地震动进行分析,得到地震动的脉冲周期Tp,B。同时采用BAKER的脉冲波判别指标PI进行判别,本文选取了16条脉冲型地震动,如表1所示。表1中列出了各地震波的Tp,s和Tp,B,以及位移、速度和加速度的峰值。
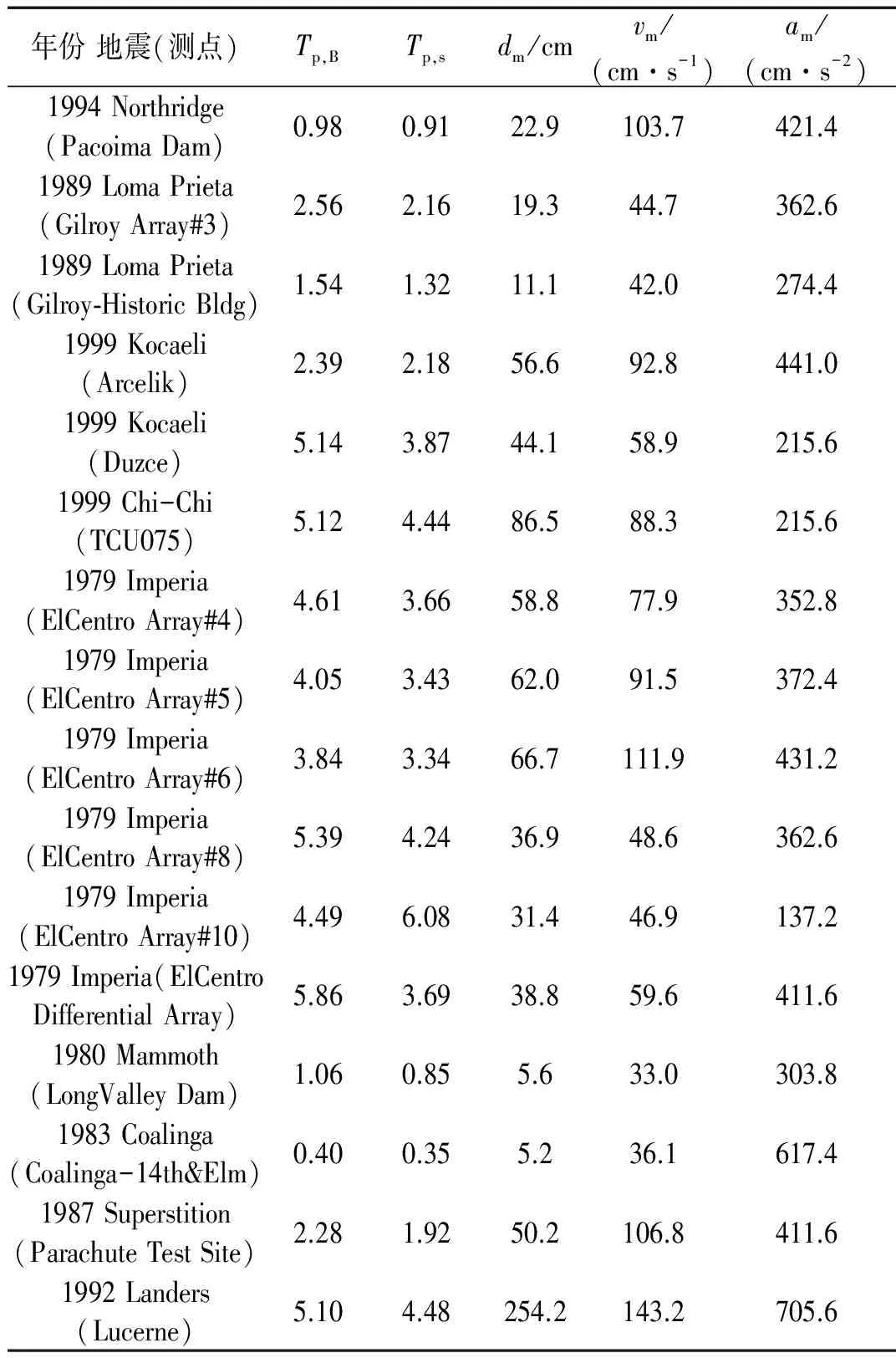
表1 选取的地震波列表
图4比较了Tp,s和Tp,B,发现除Imperia (El Centro Array #10)以外,Tp,B均略大于Tp,s。其原因是实测地震动反应谱仍包含高频成分的贡献,而Tp,B直接根据速度时程得到,因此Tp,B比Tp,s能更准确的描述地震动中的主要脉冲的周期。
本文以Tp,B为标准,对前述模型的脉冲周期计算方法进行评价。图5比较了Tp,B与由式(4)、式(8)、式(9)、式(10)、式(11)、式(12)计算得到的脉冲周期,可以看出基于Makris模型中位移、速度和加速度幅值计算得到的脉冲周期显著小于Tp,B,将其近似模型应用到结构分析中可能产生较大误差。
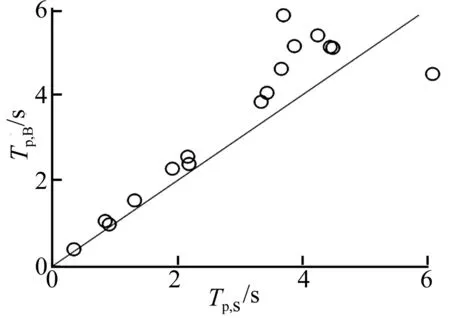
图4 脉冲周期比较Fig.4 Comparison of pulse period
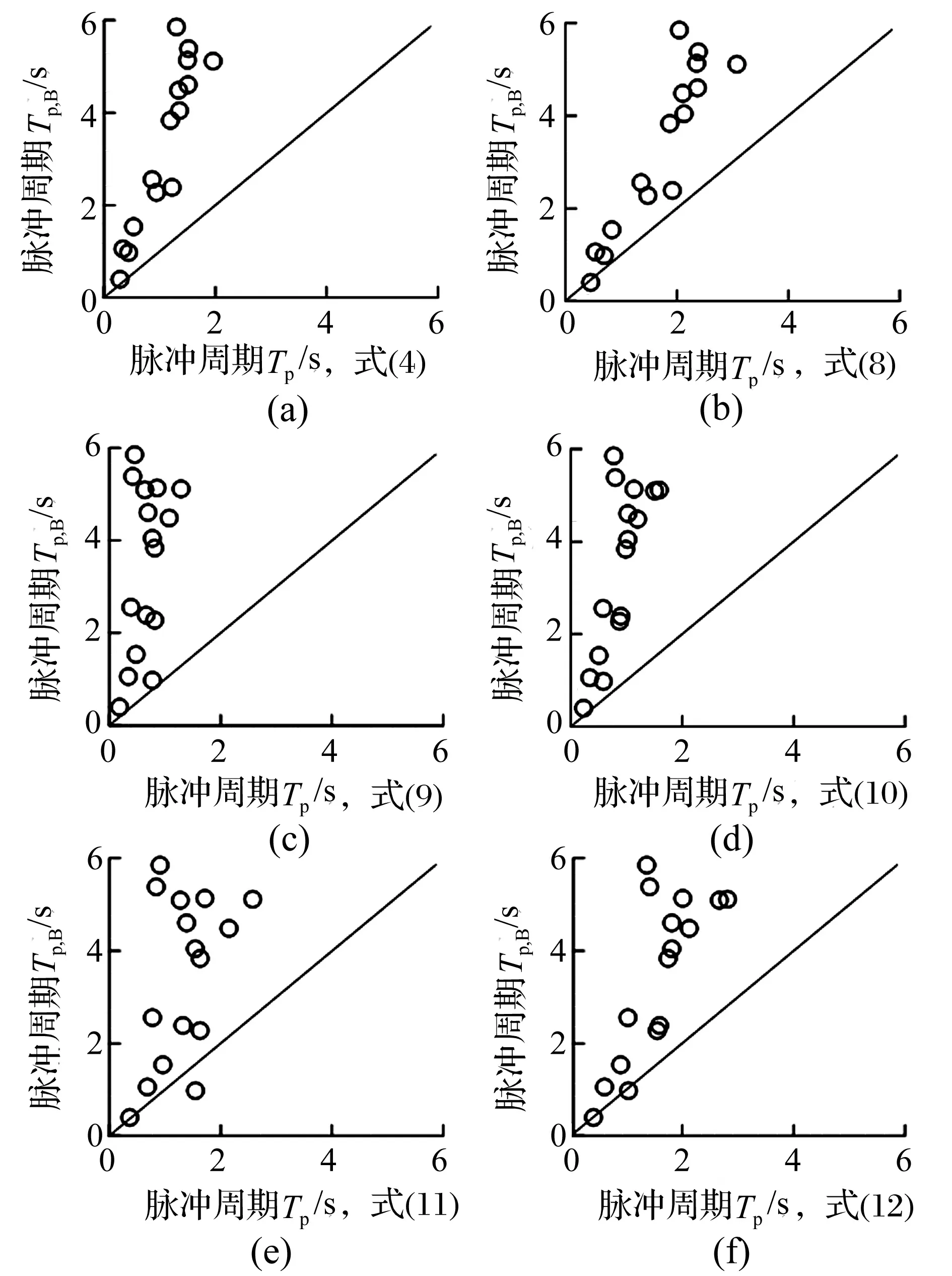
图5 脉冲周期比较Fig.5 Comparison of pulse period
3 考虑正负速度峰值差异的近似模型
在近断层地震动的实际记录中,存在许多介于A类和B类之间的地震动,即速度时程中正负向幅值相差较大,且正负向幅值较大不可忽略的情况。前述Makris模型不能考虑地震动的这种特征(见图2)。为了能更好的拟合此类地震动,本文提出新的模型,其位移、速度和加速度为
a(t)=VP1ωPcos(ωPt)+VP2ωPsin(2ωPt)
(13)
(14)
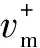
(16)
(17)
(18)
(19)
d(t)=
(20)
此时,若取0 (21) 式(21)所示比值与波形幅值和频率等参数无关。若取0 (22) 图7比较了Tp,B与基于最大位移与最大速度的式(22)得到的TP,可以看出,式(22)仍然较小地估计了地震动的脉冲周期。因此,此模型不采用由实测位移和速度峰值计算脉冲周期的方法,而采用Tp,B作为脉冲周期。 图6 本文模型的时程曲线图Fig.6 Time histories of the proposed model 图7 Tp,B与式(22)的脉冲周期的比较Fig.7 Comparison of Tp,B and period odtained from Eq.(22) 本文提出的模型适用于含有1个或2个脉冲的速度脉冲。由于其适用范围限定,因此相对于带包络函数的正弦波模型而言,参数量少且参数确定方法简单。同时,Makris提出的A、B类地震动均可通过该模型模拟。 图8 本文模型对EI Centro Array#5波的拟合Fig.8 Simulation of EI Centro Array#5 ground motion by the proposed model 图9 本文模型对Lucerne波的拟合Fig.9 Simulation of Lucerne ground motion by the proposed model 图10 EI Centro Array#5波与近似模型的反应谱比较Fig.10 Comparison of response spectra(EI Centro Array#5) 图11 Lucerne波与近似模型的反应谱比较Fig.11 Comparison of response spectra(Lucerne) 本文考虑采用三角函数对脉冲型近场地震动的波形进行近似,对既有的Makris模型进行了分析评价,发现采用速度、位移幅值计算的脉冲周期与实际脉冲周期差异较大,并建议采用Baker方法得到的脉冲周期。本文还对单循环脉冲型地震动提出考虑速度时程正负幅值差异的基于三角函数的近似模型,该模型基于地震动正负速度幅值和脉冲周期构建,参数少且形式简单,可以模拟位移无恢复、全恢复和部分恢复的脉冲型地震动。通过对实测地震动的时程曲线和反应谱的比较,认为该模型可以较好的模拟单循环脉冲型地震动。 [ 1 ] MAVROEIDIS G P, PAPAGEORGIOU A. A mathematical representation of near-fault ground motions [J]. Bulletin of Seismological Society of America, 2003, 93(3): 1099-1131. [ 2 ] BERTORO V V, MAHIN S A, HERRERA R A. Aseismic design implications of near-fault San Fernando earthquake records [J]. Earthquake Engineering and Structural Dynamics,1978, 6(1):31-42. [ 3 ] ALAVI B, KRAWINKLER H. Consideration of near-fault ground motion effects in seismic design [C]//Proceeding of 12th World Conference of Earthquake Engineering.Auckland: The NewZealand Society for Earthquake Engineering ,2000:2665 [ 4 ] HALL J F, HEATON T H, HALLING M W, et al. Near-source ground motions and its effects on flexible buildings [J]. Earthquake Spectra,1995, 11(4): 569-605. [ 5 ] MAKRIS N. Rigidity-plasticity-viscosity: can electrorheological dampers protect base-isolated structures from near-source ground motions? [J]. Earthquake Engineering and Structural Dynamics,1997,26(5): 571-591. [ 6 ] 田玉基,杨庆山,卢明奇. 近断层脉冲型地震动的模拟方法[J]. 地震学报,2007, 29(1): 77-84. TIAN Yuji, YANG Qingshan, LU Mingqi. Simulation method of near-fault pulse-type ground motion[J]. Acta Seismologica Siniea,2007, 29(l):77-84. [ 7 ] HE W L, AGRAWAL A K. Analytical model of ground motion pulses for the design and assessment of seismic protective systems [J]. Journal of Structural Engineering, 2008, 134(7): 1177-1188. [ 8 ] TAKEWAKI I, MOUSTAFA A, FUJITA K. Improving the earthquake resilience of buildings [M]. London: Springer-verlag, 2014: 43-64. [ 9 ] 李新乐,朱晞. 近断层地震动等效速度脉冲研究[J]. 地震学报, 2004, 26(6): 634-643. LI Xinle,ZHU Xi. Study on equivalent velocity pulse of near-fault ground motions[J]. Acta Seismologica Siniea,2004, 26(6): 634-643. [10] BRAY J D, RODRIGUEZ-MAREK A. Characterization of forward-directivity ground motions in the near-fault region[J]. Soil Dynamics and Earthquake Engineering,2004, 24(11): 815-828. [11] BAKER J W. Quantitative classification of near-fault ground motions using wavelet analysis [J]. Bulletin of the Seismological Society of America, 2007, 97(5): 1486-1501. An analytical model for approximating pulse-like near-fault ground motions PUWuchuan,LIANGRuijun,DAIFengyu,HUANGBin (Department of Civil Engineering and Architecture,Wuhan University of Technology, Wuhan 430070, China) Analytical models based on trigonometric functions are used to describe the pulse-like near-fault ground motions, and Makris model is one of the typical. In this paper, the Makris model was investigated first. It is found that the pulse period obtained analytically from the peak displacement and peak velocity underestimates the predominant period of the record. A new analytical approximation model was proposed to consider the difference of maximum and minimum velocity in the main cycle of velocity time history. The model could be applied to simulate those one-cycle pulse ground motions, including the motions with forward displacement, forward-backward displacement and forward-partially backward displacement. Examples were also presented to show that the new approximation model was useful to simulate the one-cycle pulse type ground motions. near-fault earthquake; pulse-like ground motion; approximation model; pulse period 国家自然科学基金(51208405) 2015-12-07 修改稿收到日期:2016-02-22 蒲武川 男,博士,副教授,1980年生 TU20 A 10.13465/j.cnki.jvs.2017.04.033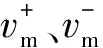

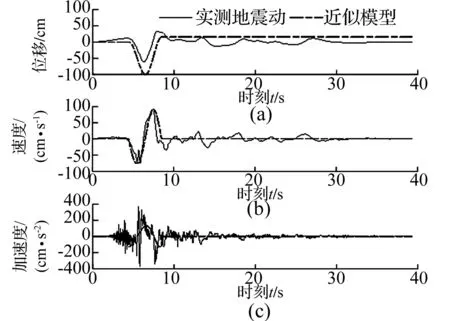
4 近似模型对实测地震动的拟合
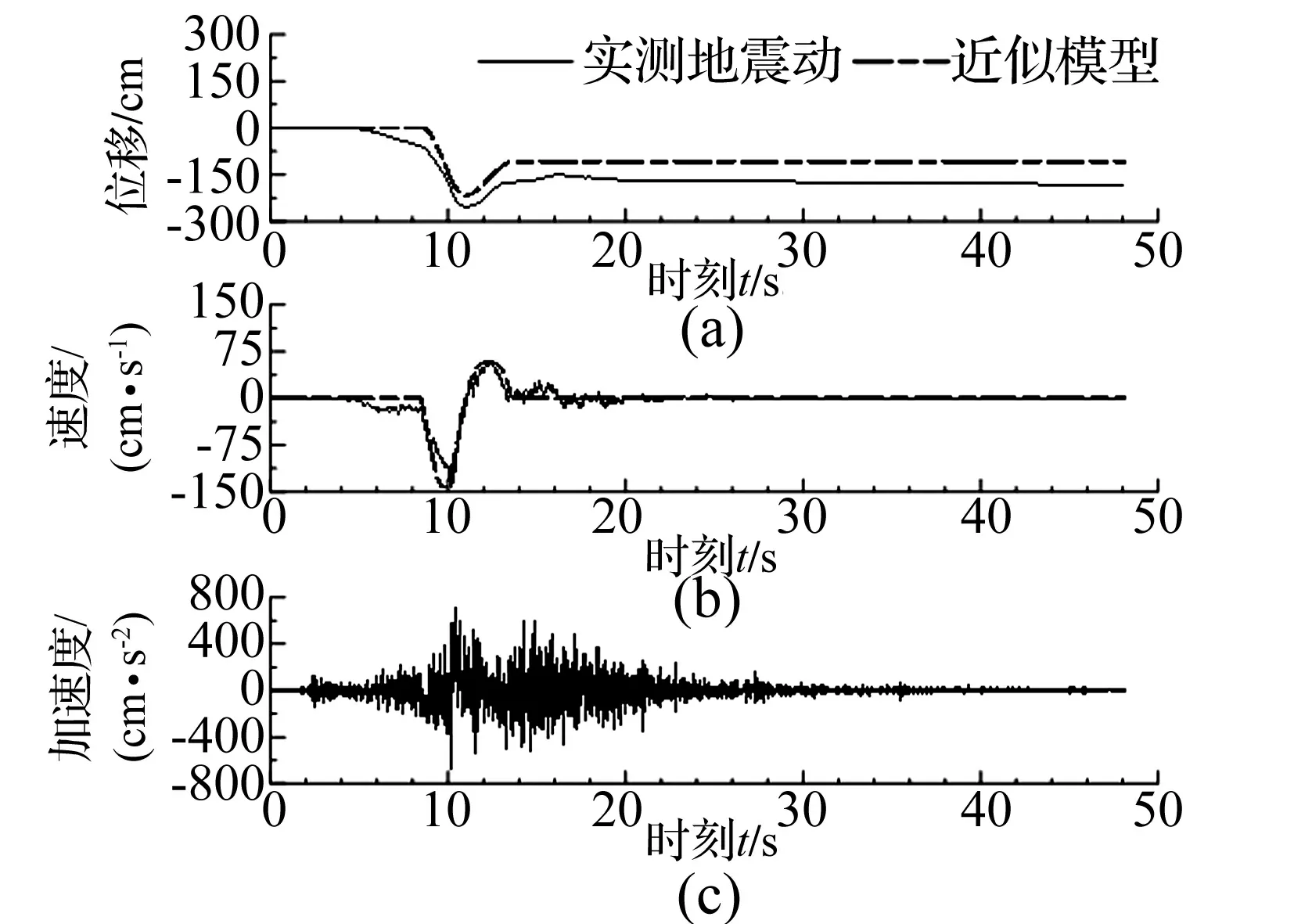
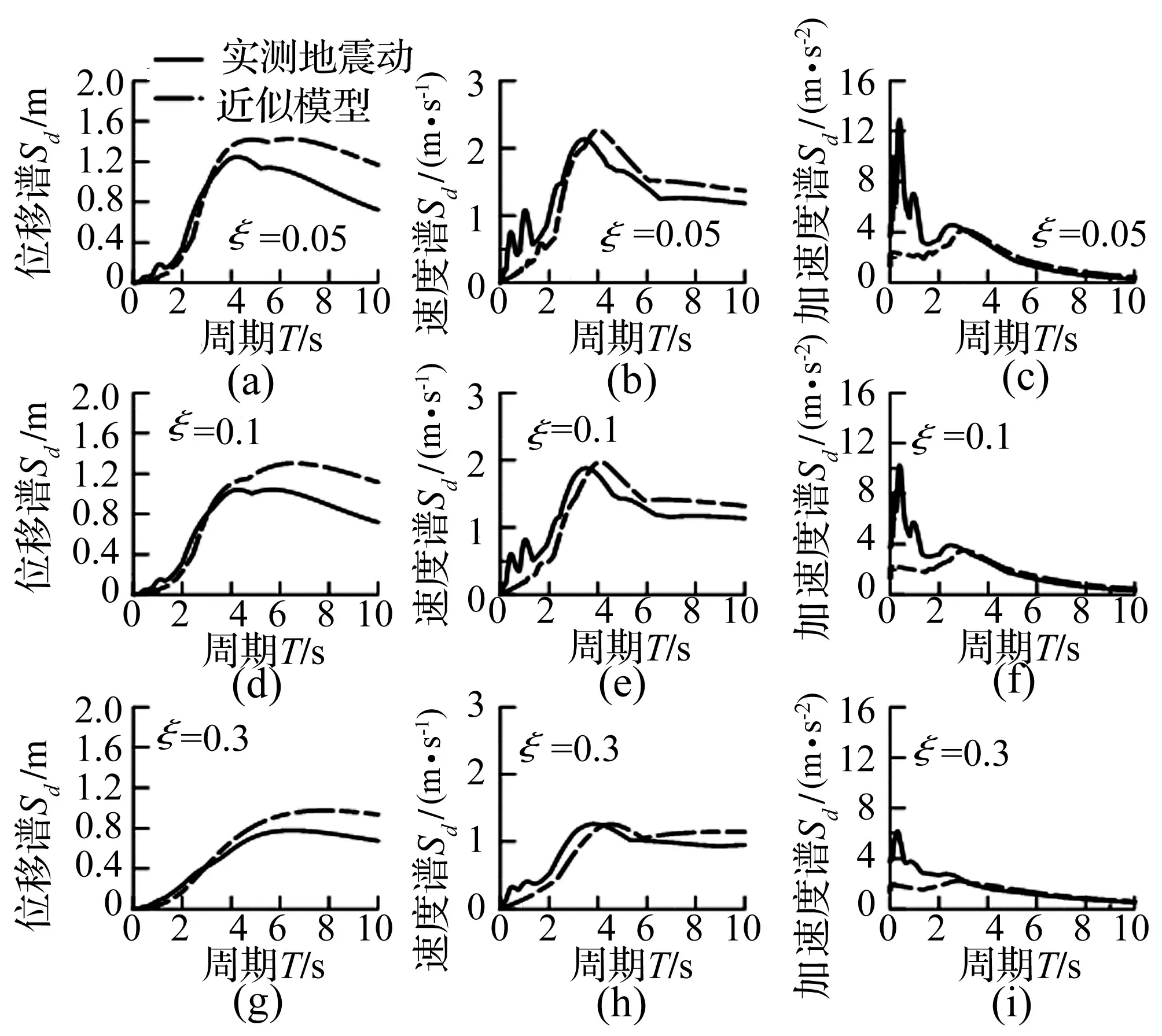
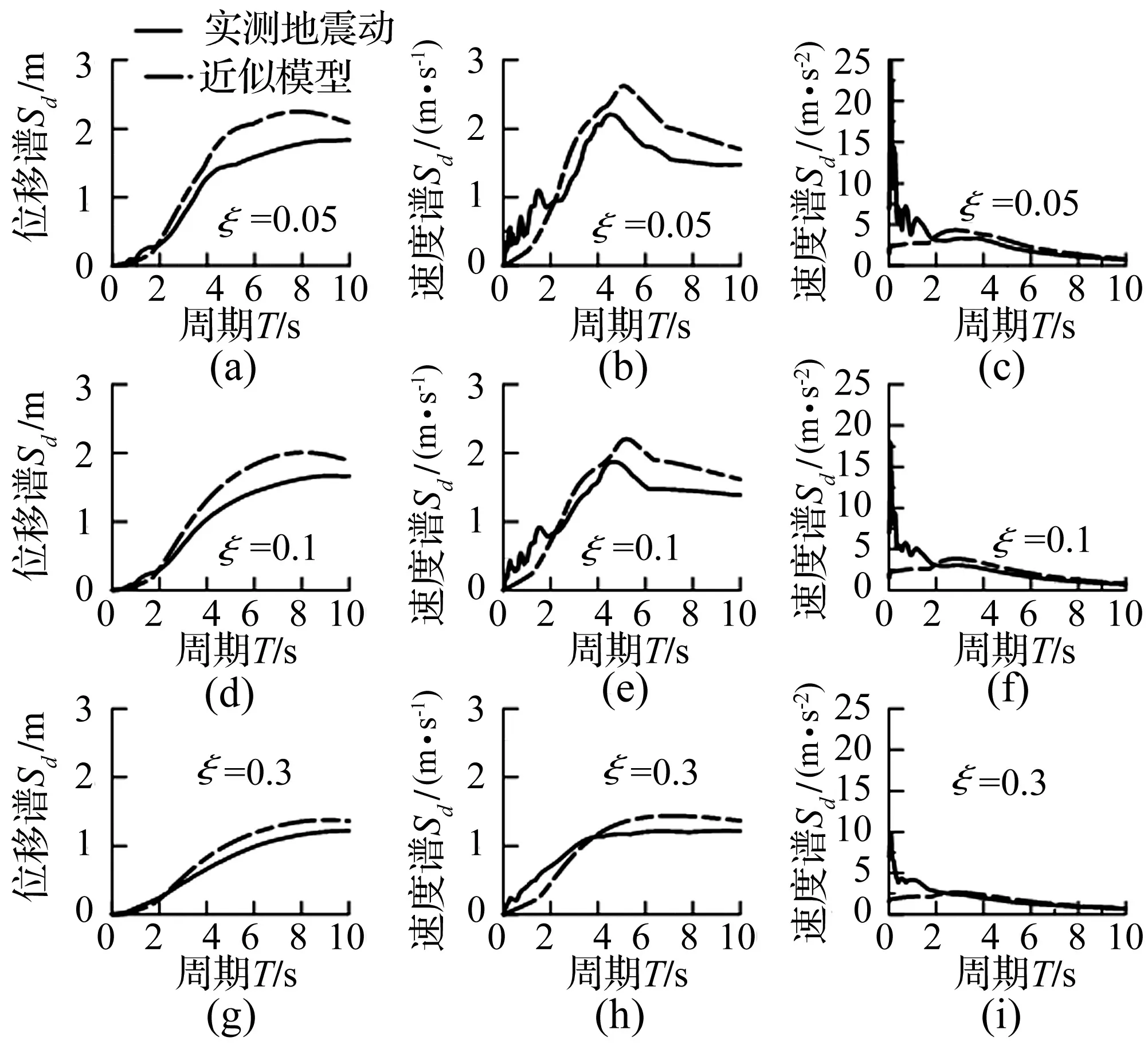
5 结 论
