基于ICA-CEEMD小波阈值的传感器信号去噪

赫 彬， 张雅婷， 白艳萍

(中北大学 理学院，太原 030051)

基于ICA-CEEMD小波阈值的传感器信号去噪

赫 彬， 张雅婷， 白艳萍

(中北大学 理学院，太原 030051)

针对传感器在采集信号时混入不同的噪声，提出一种基于ICA-CEEMD小波阈值的组合去噪算法。该方法是对一维含噪信号进行剪切分段、平移和拼接，得到几个不同的含噪信号作为独立分量分析(ICA)的输入通道信号。通过ICA的盲源分离技术使得信号和噪声进行初步分离。再利用互补集合经验模态分解(CEEMD)对分离信号进行分解去噪，由于不同的高频和低频噪声，需要对分解的高阶和低阶固有模态函数(IMF)进行处理。对第一层和最后一层IMF利用3σ原则提取细节信息，进一步抑制模态混叠影响，重构去噪信号。最后，利用小波阈值对重构信号做去噪处理，提升去噪效果和性能指标。为验证该方法的有效性，进行了仿真和中北大学汾机实测实验，结果表明，该方法在去噪效果和性能指标上都优于小波软阈值去噪和基于CEEMD的小波阈值去噪方法，是一种有效的信号去噪新方法。

ICA-CEEMD；小波阈值；传感器；去噪；3σ原则

著名的“鸡尾酒会问题”(Cocktail Party Problem)是指在嘈杂的环境中，人的注意力可以集中在某一个人的谈话之中而忽略掉背景中其他的对话或噪音的一种听力选择能力。鸡尾酒会现象有两种体现形式:①当人将注意力集中到某个特定声源上，就可以忽略掉其他声音；②当人的听觉器官突然受到某个外界刺激时，可以迅速分离其他干扰而获得该声源信息[1]。正如在传感器信号处理领域中，信号在传递和接收过程中会混入不同的噪声，快速有效地将信号和噪声分离有助于尽早地获得源信号信息。当信号中携带的信息是具有先验性时，可以通过信息的先验知识来对信号进行适当的数学变换以尽可能准确地提取信息。而盲源分离技术是在对信号源和系统传输通道特性未知且在无先验知识可利用的条件下，仅基于一些假设条件即可得到源信号或系统传输特性的一个估计或复制，进而可以将信号从噪声中分离而获得所需源信号信息[2-3]。

目前，关于提取传感器水声微弱信号的方法很多[4-5]，主要有傅里叶滤波法、小波变换法、快速独立分量分析法(Fast Independent Component Analysis，Fast ICA)、自适应滤波法和经验模态分解法(Empirical Mode Decomposition，EMD)等[6]，这些方法对含噪传感信号有一定的去噪效果，但是也存在一些缺点。其中由DONOHO等提出的小波变换法在信号处理中取得了很好的效果，但是小波变换法缺点在于小波基和分解层数的选择[7]。芬兰阿尔托大学理工学院HYVARINEN等提出的Fast ICA方法是基于非高斯性最大化原理，其分离得到的各分量不仅互不相关，而且还尽可能高阶统计独立，故能更好地反应数据的本质特征。但其不足之处在于分离的信号仍有大部分噪声，而且需要多维信号输入输出来选择去噪信号[8]。HUANG等[9-10]提出的一种新的时频分析方法—经验模态分解法，其不但可以根据信号的特征自适应选择基底来对信号进行多分辨率分析的特点，而且还克服了小波基的选择。但其也有不足之处，主要在于分解的固有模态函数(Intrinsic Mode Function，IMF)会产生模态混叠的情况，导致在重构去噪信号时，仍有大量噪声混入其中。为了降低模态混叠的影响，WU等[11]又在EMD基础上提出了集合经验模态(Ensemble Empirical Mode Decomposition，EEMD)，该方法利用加入辅助白噪声来降低了模态混叠影响。YEH等[12]又对EEMD做了改进，提出了互补集合经验分解法(Complementary Ensemble Empirical Mode Decomposition，CEEMD)，将加入的辅助噪声采用正、负成对的形式，这样就能消去重构信号中辅助噪声，降低模态混叠影响，并且可以减少加入的噪声集合次数，提高计算效率。

本文为了更好的将传感器信号与噪声分离，提出了一种基于ICA-CEEMD的小波阈值去噪方法，在仿真实验中，向信号加入不同的噪声，将该含噪信号剪切为四段，再按顺序分别平移四段信号，得到的三个新的信号与原含噪信号组成Fast ICA的输入通道信号，执行Fast ICA得到初步的去噪信号。然后将该去噪信号利用CEEMD分解为四层IMF，可以看出源信号的频谱基本集中在IMF2和IMF3上，而由于模态混叠影响，在IMF1和IMF4内仍有小部分源信号存在。再利用3σ原则提取IMF1和IMF4的细节信息，得到新的IMF1和IMF4并重构去噪信号。最后，对重构信号进一步利用小波软阈值去噪来提升信噪比和去噪效果。本文方法在去噪效果和性能指标上都明显优于小波软阈值去噪和基于CEEMD小波阈值去噪方法。将该方法应用到中北大学汾机测试实验的信噪分离中，结果显示，该方法具有良好的可行性和实用性。

1 基本原理

1.1 独立分量分析(ICA)

ICA是从多元数据中寻找其内在具有统计独立和非高斯的因子或成分的一种盲源分离方法，对n个未知信源S经混合矩阵A线性混合为信号X，即

X=AS

(1)

式中,混合信号(观测信号)X是由独立源信号S经不同A线性加权得到的。进行ICA处理的目的就是找到一个混合信号X的解混矩阵W，使得输出的信号尽可能独立，即

Y=WX=WAS=GS

(2)

式中，G为系统矩阵，通过迭代计算使得G=I(I为对应单位矩阵)。本文所用的是由芬兰阿尔托大学理工学院HYVARINEN教授提出的基于负熵最大的快速独立分量分析(Fast ICA)，又称固定点算法。该算法采用牛顿迭代算法对观测变量的大量采样点进行批处理，以最大化负熵作为目标函数，每次从观测信号中分离出一个独立成分量，经过多次分离，可以将所需信号分离出来。

1.2 互补集合经验模态分解(CEEMD)

CEEMD方法是在EEMD方法基础上实现的,加入的辅助噪声采用正、负成对的形式，这样就能够很好地消除重构信号中的残余辅助噪声，并且加入的噪声集合次数可以很低，计算效率较高。

CEEMD方法的具体过程:

(1)在原始信号中加入n组辅助白噪声，辅助噪声是以正、负成对的形式加入的，从而生成两套集合IMF

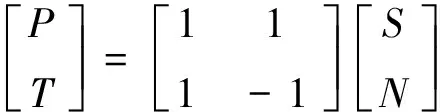
(3)

式中：S为原始信号；N为辅助噪声；P和T分别为加入正、负成对噪声后的信号。从而集合信号就为2n个。

(2)对集合中的每一个信号做EMD分解，每个信号得到一系列的IMF分量，其中第i个信号的第j个IMF分量为IMFij。

(3)然后对多组分量组合的方式求均值

(4)

1.3 小波软阈值去噪

小波阈值去噪的基本原理是设置一个临界阈值λ，若小波系数<λ，则该系数主要由噪声产生的，去除这部分系数；若小波系数>λ，则该系数主要是由信号产生的，保留这部分系数，最后对处理后的小波系数进行逆变换得到去噪后的信号。小波阈值去噪方法的步骤：

(1)将原始信号x(t)进行小波变换到小波域，得到一组小波分解系数。

(2)在小波域进行阈值处理后，得到压制主要包含随机噪声的较小的小波系数。

(3)利用处理后的小波系数进行信号重构，就得到去噪后的信号。阈值处理方法较多，本文使用的是软阈值方法，其阈值函数为

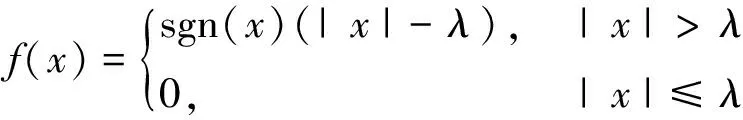
(5)

式中:sgn()为符号函数；λ为阈值。

1.4 利用3σ原则提取IMF1和IMF4的细节部分

由于IMF是从高频到低频排列的,一般情况下认为IMF1是高频噪声，就会将其舍去，但是IMF1中仍有信号的细节信息。而IMF4中含有低频噪声，也存在信号的细节信息，从而为了更好的重构去噪信号，需要进一步对IMF1和IMF4进行信噪分离。根据CEEMD的原理知，IMF1和IMF4满足加性噪声模型

IMF1=y1+n1

(6)

IMF4=y4+n4

(7)

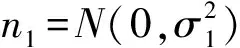
(8)

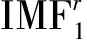
(9)

式中,HH1为IMF1的高频子带小波系数[13]。而噪声n4分布与n1恰相反，利用3σ原则对IMF提取细节部分表示为

(10)

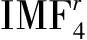
(11)

式中,HH4为IMF4的高频子带小波系数。

1.5 基于ICA-CEEMD小波阈值去噪

本文基于ICA-CEEMD小波阈值去噪方法具体步骤及流程图(见图1)。

(1)将一维含噪信号a等分成m段，然后平移拼接得到m维信号源作为Fast ICA的输入通道信号。

(2)将m维信号源经Fast ICA盲源分离得到初步去噪信S1号。

(3)再将S1信号利用CEEMD进行分解为四层IMF，利用频谱发现源信号波集中在IMF2和IMF3上，保留这两层IMF。

(4)利用3σ原则对IMF1和IMF4进行细节部分的提取，得到新的IMF1和IMF4，然后将IMF2和IMF3与新的IMF1和IMF4进行重构。

(5)利用小波软阈值对重构信号进一步降噪，提升降噪效果和性能指标。

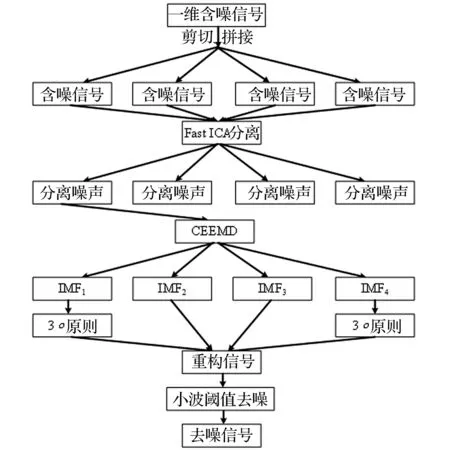
图1 本文方法框架图Fig.1 The frame diagram of the proposed method

2 仿真实验

本文实验所用软件为Matlab2010a，源信号为S=sin(2π·500 t)(振幅为1，频率为500 Hz)。根据微机电系统(MEMS)水听器在实际海水和湖水实验数据采集中，其会受到不同随机干扰而产生的高频噪声、低频漂移和突发的外力冲击影响。利用随机噪声所产生的整个频谱的噪声和低频漂移性来模拟水听器的高频噪声和低频漂移，利用脉冲噪声的突发性来模拟水听器所受到的突发外力冲击。对源信号加入不同的随机噪声和脉冲噪声，分别得到不同信噪比的噪声信号a。由于篇幅有限，本文以去噪前信噪比为4 dB的加噪信号进行说明，图2分别为源信号和加噪信号图及对应频谱图。

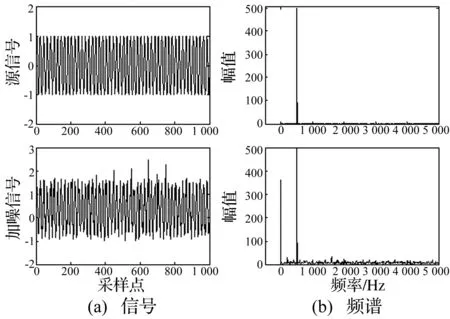
图2 源信号和加噪信号及其频谱Fig.2 Source signal and noise signal and its frequency spectrum

将含噪信号a分为四段，即a=[n1,n2,n3,n4]，然后将信号进行平移和拼接得到新的三个信号，即表示为a1=[n2,n3,n4,n1] 、a2=[n3,n4,n1,n2]、a3=[n4,n1,n2,n3]，其频谱不会发生变化，将该四路信号作为Fast ICA的输入通道信号(见图3)。

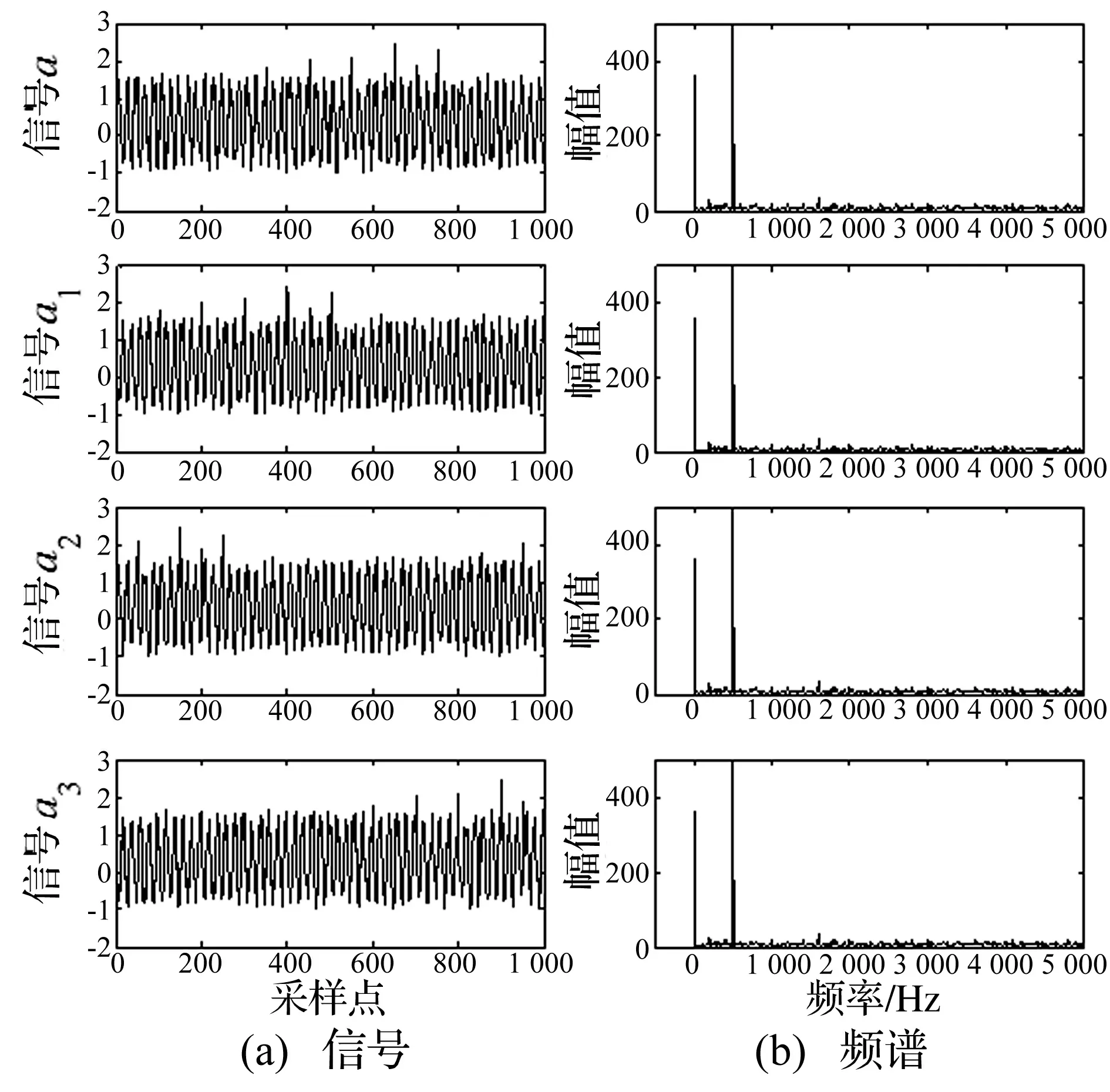
图3 Fast ICA输入通道信号及其频谱Fig.3 Fast ICA input channel signal and its spectrum

利用Fast ICA对信号进行初步的信噪分离，得到分离结果(见图4)。其中ICA1仍还有一部分噪声存在，而剩下的ICA2、ICA3和ICA4幅频谱在500 Hz处，幅值几乎为0，所以其都是分离的噪声。

图4 独立分量及其频谱Fig.4 Independent component and its spectrum

再利用CEEMD对分离得到独立分量信号ICA1进行分解重构(见图5)。将该信号分解为四层固有模态分量，从信号图及其幅频谱上可以看出，信号的能量基本集中在IMF2和IMF3上，而大部分噪声集中在IMF1和IMF4上。

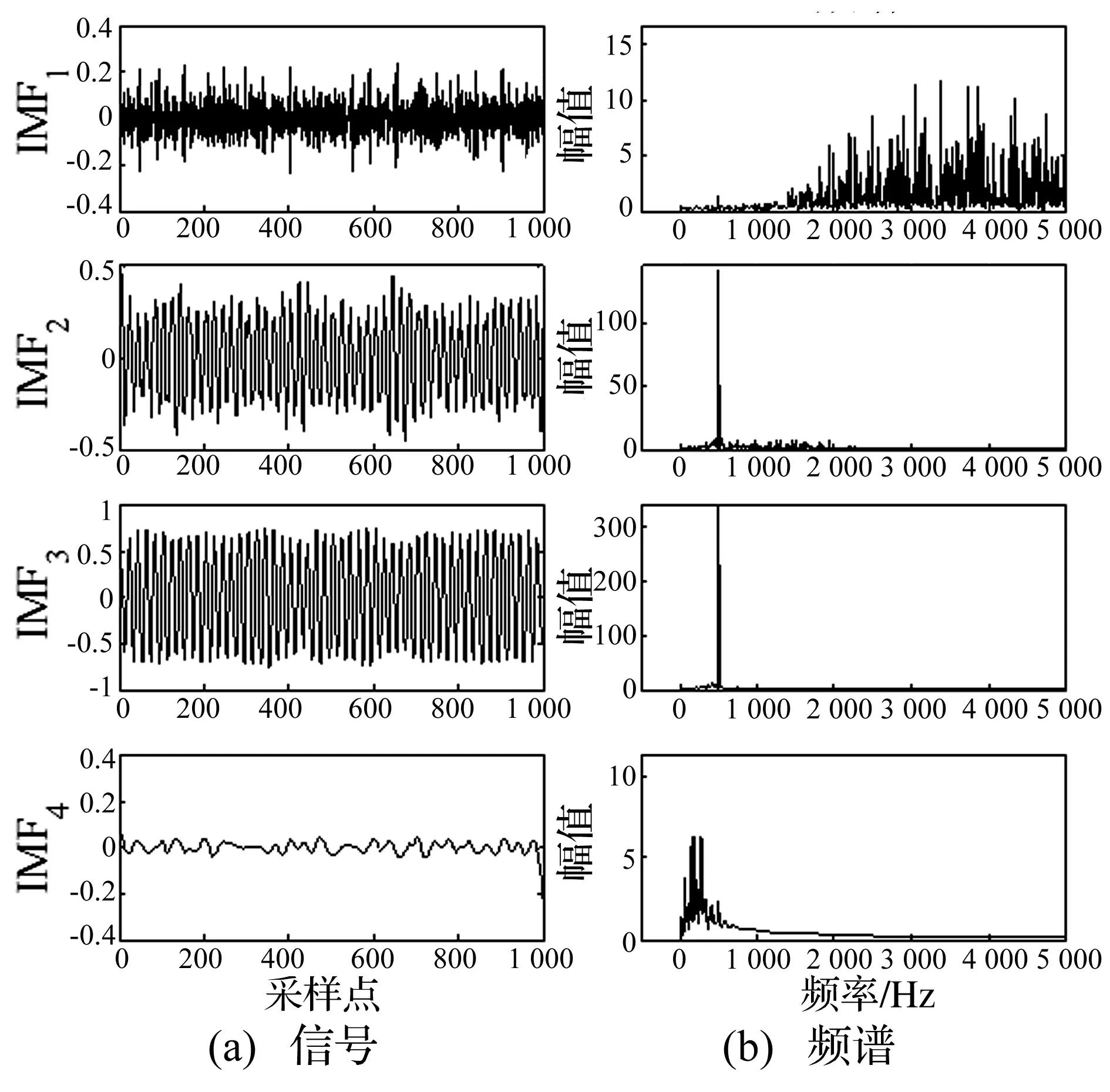
图5 CEEMD分解IMF及其频谱Fig.5 The IMF of CEEMD and its spectrum

利用3σ原则对IMF1和IMF4进行细节部分的提取，并与IMF2和IMF3进行信号重构，得到的重构信号再利用小波软阈值进一步降噪。去噪后并与小波阈值去噪和基于CEEMD的小波软阈值去噪进行对比(见图6)。

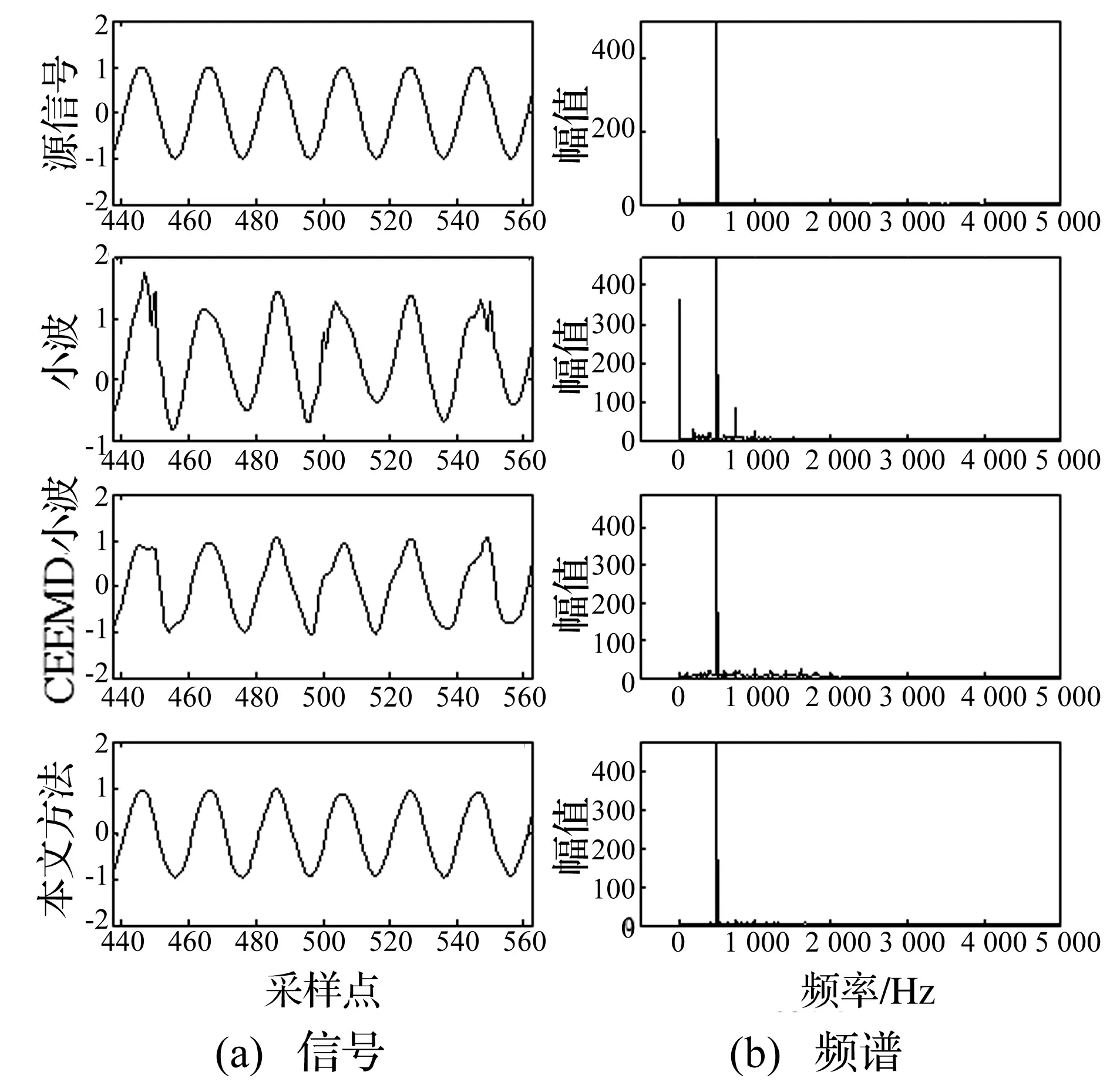
图6 源信号和降噪信号及其频谱Fig.6 Source and noise reduction signal and its spectrum

为定量说明本文方法的优越性，应用信噪比SNR和均方误差MSE来评价去噪效果。其对应的计算公式为

(12)

(13)

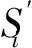
由图6、图7和表1可知本文算法的优越性和有效性，本文方法在去噪效果和性能指标上都明显优于小波阈值去噪和CEEMD小波去噪算法。

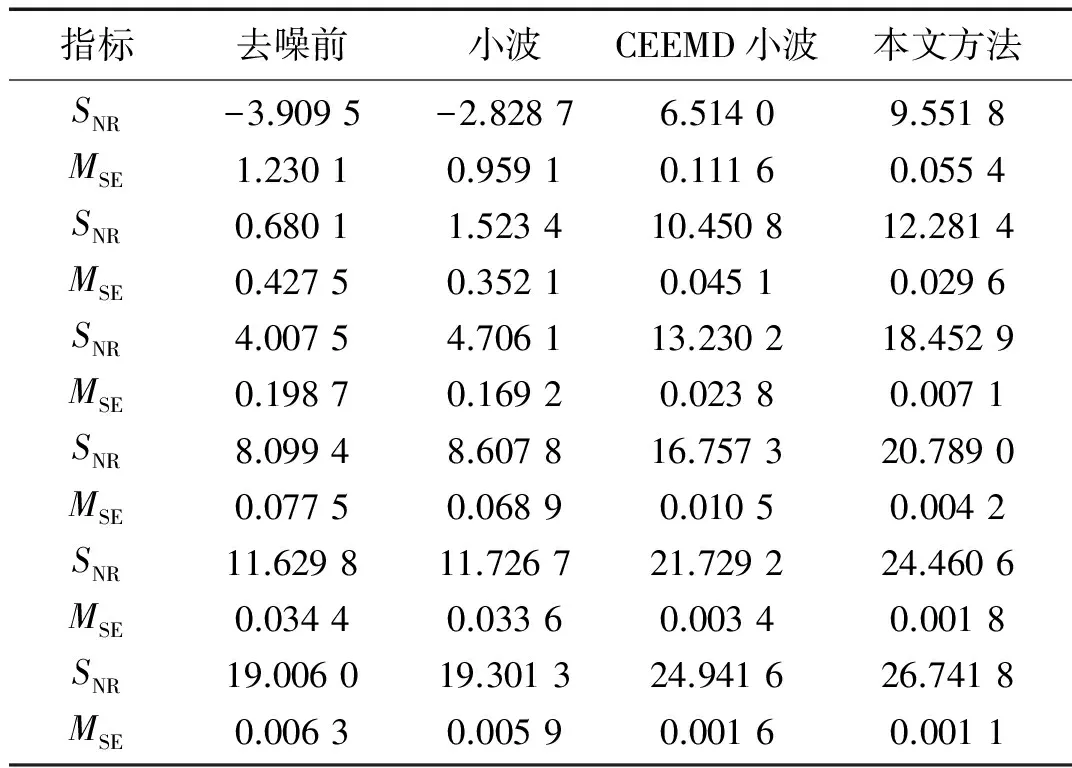
表1 性能指标数据对比

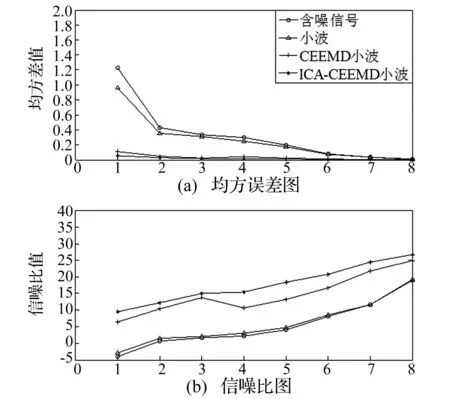
图7 均方误差和信噪比变化图Fig.7 The variation diagram of MSE and SNR

3 实测数据实验

由中北大学研制的MEMS矢量水听器(见图8)，是将MEMS技术应用于水听器技术的一种新的尝试。该水听器借鉴鱼的侧线感知系统，根据介观压阻效应和声学柱体的同振原理，以量子阱薄膜为敏感单元。其采用微纳结合的纤毛式水声矢量探测仿生结构声波引起纤毛式声学柱体的振动，使四梁微结构内部产生形变，导致纳机电敏感单元共振隧穿电流变化，产生介观压阻效应。通过检测系统提取电阻的变化，从而实现水下声信号的探测，由于微纳敏感结构可实现批量制造和一次性集成，所以MEMS 矢量水听器具有体积小、一致性好等特点，更适于组阵。MEMS 矢量水听器经中船重工715 所水声国防一级计量站标定测试，灵敏度达-184.6 dB(0 dB=1 V/μPa)，频率响应为5 Hz～5 kHz，且矢量水听器阵中的单分量矢量水听器具有良好的“8”字型余弦指向性[14]。

图8 中北大学研制的MEMS矢量水听器Fig.8 MEMS vector hydrophone is developed by the North University of China

中北大学微纳米技术研究中心在汾河二库进行了汾机实测实验，将水听器阵列(MEMS矢量水听器4元线阵，间距1 m)置于岸边固定，换能器置于拖船上，拖船离阵列距离逐步加大，选择不同位置抛锚不动，利用换能器发射信号，然后进行数据采集。

本文选取汾机500 Hz数据包进行实验处理，随机从第62 001～第63 000个截取四路信号(见图9)。

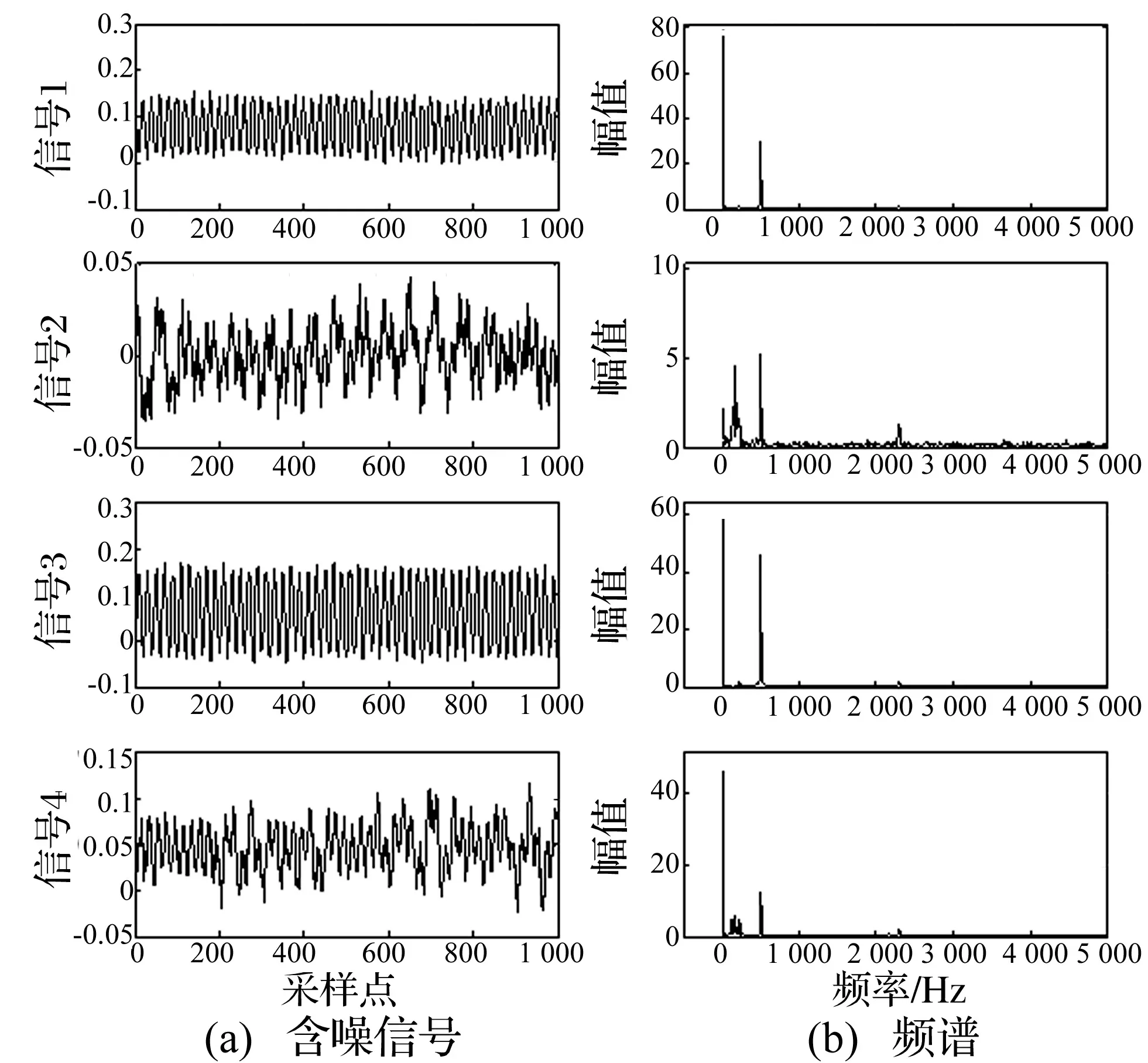
图9 采集的四路信号及其频谱图Fig.9 Four signals and their frequency spectra

利用本文方法对上述四路信号进行去噪处理(见图10)。去噪信号图和频谱图都显示出保留了源信号的余弦特征，并且消除了大部分噪声，去噪效果明显。

4 结 论

本文在ICA、CEEMD、3σ原则和小波阈值的基础上，提出了一种基于ICA-CEEMD的小波阈值去噪方法，通过对信号的剪切、平移、拼接得到ICA的输入通道信号，经ICA的初步信噪分离后，利用CEEMD对分离的信号进行分解，再应用3σ原则对第一个和最后一个IMF进行细节信息提取，然后进行信号的重构。最后，利用小波软阈值对重构信号进行去噪，提升去噪效果和性能指标。利用Matlab软件验证了该方法的有效性，并与小波阈值去噪和基于CEEMD小波阈值去噪做了对比实验。仿真实验和中北大学汾机实测实验结果都表明，本文方法在去噪效果和性能指标上都明显优于前两种方法，并表现出明显的有效性和实用性。

[ 1 ] 余先川，胡丹. 盲源分离理论与应用[M]. 北京：科学出版社，2011:1-14.

[ 2 ] 王祁. 传感器信息处理及应用[M]. 北京：科学出版社，2012:1-30.

[ 3 ] 梁斌，王鹏，白艳萍. 一种MEMS水听器信号去噪的组合算法研究[J]. 传感技术学报，2014，27(11)：1477-1481. LIANG Bin，WANG Peng，BAI Yanping. A combination algorithm for MEMS hydrophone signal and noise separation [J]. Chinese Joural of Senors and Actuators，2014，27(11)：1477-1481.

[ 4 ] 高云超. 希尔伯特-黄变换在水声信号处理中的应用研究[D]. 哈尔滨：哈尔滨工程大学，2009.

[ 5 ] 樊姣荣，王晓瑶，刘文怡,等.MEMS矢量水听器阵列信号处理研究[J]. 传感器与微系统，2012，31(1)：14-19. FAN Jiaorong，WANG Xiaoyao，LIU Wenyi，et al. Study on signal processing based on MEMS vector hydrophone array [J]. Transducer and Microsystem Technologies，2012，31(1)：14-19.

[ 6 ] 杨向林，严洪，许志,等. 基于Hilbert-Huang变换的ECG消噪[J]. 电子学报，2011，39(4)：819-824. YANG Xianglin，YAN Hong，XU Zhi，et al. ECG de-noising base on Hilbert-Huang transform [J]. Acta Electronica Sinica，2011，39(4)：819-824.

[ 7 ] 王文波，张晓东，汪祥莉. 基于主成分分析的经验模态分解消噪方法[J]. 电子学报，2013，41(7)：1425-1430. WANG Wenbo，ZHANG Xiaodong，WANG Xiangli.Empirical mode decomposition de-noising method based on principal component analysis [J]. Acta Electronica Sinica，2013，41(7)：1425-1430.

[ 8 ] CAO Junhong，WEI Zhuobin. Independent component analysis in frequency domain and its application in structural vibration signal separation [J]. Procedia Engineering，2011，16(3)：511-517.

[ 9 ] HUANG N E，SHEN Z，LONG S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society a Mathematical Physical & Engineering Sciences，1998，454：903-995.

[10] 郝凤龙，徐更光，黄学义.基于经验模态分解及小波变换的炸药NQR信号处理[J]. 振动与冲击，2014，33(16)：183-187. HAO Fenglong，XU Gengguang，HUANG Xueyi. Processing of explosive nuclear quadrupole resonance signals based on empirical mode decomposition and wavelet transform [J]. Journal of Vibration and Shock，2014，33(16)：183-187.

[11] WU Zhaohua, NORDEN E, HUANG. Ensemble empirical mode decomposition: a noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis，2009，1(1)：1-41.

[12] 王姣，李振春，王德营. 基于CEEMD的地震数据小波阈值去噪方法研究[J]. 石油物探，2014，53(2)：164-172. WANG Jiao，LI Zhenchun，WANG Deying. A method for wavelet threshold denoising of seismic data based on CEEMD [J]. Geophysical Prospecting for Petroleum，2014，53(2)：164-172.

[13] LEE Y H，RHEE S B. Wavelet-based image denoising with optimal filter [J]. International Journal of Information Processing Systems，2005，1(1)：32-35.

[14] 王鹏. 基于MEMS矢量水听器阵列的声目标定向定位技术研究[D]. 太原：中北大学，2013.

A method for sensor signal de-noising based on ICA-CEEMD wavelet threshold

HEBin，ZHANGYating，BAIYanping

(School of Science, North University of China, Taiyuan 030051, China)

A method for sensor signal de-noising based on ICA-CEEMD wavelet threshold was proposed for the separation of different noise and signal. The method was to carry out the shear segmentation, translation and mosaic of one-dimensional noisy signals, and obtain several different noisy signals as the channel signal for independent component analysis (ICA).The signal and noise were separated by the blind source separation of ICA. The separation signal was decomposed by the complementary ensemble empirical mode decomposition (CEEMD). Due to different high frequency and low frequency noise, the high order and low order intrinsic mode components (IMF) of the decomposition needed to be processed. The way of 3 sigma principle was used to extract the detail information of the first layer of IMFs and the final layer of IMFs, and restrain the mode mixing effects and reconstruct the signal of de-noising. Then, the wavelet threshold was used to deal with the reconstructed signal, so as to improve the de-noising effect and the performance index. In order to verify the validity of the method, the simulation experiment and the Fenji test of North University of China were carried out. The results show that the proposed method is better than the wavelet soft threshold de-noising and wavelet threshold de-noising method based on CEEMD.

ICA-CEEMD; wavelet threshold; sensor; de-noising; 3 sigma principle

国家自然科学基金(61275120)；山西省研究生教育创新项目(2016SY050)

2015-10-22 修改稿收到日期：2016-01-27

赫彬 男，硕士生，1988年生

白艳萍 女，博士，教授，博士生导师，1962年生

TN911.4;TP391

A

10.13465/j.cnki.jvs.2017.04.036