热环境对FGM壳模态频率的影响

刘文光， 舒 斌， 郭隆清， 贺红林

(南昌航空大学 航空制造工程学院,南昌 330063)

热环境对FGM壳模态频率的影响

刘文光， 舒 斌， 郭隆清， 贺红林

(南昌航空大学 航空制造工程学院,南昌 330063)

为了推动功能梯度材料(FGM)在高超音速飞行器热防护结构设计中的应用，旨在探讨不同温度场对热防护壳模态频率的影响，提供热防护壳动力学设计参考。从陶瓷金属基FGM的热物性参数模型入手，结合圆柱薄壳能量原理，建立FGM圆柱壳的模态方程。在此基础上，首先分析热物性参数变化规律对FGM壳模态频率的影响，然后探讨考虑热应力后不同热环境下FGM壳模态频率的变化规律。结果表明，FGM物性参数变化对模态频率的影响没有热力耦合影响明显；温度梯度<300 K时，物性参数变化对模态频率起主导作用，反之温度梯度>300 K时，热应力和热变形对模态频率起主导作用。

热环境；热防护系统；功能梯度材料；模态频率

高超音速飞行器飞行时，因空气黏性作用与物面边界层内的气流会产生强烈的摩擦，使气流动能转化为热能，造成壁面附近温度急剧升高，高温空气不断向低温壁面传热，引起很强的气动加热。而且，随着飞行马赫数越大，飞行器表面的气动加热程度将越严重，其表面外形、结构强度和刚度也将随之改变，直接危及飞行安全。例如，哥伦比亚号航天飞机在再入大气层时，因气动摩擦产生了1 400°的高温气体，该气体穿透左机翼损伤部位后融化了内部结构，致使机翼和机体融化，导致航天飞机解体。研究表明，气动加热问题的机理十分复杂，它不仅与高超音速飞行器的速度、高度、附面层状态有关，而且直接影响飞行器结构的动力学特性[1]。因此，高超音速飞行器要合理设计热防护系统，尤其要了解防护结构的强度、刚度以及气动加热对结构动力学特性的影响。

热防护系统不仅要求安全和重量轻，而且还要求保护机身结构、材料具有低催化反应性，同时要求系统结构能适应变形和承受热力载荷，能经受飞行时的气动压力变化。于是有学者试图把功能梯度材料(Functionally Graded Material，FGM)应用于高超音速飞行器的热防护系统结构。因高超音速的气动加热问题，使得热环境下FGM结构的振动分析成为学术界与工程界的研究热点，尤其是FGM板壳的振动问题。例如，基于一阶剪切变形理论，MOKHTAR等[2]研究了FGM板的热振动现象，SHUKLA等[3]研究了温敏FGM矩形板的动力响应；PRAVEEN等[4]结合有限元方法分析了FGM板的非线性瞬态热弹性动力学响应；ZHAO等[5]采用无网格法探讨了温敏FGM板的自由振动。为考虑非线性影响，HUANG等[6]基于高阶剪切变形理论研究了热力环境下FGM板的动态响应；KIM[7]研究了热环境下有预应力作用时FGM板的振动特性；SUNDARARAJAN等[8]运用冯卡门假设的非线性公式，分析了均匀温度场下温敏FGM板的自由振动；YANG等[9]研究了有初应力的温敏FGM板的动响应以及均匀热变化条件下的热效应。滕兆春等[10]用微分求积法计算了温度影响下FGM圆环板面内自由振动的无量纲频率，以及均匀升温和非均匀升温两种情况下几何参数、材料性质和温度变化对面内自由振动频率的影响。

尽管研究者对FGM板的动力学问题做了一系列的工作，但是多数研究还仅停留于只考虑材料物性参数随温度影响下的振动分析，很少涉及热应力和热变形对FGM壳振动特性的影响。结合FGM在热防护系统上的应用前景以及圆柱壳是高超音速飞行器上的重要构件之事实，本文在探讨热物性参数变化对FGM壳模态频率影响之基础上，着重讨论热应力对FGM壳模态频率的影响规律，为热防护结构动力学设计提供理论支撑。

1 基本理论

1.1 FGM的热物性参数模型

如图1所示的陶瓷-金属基FGM模型，其体积分数逐渐变化使FGM的性能在厚度方向上呈渐变形式，顶面和底面材料分别为纯陶瓷和纯金属，中间为陶瓷基向金属基的逐渐变化部分。

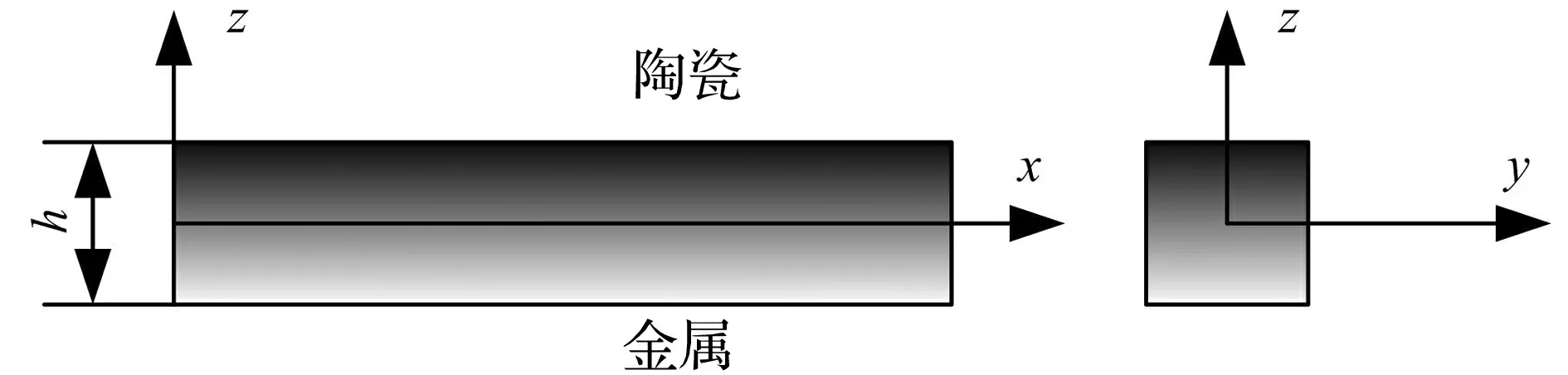
图1 功能梯度材料的模型及坐标系Fig.1 The model and coordinate of the FGM

建立图1所示的直角坐标系，为描述FGM的热物性参数随温度的变化规律，通常用幂函数公式来描述FGM物性参数沿厚度方向的变化

Γ(z,T)=

(1)

式中：Γ为FGM的弹性模量E、泊松比ν、密度ρ和热膨胀系数α等的属性；下标C和M分别为纯陶瓷和纯金属；z为厚度方向的坐标；N为体积分数指数；h为FGM板厚。

考虑在温度影响下FGM的物性参数变化规律为非线性，即

(2)

式中：λ为FGM的物理属性;T为环境温度;λi为组成材料特有的温敏材料属性；T0为室温(常取300 K);△T(z)为温差只沿厚度方向变化。

为便于分析FGM热物性参数的变化规律，表1给出了Si3N4/SUS304材料组份的温敏系数[11]。

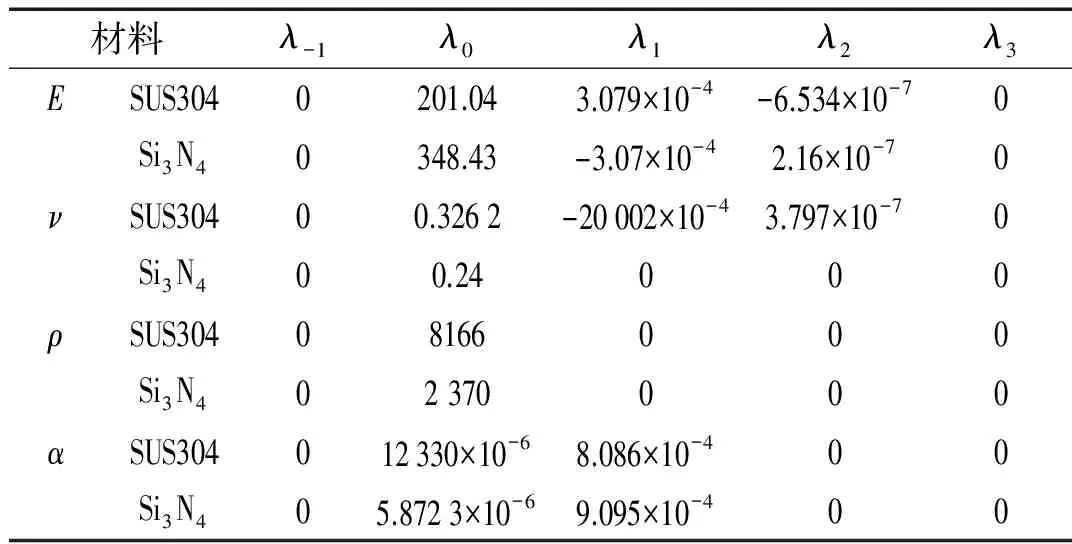
表1 Si3N4/SUS304温敏系数

1.2 圆柱壳的模态方程

如图2所示，高超音速飞行器热防护系统结构简化为FGM圆柱薄壳，薄壳的几何参数为：平均半径R、厚度为h、长度L。假设x，θ和z分别为壳的轴向、周向和径向坐标，在壳体的中面上建立正交坐标系(x,θ,z)，即壳体中面的轴向、周向和径向的位移分别为u，v和w。

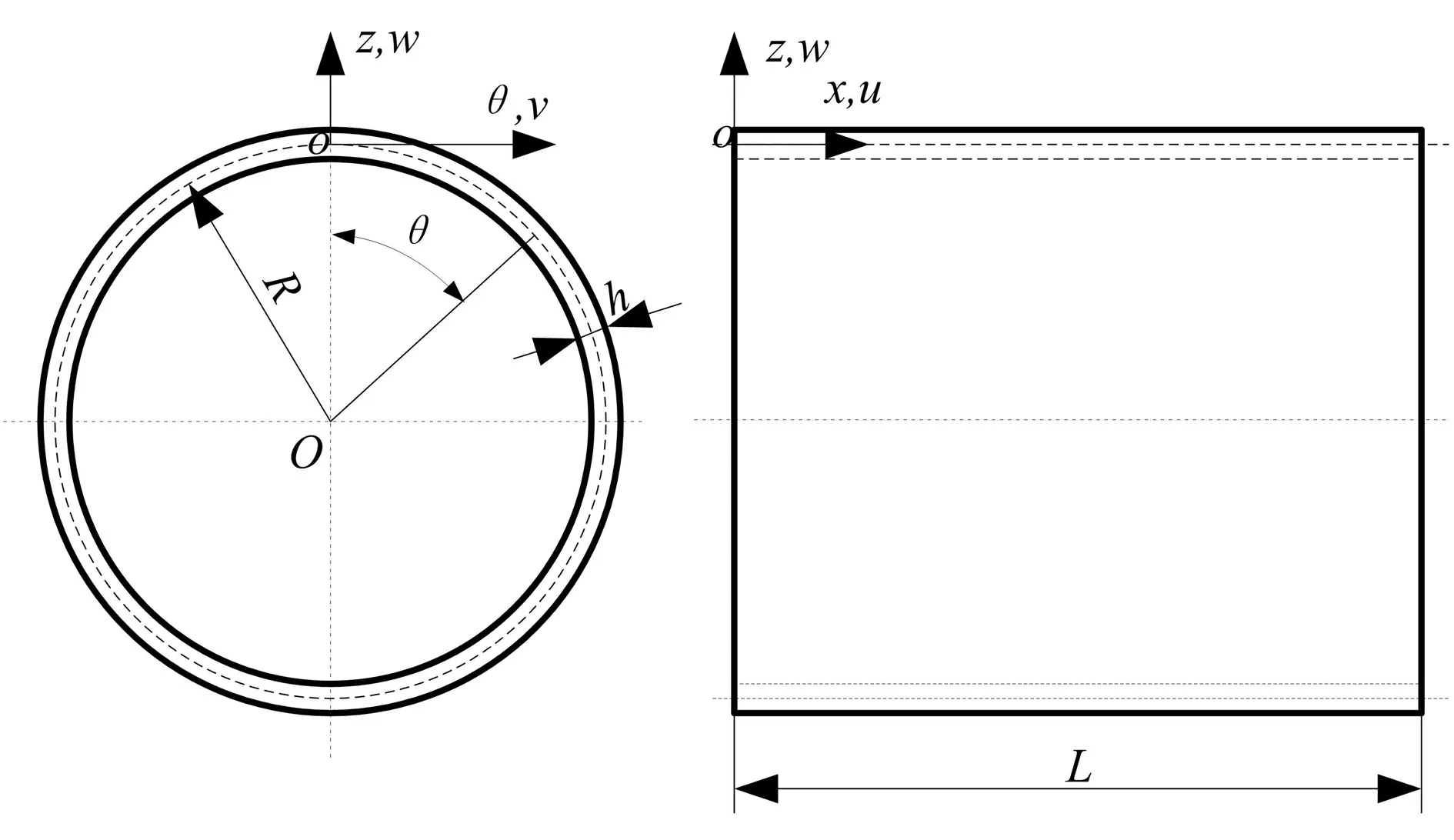
(a) (b)图2 热防护系统FGM圆柱壳简化几何模型Fig.2 Simplified geometry model of a FGM cylinder shell for the thermal protection system

圆柱壳的应变能为[12]

2B11e11κ11+2B12(e11κ22+e22κ11)+

(3)

式中：e11，e22和e12为参照曲面的应变;κ11，κ22和κ12为参照曲面的曲率;Aij，Bij和Dij(i,j=1,2,6)分别为薄膜刚度、耦合刚度和弯曲刚度。

不计转动惯量，圆柱壳的动能为

(4)

式中：t为时间;ρ为密度。

假设位移u,v和w函数形式为

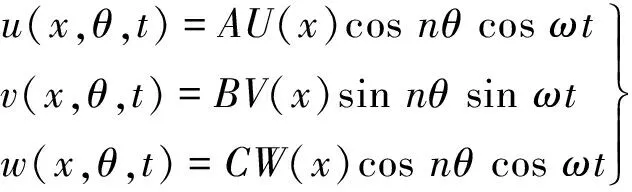
(5)

式中：A、B、C为振幅；U、V、W为振型函数;n为圆周波数;ω为角频率。

结合方程式(5)和最小能量原理，得到Lagrange函数表达式

F=Tmax-Smax

(6)

式中,Tmax和Smax分别为最大动能和最大应变能。

取Lagrange函数关于振幅A，B，C的极值，可得到用于确定圆柱壳的模态频率和模态振型的特征方程

(7)

式中,矩阵元素dij取决于圆柱壳的几何参数和几何边界条件。

2 热环境对FGM壳固有频率的影响

FGM在热环境下其力学性能会受物性参数变化的影响，结构刚度和强度也随之改变。同时，FGM因受热不均或热变形受到约束时，圆柱壳内部会产生热应力，形成非线性刚度矩阵，进一步影响结构刚度和强度。本文首先分析均匀温度场下FGM物性参数变化对FGM壳的模态频率的影响，然后综合考虑热物性参数变化与热力耦合，研究FGM壳模态频率的变化规律。

2.1 热物性参数变化对FGM壳模态频率的影响

为简化分析，忽略热防护壳外表面与流动空气的接触对模态频率的影响，并假定FGM壳的四边均为固支边界条件。计算时取FGM热防护壳的几何参数为：θ=0.1 rad，L=0.2 m，R=6 m，h=0.001 5 m。为考虑均匀温度对FGM物性参数的影响，依次分析了温度为300 K、500 K、600 K和800 K时FGM壳的各阶次模态频率，结果见图3。

图3 均匀温度场下模态频率随体积分数的变化Fig.3 The modal frequency vs. volume fraction under the uniform temperature field

分析发现，FGM壳模态频率随体积分数指数N值的增大而减小，同一均匀温度场环境下，高阶模态频率随体积分数指数N值的变化程度更为显著。

2.2 热应力对FGM壳模态频率的影响

为模拟表达高超音速飞行器热防护壳的气动加热过程，假设FGM壳的温度边界条件为：壳体内表面温度值为300 K，FGM壳体外表面的温度区间为400～1 000 K。同理，假定FGM壳为四边固支边界条件。计算时取FGM壳的几何参数为：θ=0.157 rad，L=0.6 m，R=6 m，h=0.004 5 m。

为对比均匀温度场和温度梯度场两类热环境对FGM模态频率的影响规律，依次分析了体积分数指数值N=0.1条件下外表面温度从400 K升高至1 000 K热力耦合环境下的FGM壳模态频率值，结果见图4。

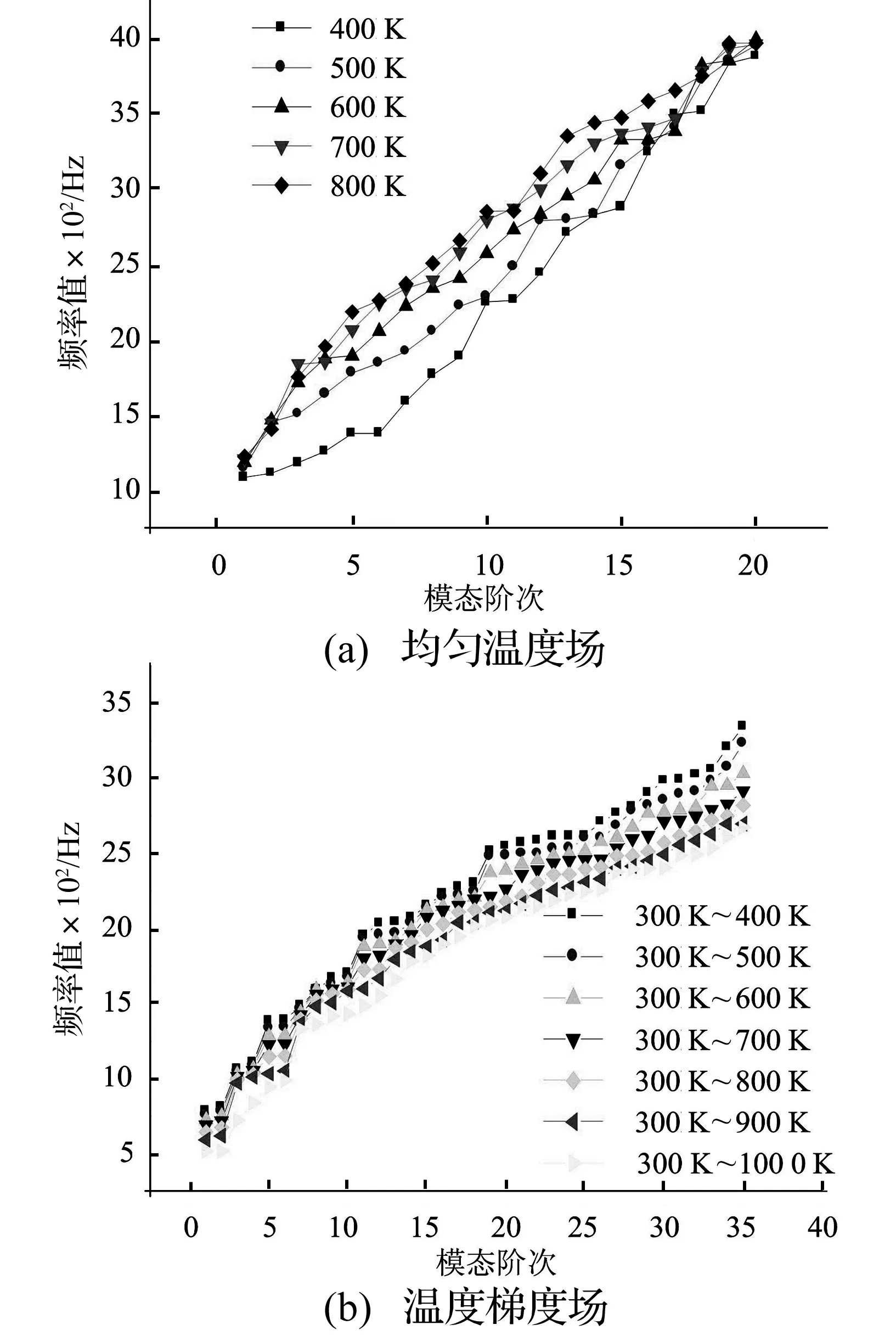
图4 计热应力后温度场对模态频率的影响Fig.4 Impacts of temperature field on the modal frequency with thermal stress

分析发现，均匀温度下考虑热应力后FGM壳的模态频率明显增大，第一阶模态频率变化较小，但随着模态阶次的升高模态频率值变化率是先增大后减小。原因在于，虽然温度升高，FGM的弹性模量和泊松比下降使结构模态频率减小，但是温度升高后热应力产生的正刚度大于因弹性模量和泊松比下降而引起的负刚度，从而使FGM壳的振动模态频率略有增加。进一步分析发现，当温度T>600 K后，随着温度的升高，相同各阶次模态频率的增幅开始减小，即均匀温度达到一定值后，各阶次模态频率的影响逐渐减弱。相反，线性温度梯度下，热力耦合时FGM壳的模态频率下降明显，而且随着线性温度梯度区间范围的增大，越高阶模态的频率值随温度增加下降的速率有所增强。研究表明，和单纯的物性参数变化对模态频率的影响不同，由于热应力和热变形综合影响，相同阶次模态频率随着线性温度梯度环境变化FGM壳的模态频率值有同频情况。

为进一步探讨各种热环境对FGM壳模态频率值的影响，表2设计了几种不同的工况，并针对这几种工况进行了分析。

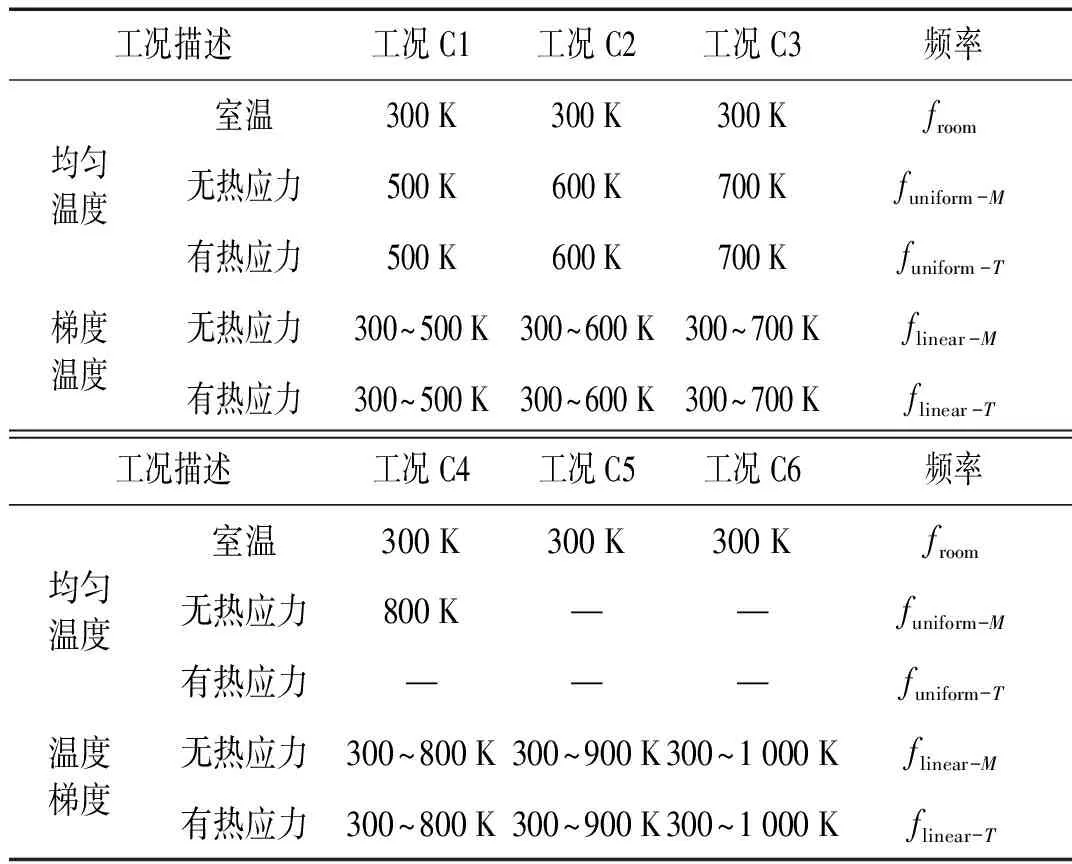
表2 计算工况的温度设置

结果表明，高温对FGM壳模态频率的总体影响是使其值减小，室温环境下模态频率值最大，在加载均匀温度场时，FGM壳的模态频率最小，如图5所示。

研究发现，各模态频率曲线之间的间距随模态阶次升高越来越大，即随着梯度温度差的增大，温度环境下热力耦合对结构模态频率的影响越来越大。结论表明，当陶瓷面温度在700 K以下时，均匀温度场环境下，考虑热应力后的FGM壳模态频率最小。同阶次模态频率的大小关系为

froom>flinear-M>funiform-M>flinear-T>funiform-T

当陶瓷面的温度在800 K以上时，同阶次模态频率的大小关系为

froom>flinear-M>funiform-M>flinear-T

分析表明，FGM物性参数变化对结构模态频率的影响没有热力耦合共同的影响大，线性温度场条件下的FGM壳模态频率比室温环境小。

因此，为保证高超音速热防护系统具有足够的强度，进行动力学设计时必须考虑热应力对结构模态频率的影响。

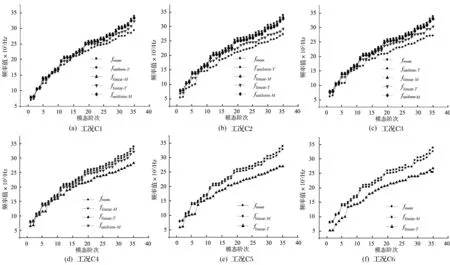
图5 不同热环境对模态频率的影响Fig.5 Impacts of thermal environment on the modal frequency with thermal stress

3 结 论

以高超音速飞行器热防护FGM圆柱壳为研究对象，通过高温结构热力耦合壳体理论和FGM温敏特性相融合，研究了多种温度场下FGM壳模态频率的变化规律，得到以下主要结论：

(1)考虑热力耦合后FGM壳的模态频率比单纯考虑材料物性参数变化影响下的相同阶次模态频率大；温度越高两条曲线之间的间隔越大，说明均匀温度场环境产生的热应力对结构的模态频率起主导作用。

(2)随着温度梯度区间的增加，FGM壳的物性参数如弹性模量等逐渐下降，而且弹性模量和泊松比的下降导致FGM壳的刚度下降，进而导致FGM壳模态频率不断下降。

(3)线性温度场下，当金属面和陶瓷面两端的温差△T<300 K时，物性参数变化对壳模态频率起主导作用；反之，当金属面和陶瓷面两端的温度△T>300 K时，热应力和热变形对壳模态频率起主导作用。

(4)功能梯度材料的物性参数变化、热应力和热变形综合影响着结构的模态频率。

[ 1 ] 李海燕,唐志共,杨彦广,等.高超声速飞行器高温流场数值模拟面临的问题[J].航空学报, 2015,36(1): 176-191. LI Haiyan, TANG Zhigong, YANG Yanguang, et al. Problems of numerical simulation of high-temperature gas flow fields for hyper-sonic vehicles [J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1):176-191.

[ 2 ] MOKHTAR B, ABEDLOUAHED T, ABBAS A, et al. Buckling analysis of functionally graded plates with simply supported edges [J]. Leonardo Journal of Sciences, 2009, 8(15):21-32.

[ 3 ] SHUKLA K. Nonlinear static and dynamic analysis of functionally graded plates[J]. International Journal of Applied Mechanical and Engineering, 2006, 11 (3): 679-698.

[ 4 ] PRAVEEN G, REDDY J. Nonlinear transientthermo-elastic analysis of functionally graded ceramic-metal plates[J].International Journal of Solids and Structures, 1998, 35(33): 4457-4476.

[ 5 ] ZHAO X, LEE Y, LIEW K. Free vibration analysis of functionally graded plates using the element-free Kp-Ritz method [J]. Journal of Sound and Vibration, 2009,319(3/4/5):918-939.

[ 6 ] HUANG X, SHEN H. Nonlinear vibration and dynamic response of functionally graded plates in thermal environments [J]. International Journal of Solids and Structures, 2004, 41(9/10): 2403-2427.

[ 7 ] KIM Y. Temperature dependent vibration analysis of functionally graded rectangular plates [J]. Journal of Sound and Vibration, 2005,284 (3/4/5): 531-549.

[ 8 ] SUNDARARAJAN N, PRAKASH T, GANAPATHI M. Nonlinear free flexural vibrations of functionally graded rectangular and skew plates under thermal environments [J]. Finite Elements in Analysis and Design, 2005, 42 (2):152-168.

[ 9 ] YANG J, SHEN H. Vibration characteristics and transient response of shear-deformable functionally graded plates in thermal environments [J]. Journal of Sound and Vibration, 2002, 255(3): 579-602.

[10] 滕兆春,蒲育.温度影响下FGM圆环板的面内自由振动分析[J]. 振动与冲击, 2015, 34(9):210-217. TENG Zhaochun, PU Yu. In-plane free vibration of FGM annular plates considering temperature effect [J]. Journal of Vibration and Shock, 2015, 34(9): 210-217.

[11] ALIJANI F, BAKHTIARI N, AMABILI M. Nonlinear vibrations of FGM rectangular plates in thermalenvironments [J]. Nonlinear Dynamics, 2011, 66(3): 251-270.

[12] 王宇,罗忠.薄壁圆柱壳构件受迫振动的响应特征研究[J]. 振动与冲击, 2015,34(7):103-108. WANG Yu, LUO Zhong. Study on response characteristics for forced vibrations of thin cylindrical shell [J]. Journal of Vibration and Shock, 2015, 34(7): 103-108.

Impacts of thermal environment on modal frequency of FGM shells

LIUWenguang，SHUBin，GUOLongqing，HEHonglin

(School of Aeronautic Manufacturing Engineering, Nanchang Hangkong University，Nanchang 330063，China)

In order to promote the application of functionally graded materials (FGMs) in the structure of thermal protection systems, the aim of this work is to study the impacts of different temperature fields on the modal frequencies of thermal protection shells and to provide some methods for dynamical design of hypersonic aircrafts. Starting from the thermal-physical property model of the ceramic and metal based FGMs, the modal frequency equation of an FGM shell was derived by using the energy principle. Thereafter, the impacts of the change law of thermal physical properties on modal frequencies were analyzed. And the change law of modal frequency of the FGM shell with thermal stress was discussed under different thermal conditions. Results indicate that the impacts of the change of physical properties on the modal frequency are less than that of thermal-mechanic coupling on the modal frequency. The change law of physical properties plays a main role on modal frequency when the temperature grade below 300 K while the thermal stress and strain plays a main role when the temperature grade above 300 K.

thermal environment; thermal protection system; functionally graded material; modal frequency

国家自然科学基金项目(51565039)

2015-10-20 修改稿收到日期：2016-01-12

刘文光 男，博士,副教授，1978年5月生

V215.4

A

10.13465/j.cnki.jvs.2017.04.020