机电液系统动能刚度图示化在线识别技术

杨 彬， 谷立臣,2， 刘 永,3

(1.长安大学 公路养护装备国家工程实验室，西安 710064；2.西安建筑科技大学 机电工程学院，西安 710054； 3.湖北汽车工业学院 机械工程学院，湖北 十堰 442002)

机电液系统动能刚度图示化在线识别技术

杨 彬1， 谷立臣1,2， 刘 永1,3

(1.长安大学 公路养护装备国家工程实验室，西安 710064；2.西安建筑科技大学 机电工程学院，西安 710054； 3.湖北汽车工业学院 机械工程学院，湖北 十堰 442002)

为在线检测机电液系统动能刚度，评价动力源与负载之间的功率匹配特性，提出利用李萨如图进行信息融合的动能刚度图示化识别方法。根据电机拖动液压系统的动力学模型，分析了系统的节能原理、动能刚度的物理意义及其对机电液系统功率的影响机理。再结合信号调制与信息融合技术，将系统的转矩、转速以及压力、流量信号融合成李萨如图形，通过检测图形特征的变化可以实现对系统动能刚度的在线识别。理论与实验研究结果表明：机电液系统动能刚度的变化是参数相互耦合的结果，可用于衡量动能变化率，评价系统的节能效果；融合的李萨如图形倾角可量化动能刚度大小，倾角变化反应了动能刚度的变化规律，由此得到的刚度圆能够评价系统动力源与负载之间的功率匹配性与在线运行状态。

机电液系统；动能刚度；功率匹配；图示化识别；信息融合

电动机拖动液压泵是机电液系统中最常见的动力源，以其响应速度快、输出平稳、高性能以及易于远程操作等优点，被广泛应用于各种液压设备中。随着自动化与智能化水平的提高，功率的传递越来越大，信息的传递愈加复杂，系统节能控制与功率匹配成为研究的热点和技术性难题。

理论与大量试验证实，系统的节能控制能够有效提高动力源与负载之间的功率匹配性，减小系统能耗，提高设备寿命与可靠性[1-3]。文献[4]提出动能变化率对设备的输入功率产生重要影响，降低动能变化率能够有效提高系统的节能效果。但由于缺乏评价动能变化率的有效方法，为开展控制降低动能变化率以提高节能效果的研究带来了难度。系统动态刚度是系统在特定动态激扰下抵抗变化的能力，以往对于动态刚度的研究主要以提高系统的鲁棒性为目的，国内外学者对此进行了大量研究[5-10]。然而，由于缺少合适的刚度检测手段，这在一定程度上不仅制约了刚度在系统功率匹配、状态监测以及节能控制方面的应用，也限制了对刚度物理意义的理解。

本文提出通过动能刚度衡量系统动能的变化率，以达到评价动力源与负载匹配性的目的。利用信号调制与信息融合技术，将电机的输出转速、转矩，液压泵的输出流量、压力，液压马达的输出转速、转矩融合成李萨如图，通过测量李萨如图特征量——倾角的大小，量化系统的动能刚度，为在线检测系统运行状态、客观评价系统节能效果提供了新的方法与思路。

1 机电液系统功率模型

1.1 机电液系统节能原理

利用二端口网络对机电液系统的能量转换过程进行描述[11]，如图1所示。

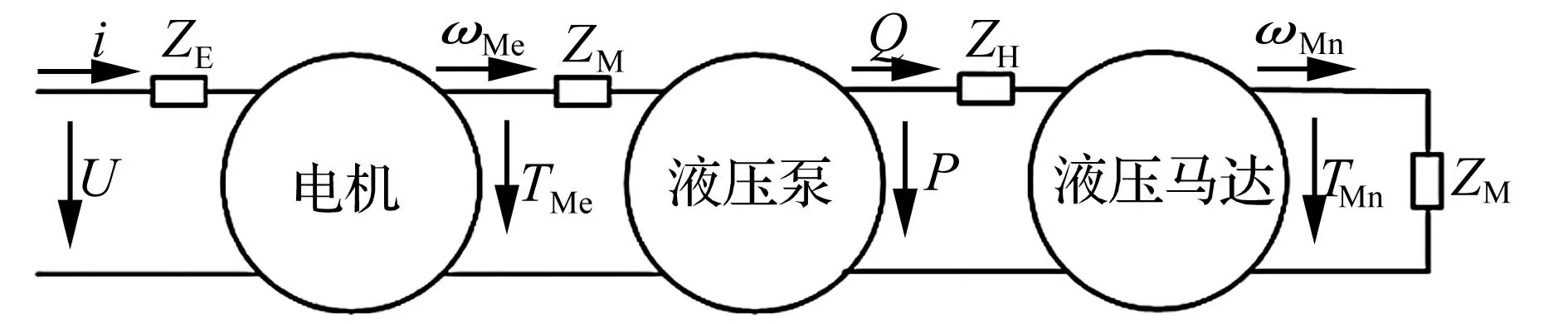
图1 机电液系统能量转换二端口网络模型Fig.1 Two-port network model of energy conversion for the mechanical electro-hydraulic system

机电液系统在运行过程中，伴随着电能、液压能以及机械能的相互转换和耦合。电机吸收电网的电能，经电磁、机电能量转换，输出机械能(转矩TMe、转速ωMe)拖动液压泵，液压泵作为机液能量转换元件，将电机输出的机械能转换为压力能(压力P、流量Q)驱动液压马达带载工作，液压马达将液压泵输出的液压能转换为机械能(转矩TMh、转速ωMh)输出。在系统能量传递过程中，还存在电气能量损失(电气阻抗ZE)、液压能量损失(液阻抗ZH)以及机械能量损失(机械阻抗ZM)。

如图1所示，在机电液系统能量转换过程中，系统输入功率主要以实际输出功率、损失功率、储备功率以及动能变化率四种形式存在，即

(1)

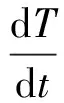
由式(1)可知，系统动能变化率小，则系统的输入功率降低。尤其在设备启停、作用冲击负载等工况时，动能变化率较大，导致系统功率输入较高，节能效果较差，因此工程上常采用蓄能器或变惯量装置等，回收或释放冲击能量，延长响应时间，以降低动能的变化率。下面从系统功率平衡的角度出发，结合动力学模型，研究动能变化率对机电液系统功率的影响规律。

1.2 机电液系统功率平衡方程

(1) 电机功率平衡方程

三相静止坐标系下的异步电机模型是典型的高阶、非线性、强耦合的多变量系统，通过坐标变换对异步电机模型进行降阶解耦处理。忽略空间谐波、磁路饱和、铁心饱和；假设三相绕组对称，磁动势沿气隙周围按正弦规律分布，各绕组的自感和互感恒定；不考虑频率变化和温度变化对绕组电阻的影响。在M-T坐标系下，异步电机数学模型由电压方程和转矩平衡方程组成[12]。

电压方程为

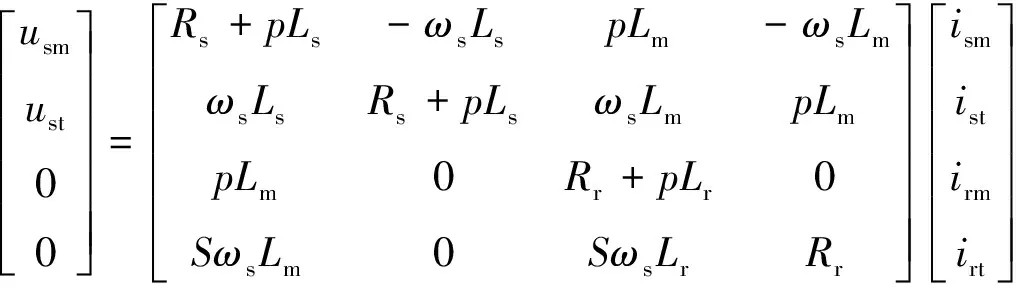
式中:Usm、Ust为定子M轴、T轴电压；Rs为定子绕组阻值；Rr为转子绕组阻值；Ls为定子绕组自感；Lr为转子绕组自感；Lm为定转子绕组互感；ωs为同步转速；S为转差率；ism、ist为定子M轴、T轴电流；irm、irt为转子M轴、T轴电流。

式(2)可简化为

u=Ri+Lpi+Gωsi

(3)

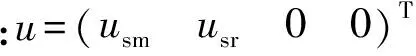
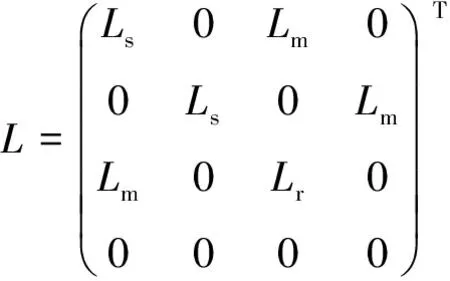
对式(3)两端同时乘iT可得

iTu=iTRi+iTLpi+iTGωsi

(4)

转矩平衡方程为

(5)

(6)

式中:np为极对数；Te为电磁转矩；Jt为折合到电机轴上的转动惯量；Bt为折合到电机轴上的阻尼；Kt为电机-泵联轴器扭转刚度；θr为电机输出角位移；θp为泵输入角位移；Tr=Lr/Rr为电机转子回路时间常数。

对式(5)两端同时乘机械角速度ωr/np可得

(7)

由式(4)和式(7)可得电机的功率平衡方程

(8)

(2)液压泵功率平衡方程

假设连接管道很短，忽略管道的压力损失；泵的泄漏流态为层流；不考虑液压泵的流量与压力脉动，则液压泵的数学模型由流量连续性方程和力矩平衡方程组成。

液压泵的流量连续性方程为

(9)

式中:Qp为液压泵的输出流量；Dp为液压泵的排量；ωp为泵输入转速；Cip为泄漏系数；Pp为液压泵高压腔压力；Vp为泵高压腔体积；βe为油液体积弹性模量。

对式(9)两端同时乘Pp，可得

(10)

力矩平衡方程为

(11)

式中:Jp为泵的转动惯量；Bp为黏性阻尼系数。

对式(11)两端同时乘泵输入转速ωp可得

(12)

联立式(10)、式(12)可得液压泵的功率平衡方程

(13)

(3)液压马达功率平衡方程

根据液压马达流量连续性方程与力矩平衡方程可得其功率平衡方程为

(14)

式中:Dm为液压马达的排量；ωn为马达输出转速；Cim为泄漏系数；Pp为液压马达高压腔压力；Vm为马达高压腔体积；Jm为泵的转动惯量；Bm为黏性阻尼系数；TL为作用在马达轴上的任意外负载。

(4) 机电液系统功率平衡方程

联立式(8)、式(13)、式(14)，可得机电液系统功率平衡方程为

(15)

由式(15)可知，系统动能变化率由电机、液压泵以及液压马达子系统的动能变化率组成，其运行状态改变是环境工况作用于系统的结果。因此各子系统的动能变化率的变化根据激扰源不同均可分为两部分:一部分为动力源输入变化而引起的动能变化;另一部分为负载变化导致的子系统动能变化。定义各子系统动能抵抗负载变化的能力为逆向刚度，抵抗动力源输入变化的能力为正向刚度。逆向刚度越大，则系统抗负载冲击的能力越强，动能变化率越小；正向刚度越大，则系统响应速度延长，动能变化率越小。逆向刚度与正向刚度共同组成了系统的动能刚度。下面通过建立机电液系统动力学模型，研究系统内部参量对动能刚度的影响机理。

2 机电液系统动能刚度

2.1 电机转速刚度

对式(2)～式(6)进行拉式变换，联立可得

(16)

由式(16)可得电机的速度刚度表达式

(17)

由式(17)可知，电机转速刚度由逆向刚度与正向刚度组成。电机转动惯量和阻尼越大，电机极对数越少，逆向刚度越大，反之，则越小。正向刚度受转动惯量、阻尼、转子绕组自感、转子回路时间常数、极对数、定转子绕组互感、转差率的影响，正向刚度越大，电机在启停或转速阶跃变化时，动能变化率较小，输出平稳。

2.2 液压泵流量刚度

对式(9)进行拉式变化，可得

(18)

由式(18)可得液压泵的流量刚度表达式

(19)

由式(19)可知，泵的流量刚度由逆向刚度与正向刚度组成。泵的泄漏量越小、体积弹性模量越大，则逆向刚度越大，反之，则越小；泵排量越小，则正向刚度越大，反之，则越小。刚度的大小随液压系统参量动态变化。

2.3 液压马达转速刚度

对液压马达的流量连续性方程以及力矩平衡方程进行拉式变化，联立可得

(20)

由式(20)可得液压马达的动态速度刚度表达式

(21)

由式(21)可知，马达的转速刚度由逆向刚度与正向刚度组成。马达的排量、转动惯量、体积弹性模量以及黏性阻尼越大，马达的泄漏量越小，则逆向刚度越大，反之，则越小。泄漏量、黏性阻尼、马达排量和转动惯量越大，体积弹性模量越小，则正向刚度越大，反之，则越小。刚度的大小随系统参量动态变化。

2.4 机电液系统刚度

由式(16)、式(18)、式(20)可得机电液系统动能刚度表达式

(22)

由式(22)可知，系统的正向刚度由各子系统正向刚度组成，是机电液系统内部参量相互耦合的结果，其大小主要受泵和马达排量以及各子系统转动惯量、阻尼、液压系统泄漏和油液体积弹性模量影响。负载工况或动力源输入的主动变化，必会导致系统内部参量的改变，因此系统的动能刚度随工况改变而动态变化。正向刚度增强，则系统动能变化率减小，输出平稳，节能效果好；逆向刚度减弱，则系统抗冲击抗扰动能力降低，动能变化率增大，系统能耗增大。因此，从系统动能刚度角度出发，通过分析动能变化率的大小，对研究机电液系统的节能控制、功率匹配、状态监测与故障诊断等具有重要意义。

结合机械信号调制技术，融合机电液各子系统输出的变化量，形成基于李萨如图示化的刚度在线监测方法，通过李萨如图形特征对动能刚度进行量化，获取动能变化率的大小，以评价系统动力源与负载功率匹配性。

3 动能刚度在线图示化检测方法

3.1 基于信号调制的李萨如图信息融合

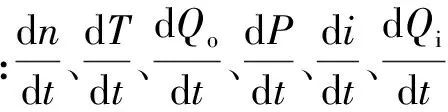
选用单位幅值的正弦信号对上述信号进行调幅处理，则可得调幅信号为

(23)

式中:A∈{n，Qo};B∈{T，P};C∈{i，Qi}。令φ=ψA-ψB，φ为动能信号与势能信号载波的相位差，ψC=ψA。令α=ωt+ψB，则

(24)

由式(24)可得

(25)

将式(25)代入式(24)可得

(26)

由式(25)、式(26)可得

(27)

当载波信号的相位差φ=180°时，由式(27)可得

(28)

同理可得

(29)

在笛卡尔坐标平面内，由式(28)、式(29)绘制的李萨如图均为过原点的直线，分别称为逆向刚度线与正向刚度线，如图2所示，其倾角的大小描述了逆向刚度与正向刚度的大小。逆向刚度线顺时针旋转，角β增大，则逆向刚度增大，反之减小；正向刚度线逆时针旋转，角α增大，则正向刚度增大，反之减小。

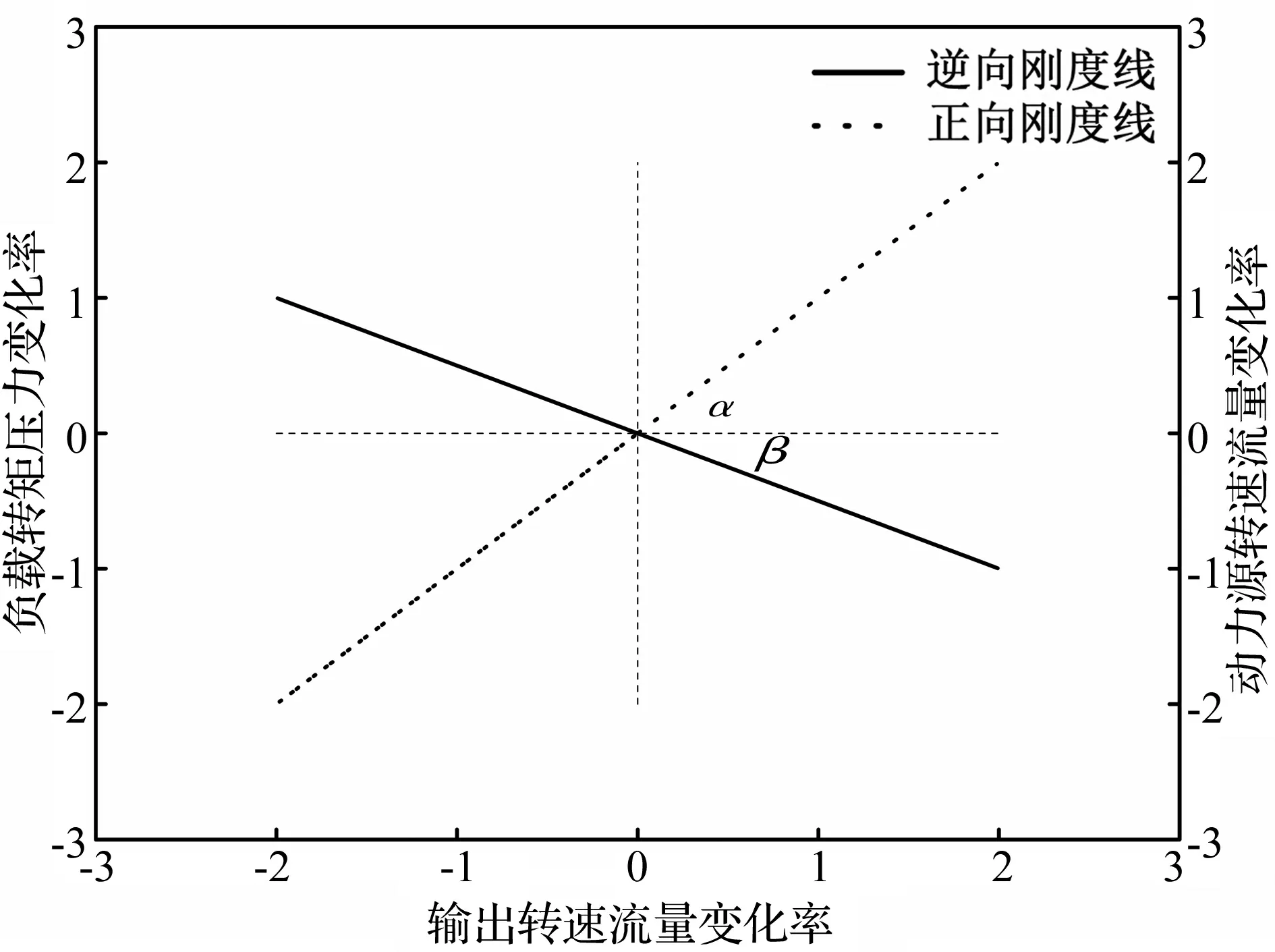
图2 动能刚度李萨如图Fig.2 Lissajous pattern of kinetic energy stiffness

3.2 动能刚度圆

机电液系统动能刚度由各子系统的动能刚度组成，设在机电液系统中，电机、液压泵及液压马达的刚度角大小分别为ζM、ζP、ζm，则可得

(30)

式中:ζM∈{αM;βM};ζP∈{αP，βP}，ζm∈{αm，βm}。

由方程组(30)在同一坐标系下绘制机电液系统动能刚度圆，如图3所示。

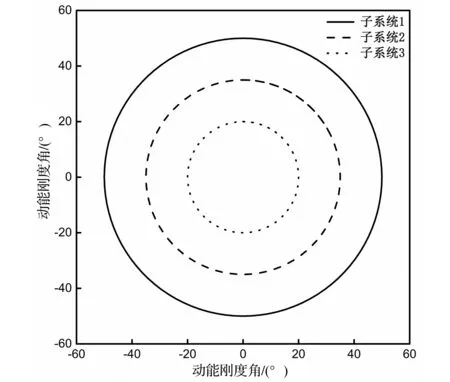
图3 机电液系统动能刚度圆Fig.3 The kinetic energy stiffness pattern for mechanical electro-hydraulic system

圆的面积代表子系统的动能刚度大小，圆环的面积代表子系统间的动能刚度损失。圆面积越大，则所代表的子系统动能刚度越大，动能变化率越小，该子系统节能效果越好。圆环面积越小，则动能刚度损失越小，子系统间的连接越趋近于刚性，能量传递过程中因动能变化率改变而产生的损失越小，系统动力源与负载之间的匹配性越好。电机拖动液压系统运行过程中，各子系统刚度圆的面积随系统负载及工况动态变化，通过动能刚度圆可实时在线检测各子系统之间的动能刚度关系与功率匹配规律。

4 机电液系统动能刚度检测实验

4.1 变转速机电液系统测控平台

如图4所示，变转速机电液系统测控平台由变转速液压系统与工控机测控系统两部分组成[13-14]。

油液经滤油器15、截止阀2-2，由永磁同步电机驱动定量泵建立系统压力，压力油流经单向阀11，通过三位四通电磁换向阀9控制柱塞马达换向，驱动柱塞马达带载工作。

液压系统的流量控制，通过变频电机驱动齿轮泵实现。伺服控制器18控制变频电机13的转速变化，从而使液压泵的输出流量改变，流量的大小与伺服控制器的输入电压大小成正比。通过控制输入磁粉制动器6的电流，使马达输出轴上的摩擦力矩变化，模拟负载工况，实现对液压系统的变载控制。模拟负载的大小与磁粉制动器的输入电流大小成正比。

如图5所示，系统运行后，伺服控制器可输出同步电机状态量——输出转矩、转速的实时监测信号；组合传感器10测量液压泵的输出压力、流量；通过磁电式转速传感器获取柱塞马达的输出转速，输出转矩经系统压力以及柱塞马达参数间接测量得到。多传感器的输出信号经数据采集卡A/D转换后，传至工控机，在开发的测控系统人机界面进行信号调制与融合，并提取图形特征，以实现机电液系统动能刚度的在线检测。

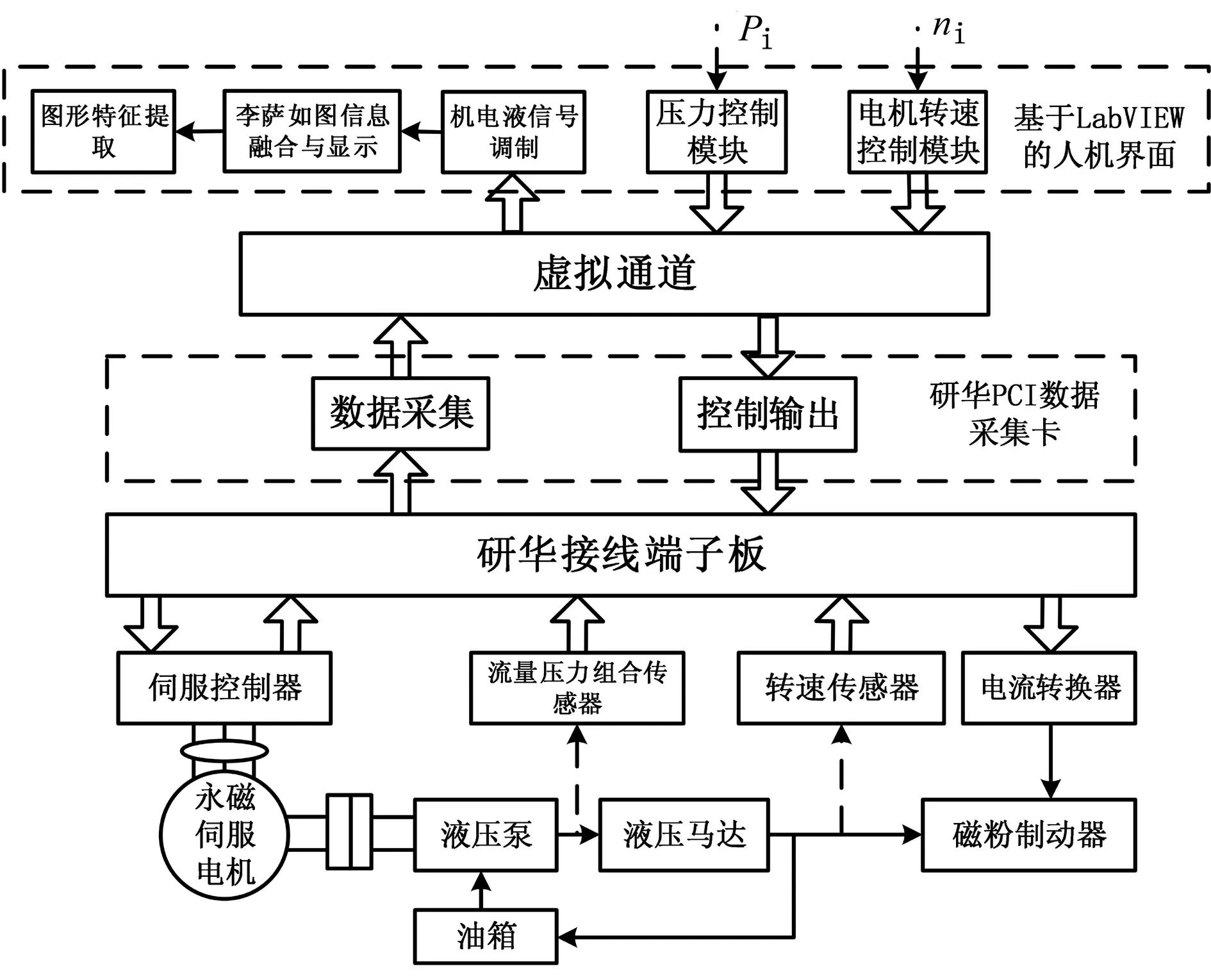
图5 基于LabVIEW的计算机测控系统框图Fig.5 The block diagram of computer measurement and control system based on LabVIEW

4.2 变载荷工况

变载荷工况时，动力源输入恒定，系统动能刚度主要受逆向刚度的影响。设定电机转速为820 r/min，控制输入磁粉制动器的输入电流，使马达输出轴上的摩擦力矩斜坡变化，模拟实际变载工况，系统压力由3.34～11.29～3.34 MPa斜坡变化。为消除量纲不同对于流量刚度与转速刚度对比的影响，选取系统空载时的转速、转矩、压力及流量作为基准进行去量纲化处理，可得机电液子系统动能刚度李萨如图的变化过程，如图6所示，动能刚度角的变化曲线如图7所示。

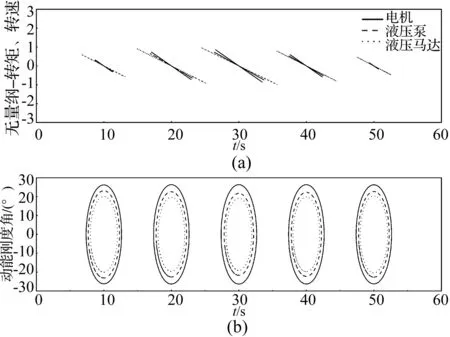
图6 变载工况机电液系统动能刚度李萨如图变化过程Fig 6.Lissajous pattern changing process of kinetic energy stiffness for mechanical electro-hydraulic system under variable load

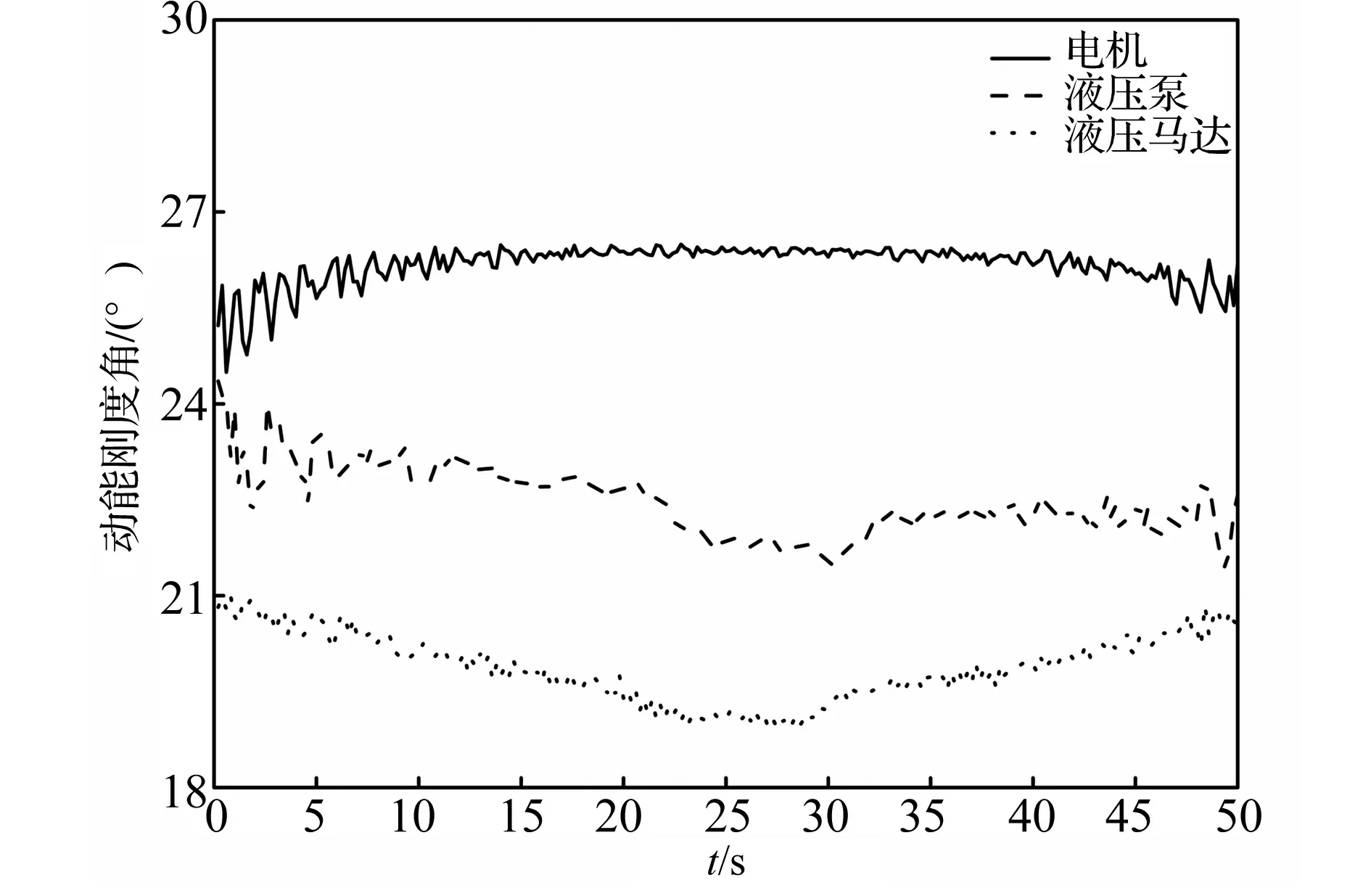
图7 变载工况机电液系统动能刚度角变化曲线Fig.7 The changing curve of kinetic energy stiffness for mechanical electro-hydraulic system under variable load

变载工况下，负载变化所产生的影响，由液压马达端至动力源端逆向传递，因此，如图6、图7所示，各子系统动能刚度逆向依次递增。由于同步电机经伺服控制器闭环控制转速，负载的变化不会引起电机转速刚度角产生较大变化，其均值为26.17°。当系统压力由3.34 MPa增大至10.29 MPa时，因油液的体积弹性模量变化较小[15]，负载压力增大主要导致泵与马达的泄漏量增大，由式(19)、式(21)可知，泵的流量刚度角由23.32°减小至21.68°，马达的转速刚度角由20.79°减小至19.03°。如图6动能刚度圆所示，电机与液压马达之间的动能刚度圆环面积增大，系统动能变化率变大，能量损失增大，节能效果变差。

4.3 变动力源转速工况

变油泵转速工况时，负载恒定，系统动能刚度主要受正向刚度影响。控制伺服控制器的输入电压，使电机转速由210～1 560～210 r/min呈斜坡函数规律变化，磁粉制动器的输入电流为0。可得机电液系统各阶动能刚度李萨如图的变化过程，如图7所示，动能刚度角的变化曲线如图8所示。

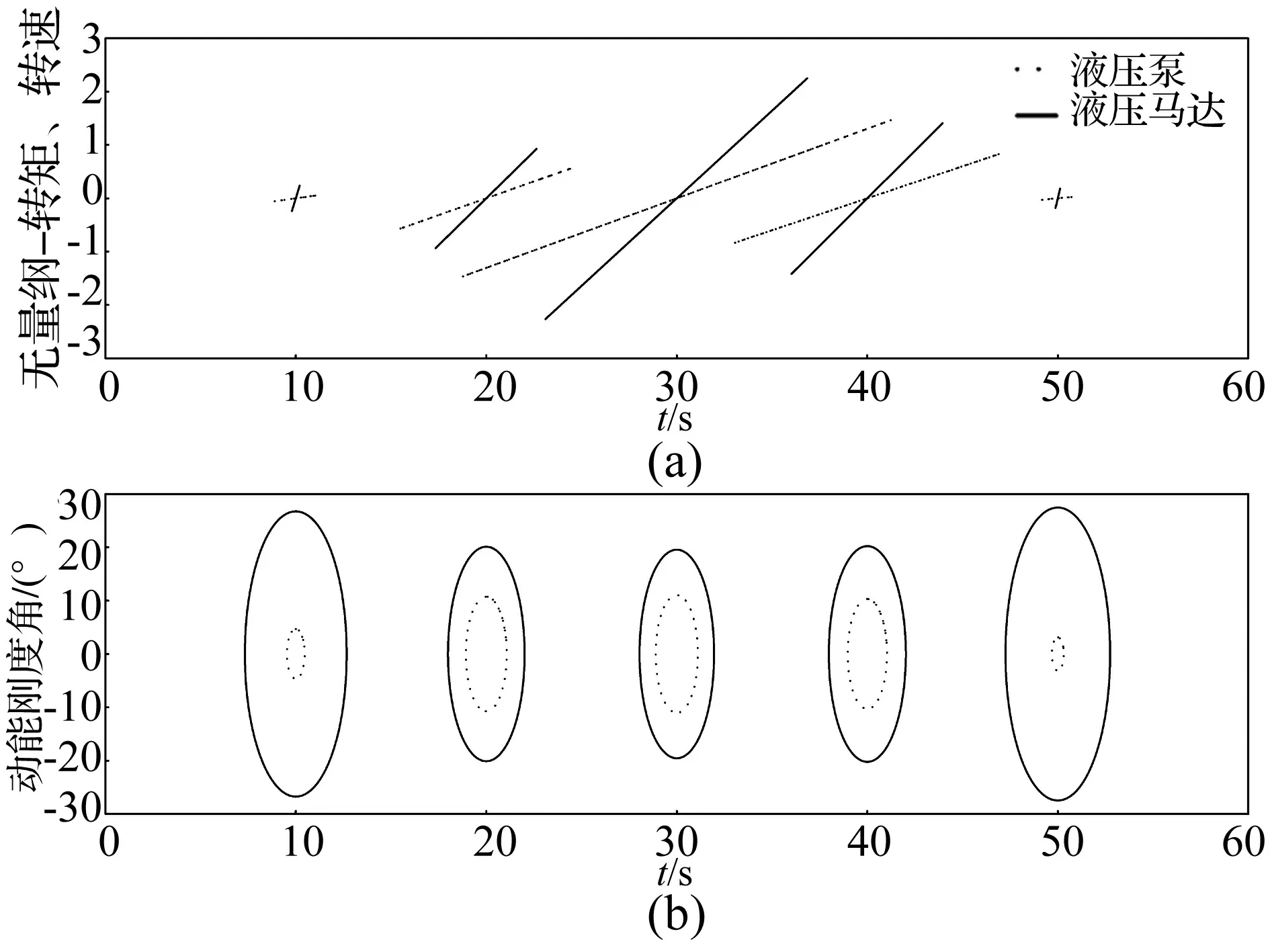
图8 变转速工况机电液系统动能刚度李萨如图变化过程Fig.8 Lissajous pattern changing process of kinetic energy stiffness for mechanical electro-hydraulic system under variable speed

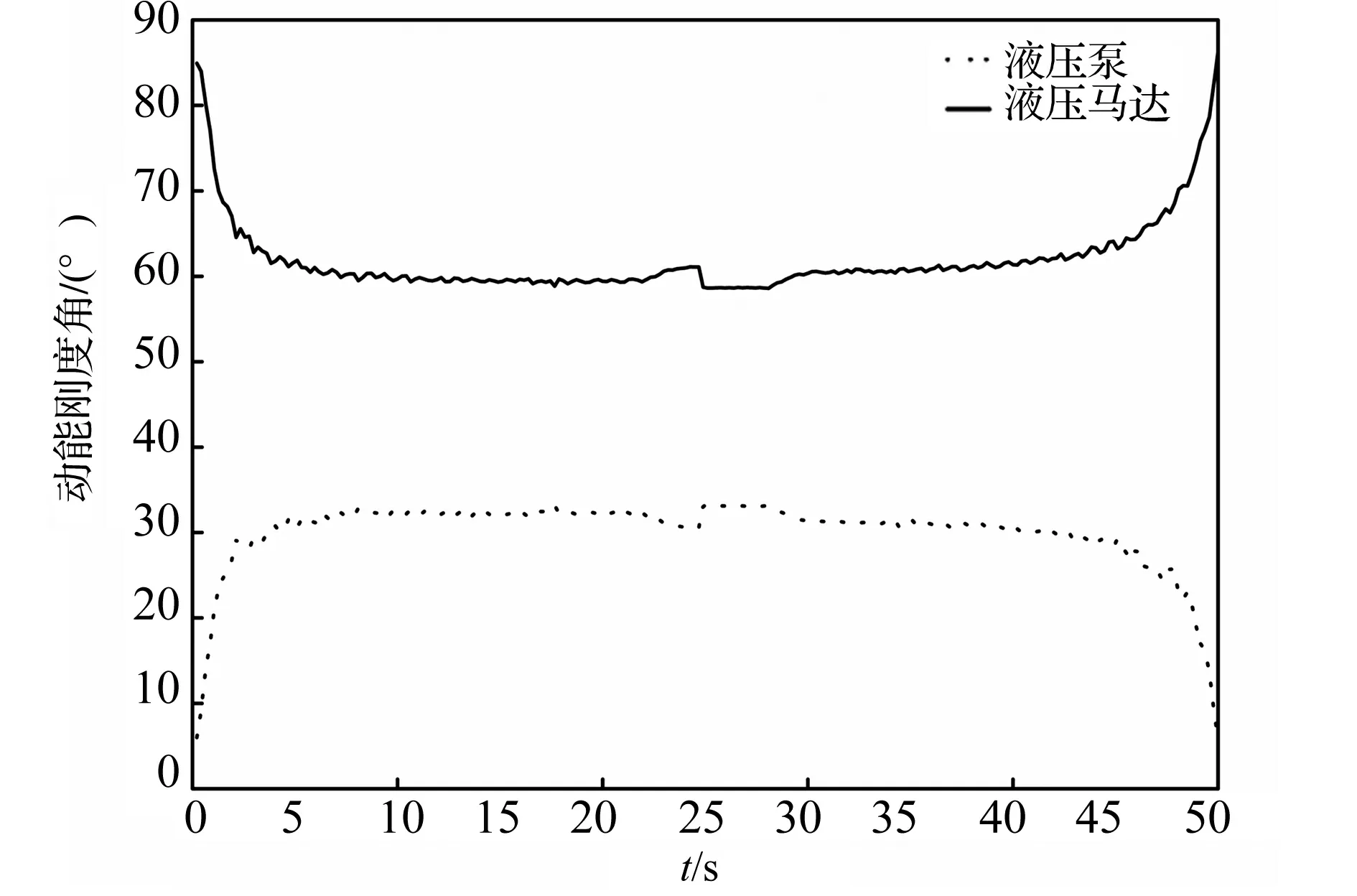
图9 变转速工况机电液系统动能刚度角变化曲线Fig.9 The changing curve of kinetic energy stiffness for mechanical electro-hydraulic system under variable speed

变转速工况时，电机转速变化所产生的影响，由动力源至液压马达端正向传递，因此如图8、图9所示，各子系统动能刚度正向依次递增。随着电机转速由210～1 560 r/min逐渐升高时，液压泵和马达的容积效率升高，油液迅速压缩，由式(19)、式(21)可知，泵的流量刚度角由6.1°迅速升高至28.13°，马达的动能转速刚度由84.93°迅速降低至64.69°，当电机转速进一步升高时，黏性阻尼及机械阻尼逐渐增大，导致系统压力逐渐升高，液压系统泄漏增大，泵和马达的动能刚度角变化变缓。当转速降低时，动能刚度角的变化相反。如图8动能刚度圆所示，圆环面积随转速的升高逐渐减小，说明低转速时，液压系统动能变化率较大，能量损失大，难以驱动液压马达带载工作，随着转速的升高，子系统间的刚度损失减小，能量传递过程中的因动能变化率而引起的损失减小，节能效果提高。

5 结 论

(1) 机电液系统动能刚度可分为逆向刚度和正向刚度两部分，逆向刚度描述系统动能抵抗负载扰动的能力，正向刚度描述系统动能抵抗动力源输出变化的能力。动能刚度越大，则系统动能变化率越小，节能效果与功率匹配性越好。

(2) 通过信号调制与信息融合技术，构建了基于李萨如图的机电液系统动能刚度图示化识别方法。李萨如图的倾角表征系统动能刚度的大小与变化规律，为客观衡量动能变化率大小，评价动力源与负载功率动态匹配特性提供了有效的方法。

(3) 根据本方法形成的李萨如图，将系统动能刚度进行量化，为对比节能控制策略的优劣，开发新型控制算法提供了技术支持。

(4) 动能刚度是机电液系统多参数耦合的结果。李萨如图倾角还包含能够反映机械惯性负载、液压系统泄漏、油液黏性阻尼以及体积弹性模量等参数的信息，仍需进一步进行挖掘。

[ 1 ] 杨世平,余浩,刘金刚,等.液压挖掘机动力系统功率匹配及其节能控制[J].机械工程学报,2014,50(5):152-160. YANG Shiping, YU Hao, LIU Jingang, et al. Research on power matching and energy saving control of power system in hydraulic excavator[J]. Journal of Mechanical Engineering, 2014, 50(5):152-160.

[ 2 ] 彭天好,杨华勇,傅新.液压挖掘机全局功率匹配与协调控制[J].机械工程学报,2001,37(11):50-53. PENG Tianhao, YANG Huayong, FU Xin. Hydraulic excavator overall power match harmony control[J]. Journal of Mechanical Engineering, 2001, 37(11):50-53.

[ 3 ] ZENG Xiaohua, YANG Nannan, PENG Yujun, et al. Research on energy saving control strategy of parallel hybrid loader[J]. Automation in Construction, 2014,38: 100-108.

[ 4 ] 车胜创.机械设计节能基本原理的分析与应用[J].长安大学学报(自然科学版),2011,31(3):95-101. CHE Shengchuang. Analysis and application of energy saving principle in mechanical products design[J]. Journal of Chang’an University(Natural Science Edition), 2011,31(3):95-101.

[ 5 ] MEUSER M, VOLLMER F. Using piezo actuators to improve the load stiffness of servo hydraulic drives[J]. Hydraulic and Pneumatic, 2003,47(10): 1-6.

[ 6 ] BAI Yanhong, QUAN Long. New method to improve dynamic stiffness of electro-hydraulic servo systems[J]. Chinese Journal of Mechanical Engineering, 2013, 26(5): 997-1005.

[ 7 ] 陈刚,柴毅,丁宝苍,等.电液位置伺服系统的多滑模神经网络控制[J].控制与决策,2009,24(2):221-225. CHEN Gang, CHAI Yi, DING Baocang, et al. Multiple sliding mode neural network control of electro-hydraulic position servo system[J]. Control and Decision, 2009, 24(2):221-225.

[ 8 ] CHENG Yichen, LI Qiangliu. Fuzzy controller design for synchronous motion in a dual-cylinder electro hydraulic system[J]. Control Engineering Practice, 2008, 16(6): 658-673.

[ 9 ] WINNICKI A, OLSZEWSKI M. Sliding mode control of electro-hydraulic servo system[J]. Measurement Automation and Monitoring, 2009, 55(3): 174-177.

[10] KARPENKO M,SEPEHRI N. On quantitative feedback design for robust position control of hydraulic actuators[J]. Control Engineering Practice, 2010, 18(3): 289-299.

[11] 谷立臣,刘沛津,陈江城.基于电参量信息融合的液压系统状态识别技术[J].机械工程学报, 2011, 47(24): 141-150. GU Lichen, LIU Peijin, CHEN Jiangcheng. State recognition technique of hydraulic system based on electrical parameters information fusion[J]. Journal of Mechanical Engineering, 2011, 47(24):141-150.

[12] 田铭兴,励庆孚,王曙鸿.交流电机坐标变换理论的研究[J].西安交通大学学报,2002,36(6):568-571. TIAN Mingxing, LI Qingfu, WANG Shuhong. Research of the reference-frame transformation theory of AC machine[J]. Journal of Xi’an Jiaotong University, 2002, 36(6):568-571.

[13] 贾永峰,谷立臣.永磁同步电机驱动的液压动力系统设计与实验分析[J].中国机械工程,2012,23(3):286-290. JIA Yongfeng, GU Lichen. System design and experimental analysis for hydraulic power unit with permanent magnet synchronous motor drive[J]. China Mechanical Engineering, 2012, 23(3):286-290.

[14] 孙昱,谷立臣,陈江城.液压动力系统电液参数耦合机理研究[J].机械科学与技术,2012,31(10):1706-1710. SUN Yu, GU Lichen, CHEN Jiangcheng. Research on the coupling mechanism of electro-hydraulic parameters for hydraulic power system[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(10):1706-1710.

[15] KIM S, MURRENHOFF H. Measurement of effective bulk modulus for hydraulic oil at low pressure[J]. Journal of Fluids Engineering, 2012, 134(2): 021201.

A graphical technique of kinetic energy stiffness identification for mechanical electro-hydraulic system

YANGBin1,GULichen1,2,LIUYong1,3

(1. State Engineering Laboratory of Highway Maintenance Equipment,Chang’an University, Xi’an 710064, China; 2. School of Mechanical and Electronic Engineering, Xi’an University of Architecture and Technology, Xi’an 710054, China; 3.School of Mechanical Engineering, Hubei University of Automotive Industries, Shiyan 442002, China)

In order to measure the kinetic energy stiffness and evaluate the power matching nature between the power source and the load, a graphical recognition method of dynamic stiffness was put forward based on information fusion using Lissajous pattern. Based on the analysis result of system modeling, the energy-saving principle of the system, physical significance of kinetic energy stiffness and its influence mechanism for the mechanical electro-hydraulic system were analyzed. By using the signal modulation and information fusion technology, the signal of torque, speed, press and flow were fused as Lissajous pattern, and the change of graphic feature could identify the dynamic stiffness on line. The results show that the change of kinetic energy stiffness is the result of intercoupling between mechanical electro-hydraulic parameters, which can be used to measure the changing rate of kinetic energy and evaluate the energy- saving effect of the system. The inclination of Lissajous pattern can characterize the kinetic energy stiffness and the value can be used to evaluate the power matching nature between the power source and the load and monitor the on-line running state.

mechanical electro-hydraulic system; kinetic stiffness; power matching; graphical recognition; information fusion

国家自然科学基金项目(51275375;51675399)

2015-11-17 修改稿收到日期：2016-02-02

杨彬 男，硕士生，1992年生

谷立臣 男，博士，博士生导师，1956年生

TH137

A

10.13465/j.cnki.jvs.2017.04.019