非线性铁木辛柯梁饱和吸振

杨 柳， 杨绍普， 杨月婷

(1.北京交通大学 机械工程学院，北京 100044； 2.石家庄铁道大学 机械工程学院，石家庄 050043)

非线性铁木辛柯梁饱和吸振

杨 柳1， 杨绍普2， 杨月婷2

(1.北京交通大学 机械工程学院，北京 100044； 2.石家庄铁道大学 机械工程学院，石家庄 050043)

主要研究了利用饱和现象降低非线性梁的振动。基于哈密尔顿最小势能原理建立非线性梁的动力学模型，利用多尺度方法求解非线性梁系统的频率响应方程，通过调节有效参数使梁进入饱和状态，梁的振动得到效抑制。

非线性梁;多尺度方法;饱和吸振

在工程中柔性梁经常出现颤振和共振现象，引起梁的较大弯曲变形，对梁的结构的稳定性和疲劳寿命带来了严重影响，尤其是在高速直升机飞行中，出现的共振动现象会对直升机机翼产生大的动态变形。所以如何避免和减小柔性梁的振动成为了梁动态分析的关键。

本文将压电陶瓷应变片嵌入铁木辛柯梁中，研究其出现内共振和共振时，通过控制参数，使主系统的响应进入饱和状态，激励幅值和能量传递到振子中，从而实现梁的减振。

非线性吸振器的理论和实验已经得到广泛的关注和应用，NAYFEH等[1]研究船的非线性模型时首次提出了饱和现象吸振，并研究了多自由度柔性梁的控制实验，分析了1∶2内共振时系统饱和吸振。PAI等[2]发展了柔性结构非线性主动吸振器，并对饱和吸振进行了分析。OUEINI等[3]研究了立方非线性吸振器在线性悬臂梁动力学分析。EISSA等[4]研究了非线性摆主动控制和半主动控制。SAYED[5]分析了主动控制吸振1∶2和1∶3共振下系统振动。基于饱和吸振下，几种非线性吸振器已经展示出良好、有效的结果，其中,BANERJEE等[6]证明了霍普分叉和混沌的存在。这种饱和现象也被越来越多的领域利用，EISSA等[7]建立直升机机翼动态模型，分析了1∶3内共振下机翼颤振控制。

1 非线性控制梁的动力学模型

根据材料变形理论和扭转力影响，铁木辛柯梁的应变关系

εy=0

(1)

压电陶瓷材料的的应变

(2)

受电压作用的下的陶瓷压变本构关系

(3)

(4)

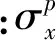
由弹性力学得

τxy=μ·γ

(5)

根据梁的变形理论，将式(1)、式(5)代入式(6)，形变分量εx，γ的形变势能U1为

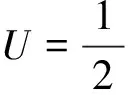
(6)

初始应变为零，梁的动能T为

(7)

式中,ρ和I为密度、截面惯性矩。梁的截面是关于z轴对称的，所以∫AzdA=0。

外力势能，包含体力、面力表示为

(8)

依据哈密尔顿原理

(9)

简化得铁木辛柯梁的控制方程

εβφ(τ)=F(x,t)+G1

(10)

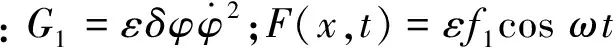
2 近似求解

多尺度法对铁木辛柯梁方程式(10)中ν(τ)和φ(τ)做一阶近似展开

v(τ,ε)≅v0(T0,T1)+εv1(T0,T1)

φ(τ,ε)≅φ0(T0,T1)+εφ1(T0,T1)

(11a)

时间尺度的时间变量Tn=εnt(n=0,1)

对式(11)中的时间变量进行微分，按ε的幂次展开

(11b)

由于0<ε<1，忽略比o(ε2)高阶项，将式(11b)代入式(10)中提取ε0及ε1项方程得

ε0项

(12)

ε1项

(13)

2ξ2ω2D0φ0+α2v0

(14)

式(12)解的形式为

(15)

式中,cc项为共轭项。

(16)

将式(15)代入式(13)～式(14)中得

(17)

α2eiω1T0+cc

(18)

系统的两个固有频率满足

ω=ω1+εσ1，ω1=ω2+εσ

(19)

消去式(17)～式(18)中的永年项得

-[2iω2(D1B+ξ2ω2B)]+α2AeiσT1=0

(20)

将式(19)代入式(23)中分离虚实部得

(21)

(22)

(23)

(24)

式中:θ1=σ1T1-κ1;θ2=κ1-κ2+σT1。

方程的一次近似解为

v=a(T1)cos[ω1T0+σ1T1-θ1]

φ=b(T1)cos[ω1T0-θ1-θ2]

3 1∶1内共振条件下的定常解

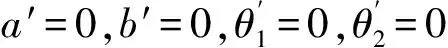
(25)

(26)

(27)

(28)

单振子解当b=0,a≠0时，方程的频幅解为

(29)

双振子解当b≠0,a≠0时，方程的频幅解为

(30)

4 非线性定常解的稳定性

对方程加扰动量，a=Δa+a0，b=Δb+b0代入式(21)～式(24)得

(31)

(32)

(33)

(34)

非线性微分方程的特征值矩阵为

(35)

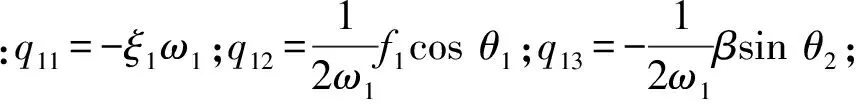
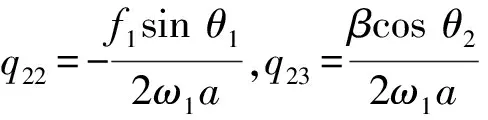
其中,

λ4+c1λ3+r2λ2+r3λ+r4=0

(36)

根据Routh定理判定系统稳定区域，λ为负值时系数应满足

c1>0,c1c2-c3>0,c4>0,

5 数值分析

5.1 幅频响应

给定f1=4,ξ1=0.03,ξ2=0.006,。ω≈ω1且内共振时不同参数作用下，幅频响应。如图1所示，给出有无饱和吸振下对比。如图2～图5所示，在饱和吸振中，不同参数对系统的影响。

如图1所示,对比有无饱和控制下梁的幅频曲线影响。当α1=0,α2=0，出现内共振时，系统无饱和吸振，响应幅值较大。当α1≠0,α2≠0时，调节激励频率大小，使系统进入饱和状态，幅值得到有效降低。

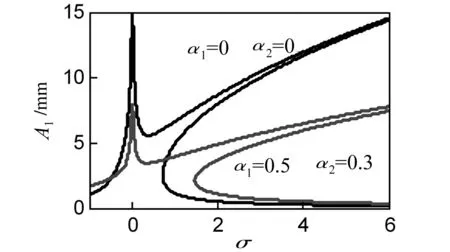
图1 控制参数的影响Fig.1 Control parameter

由图2可知，不同阻尼系数ξ1作用下，随着ξ1的增加，梁的右端幅值程减小趋势，对系统幅值大小影响较大。

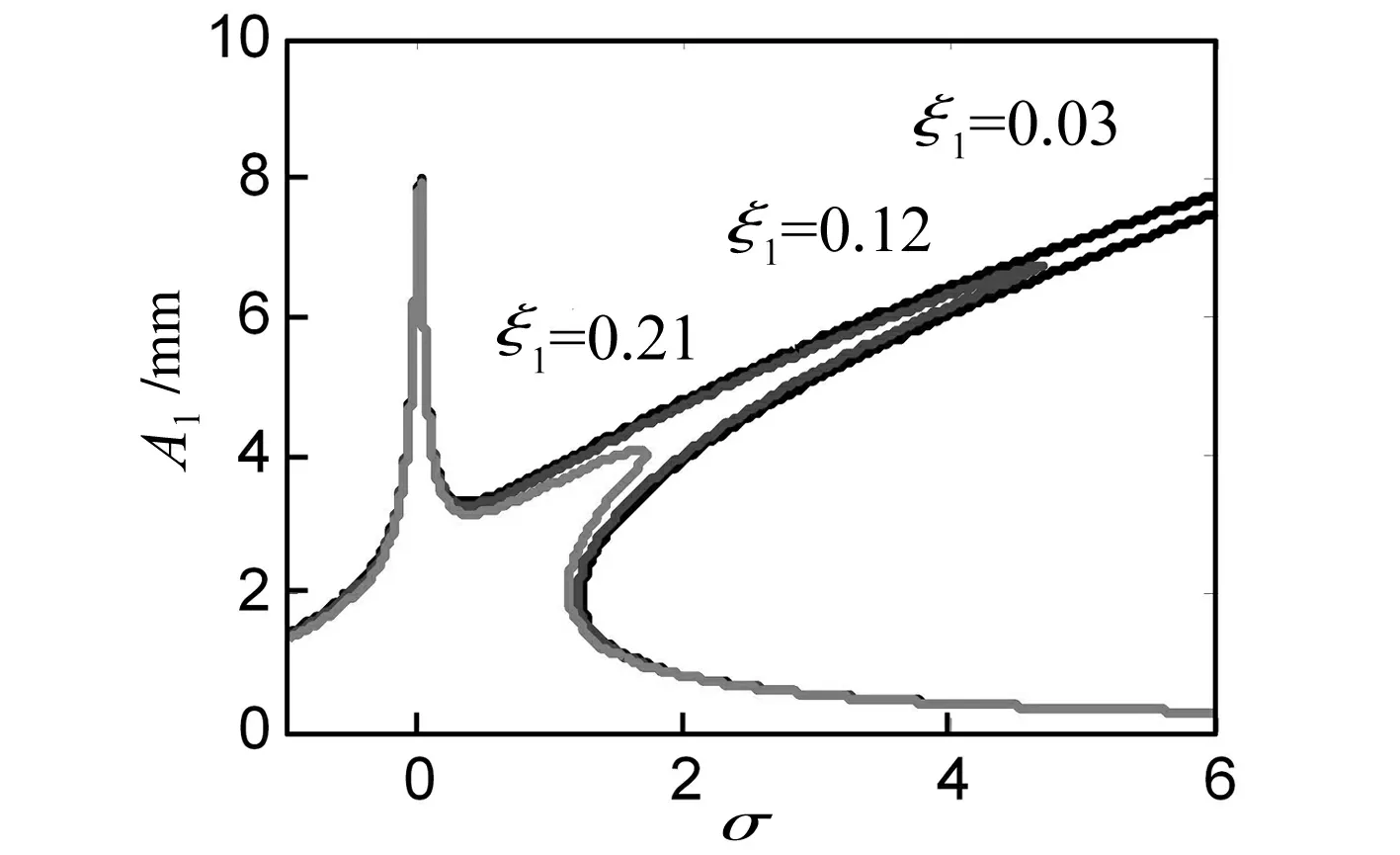
图2 阻尼参数ξ1的影响Fig.2 Damping parameter ξ1

由图3可知，不同频率系数ω1作用下梁的幅频曲线。随着ω1的增加，梁的右端幅值程减小趋势，对系统幅值大小及稳定域影响较大。

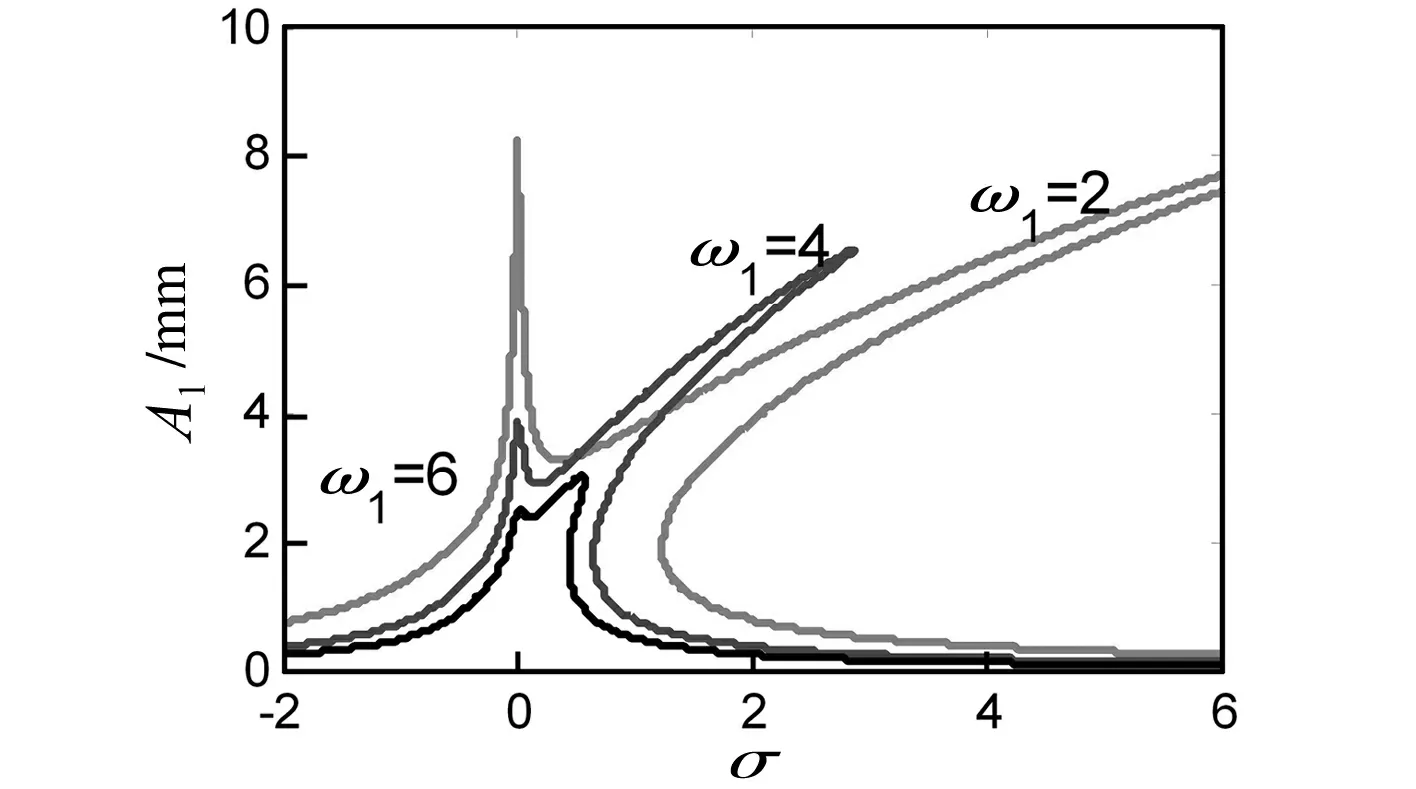
图3 频率ω1的影响 Fig.3 Frequency parameter ω1

如图4所示,不同系数α1作用下梁的幅频曲线。随着α1的增加，梁的右端幅值增小。右端幅值像右偏，定常解的稳定区域变大。

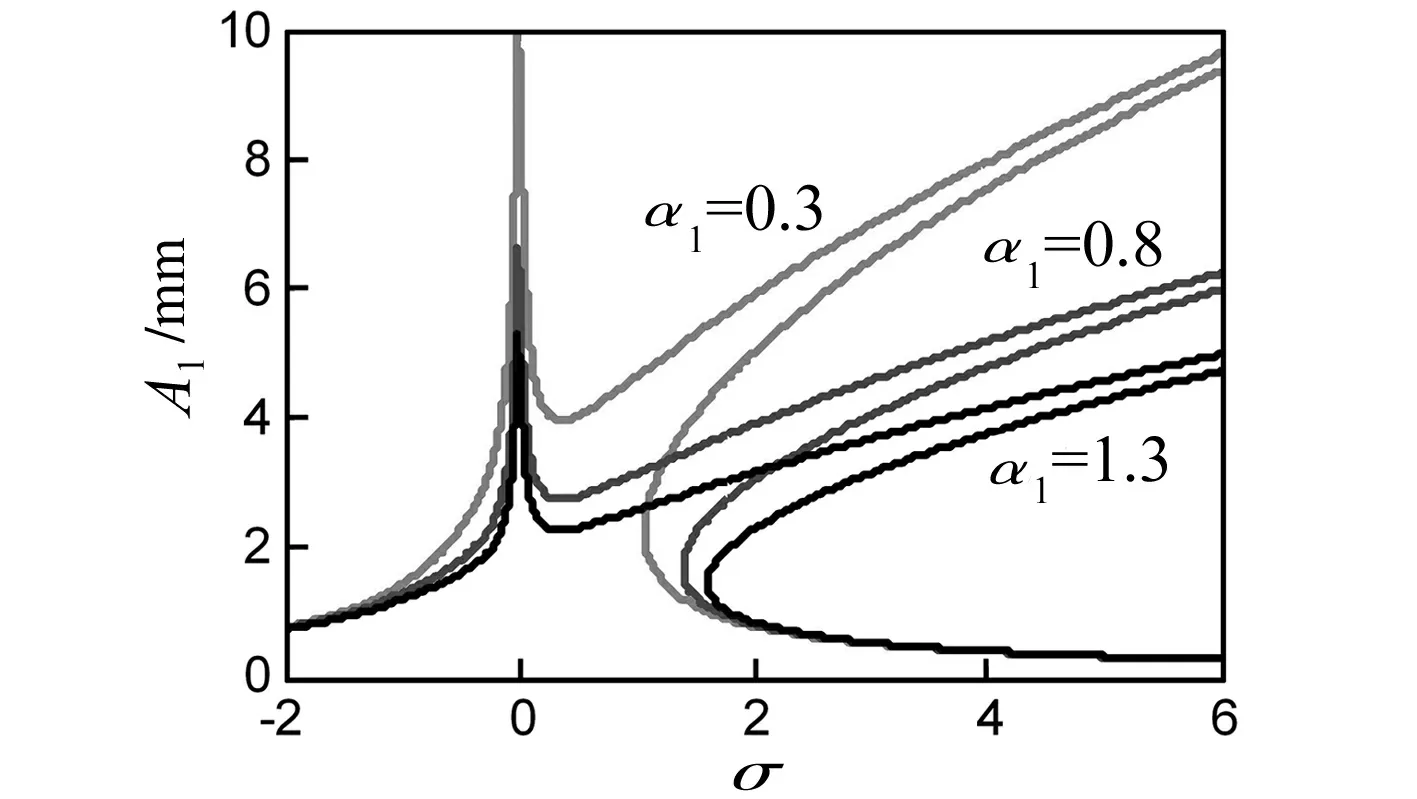
图4 参数α1的影响Fig.4 Parameter α1

5.2 激振力响应曲线

内共振时，如图5所示，对比有无饱和吸振下激励与响应的变化。如图6～图9所示，选取不同参数，使系统进入饱吸状态时，分析激振力与挠度变化。

由图5可知，无饱和控制下梁的幅频曲线影响。当α1=0,α2=0，出现内共振时系统无饱和吸振，响应幅值随f1增大。当α1≠0,a2≠0时，系统进入饱和状态，幅值随f1增大缓慢上升，饱和吸振下使系统幅值得到有效抑制。

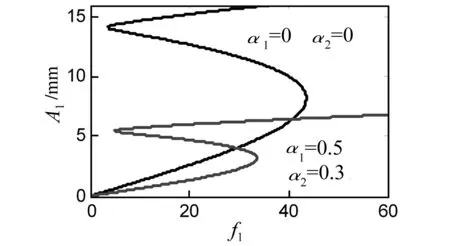
图5 控制参数的影响Fig.5 Control parameter

如图6所示，线性阻尼系数ξ1的增加，挠度值下降，稳定区域增加。幅值存在多解，阻尼值到达一定值，幅值曲线平缓上升，激振力影响减弱。

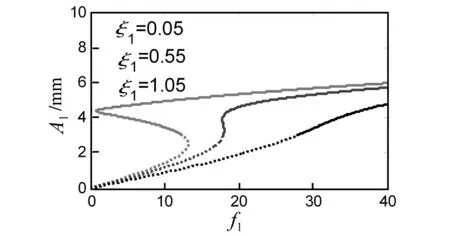
图6 阻尼参数ξ1的影响 Fig.6 Damping parameter ξ1

如图7所示，非线性立方项α1的增加，挠度值下降，稳定区域增加。幅值存在多解，当系数α1达到阈值时，系统幅值进入饱和状态。

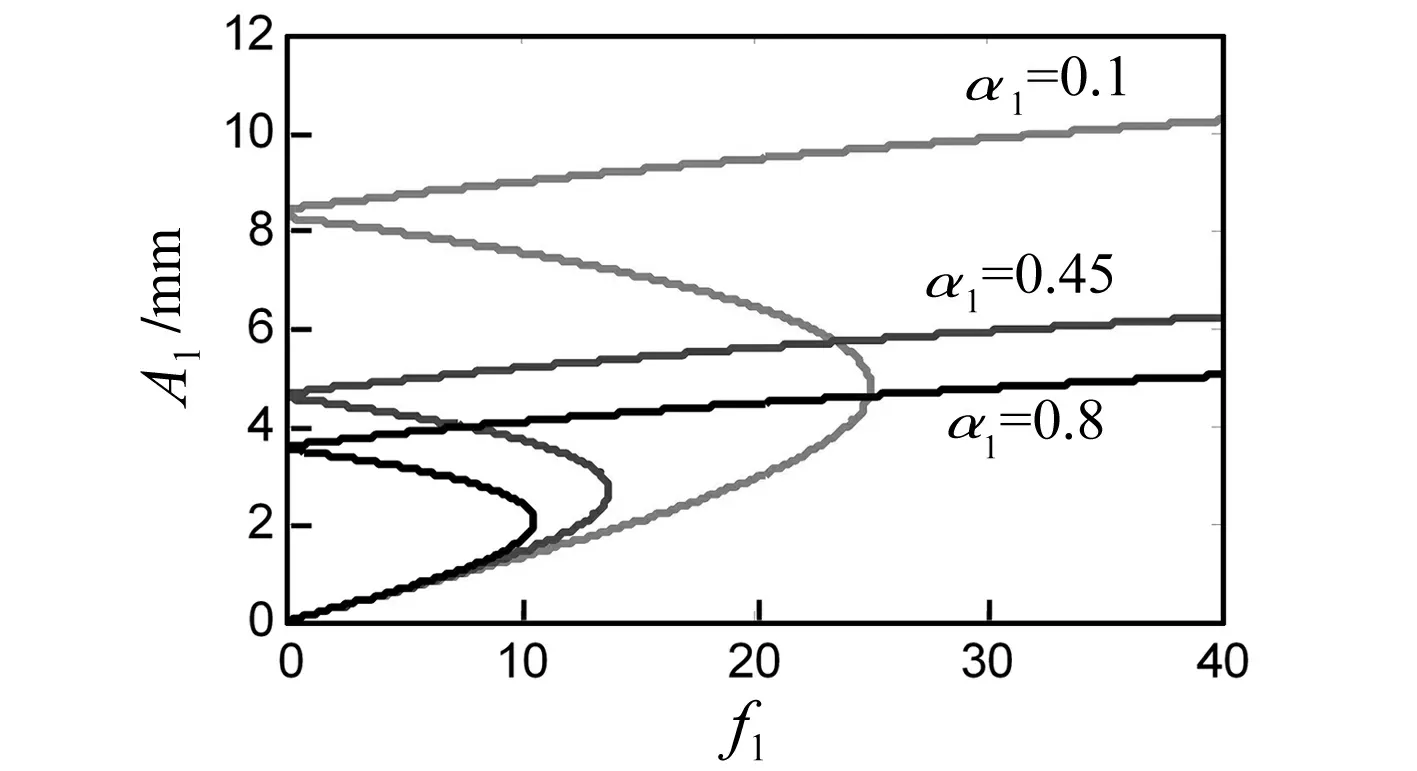
图7 参数α1的影响Fig.7 Parameter α1

如图8所示，频率系数ω1的增加，挠度幅值增大，稳定区域增加。幅值存在多值解区域增大。

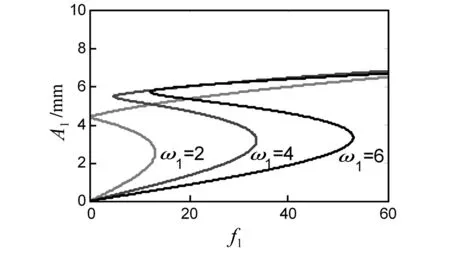
图8 参数ω1的影响Fig.8 Parameter ω1

如图9所示，σ的增加，挠度值下降，稳定区域增加。幅值存在多解区域增加，控制系数到达一定值，幅值曲线平缓变化。

5.3 时域响应

当α1=0,α2=0时，不出现饱和状态时系统的时域图(见图10)。

当α1≠0,α2≠0时，饱和现象时系统的时域图(见图11)，梁的稳定响应幅值降低至无饱和状态梁稳定响应幅值的5%，突出显示发生内共振时控制系统出现饱和吸振很好改善了梁的振动。

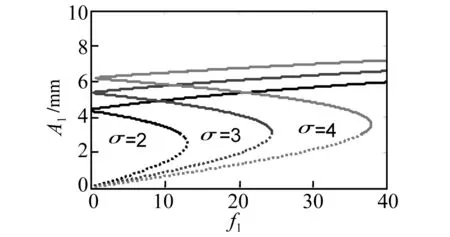
图9 参数σ的影响Fig.9 Parameter σ

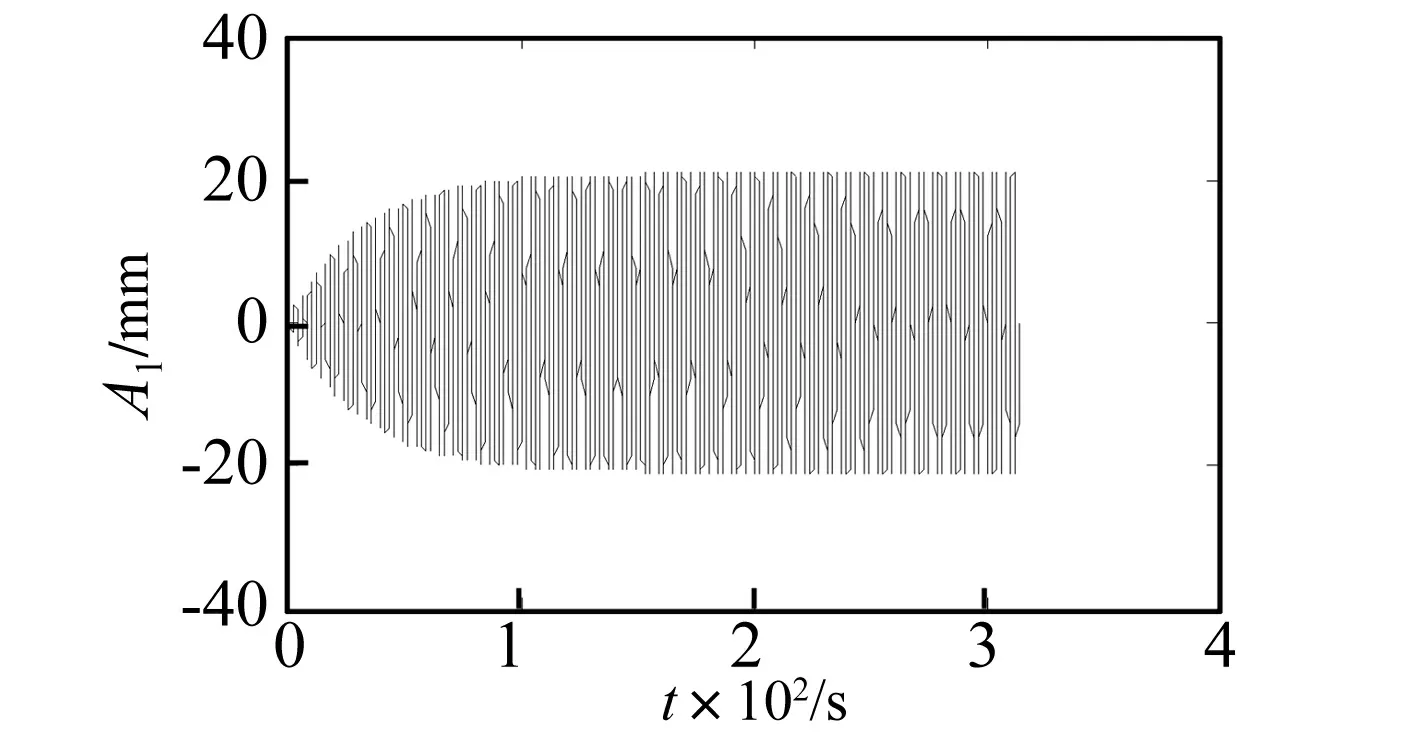
图10 位移时间历程Fig.10 The displacement-time history

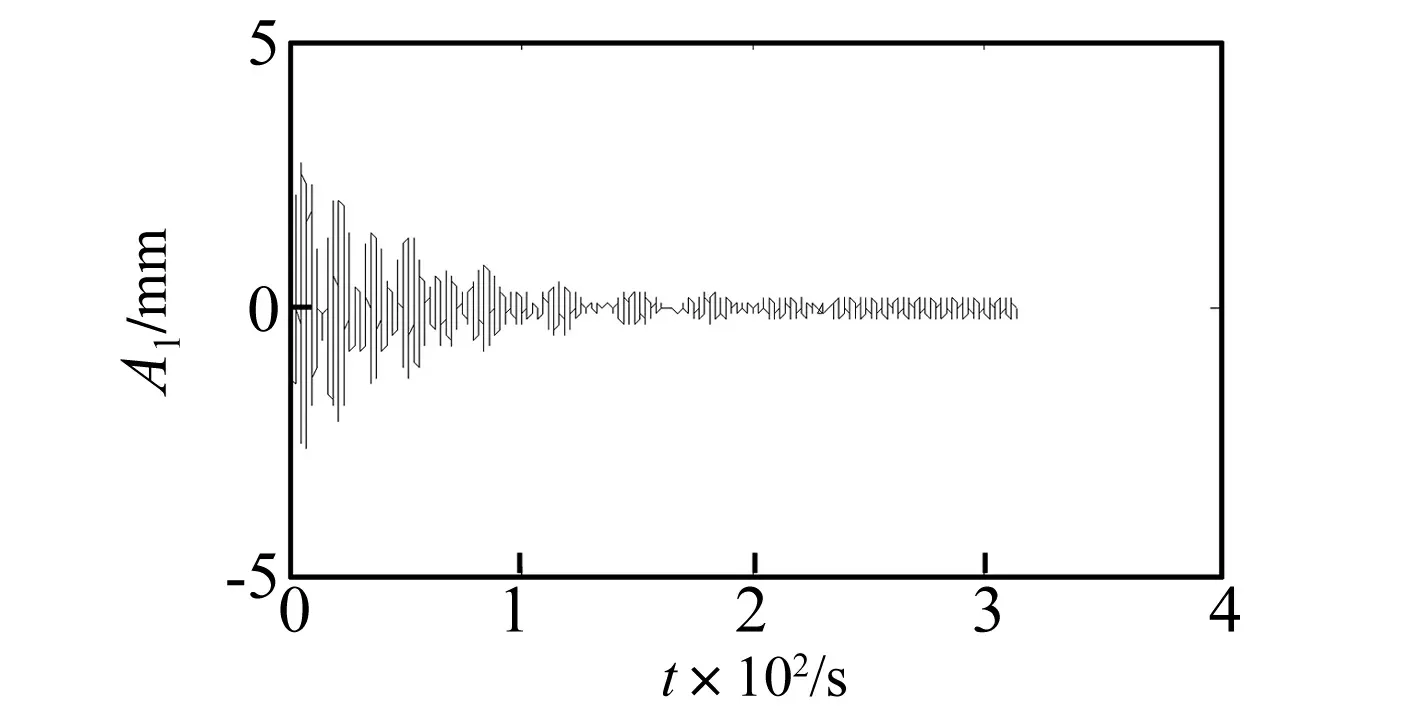
图11 位移时间历程Fig.11 The displacement-time history

6 结 论

建立了嵌入陶瓷压电结构柔性梁的动态模型，近似求解，分析了稳定域。系统出现饱和现象能够有效地抑制梁的主共振及内共振幅值。

饱和吸振具有更好的减振效果及反应时间更短，通过控制和调整系统参数能够使得振动得到有效抑制。

航空航天更多使用复合材料，饱和吸振被广泛的应用和研究。

[ 1 ] NAYFEH A H, MOOK D T, MARSHALL L R. Nonlinear coupling of pitch and roll modes in ship motion[J]. Journal of Hydronautics, 1973, 7(4):145-152.

[ 2 ] PAI P F,WEN B, NASER A S, et al. Structural vibration control using PZT patches and nonlinear phenomena[J]. Sound Vibration, 1998, 215(2): 273-296.

[ 3 ] OUEINI S S, NAYFEH A H. Analysis and application of a non-linear vibration absorber[J]. Vibration Control and Shock, 2000,6(7):999-1016.

[ 4 ] EISSA M, SAYED M. Vibration reduction of a three DOF non-linear spring pendulum[J]. Commun Nonlinear, 2008, 13(2):465-488.

[ 5 ] SAYED M. Improving the mathematical solutions of nonlinear differential equations using different control methods[D].Egypt:Menofia University,2006.

[ 6 ] BANERJEE B, BAJAJ A K, DAVIES P. Second order averaging study of an autoparametric system[C]//New York:In Nonlinear Vibrations ASME, 1993:127-138.

[ 7 ] EISSA M, EL-SERAFI S, ABD-EL-MONIEM R. Vibration reduction via 1∶2 internal resonance active absorber[J]. Scientific Bull Factor, English Ain-shams University,2006, 41(3):971-986.

Nonlinear Timoshenko beam saturated absorber

YANGLiu1，YANGShaopu2,YANGYueting2

(1.School of Mechanical Engineering, Beijing Jiaotong University, Beijing 100044, China; 2.School of Mechanical Engineering, Shijiazhang Railuay University, Shijiazhang 050043, China)

The objective of this study was to reduce vibration by the saturation control. Nonlinear beam dynamic model was established by using Hamilton’s principle of minimum potential energy principle. The frequency responding equation of nonlinear beam was solved with the multi-scale method. The nonlinear beam was saturated by adjusting the effective parameters. The vibration of the nonlinear beam was thus suppressed effectively.

nonlinear beam; multiple scales method; saturation

国家自然科学基金(11227201)

2015-11-13 修改稿收到日期：2016-01-31

杨柳 男，博士生，1987年生

杨绍普 男，教授，1962年生

O322

A

10.13465/j.cnki.jvs.2017.04.008