冷却塔风振响应时程计算和风振系数分析

张军锋， 葛耀君， 赵 林

(1. 郑州大学 土木工程学院，郑州 450001； 2. 同济大学 土木工程防灾国家重点实验室，上海 200092)

冷却塔风振响应时程计算和风振系数分析

张军锋1, 2， 葛耀君2， 赵 林2

(1. 郑州大学 土木工程学院，郑州 450001； 2. 同济大学 土木工程防灾国家重点实验室，上海 200092)

为全面获得冷却塔塔筒的风致动力响应特征，探究各响应包括内力和位移的峰值因子g、动力放大系数D以及用于结构设计的风振系数β的取值和各参数在不同响应间的差异，以某大型冷却塔为例，经风洞试验获得塔筒表面风压时程，采用时程方法进行结构动力响应计算。分析表明，作为空间结构，不同位置不同响应的g值和D值有较大差异，难以直接应用；但结合各响应的时程特征、塔筒结构特性及配筋设计原则，可以将塔筒的g值和D值从环向和子午向的二维分布简化为仅沿子午向的一维分布，由此所得各响应的D值可达工程实用范围，但用法与现行设计方法仍不一致；根据环向和子午向配筋设计的独立性，并考虑风致各内力在结构设计中的不同权重，在实用中对D值可仅区分环向内力和子午向内力独立取值，但环向内力的D值要大于子午向内力。此时，环向和子午向的D值即可作为风振系数β参与结构设计。

冷却塔；风洞试验；时程分析；峰值因子；动力放大系数；风振系数

众所周知，风荷载是冷却塔的设计控制荷载，风荷载的动力作用作为冷却塔结构研究的关键问题之一，长期以来一直受到设计和研究人员的关注[1-2]。尽管国内外学者通过风洞试验和数值计算积累了大量例证，但各国冷却塔设计规范对风荷载动力作用的分析理念、计算方法、应用形式以及具体结果等都仍有较大差异[3]，这也说明对此问题仍没有明确和统一的认识。随着冷却塔高度的持续增加且壁厚相对更薄，结构愈加轻柔，对风荷载的动力作用将更加敏感，亟需明确冷却塔的风致动力响应特征及实际应用方式。

气弹模型风洞试验可以直接得到结构的风振响应，但无论是连续介质[4-8]和等效梁格模型[9-11]都只能分别获得有限测点的轴力和位移，无法同时获知整个塔筒的所有响应及特征，包括环向弯矩这一关键内力。这也使冷却塔的风振响应和等效风荷载分析常以单个响应的风振效应，如子午向轴力或塔筒位移，代表整个塔筒所有响应的风振效应。但不同内力与位移的风振效应是不同的[12-13]，单个响应的动力放大系数D并不能直接应用于其他响应。即使根据计算获得所有响应的风振效应，如何对结果进行分析以获得用于结构设计的风振系数β仍缺乏统一认识。

冷却塔风致响应计算有频域[10-14]和时域[14-20]两种手段，但频域所得结果只是脉动响应的频谱和根方差，时程的缺失也难以建立对结构响应的直观认识[15]。同时，根据Davenport峰值因子理论，响应时程的缺失也无法明确响应的峰值因子g，故不得不采用风荷载的g值作为响应的g值[21]或者根据经验指定g值。

尽管冷却塔的时域计算有较长的历史，但因结构计算模型庞大且脉动风压数据来源有限，故算例较少，近20年所见文献仅有5篇：BARTOLI等虽给出了时程计算结果，但主要侧重于冷却塔表面随机风压场的数值模拟，并未对计算结果做必要的分析；ORLANDO在计算中认为结构的共振响应有限从而忽略了结构的共振效应；文献[18]只简单给出了内力计算结果而未详加分析；文献[19-20]仅给出了位移响应，但内力才是结构设计的关键指标。另外，上述文献对涉及的计算参数也未有系统完整的介绍，包括风洞模型风压时程向原型结构转换的缩尺比、计算时长、时间积分步长、结构频率分布、结构阻尼比以及非线性效应等，这些参数的取值合理与否直接关系计算结果的可靠性。比如文献[18-20]的计算时长仅分别有13 s、1 024个时点、204.8 s、100 s，远低于10 min时距要求[22]，可能对脉动响应结果造成误差。

以国内规划中的某内陆核电厂大型冷却塔为例，通过刚体模型风洞试验获得冷却塔表面风压时程，采用直接积分和模态叠加两种方法进行结构动力时程响应计算，全面获得各响应的风致动力响应特征。根据计算结果，对不同响应的峰值因子g和动力放大系数D取值以及不同响应间的差异进行了详细分析，并根据冷却塔的结构特性和设计原则给出了实际设计中风振系数β的取值。

1 工程背景与计算方法

本研究中的冷却塔特征尺度如图1所示，塔高已经远远超过了现行规范[23]关于风振系数的适用要求(≤165 m)。塔筒采用分段等厚，底部最大厚度1.8 m，中部最小厚度0.27 m，由46根一字柱与基础连接。原型结构处B类场地，10 m高度基本风速V0=26.7 m/s，塔顶风速VH=40 m/s。

图1 冷却塔结构及模型示意Fig.1 Geometry of the hyperboloidal cooling tower and the FEM model

风洞试验模型几何缩尺比λL=1∶200，刚体测压模型表面布置14排断面，每排断面36个测点，共14×36=504个测点。限于设备采集能力，仅测面A的9排断面同步测量并用于时程计算，测面B的5排测点仅用于对照复核。试验在同济大学TJ-3风洞中进行，模拟B类地貌，塔顶试验风速为10 m/s，即风速比λV=1∶4，由此可推算时间比为λt=1∶50。信号采样频率312.5 Hz，采样时长19.2 s，每个测点6 000个数据。塔筒表面均匀粘贴36道3层0.1 mm厚纸带并配合试验风速进行雷诺数效应模拟，图2给出了测面A断面的平均风压、脉动风压以及峰值因子g分布。图中各断面的参考风压均为本断面高度的来流速压，峰值因子g依据Davenport理论(式(1))所得。试验及结果的详细介绍可见文献[24]。

(1)

式中：S(f)为脉动风谱，v可理解为风压频谱的平均频率，T为风速统计时距并依规范取T=360 s。

图2 不同断面的环向风压参数Fig.2 Wind pressure parameters of different sections

采用ANSYS程序进行结构计算，塔筒采用Shell188单元模拟，下支柱和檐口采用Beam188单元模拟。计算耗时与有限元模型划分精度密切相关，据文献[10]，对冷却塔适当降低模型划分精度对结构振型和频率的影响可以忽略，亦不会对结构响应有明显影响。因此，为节约计算机时并多次试算，对塔筒环向和子午向各划分72和35个单元。为便于塔筒与下支柱的连接，结构初设的46根一字形下支柱按等刚度原则调整为72组人字形下支柱。结构前100阶频率分布如图3示。

图3 结构频率分布Fig.3 Frequency distribution of the HCT model

时程计算采用隐式的Newmark直接积分完全法进行。风荷载时程采用风洞试验的结果，并通过POD分解和预测，将9×36=324个风压测点扩展到36×72=2 592个有限元节点[25]。根据时间缩尺比λt=1∶50，采样频率和时长换算为原型结构分别为6.25 Hz和16 min，采样时长满足10 min时距要求。计算中，所加风荷载为包括平均和脉动分量的完整风压，故去除前375个时程点的响应以消除突风效应的影响[26]。显然，刚体模型风洞试验可以直接获得非定常气动力，时程计算又可计入多模态贡献及不同模态之间的耦合效应[22]；试验虽无法获得自激力效应，但有研究表明自激力效应在冷却塔风振响应分析中可以忽略。另外，计算表明，冷却塔在风荷载作用下的几何非线性特征极不明显，故下文计算中不予考虑。

对于时程计算中结构参与模态数量，文献[27]根据原型冷却塔动力特性测试结果以及风荷载特性分析认为，计入前30阶振型就已经可以满足计算精度；文献[10-11]的频域计算结果表明，计入前50阶模态的响应即可满足计算精度要求。下文计算同样截取50阶模态(图3)，相应的最小时间积分步长为Δt=1/(20×1.803)=1/36.1 s。为满足Δt要求，将各时程点之间内插6个子步，实际计算Δt=1/(6×6.25)=1/37.5 s。同时，为保证计算精度，还分别采用2Δt和0.5Δt的时间积分步长进行计算。结果表明，2Δt所得各高度最大响应的脉动性均有不同程度的下降，而0.5Δt所得各高度最大响应的根方差和最大值变化不超过2%，这也说明计算中所考虑的模态数量和时间步长是合理的。

模态阻尼比ξ是在结构动力响应分析中一个重要参数。在已有的冷却塔计算例证中，对ξ取值或无明确说明，或直接按混凝土结构取ξ=5%或4%，或直接据试验模型取ξ=3.5%或2.5%。但冷却塔原型结构的动力特性实测结果表明，其不同模态的ξ仅约为1%左右[27-29]。故在计算中采用瑞利阻尼对第1阶和第70阶模态设定ξ=1%，前100阶模态的ξ分布在0.8%～1.3%。

在时程分析中，每个响应均有多个特征值，如均值(Mean)、根方差(Rms)、最值(时程序列中的最大值Max或最小值Min)以及用于结构设计的包含一定保证率的极值(Extreme)等。极值的确定一般有两种方法，或是先以式(1)计算或由经验指定峰值因子g，再以式(2)计算极值；或者直接取时程的最值(Max or Min)为极值，g则由式(2)反算。各响应的动力放大系数D则由式(3)确定。下文对各响应的分析也围绕g和D这两个参数展开。

Extreme=Mean±g×Rms

(2)

D=Extreme/Mean=1±g×Rms/Mean

(3)

除采用上述直接积分法进行计算外，还采用模态叠加法进行了校核计算。模态叠加法计算中：①试验风压到原形结构风压的处置与直接积分法相同；②仅加载脉动风压，但同样去除前375个时程点的响应以便对比；③计入前100阶模态并取ξ=1%。对比表明，对于下文一维分布简化后的g和D，两种计算方法所得各响应的g和D一致性良好，误差一般不超过1%。下文所列均为直接积分法的结果。

2 计算结果及分析

冷却塔风荷载作用下的结构设计控制指标为子午向轴拉力FY,T、环向弯矩MX、塔筒上端局部区域的环向轴拉力FX,T，结构位移U也是传统关注指标，故下文也主要针对这几个响应的g和D进行分析，子午向弯矩MY的数值极小，在结构设计中可以忽略。下文对塔筒区分环向和子午向两个维度，环向角度θ以迎风点为0°，逆时针转动为正；子午向以0≤hS/HS≤1表示塔筒相对高度位置(图1)。静风响应结果在诸多文献中均有介绍，故不再专门给出。

2.1g和D的二维分布

峰值因子g是风振响应分析的一个重要参数，用以确定响应极值。但在冷却塔结构分析中对g的取值并不一致：或根据经验指定，或以时程最值作为极值， 或先以位移响应时程最值作为极值， 反算得

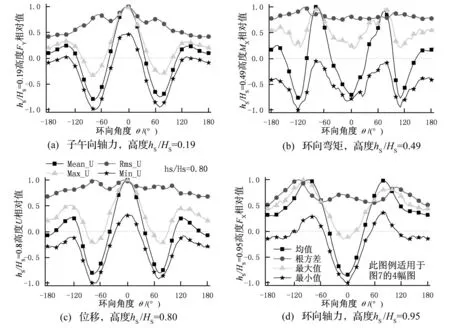
图5 各响应峰值因子的环向分布Fig.5 Gust factors for different responses

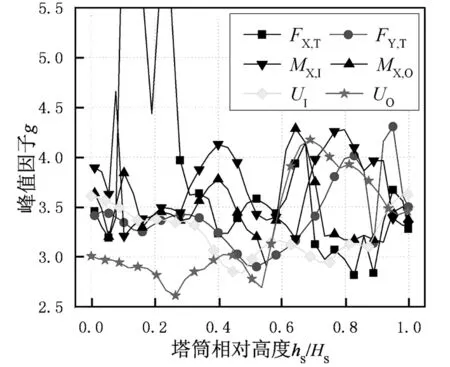
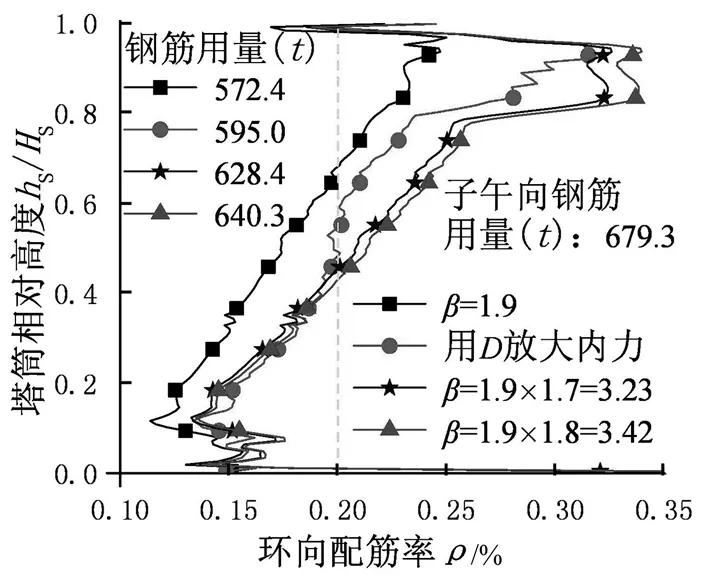
3.6

图5给出了几个断面不同响应的峰值因子g。可以看出，各响应g值的环向分布都有剧烈波动，但大都落在3.0～4.5之间，这也与前述研究者对风压和位移等指标的g值类似，但各响应g值的环向波动和幅值并不一致。总的看来，除塔顶局部区域的FY因均值较小而使g值波动较大外，其他高度g值波动剧烈程度依次为FX和MX、U和FY，这一次序也基本是其幅值大小的次序，这一现象在KASPERSKI的计算结果中亦有体现。分析其原因，FY不仅与本断面风压有关，还受本断面以上整个塔筒风压的共同影响[30]，这样，较大区域随机荷载的“区域平均效应”使FY的脉动性下降，并使其g的幅值和波动性最小。而FX和MX则主要受本断面风压的控制[30]，风压脉动性的“区域平均效应”较弱，所以其g的幅值和波动性较大。

图6 各响应动力放大系数的环向分布Fig.6 Dynamic amplification factors for different responses

对于动力放大系数D，不管是用式(1)和式(2)确定极值还是直接取最值为极值，各响应D值在塔筒表面的分布更为离散(图6)，部分位置响应的D值甚至在100以上。但D值在各高度断面的环向分布特征基本一致，这也是因为平均和脉动风压环向分布特征沿高度基本一致(图2)，从而使那些显著的D值都集中在几个确定的环向角度位置，如θ=±40°、±110°和±150°。而对比下文图7响应时程特征值的环向分布可知，在这些D值显著的位置，对应的响应均值都在零值附近。显然，在这些响应均值极小的位置，D的幅值并没有实际意义，但这些极大的D值却给实际应用带来困惑和不便，这也是冷却塔风振响应分析中的一个棘手问题。另外，不同响应D的分布模式和数值大小也有明显差异，这同样体现了不同内力和位移的不同动力响应特征。

2.2g和D的一维分布简化

对于冷却塔结构，如果仅着眼于风荷载或响应本身的特征而忽略了结构特性及其设计原则，上述复杂的g和D分布不仅将增加实际应用的难度，也会掩盖结构设计的关键问题。塔筒作为旋转轴对称结构，由于风和地震等荷载方向的任意性，在某个高度位置，塔筒整个环向的最不利内力可能出现在各个环向角度位置，因此设计中在一个高度位置仅取一组控制性荷载效应进行结构设计，并使此配筋计算结果用于整个圆周，也即配筋设计同样是旋转轴对称的。这就使得在配筋设计时，在一个确定的高度位置，仅需关注各响应时程极值的环向最大值即可。也即相当于整个环向仅需关注最不利的一个单元/节点即可，各荷载效应在一个高度只需要一个g和一个D，g和D只沿子午向变化，这样就可以将二维(环向、子午向)问题转变为一维(仅子午向)问题。另外，冷却塔塔筒的环向和子午向配筋设计是独立的，仍需对这两个方向独立分析。

一般来说，这种处理对于动力分析需要有一定条件：即响应时程均值和响应时程极值的环向分布模式应该类似，或者说时程均值和时程极值的环向最值应位于相同的环向位置。这样整个环向只需要关心此最不利位置处的响应即可，而冷却塔单塔表面平均和脉动风压分布恰使响应分布符合这一条件。图7给出了各响应的环向分布示意图，并且对响应的四个特征值分别以各自的相对值给出，使所有特征值在环向都分布在±1.0之间，并且对轴力以受拉为正，弯矩以外表面受拉为正，位移以向内凹陷为正。

从图7中可以看出，每个响应的时程均值和极值在环向的最大值位置基本重合，如高度hS/HS=0.19处的FY,其均值和极值重合于在θ=0°和θ=±75°位置，而此重合位置对应的动力放大系数则基本是整个环向的最小值(图6)。这也是因为各个响应的脉动响应沿环向分布较为均匀，如位移响应U(图7(c))，甚至响应均值和根方差的最大幅值出现在同一环向角度，如塔筒下部的FY在θ=0°位置(图7(a))。而最根本的原因还是单塔表面平均和脉动风压幅值显著的位置基本一致，均在迎风区和侧风区(图2)，并且这两个区域之间存在极高的相关性[24]。另外，在子午向，FY,T最大值与MY最大值的位置重合，均位于θ=0°位置，直接以θ=0°位置的内力参与荷载效应组合即可；在环向，尽管FX,T最大值与MX最大值的环向位置有偏差，但相距不远，均位于θ=60°～90°之间，亦可认为其重合以偏保守简化计算，且这样的简化对塔筒配筋几乎没有增加。

这种现象虽便于对结果的分析，但对结构本身却是不利的：均值响应最大的位置基本也是极值响应甚至是脉动响应最大的位置。需要说明的是，这一结论仅适用于单塔，群塔组合下，平均风压和脉动风压分布模式的变化或许使响应分布模式丧失这一规律。但不管单塔还是群塔，每个高度仍只有一组控制性荷载效应，每个响应在一个高度仍只需要一个g和一个D，只是g和D取值会发生变化。

图7 各响应时程特征值环向分布Fig.7 Latitude distributions of characteristic values for different responses

因此，基于结构响应控制指标特征值环向位置的一致性、结构设计中的轴对称方法以及内力组合模式的特点，也为了实用的方便，对于每个荷载效应，取其时程均值、时程根方差、时程最大/小值四个特征值的环向最大值作为本高度的特征值，反算本高度位置的g和D。这样，就将g和D的二维分布转变为仅沿子午向的一维分布。

图8给出了依此得到的g值一维分布。与图5不同，图8对FX和FY都仅给出拉力FX,T和FY,T的g，因为双向压力对结构设计均无影响，并且风荷载MY的幅值极小可以忽略；对环向弯矩MX和位移U，图8区分内凹和外凸两个方向分别给出，并以下标I、O区分。可以看出：①各响应g值的子午向分布虽有波动，但稳定性已较图5的环向分布有所提高；②不同响应的g值仍有差异，幅值从大到小依次为FX和MX、U和FY，这仍与图5一致。对于图8中各响应g值沿子午向的波动以及波动的差异，除荷载本身的脉动性以及各响应与荷载之间的关系不同外，结构振型的参与也是原因之一，因为冷却塔的各阶振型在子午向就表现为不同数量的谐波，并且各阶振型对各响应的参与程度也是不同的。

图8 各响应峰值因子的一维分布Fig.8 Meridian distributions of gust factors for different responses

尽管图8所给内力的g值仍沿高度有明显波动，但各内力只是在一定高度区域内控制结构设计：如FY,T在塔筒中下区域，FX,T仅在塔筒顶部区域，MX在整个塔筒范围，并且各内力在自己控制区域内的g值基本稳定。因此，可取本内力对结构设计影响区段范围内的g值作为整个高度的g值，这样也就可以将g沿高度的一维分布简化为一个单一的数值，仅依响应的不同而不同。同时，再考虑到环向和子午向在设计上的独立性，可分别对环向内力和子午向内力取gX=4.5和gY=3.75,对位移亦取gu=3.75。尽管塔筒顶部FY,T和塔筒底部FX,T的g值非常显著，但这两个内力在上述位置处均非结构设计控制内力，略低的g值并不会影响结构设计的安全。

图9分别给出了采用图8沿子午向波动的峰值因子g和单一峰值因子g对应的动力放大系数D。可以看出，不管采用哪种g值，各响应D值的幅值均有较大差异：其中以MX的D值最为显著，在3～6之间；FX,T和U基本在2附近，其中迎风点内凹位移UI的D值与的试验结果较为一致；而最为关键的FY,T最小，约在1.6附近，这一结果同样与KASPERSKI的研究结果一致。另外，在塔筒顶端0.2HS区域，由于各内力的均值极小，故D值均明显增加。

图9 各响应动力放大系数的一维分布Fig.9 Meridian distributions of dynamic amplification factors for different responses

2.3g和D的实际应用

探索风荷载动力放大系数D的实际应用首先要明确冷却塔的结构设计原则。作为工业构筑物，冷却塔所受荷载类型较少，使用阶段仅有自重、风、温度和地震4类作用。其壁厚主要根据稳定性要求确定，配筋区分环向和子午向独立设计，其中风荷载是子午向配筋的控制荷载，风荷载拉力与自重压力的差值是子午向配筋的决定因素，这也是已有研究关注FY,T的主要原因。在环向，其控制荷载主要是温度，其产生的MX是配筋的主要依据，但风荷载FX,T和MX的贡献不可忽略。据现行规范，常见荷载作用下，环向钢筋用量小于子午向，且差距随风速的增加而加大，环向配筋一般占总配筋量的35%～50%。

我国规范采用风振系数β表示冷却塔的风致动力效应并用于对静风荷载的放大，间接得到动力响应，并根据卢文达的研究对B类地貌取β=1.9，这就相当于对所有响应取动力放大系数D=1.9。实际上，卢文达是采用动力放大系数D表示风振效应，其算例也同样表明，同一内力的D沿高度变化，并且FX,T的D明显大于FY,T。因此，对所有位置的所有响应采用同一个D值显然不够合理。另外，在应用中必须区分动力放大系数D和风振系数β的差异：前者是表征响应动力效应的一个指标，后者则用于风荷载的放大以便于结构设计，是等效风荷载的概念，两者不能等代。但两者仍有密切关系，即首先经风振响应分析明确D，再以某响应为等效目标确定β。

鉴于不同响应风振效应的差异，对不同响应采用不同的D值直接对静风响应放大后参与荷载效应组合最为合理，但这并非现阶段的设计方法。为与现有设计方法保持一致，仍需结合结构设计对风振系数β进行分析取值。从图9可知，在子午向，尽管塔筒中下部FY,T的D值仅约为1.6，明显小于1.9，但此区域的FY,T最受关注，故仍可取D=1.9；塔筒上部FY,T的D值尽管显著增加，但此区域FY,T的幅值较小，一般最小配筋率ρmin=0.2%对应的构造配筋即可满足要求，即使采用图9(b)所示D值，配筋量仍小于构造配筋，故亦可取D=1.9。子午向压力FY,C的D值分布与FY,T类似且并非结构设计控制内力，其D值可同样随FY,T取1.9。对于MY，尽管其D值略大于1.9，但MY幅值极小，对结构设计的影响可以忽略，同样可对其取D=1.9。因此，对B类地貌，子午向内力均可取D=1.9，在子午向设计时即可仍按现行规范取β=1.9。

在环向，FX,T和MX对应的D值都大于1.9，且两者对结构设计均不可忽略。为保证结构设计安全，应提高环向设计的β值。因MX的D值显著大于FX，本应对这两个内力采用不同的D值，但这种方案与现行采用风振系数β的设计方法不一致，不便于工程应用。采实际上，MX和FX同时参与荷载效应组合进行结构设计，可在保证结构配筋的前提下对两者采用单一的D值，也即以配筋率为目标反推单一的D值。这实际上也是在等效风荷载分析中，用配筋量替代传统的内力或位移作为等效指标。对一座177 m高的冷却塔取基本风压0.4 kPa且保持壁厚不变的情况下，进行配筋计算分析，对环向内力统一取D=3.2所得环向配筋与对MX和FX分别采用图9(b)所示D值所得配筋分布相当(图10)。也即对B类地貌，配筋计算时可取β=3.2。

图10 不同方法所得环向配筋率Fig.10 Latitude reinforcement ratios got from different method

从图10还可看出，对环向配筋计算即使大幅提高β并不会引起塔筒材料用量的显著增加：在考虑ρmin后，β=3.2相较β=1.9对应的环向配筋用量仅增加5.6%，塔筒钢筋总用量仅增加2.6%。这是因为风荷载效应在环向配筋计算中的权重远小于温度效应。也正因如此，英国规范[31]虽指出环向内力的放大效应明显大于子午向内力，但对普通规模(<120 m)的冷却塔在环向采用构造配筋即可满足设计需要，故对环向和子午向采用了单一的荷载放大系数。然而，对于更高的冷却塔则需对环向内力的动力效应合理评定。

需要说明的是，上述环向和子午向独立的风振系数β仅用于塔筒配筋计算，而塔筒稳定性检算时同样需要β的参与，能否采用与配筋计算相同的β还需进一步研究。

3 结 论

首先经刚体模型风洞试验获得冷却塔表面风压，再采用时程方法进行结构动力响应计算并详细介绍了相关计算参数，最后结合冷却塔的设计方法对计算结果进行系统分析，提出了便于实用的风振系数。主结论要如下：

(1)作为典型的高耸空间薄壁结构，冷却塔塔筒的风振效应较为复杂，各响应的动力放大系数D极为离散，其空间二维分布也难以直接工程应用。但结合各响应的时程特征、塔筒自身旋转轴对称结构特点以及同样旋转轴对称的配筋设计原则，可以将塔筒的g值和D值从环向和子午向的二维分布简化为仅沿子午向的一维分布，由此所得各响应的D值已达工程实用量值。但各响应D值的幅值有较大差异：其中以MX最为显著，FX和U次之，FY最小。

(2)在一维简化后，环向内力FX和MX的D值有较大差异，但因两者在配筋设计中联合作用，因此可以在保证配筋安全的前提下对两者取单一的D值以作为风振系数β，这实际上也是在等效风荷载分析中，用配筋量替代内力作为等效指标。

(3)为与现行设计方法一致并保证配筋设计的安全，在一维简化的基础上，根据环向和子午向配筋设计的独立性，并考虑风荷载各内力在荷载效应组合及结构设计中的不同权重，在实际应用中更可针对各个内力分别取单一的g值，对D值也仅区分环向内力和子午向内力独立取值，由此所得D值即可用做传统意义的风振系数β。这样就可以沿用现有的设计方法，仅将现有单一风振系数β在环向和子午向分别取值。对于B类场地，对环向和子午向配筋计算可分别取β为1.9和3.2，并且环向β的大幅提高并不会引起塔筒材料用量的显著增加。

[ 1 ] ABU-SITTA S H. Hyperbolic cooling towers [J]. Engineering Journal, 1973, 56(10): 26-28.

[ 2 ] 黄志龙. 大型冷却塔结构分析的若干问题[J]. 力学与实践, 2012, 34(5): 1-5. HUANG Zhilong. Someproblems on structural analysis of cooling towers [J]. Mechanics in Engineering, 2012, 34(5): 1-5.

[ 3 ] 张军锋, 葛耀君, 赵林. 双曲冷却塔结构规范风荷载标准值对比[J]. 建筑科学与工程学报, 2011, 28(2): 52-61. ZHANG Junfeng, GE Yaojun, ZHAO Lin. Comparisons of nominal values of wind loads on hyperboloidal cooling tower [J]. Journal of Architecture and Civil Engineering, 2011, 28(2): 52-61.

[ 4 ] ABU-SITTA S H, HASHISH M G. Dynamic wind stresses in hyperbolic cooling towers [J]. Journal of the Structural Division, ASCE, 1973, 99(9): 1823-1835.

[ 5 ] ARMITT J. Wind loading on cooling towers [J]. Journal of the Structural Division, ASCE, 1980, 106(3): 623-641.

[ 6 ] NIEMANN H J, KÖPPER H D. Influence of adjacent buildings on wind effects on cooling towers [J]. Engineering Structures, 1998, 20(10): 874-880.

[ 7 ] 邹云峰, 牛华伟, 陈政清. 基于完全气动弹性模型的冷却塔风致响应风洞试验研究[J]. 建筑结构学报, 2013, 34(6): 60-67. ZOU Yunfeng, NIU Huawei, CHEN Zhengqing. Wind tunnel test on wind-induced response of cooling tower based on full aero-elastic model [J]. Journal of Building Structures, 2013, 34(6): 60-67.

[ 8 ] 陈凯, 魏庆鼎. 冷却塔风致振动实验研究[C]//第十一届结构风工程学术会议, 上海: 同济大学出版社, 2003: 177-182.

[ 9 ] 赵林, 葛耀君, 曹丰产. 双曲薄壳冷却塔气弹模型的等效梁格方法和实验研究[J]. 振动工程学报, 2008, 21(1): 31-37. ZHAO Lin, GE Yaojun, CAO Fengchan. Equivalent beam-net design theory of aero-elastic model about hyperbolic thin-shell cooling towers and its experimental investigation [J]. Journal of Vibration Engineering, 2008, 21(1): 31-37.

[10] 许林汕, 赵林, 葛耀君. 超大型冷却塔随机风振响应分析[J]. 振动与冲击, 2009, 28(4): 180-184. XU Linshan, ZHAO Lin, GE Yaojun. Wind-excited stochastic responses of super large cooling towers [J]. Journal of Vibration and Shock, 2009, 28(4): 180-184.

[11] 柯世堂. 大型冷却塔结构风效应和等效风荷载研究[D]. 上海：同济大学博士学位论文, 2011.

[12] 卢文达, 王养琪, 蓬静欣, 等. 双曲冷却塔的阵风响应[J]. 中国电机工程学报, 1982(1): 45-61. LU Wenda, WANG Yangqi, PENG Jingxin, et al. Response of hyperbolic cooling tower to turbulent wind [J]. Proceedings of the CSEE, 1982(1): 45-61.

[13] KASPERSKI M, NIEMANN H J. On the correlation of dynamic wind loads and structural response of natural-draught cooling towers [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 30(1/2/3): 67-75.

[14] 鲍侃袁. 大型双曲冷却塔的风荷载和风致响应理论分析与试验研究[D]. 杭州：浙江大学, 2009.

[15] KAPANIA R K, YANG T Y. Time domain random wind response of cooling tower [J]. Journal of Engineering Mechanics, 1984, 110(10): 1524-1543.

[16] BARTOLI G, BORRI C, ZAHLTEN W. Nonlinear dynamic analysis of cooling towers under stochastic wind loading [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 43(1/2/3): 2187-2198.

[17] ORLANDO M. Wind-induced interference effects on two adjacent cooling towers [J]. Engineering Structures, 2001, 23(8): 979-992.

[18] 余关鹏. 大型双曲冷却塔风荷载特性和风致干扰效应研究[D]. 杭州：浙江大学, 2010.

[19] 武秀根, 郑百林, 刘曙光, 等. 大型冷却塔的风致振动响应数值分析[J]. 力学季刊, 2011, 32(1): 91-97. WU Xiugen, ZHENG Bailin, LIU Shuguang, et al. Numerical analysis of wind induced response for large cooling tower [J]. Chinese Quarterly of Mechanics, 2011, 32(1): 91-97.

[20] 李旭, 李晓文. 超大冷却塔风振响应分析[J]. 建筑结构, 2014, 41(增刊1): 1414-1417. LI Xu, LI Xiaowen. Analysis of wind-induced dynamic response of super large cooling tower [J]. Building Structure, 2014, 41(Sup1): 1414-1417.

[21] 张相庭. 结构风工程[M]. 北京: 中国建筑工业出版社, 2006.

[22] 周晅毅. 大跨度屋盖结构风荷载及风致响应研究[D]. 上海: 同济大学, 2004.

[23] 火力发电厂水工设计规范(DL/T 5339—2006)[S]. 北京: 中国电力出版社, 2006.

[24] 张军锋, 葛耀君, 赵林, 等. 双曲冷却塔表面三维绕流特性及风压相关性研究[J]. 工程力学,2013, 30(9): 234-242. ZHANG Junfeng, GE Yaojun, ZHAO Lin, et al. Wind tunnel study on the three dimensional flow and spatial correlation properties of wind loads on hyperboloidal cooling towers [J]. Engineering Mechanics, 2013, 30(9): 234-242.

[25] 张军锋, 葛耀君, 赵林, 等. POD与MSM原理和应用的对比分析[J]. 力学与实践, 2013, 35(5): 69-78. ZHANG Junfeng, GE Yaojun, ZHAO Lin, et al. Comparative study on the principles and applications of POD and MSM [J]. Mechanics in Engineering, 2013, 35(5): 69-78.

[26] STEINMETZ R L, ABEL J F, BILLINGTON D P. Hyperbolic cooling tower dynamic response to wind [J]. Journal of the Structural Division, 1978, 104(1): 35-53.

[27] JUHASOVA E, BITTNAR Z, FISCHER O. Vibration characteristics of a cooling-tower shell [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1983, 12(2): 145-154.

[28] WINNEY P E. The modal properties of model and full scale cooling towers [J]. Journal of Sound and Vibration, 1978, 57(1): 131-148.

[29] JEARY A P, FRIDLINE D, WANG L. Dynamic stability considerations for a natural-draft cooling tower under repair with hurricane-force wind action [C]// 13th International Conference on Wind Engineering, 2011, Netherlands, Amsterdam.

[30] 张军锋, 葛耀君, 赵林. 双曲冷却塔结构特性新认识[J]. 工程力学, 2013, 30(6): 67-76. ZHANG Junfeng, GE Yaojun, ZHAO Lin. New perceptions on the structure behavior of hyperboloidal cooling towers [J]. Engineering Mechanics, 2013, 30(6): 67-76.

[31] BS 4485 Part 4. Code of Practice for Structural Design and Construction-Water Cooling Towers [S]. London: British Standard Institution, 1996.

Wind induced responses of a hyperboloidal cooling tower in time-domain and gust effect factor analysis

ZHANG Junfeng1,2, GE Yaojun2, ZHAO Lin2

(1. School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China;2. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

Studies were conducted for wind induced dynamic responses of a hyperboloidal cooling tower, gust factorgand dynamic amplification factorDof its different internal forces and displacements. The gust effect factorβ, a concept of the equivalent wind load used for structural design was included as well. The tower’s wind-induced dynamic analyses in time domain were conducted based on the wind pressure data obtained from wind tunnel tests on a rigid model of a large hyperboloidal cooling tower. The results showed thatgandDof all responses both vary greatly with tower shell positions in latitude and meridian directions, and therefore they can’t be applied in practice conveniently; however, the two dimensional distributions ofgandDcan both be simplified into one dimensional distributions just along meridian height; this simplification is based on the characteristics of time domain responses, structure behavior and structural design principles; meanwhile, the amplitudes ofDcan be applied practically but the application method is not consistent with that of the current design codes; furthermore, according to the structural design independence in latitude and meridian directions and different weights of wind induced internal forces in structural design, twoDs are adopted for the internal forces in latitude and meridian directions, respectively, but the former is much higher than the latter; consequently, the twoDs can be used asβs in the two directions, respectively in structural design as usual.

cooling towers; wind tunnel test; time-domain analysis; gust factor; dynamic amplification factor; gust effect factor

国家自然科学基金(51508523);中国博士后科学基金(2014M552016)

2015-08-25 修改稿收到日期：2015-12-28

张军锋 男，讲师，博士，1983年生

TU33+2; TU271.1

A

10.13465/j.cnki.jvs.2017.03.026