高层建筑屋顶广告牌风致响应分析
2017-03-09韩志惠陆文强谢壮宁
韩志惠, 陆文强, 顾 明, 谢壮宁
(1.上海市气象科学研究所,上海 200030;2.同济大学 土木工程防灾国家重点实验室,上海 200092;3.华南理工大学 亚热带建筑科学国家重点实验室,广州 510640)
高层建筑屋顶广告牌风致响应分析
韩志惠1,2, 陆文强2, 顾 明2, 谢壮宁3
(1.上海市气象科学研究所,上海 200030;2.同济大学 土木工程防灾国家重点实验室,上海 200092;3.华南理工大学 亚热带建筑科学国家重点实验室,广州 510640)
基于刚性模型测压风洞试验数据,采用时程分析法对高层建筑屋顶广告牌的风致响应进行了研究,并分析了单边布置、邻边布置、三边布置及四边布置广告牌对风致响应的影响。结果显示,高层屋顶广告牌单边布置时面板受力最大,而三边布置广告牌时面板受力最小;面板中间位置的斜撑单元对风荷载最为敏感,靠近面板迎风侧的立柱单元内力响应相对较大,面板中心位置的横向单元内力响应最大;不同的广告牌布置方式下,各类单元的阵风响应因子差别都不超过0.1。而同一种广告牌布置方式下各类单元之间的阵风响应因子差别最大为0.3;建议计算高层屋顶广告牌等效静力风荷载时,可偏保守地将阵风响应因子统一取为1.6。
高层建筑屋顶广告牌;风洞试验;风荷载特性;风致响应;阵风响应因子
高层建筑屋顶广告牌作为附属式广告设施的主要形式之一,在向公众传递信息的同时,也带来了诸多安全隐患。作为典型的风敏感结构,高层建筑屋顶广告牌表面风压气动特性不仅与结构自身外形有关,还直接受到所依附结构外形及相邻广告牌的影响,现有规范已无法满足结构设计人员的需求。目前复杂结构气动力特性研究的主要方法有风洞试验和数值模拟两种方法。LETCHFORD[1]采用风洞试验方法研究了高宽比、离地高度、来流风向等参数对单面矩形平板(广告牌)表面气动力的影响。PAULOTTO等[2]基于风洞试验研究了建筑群对框架式单面广告牌表面风荷载的影响。宋芳芳[3]采用数值方法方法对独立式、依附式户外广告牌的风压系数进行了模拟,发现斜风向风荷载风压系数分布要比顺风向风荷载更为不利。但是尚无研究人员采用风洞试验方法对高层建筑屋顶广告牌进行专业研究。
此外研究人员对这一类广告牌的风振特性也存在争议。高层建筑屋顶广告牌通常刚度大,余永济[4]认为设计时可以不考虑风振效应的影响,而大多数工程设计人员则参考《建筑结构荷载规范》[5]对高层(高耸)结构风振效应的相关规定。而沈之容等[6]则认为,在计算楼顶广告牌结构风振系数时,应取广告牌与下部房屋结构作为一个整体时的自振周期。显然,这些方法还值得商榷。
本文基于刚性模型测压风洞试验数据,采用时程分析法对高层建筑屋顶广告牌的风致响应进行研究,并对比分析单边布置、邻边布置、三边布置及四边布置广告牌对风致响应的影响,拟为高层建筑屋顶广告牌的抗风设计提供有参考意义的结论。
1 结构简介
屋顶广告牌结构型式主要是单面型式,附有广告的一面朝外,但是尺寸大小不一。宽度通常同建筑物宽度,而高度则需按照相关规范或规定设定,如上海市规定屋顶设置广告牌的高层建筑高度不得超过55 m,并且广告牌的高度不得超过5 m[7]。高层建筑多数是独栋结构,广告牌可绕建筑物屋顶四边设置,因此屋顶广告牌所受风荷载除了与结构自身外形有关外,还受到建筑物顶部外形的影响,而设置的多块广告牌之间也会互相产生干扰效应。为此, 本文设定4种屋顶广
告牌组合形式,分别为单边、邻边、三边以及四边布置(见图1),以面板1为主要研究对象来分析不同设置方式对广告牌风荷载特性及风致响应的影响。
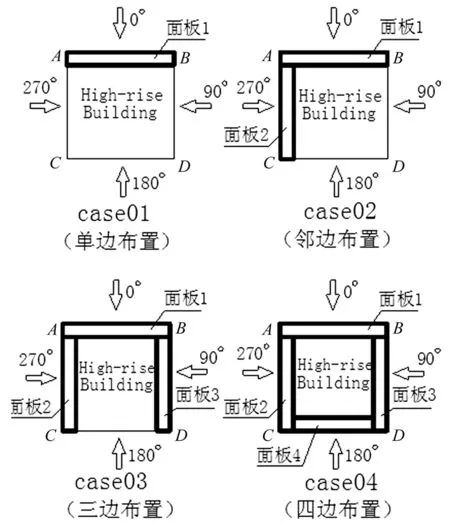
图1 高层建筑屋顶广告牌设置方式Fig.1 Locations of billboard on high-rise building roof
本文假设高层建筑屋顶的每块广告牌都为独立结构,即设置的多块广告牌之间没有力的传递。高层建筑为长宽高分别为30 m×30 m×55 m的标准长方体,横截面为正方形。每块广告牌的结构型式及构件参数相同,取值主要参考了文献[6,8]。单块广告牌由面板和支撑体系组成,其中面板为30 m×5 m的矩形形状,表面覆盖0.6 mm铁皮,面板骨架构件均为角钢L50×4;支撑系统中斜撑杆采用圆形钢管,直径为0.09 m,壁厚0.005 m;支撑系统中其他构件均采用角钢L63×5。构件材质均为Q235钢,如图2所示。
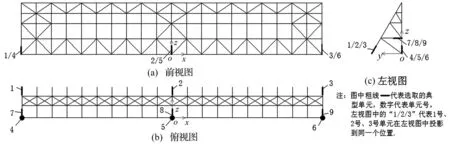
图2 单块广告牌结构示意图Fig.2 Configurations of billboard
2 风洞试验概况
风洞试验在同济大学土木工程防灾国家重点实验室的TJ-2 大气边界层风洞中进行。该风洞为闭口回流式矩形截面风洞,试验段尺寸为宽3 m、高2.5 m、长15 m。试验风场为C类地貌,采用粗糙元和尖劈实现。C类风场的平均风剖面指数为0.22,10 m处的名义湍流强度为0.23,风场模拟结果见图3。图中Z、Ztop分别为任意高度、模型顶部高度;U、Utop分别为任意高度风速、模型顶部高度风速;Iu为湍流度。试验模型几何缩尺比为1∶75,其中广告牌部分采用双层有机玻璃板制作,并以边密中疏、满布对称的双面对应方式进行测点布置。高层建筑部分采用木质薄板制作,没有布置测点。单块广告牌的测点数为55×2=110个。风向角定义见图1,试验风向角间隔取为15°,按顺时针方向增加,每种工况共24个风向角。
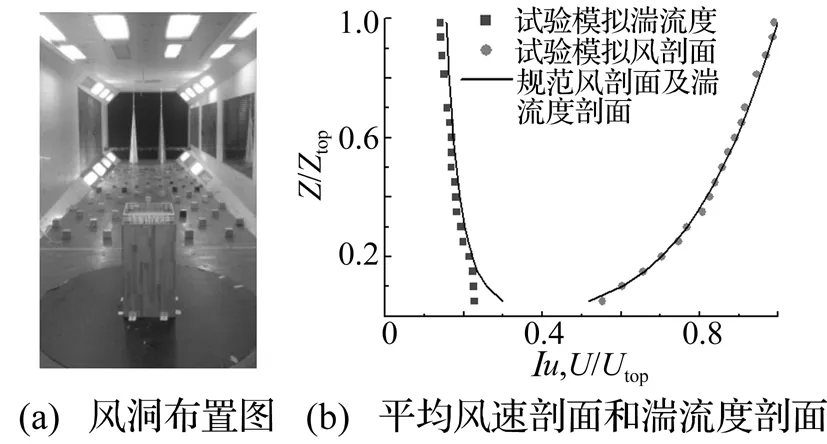
图3 风洞中模拟的C类风场Fig.3 Simulated wind field for terrain category of C
3 风荷载特性分析
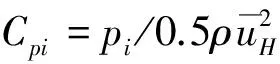
图4为高层建筑屋顶广告牌在4种布置方式下,面板1的合力系数平均值、均方差值随风向角的变化曲线。由于广告牌单边布置、三边布置、四边布置时都具有对称特性,而广告牌邻边布置时其表面风荷载在180°~360°风向角下结果小于0°~180°风向角,因此本文仅分析4种布置方式0°~180°风向角的风荷载特性。结果显示,4种工况下面板1的合力系数平均值随着风向角的变化规律相似,在0°~90°风向角间合力系数平均值为正值,并且随着风向角的增大而先增大后逐渐减小;90°风向角时,合力系数接近于0;在90°~180°风向角间,除了165°和180°风向角下工况4的面板1合力系数平均值为正值外,其余各个工况下面板1 的合力系数平均值均为负值,并且绝对值随着风向角的增大而先增大后减小。各工况下面板1的合力系数均方差值随风向角变化的总体趋势为先减小后增大。
单边布置广告牌时,面板1合力系数的平均值、均方差值在45°风向角下达到最大值,分别为1.34、0.25;邻边、三边布置广告牌时,面板1合力系数的平均值、均方差值都在15°风向角下达到最大值,分别为1.31、0.24和1.10、0.21;四边布置广告牌时,面板1合力系数的平均值、均方差值在0°风向角下达到最大值,分别为1.19、0.24。比较而言,高层屋顶广告牌单边布置时面板1的最不利风压最大,而三边布置广告牌时面板1的最不利风压最小。
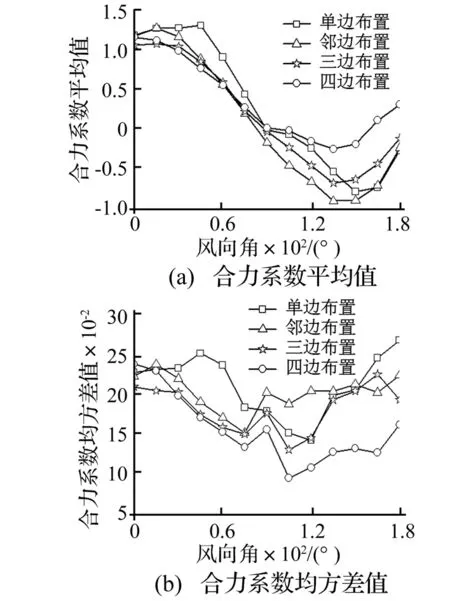
图4 高层建筑屋顶广告牌合力系数随风向角变化曲线Fig.4 Total pressure coefficients of billboard on high-rise building roof vs. wind direction
4 风致响应分析
4.1 时程分析方法简介
时程分析法就是对运动方程进行直接积分,仅在一系列离散的时间点上求运动方程的解。本文基于有限元软件平台,将风荷载时程作为外荷载作用于有限元模型上,采用Newmark逐步积分法计算结构的风致动力响应。结构的运动平衡方程可表示为
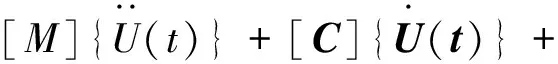
[K]{U(t)}={P(t)}
(1)
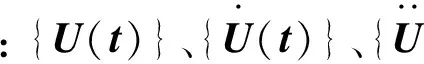
4.2 结构自振特性分析
图5给出单块广告牌的典型振型及自振频率。振型分析结果显示,结构的前三十三阶振型均表现为面板表面覆盖铁皮的局部振动,且模态分布密集。第三十四阶振型才出现结构整体的横向振动,自振频率为16.460 Hz,已经超出一般来流风的主频率。这是结构的整体刚度较大而表面覆盖铁皮的刚度相对较小导致的。
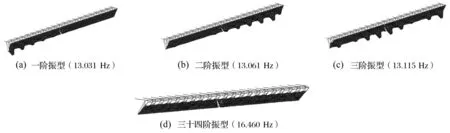
图5 自振频率和振型Fig.5 Frequency and modes
4.3 不同类型单元内力响应特性
高层建筑屋顶广告牌结构整体刚度大导致其立柱和横梁的位移较小,以单边布置条件下的风振响应计算结果为例,在最不利风向角下,面板结构顶部横梁的最大水平位移仅为3 mm。而屋顶广告牌的风毁事故调查结果也表明此类广告牌通常是由于面板骨架或支撑系统钢构件在压力作用下失稳而破坏,可见钢构件内力是此类结构稳定性的控制因素。因此,本文以单元的内力响应作为主要分析对象。
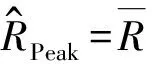
从图6(a)可以看出,在0°~90°风向角内,斜撑单元1、2、3都承受压力作用,内力响应平均值为负值;而在90°~180°风向角内则承受拉力的作用,内力响应平均值为正值,这与广告牌面板所受风荷载由压力转为吸力相对应。比较不同位置斜撑单元的内力响应可以发现,在大部分风向角下斜撑单元2的内力响应平均值、均方差值、峰值的绝对值都大于其他单元,其次是靠近迎风侧的斜撑单元1,响应最小的为远离迎风侧的斜撑单元3,说明位于面板中间位置的斜撑单元对风荷载最为敏感。斜撑单元2在45°风向角下承受的压力峰值最大,其平均值、均方差值、峰值分别为-6.15 kN、1.28 kN、-9.35 kN;在165°风向角下承受的拉力峰值最大,其平均值、均方差值、峰值分别为3.44 kN、1.44 kN、6.91 kN。
图6(b)显示,立柱单元在0°~180°风向角内都承受压力作用,内力响应平均值为负值,且绝对值随风向角变化逐渐增大。但是与斜撑单元内力相比,立柱单元内力整体偏小。靠近面板迎风侧的立柱单元4内力响应相对较大,其峰值响应在165°风向角下达到最大值,相应的平均值、均方差值、峰值分别为-0.86 kN、0.11 kN、-1.15 kN。
横向单元内力响应特性与斜撑单元相似,不再赘述。位于面板中心位置的横向单元8内力响应最大,其压力峰值在15°风向角下达到最大,相应的平均值、均方差值、峰值分别为-3.37 kN、0.71 kN、-5.15 kN;拉力峰值在150°风向角下达到最大,相应的平均值、均方差值、峰值分别为2.69 kN、0.74 kN、4.55 kN。
4.4 不同广告牌布置方式下单元内力响应特性
前文分析可知,单元2、4、8内力相应分别为斜撑单元、立柱单元、横向单元中最大者。本小节以这3个单元作为典型单元,分析不同广告牌布置方式对典型单元内力的影响,所施加的风荷载为不同广告牌布置方式下面板1的表面风压。图7给出不同广告牌布置方式下典型单元内力平均值、均方差值及峰值随风向角的变化曲线。
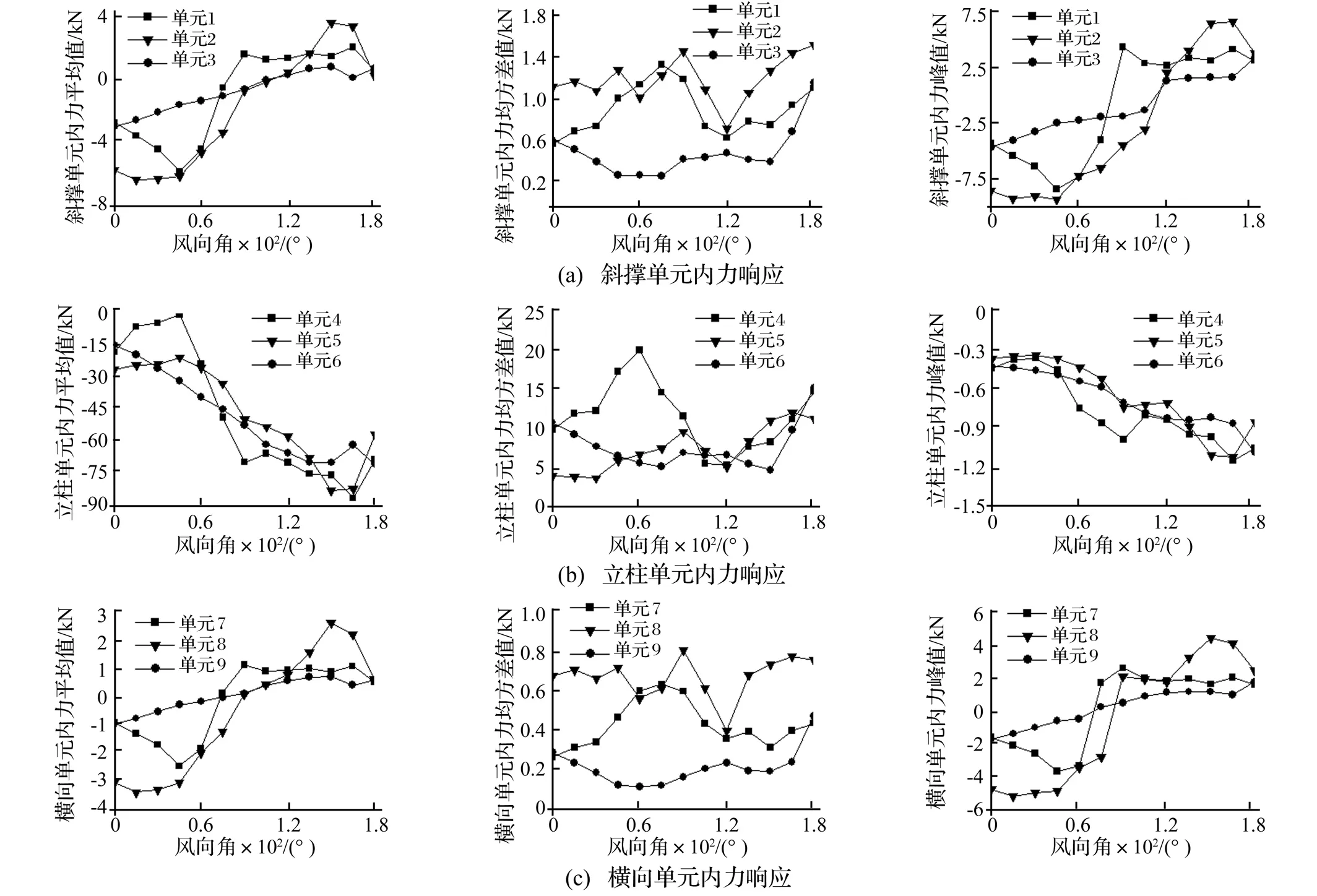
图6 不同类型单元内力响应随风向角变化曲线Fig.6 Force responses of different elements vs. wind direction
图7 不同广告牌布置方式下单元内力响应随风向角变化曲线Fig.7 Force responses of elements under different billboard location vs. wind direction
结果显示,不同广告牌布置方式下典型单元内力平均值、均方差值及峰值随风向角的变化趋势相似,仅仅在数值及最不利风向角上略有不同。细致的数据分析表明,在多数风向角下,单边布置条件下单元内力值较大,四边布置条件下单元内力值较小,其他两种布置方式下单元内力则居中。说明当广告牌仅在高层建筑屋顶单边布置时,由于来流在建筑边缘及广告牌边缘存在复杂的分离,导致广告牌风致响应较大,容易发生破坏,而增加广告牌数量会降低广告牌对风荷载的敏感性。
单边、邻边、三边、四边布置广告牌时,单元2的压力峰值分别在45°、15°、15°、0°风向角下达到最大值;单元4压力峰值分别在165°、165°、75°、75°风向角下达到最大值;单元8的压力峰值分别在15°、15°、15°、0°风向角下达到最大值。
4.5 阵风响应因子
图8给出了单边布置广告牌条件下斜撑单元2的内力响应在45°风向角下的功率谱密度曲线。由图可知,斜撑单元2的动力响应主要由背景部分提供,能量主要集中在低频处,在高频处没有出现共振峰值。这是因为高层屋顶广告牌的自振频率较大(第一阶自振频率为13.031 Hz,而第一阶整体振动频率为16.460 Hz),远大于一般来流风的主频率,难以激起任何的共振响应。其他类型单元的内力响应功率谱类似。
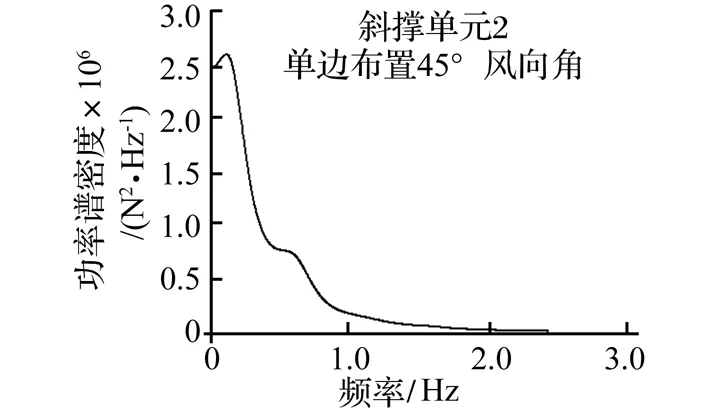
图8 典型单元内力响应功率谱曲线Fig.8 PSD of force responses of elements
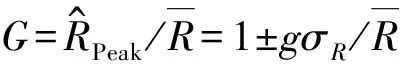
计算结果表明,斜撑单元2的阵风响应因子在1.46~1.52之间;立柱单元4的阵风响应因子在1.22~1.34之间;横向单元8的阵风响应因子在 1.52~1.59之间。不同的广告牌布置方式下,各类单元的阵风响应因子差别都不超过0.1。而同一种广告牌布置方式下各类单元之间的阵风响应因子差别最大为0.3。为方便结构设计人员使用,本文建议计算高层屋顶广告牌等效静力风荷载时,可偏保守地将阵风响应因子统一取为1.6。
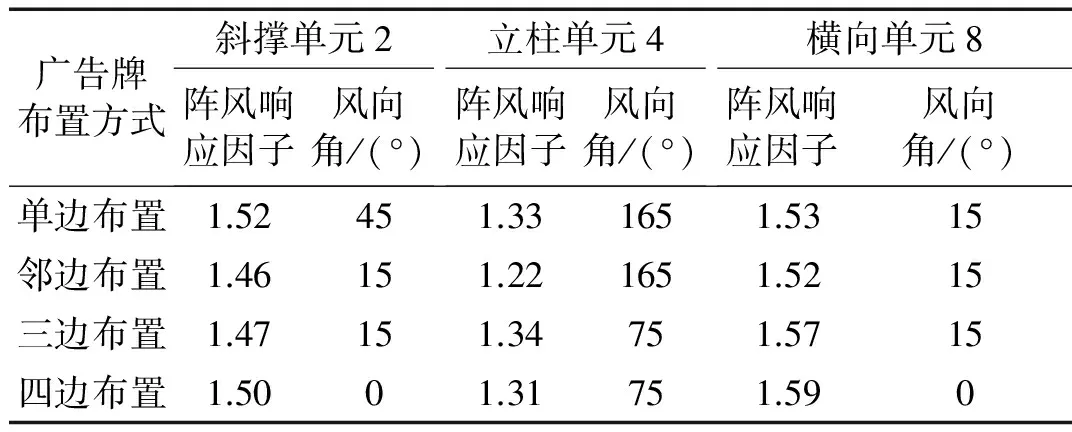
表1 典型单元内力响应阵风响应因子
5 结 论
本文基于刚性模型测压风洞试验数据,采用时程分析法对高层建筑屋顶广告牌的风致响应进行了研究,并分析了单边布置、邻边布置、三边布置及四边布置广告牌对风致响应的影响,得出以下主要结论:
(1)单边布置广告牌时,面板1合力系数的平均值、均方差值、峰值在45°风向角下达到最大值,分别为1.34、0.25、1.97;邻边、三边布置广告牌时,面板1合力系数的平均值、均方差值、峰值都在15°风向角下达到最大值,分别为1.31、0.24、1.91和1.10、0.21、1.62;四边布置广告牌时,面板1合力系数的平均值、均方差值、峰值在0°风向角下达到最大值,分别为1.19、0.24、1.79。比较而言,高层屋顶广告牌单边布置时面板1受力最大,而三边布置广告牌时面板1受力最小。
(2)面板中间位置的斜撑单元对风荷载最为敏感,靠近面板迎风侧的立柱单元内力响应相对较大,面板中心位置的横向单元内力响应最大。
(3)在多数风向角下,单边布置条件下单元内力值较大,四边布置条件下单元内力值较小,其他两种布置方式下单元内力则居中。
(4)不同的广告牌布置方式下,各类单元的阵风响应因子差别都不超过0.1。而同一种广告牌布置方式下各类单元之间的阵风响应因子差别最大为0.3。为方便结构设计人员使用,本文建议计算高层屋顶广告牌等效静力风荷载时,可偏保守地将阵风响应因子统一取为1.6。
[ 1 ] LETCHFORD C W. Wind loads on rectangular signboards and hoardings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(2): 135-151.
[ 2 ] PAULOTTO C, CIAMPOLI M, AUGUSTI G. Wind tunnel evaluation of mean wind pressure on a frame-type signboard[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94(5): 397-413.
[ 3 ] 宋芳芳. 几类风灾易损建筑台风损伤估计与预测[D]. 哈尔滨:哈尔滨工业大学, 2010.
[ 4 ] 余久济. 广告牌结构风荷载取值问题的研究[J]. 工业安全与防尘, 2001(2): 25-26. YU Jiuji. A study of values of wind-load of construction of advertisement columns [J]. Industrial Safety and Dust Control,2001(2): 25-26.
[ 5 ] 中国建筑科学研究院.建筑结构荷载规范:GB50009—2012[S].北京:中国建筑工业出版社,2012.
[ 6 ] 沈之容, 李冰心. 楼顶广告牌结构基本自振周期计算方法研究[J]. 建筑结构, 2012, 42(3): 75-77. SHEN Zhirong, LI Bingxin. Research on calculation method of basic natural vibration period of roof billboard structure [J].Building Structure, 2012, 42(3): 75-77.
[ 7 ] 上海市绿化和市容管理局. 户外广告设施设置技术规范:DB31/283—2015[S]. 2013.
[ 8 ] 中国工程建设标准化协会高耸构筑物委员会. 户外广告设施钢结构技术规程:CECS 148—2003[S]. 北京: 中国计划出版社, 2003.
Wind-induced responses of billboards on high-rise building roof
HAN Zhihui1,2, LU Wenqiang2, GU Ming2, XIE Zhuangning3
(1. Shanghai Institute of Meteorological Science, Shanghai 200030, China;2. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China;3. State Key Laboratory of Subtropical Building Science, South China University of Technology, Guangzhou 510640, China)
Based on rigid model wind tunnel tests, wind-induced responses of billboards on high-rise building roof were studied using the time history analysis method, and the influences of unilateral, adjacent bi-lateral, tri-lateral, and quadri-lateral billboard arrangements on the wind-induced responses were analyzed. The results showed that the wind loading on face panels is the maximum under unilateral arrangement, and the minimum under tri-lateral arrangement; the diagonal brace element at the middle position of face panels is most sensitive to wind loading. The internal force response of the vertical prop element near windward side of face panels is larger relatively, the internal force response of the lateral beam element at the middle position of face panels is the largest; under different billboard arrangements, the gust response factor differences of all kinds of elements are not more than 0.1, under the same billboard arrangement, their maximum difference is 0.3; a conservative gust response factor of 1.6 is suggested to calculate the equivalent static wind loads of billboards on high-rise building roof.
billboards on high-rise building roof; wind tunnel test; wind load characteristics; wind-induced response; gust response factor
华南理工大学风工程广东省普通高校重点实验室开放研究基金(1302)
2015-08-07 修改稿收到日期:2015-12-30
韩志惠 女,博士,1985年生
顾明 男,博士,教授,博士生导师,1957年生
TU312.1
A
10.13465/j.cnki.jvs.2017.03.006
