空气隔层对水下爆炸冲击波的缓冲效应

寇晓枫， 王高辉， 卢文波， 陈 明， 严 鹏

(武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

空气隔层对水下爆炸冲击波的缓冲效应

寇晓枫， 王高辉， 卢文波， 陈 明， 严 鹏

(武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

由于水下爆炸对结构的破坏能力比空中爆炸要强得多，因此针对水下结构的防护越来越受到重视。根据一维应力波在不同介质交界面的透射反射理论，从理论上分析了低波阻抗介质(如空气)对水下爆炸冲击波传播的影响。通过建立含空气隔层的水下爆炸全耦合模型，考虑水下爆炸冲击波与空气隔层及爆轰产物的动态相互作用，研究了空气隔层对水下爆炸冲击波的缓冲效应，揭示了空气隔层的运动发展过程。同时分析了空气隔层厚度及位置对水下爆炸冲击波缓冲效应的影响。结果表明：空气隔层距防护对象越近，防护效果越佳，具有重要的工程应用价值。

水下爆炸；空气隔层；缓冲效应；冲击波传播特性；结构防护

由于水的密度大，可压缩性小，对冲击波的传递效率高[1]。因此在相同药量下，水下爆炸的破坏能力比空中爆炸较强[2-3]。在预留岩坎、围堰拆除以及扩机工程等水下爆破产生的水下冲击波可能对水下建筑物(如水工大坝结构物)的安全性能造成影响。同时，近年来随着精确制导武器的快速发展和国内外意外恐怖袭击的日益频繁，当炸药或炸弹在水下爆炸时将对水下建筑物的安全性能造成巨大威胁。因此，如何有效提高水下建筑物的抗爆防护性能，降低水下冲击波的破坏效应，其研究成果具有重要的工程实用价值和理论意义。

当冲击波传播到两种介质交界面时会发生反射和透射现象，而两种介质的波阻抗之比对冲击波传播具有重要的影响。由于空气的波阻抗比水小很多，当水下冲击波传播到空气与水的交界面时，水下冲击波将主要在介质交界面处发生反射，其透射系数较小，只有少部分能量透射到空气介质当中[4-5]，可有效缓冲水下冲击波。因此，在工程实践中可采用空气隔层来削弱水下爆炸冲击波的破坏效应。目前，空气隔层的主要应用形式有气泡帷幕[6]，还有舰船的防雷舱[7]等。关于空气隔层衰减水下爆炸冲击波这一方面，已经有一些实验或者数值模拟成果。如贾虎等[8]通过实验分析表明空气隔层可以有效衰减冲击波峰值压力，可以有效降低水下爆炸冲击波的破坏效应；姚熊亮等[9]编制了多介质水下爆炸计算程序，结果表明，无论是接触爆炸还是非接触爆炸，空气隔层均可有效衰减冲击波；邵鲁中等[10]通过海边浅层水中钻孔爆破试验，实测得到了水下冲击波波形曲线及压力数据，表明气泡帷幕对特定频率的冲击波有良好的削弱效果；周睿等[11]基于实验结果，采用爆炸相似律理论，得到了适用于工程实际计算的经验表达式。以上研究主要体现在空气隔层对水下爆炸冲击波的峰值衰减方面，然而有关水下爆炸冲击波与空气隔层及爆轰产物的动态相互作用、空气隔层的运动发展过程、冲击波的缓冲机制等方面的成果较少。

本文首先从理论上分析了空气隔层对水下冲击波传播的影响。然后基于显式动力分析程序AUTODYN，建立了二维数值计算模型，分析了自由场中水下爆炸冲击波的传播特性，并与其相应的经验公式进行对比，验证了数值计算的可靠性。最后通过建立含空气隔层的水下爆炸全耦合模型，研究了水下爆炸冲击波在水与空气界面及水与爆轰产物界面处的传播规律和特性，揭示了空气隔层缓冲水下爆炸冲击波的机理，得到了空气隔层的运动发展过程，并研究了空气隔层厚度及位置对于水下爆炸冲击波缓冲效应的影响。研究成果可以为水下结构的防护设计提供参考。

1 水下爆炸的空气隔层缓冲理论及状态方程

1.1 空气隔层缓冲水下爆炸冲击波的理论分析

应力波在传播过程中，遇到两种介质的交界面时，应力波的一部分会从交界面反射回来，另一部分透过交界面进入第二种介质。因应力波的入射角不同，有垂直入射和倾斜入射两种情况，下面只考虑垂直入射的情况。

以一维弹性波为例，如图1所示，设弹性波从一种介质1传播到另一种介质2，介质与介质的交界面为A-A。当应力波到达交界面是垂直入射时，就会产生垂直反射和垂直透射。其反射应力波大小σr、透射应力波大小σt与入射应力波大小σi之间的关系为[12]

σr=Rrσi

(1)

σt=Rtσi

(2)

式中:Rr为应力波的垂直反射系数，Rt为应力波的垂直透射系数，且

(3)

由式(1)～式(3)表明，反射应力波和透射应力波的大小是交界面两侧介质波阻抗(ρc)之比的函数。

值得说明的是：以上分析是基于一维弹性波动理论，然而波在两种介质交界处的透射和反射规律从定性角度讲对任何类型的波(如流体中的冲击波、爆轰波等)也是成立的，因此上述分析对流体中的冲击波有一定的适用性。

根据上述理论分析，当冲击波传播到不同介质交界面时，可以分为三种情况：

(1)当两种介质的波阻抗相等，即ρ1c1=ρ2c2时，Rt=1，Rr=0。这说明两种介质波阻抗相等时，冲击波全部通过交界面进入第二种介质，不产生波的反射。由此可知，两种介质均为水时，冲击波不发生反射。

(2)如果n<1,即ρ1c1<ρ2c2时,则10。这说明冲击波从低阻抗介质入射到高阻抗介质时，反射波与入射波同号，而透射波强度强于入射波强度。当介质2的波阻抗与比介质1相比大很多时，可以认为n→0，就相当于弹性波在刚壁(固定端)的反射。这时有Rt=2，Rr=1。这说明反射冲击波的符号、大小与入射冲击波完全一样，透射冲击波大小是入射冲击波的两倍。

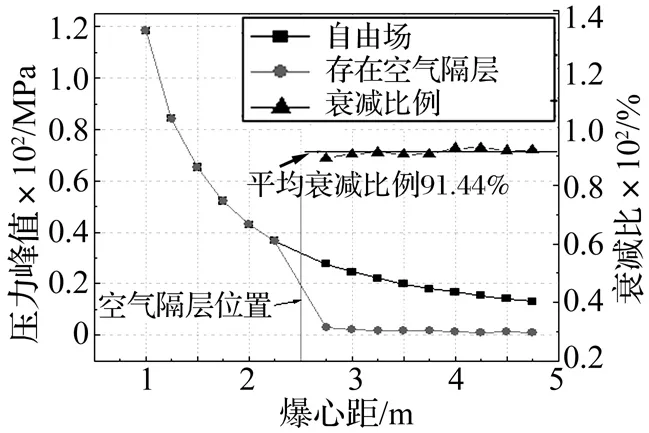
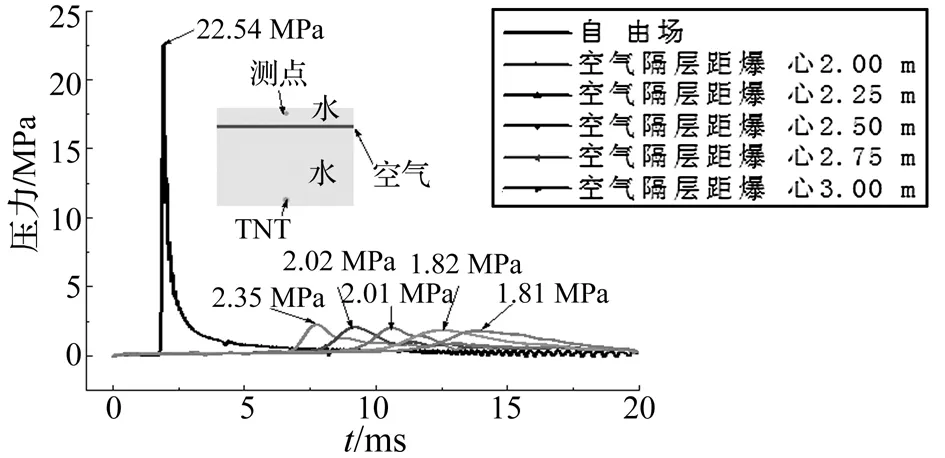
(3)如果n>1,即ρ1c1>ρ2c2时,则0

1.2 状态方程

1.2.1 炸药

TNT炸药密度为1.63 g/cm3,爆轰速度为6 930 m/s, C-J压力为21 GPa，爆轰产物状态方程采用标准的JWL状态方程态方程[13]。该状态方程可以用来计算由化学能转化成的压力，其压力和能量的关系可由式(4)确定：

(4)

式中:p为压力;A1、B1、R1、R2和w为材料常数;V为相对体积;E0为初始比内能。取A1=3.737 7×1011Pa,B1=3.747×1011Pa,R1=4.15,R2=0.9和w=0.35。

图1 纵波垂直入射Fig.1 The vertical incidence of longitudinal wave

1.2.2 水

水采用多项式状态方程进行描述，根据水的不同的压缩状态,状态方程有不同的形式。当(μ>0)即水压缩时，状态方程为：

P=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0e

(5)

当(μ<0)即水膨胀时，状态方程为：

P=T1μ+T2μ2+B0ρ0e

(6)

当μ=0，即水即不压缩也不膨胀时，状态方程为：

P=B0ρ0e

(7)

式(5)～式(7)中：P为水压力；μ为压缩比;μ=ρ/ρ0-1;A1为体积模量;A2、A3、B0、B1、T1、T2为材料参数；е为水的比内能；ρ0为水的密度，ρ0取999 kg/m3。取A1=2.2×106，A2=9.54×106，A3=1.457×107，B0=0.28，B1=0.28，T1=2.2×109Pa，T2=0。

1.2.3 空气

空气采用理想气体状态方程, 状态方程为：

(8)

式中:E为比内能，γ是绝热指数，γ取1.4,ρ0为空气初始密度，ρ0取1.225 kg/m3,ρ为当前密度。

2 自由场水下爆炸冲击波传播特性

为了验证数值计算的可靠性，并为后续的分析提供对比基础，建立了二维水下自由场轴对称计算模型(如图2所示)。模型计算尺寸为10 m×6 m，Y轴为计算模型的对称轴，单元网格尺寸为14.3 mm，计算模型单元数量为29.4万。球形TNT炸药装药量为8 kg，起爆点位于炸药中心。炸药和水均采用Euler算法。

图2 自由场水下爆炸计算模型Fig.2 Computational model of a free-field explosion in water

Euler算法在计算中采用有限体积法求解Euler控制方程，有限体积法是将微分方程先通过对网格中连续分布的单元控制体进行积分，然后对积分式进行离散化处理，再导出离散化方程的一种方法。为了模拟水下自由场爆炸和减小计算模型尺寸，在模型的截断处施加Transmission透射边界[14],使得冲击波在人工截断边界处无反射，以尽量消除人工截断边界的影响。

由于缺乏现场水下爆炸冲击波测试试验，将数值计算结果与Cole经验公式进行对比，以验证数值计算结果的可靠性。其水下爆炸冲击波压力时程曲线及峰值压力根据文献[15-16]总结的经验公式为

P(t)=Pme(-t/θ)

(9)

(10)

(11)

式中：Pm为冲击波峰值压力，Pa；t为从爆炸冲击波波面到达测点开始计时的时间，s；θ为冲击波指数误差时间常数；W为TNT炸药质量，kg；R为测点到爆心的距离，m；k1，α1，k2,α2是与炸药性能有关的经验参数，对于TNT炸药取值如下:k1=52.16 MPa，α1=1.13,k2=96.5×10-6，α2=-0.22。

图3给出了爆心距1 m处自由场水下爆炸数值计算和经验公式得到的压力时程曲线对比图。从图3可以看出数值计算得到的冲击波压力时程曲线与经验公式基本吻合，数值计算得到的波阵面到达时间及压力峰值与经验值相比基本相同。数值计算与经验公式得到的压力峰值大小分别为118.49 MPa、114.16 MPa, 数值计算得到的压力峰值与经验公式相比误差为3.79%。自由场水下爆炸冲击波压力时程曲线特性表现为爆炸冲击波波阵面到达之时，压力迅速达到峰值，然后以指数衰减至静水压力。数值计算得到的压力时程曲线并未按照规则的指数衰减，而是出现一定的锯齿性波动，其原因是数值模拟不能模拟冲击波的强间断性，通过引入人工黏性可以减少曲线的波动。

图3 爆心距1 m压力时程曲线Fig.3 Pressure histories at stand off distances of 1 m

图4给出了自由场水下爆炸数值计算和经验公式得到的不同爆心距处峰值压力对比曲线。从图4可知，在炸药附近处数值计算得到的冲击波峰值压力比经验值高，可能是由于数值计算和现场爆破试验均难以准确获得炸药附近处的冲击波压力峰值；而随着爆心距的增大，数值计算得到的压力峰值比经验公式小，主要由于数值模型的网格尺寸效应所致。但从整体上，数值计算得到的压力峰值与经验公式拟合较好。

图4 自由场水下爆炸冲击波压力峰值Fig.4 Peak pressure of shock wave from underwater explosion

3 空气隔层对于水下爆炸冲击波的缓冲机制

为了研究空气隔层对水下爆炸冲击波的缓冲机制，在自由场水下爆炸模型中加入空气隔层，建立了含空气隔层的水下爆炸全耦合模型(如图5所示)。空气隔层距起爆点的距离为2.5 m，厚度为0.1 m,模型的尺寸、炸药量、网格尺寸及边界条件均与图2一致。由于缺乏含空气隔层的爆炸冲击波传播经验公式以及现场试验，目前通过相关测试结果来直接验证含空气隔层耦合模型的可靠性仍存在一定的困难。然而含空气隔层的计算模型仍采用Euler算法进行求解，其网格尺寸和无反射边界等条件与自由场计算模型完全一致。并且Euler算法的节点在空间位置上固定不动，单元由节点连接而成，网格是一个固定的参考框架，水和空气材料在网格中可以随意流动，当存在空气隔层时填充相应的水和空气介质，此时水与空气以及空气与水自动耦合。因此建立的含空气隔层计算模型的可靠性基本可以得到保证。

图5 含空气隔层的计算模型Fig.5 Computational model with air interlayer

图6给出了炸药水下起爆后，爆轰产物及空气隔层的运动发展过程图。炸药在水下爆炸后，瞬间变为高温高压的爆轰产物(气泡)。随着冲击波向外传播，气泡内的压力迅速降低，同时气泡不断向外膨胀。水下爆炸冲击波传播至空气与水的交界面处时，入射冲击波在交界面处产生反射稀疏波和透射冲击波。在入射冲击波、反射稀疏波、透射冲击波的作用下，正对爆源位置的空气隔层质点将最先运动。同时由于气泡向外迅速膨胀，将压缩气泡周围的水介质，使其向四周运动，从而使得正对爆源位置的空气隔层逐渐被压缩变薄，向两侧运动，如图6(c)～图6(e)所示。随着气泡的继续膨胀，正对爆源位置的空气隔层逐渐被冲开，如图6(f)～图6(h)所示。从图6还可看出，炸药起爆后初始时刻，气泡膨胀速度较快(见图6(a)～图6(c))；而随着爆轰产物压力的下降以及空气隔层反射的冲击波与气泡相互作用，使得气泡膨胀缓慢(见图6(d)～图6(h))。

图6 空气隔层及爆轰产物的运动发展过程图Fig.6 Development process of air interlayer and denotation products

图7给出水下爆炸冲击波传播的压力云图。从图7可以看出，当炸药在水下起爆1.4 ms后，水下爆炸产生的冲击波传播至空气与水的交界面处(见图7(a))，由于水介质的波阻抗远大于空气介质，入射压缩波将在交界面处反射成为拉伸波(Prandtl-Meyer稀疏波)，稀疏波沿与入射波相反的方向向炸药中心传播。同时压缩波以透射波的形式向空气介质传播，且透射波的强度比入射波要小很多。因此在图7(b)～图7(d)中在空气以及空气后面水体基本看不到透射波的传播。由于水不能承受任何拉应力，在交界面处反射的稀疏波使附近的压力迅速下降，当压力下降到负压时，将在空气与水交界面附近形成气穴现象(见图7(b))，图中的负压即为气穴范围。随着稀疏波的继续传播，气穴将不断发展。当稀疏波传播至爆轰产物处时，将与气泡发生动态耦合作用，由于水介质的波阻抗远大于爆轰产物介质，稀疏波将在水与爆轰产物的交界面发生反射成为压缩波，使得气泡周围的水压力上升(见图7(c))。随着反射冲击波的继续传播，将再次与空气隔层发生作用(见图7(d))。在自由场条件下，气泡脉动压力往往发生在冲击波传播后的数十毫秒至数百毫秒。然而当空气隔层位于爆轰产物附近处时，由于气泡与冲击波的动态相互作用及周边水压力的变化，气泡膨胀将有别于自由场条件，导致脉动压力提前出现(见图7(e))。当气泡脉动压力传播到被冲开的空气隔层处时，由于脉动压力与周边空气隔层的相互作用，使得被冲开的空气隔层中心处出现压力集中现象(见图7(f))。

图7 水下爆炸冲击波传播过程Fig.7 Underwater explosion pressure wave propagation at different times

为了研究空气隔层对水下爆炸冲击波传播特性的影响，图8给出了空气隔层与炸药之间区域内测点(点1、点2)和空气后区域测点(点3)的压力时程曲线，并将其与自由场水下爆炸的结果进行对比，其中点1，点2，点3的爆心距分别为1.0 m，2.4 m，2.7 m。由图8(b)和图8(c)可知，当冲击波传播至空气隔层处时，由于水介质的波阻抗远大于空气介质，将反射形成稀疏波(第一次反射波)，使得爆源与空气隔层之间的测点压力迅速下降(即水面切断现象)，出现负压阶段。在第一次反射波到达测点之前，压力时程曲线与自由场水下爆炸完全相同。当反射的稀疏波传播至爆轰产物处时，将与爆轰产物发生动态耦合作用，由于水介质的波阻抗远大于爆轰产物，将使得稀疏波在爆轰产物与水的交界面处反射形成压缩波(第二次反射波)，第二次反射波沿着与第一次反射波相反的方向传播。由于第一次反射波在传播过程中大部分能量从爆轰产物的两边耗散，因此第二次反射波的强度远小于第一次反射波。第二次反射波冲击波传播至空气隔层与水的交界面处时将再次发生反射形成第三次反射波(稀疏波)。随着爆轰产物的不断膨胀，爆轰产物大约于t=8.2 ms到达点1，因此点1在大约t=8.2 ms后，压力时程曲线完全变为水平(见图8(b))。由于反射冲击波与爆轰产物的相互动态作用，以及气泡周围水压力的不断变化，使得气泡脉动压力提前出现，如图8(c)～图8(d)所示。从图中可以看出，相比于冲击波具有峰值压力大持时短的特点，气泡脉动压力具有峰值压力小持时较长的特点。

图8 不同测点的压力时程曲线Fig.8 Pressure histories at targets

图9给出了存在空气隔层时沿程峰值压力与自由场的对比以及衰减比例。从图9可知，爆源与空气隔层之间区域测点的压力峰值与自由场相比完全相同，而空气隔层后区域测点的压力峰值与自由场相比有了明显衰减。在爆心距2.75 m处压力峰值由自由场的27.70 MPa衰减到了2.95 MPa，压力峰值衰减比例为89.34%；在爆心距4.75 m处压力峰值由自由场的13.17 MPa衰减到了1.23 MPa，压力峰值衰减比例为92.21%；在空气隔层后区域的测点(爆心距2.75 m～4.75 m的范围内)冲击波压力峰值平均衰减比例为91.44%。说明空气隔层对水下爆炸冲击波具有明显的缓冲效应，可有效降低水下爆炸冲击波的压力峰值。

图9 存在空气隔层时沿程压力峰值Fig.9 Peak pressure of explosion with the existence of air interlayer

4 空气隔层厚度及位置对于水下爆炸冲击波缓冲效应的影响

4.1 空气隔层厚度的影响

为了研究空气隔层厚度对水下爆炸冲击波缓冲效应的影响，分别建立了空气隔层厚度为0.050 m、0.075 m、0.100 m、0.125 m、0.150 m五种水下爆炸全耦合模型。除空气隔层厚度外，空气隔层距爆心的距离、模型的尺寸、炸药量、网格尺寸及边界条件均与图5相同。

图10给出了在不同空气隔层厚度条件下空气隔层外测点(爆心距3 m)的冲击波压力时程曲线对比图。由图10可知，空气隔层厚度对水下爆炸冲击波的缓冲效应具有一定的影响。当空气隔层厚度分别为0.050 m、0.075 m、0.100 m、0.125 m、0.150 m时，压力峰值大小分别为2.89 MPa、2.38 MPa、2.25 MPa、2.16 MPa、2.15 MPa，压力峰值到达时间分别为t=6.2 ms、t=8.3 ms、t=10.3 ms、t=12.4 ms、t=14.3 ms。空气隔层厚度越大，空气隔层被冲开所需的时间越长，能量耗散的越多，导致空气隔层外测点的压力越低，说明增大空气隔层厚度可以提高防护效果。

同时可以看出，空气隔层厚度为0.075 m时测点的压力峰值相比于0.05 m厚度的空气隔层减小了17.6%；空气隔层厚度为0.100 m时测点的压力峰值比空气隔层厚度为0.075 m时减小了5.5%；空气隔层厚度为0.125 m时测点的压力峰值比空气隔层厚度为0.100 m时减小了4.0%；空气隔层厚度为0.150 m时测点的压力峰值比空气隔层厚度为0.125 m时仅减小了0.5%。说明当空气隔层厚度较小时，对冲击波的缓冲具有一定的影响，当继续增大空气隔层厚度时，缓冲效果越来越弱。

4.2 空气隔层位置的影响

为了研究空气隔层的位置对水下爆炸冲击波缓冲效应的影响，分别建立了空气隔层距炸药中心距离为2.00 m、2.25 m、2.50 m、2.75 m、3.00 m五种水下爆炸全耦合模型。除空气隔层的位置外，空气隔层的厚度、模型的尺寸、炸药量、网格尺寸以及边界条件均与图5相同。

图11给出了在不同空气隔层位置条件下空气隔层外测点(爆心距3.2m)的冲击波压力时程曲线对比图。从图11可知，空气隔层位置对冲击波的缓冲效应也具有一定的影响。当空气隔层距爆心的距离分别为2.00 m、2.25 m、2.50 m、2.75 m、3.00 m时，压力峰值大小分别为2.35 MPa、2.02 MPa、2.01 MPa、1.82 MPa、1.81 MPa，压力峰值到达时间分别为t=7.8 ms、t=9.3 ms、t=10.7 ms、t=12.3 ms、t=13.6 ms。空气隔层距炸药越远，作用于空气隔层的冲击波压力越小，空气隔层被冲开所需的时间越长，能量耗散的越多，导致空气隔层外测点的压力越低，说明空气隔层离防护对象越近，防护效果更佳。

图10 不同空气隔层厚度下的冲击波压力时程曲线Fig.10 Pressure histories in different thickness of the air interlayer

图11 不同空气隔层位置下的冲击波压力时程曲线Fig.11 Pressure histories in different locations of air interlayer

5 结 论

本文先从理论上分析了空气隔层对水下爆炸冲击波缓冲效应的基本原理，然后基于AUTODYN显式动力分析程序，建立了含空气隔层的水下耦合数值计算模型，研究了空气隔层对水下爆炸冲击波的缓冲机制。主要得到如下结论：

(1)由于冲击波与空气隔层的相互作用，以及气泡膨胀导致周边水介质的运动，空气隔层将被逐渐冲开。

(2)受空气隔层的影响，反射冲击波与气泡发生动态耦合作用，气泡周围水压力不断变化，使得气泡膨胀条件有别于自由场，导致气泡脉动压力提前出现。

(3)空气隔层厚度和位置对水下爆炸冲击波压力峰值的缓冲效应均有一定的影响。从结构防护的角度上来说：空气隔层厚度并非越厚防护效果越好；空气隔层离防护对象越近，防护效果更佳。

在实际应用当中，气泡帷幕是水和气泡的复杂混合物，完全的空气隔层难以做到。因此研究真实的气泡帷幕对水下爆炸冲击波的缓冲效应将在今后进一步研究。

[ 1 ] 高建华，陆林，何洋扬.浅水中爆炸及其破坏效应[M].北京：国防工业出版社，2010：20-21.

[ 2 ] RAJENDRAN R, LEE J M. Blast loaded plates[J].Marine Structures,2009,22(2):99-127.

[ 3 ] 张社荣，孔源，王高辉. 水中和空中爆炸冲击波传播特性对比分析[J]. 振动与冲击，2014，33(13)：148-153. ZHANG Sherong, KONG Yuan, WANG Gaohui. Comparative analysis on propagation characteristics of shock wave induced by underwater and air explosions [J]. Journal of Vibration and Shock, 2014，33(13)：148-153.

[ 4 ] WANG Gaohui,ZHANG Sherong,YU Mao, et al. Investigation of the shock wave propagation characteristics and cavitation effects of underwater explosion near boundaries[J].Applied Ocean Research,2014,46(2):40-53.

[ 5 ] PETROV N V,SCHMIDT A A. Multiphase phenomena in underwater explosion[J].Experimental Thermal and Fluid Science,2015,60:367-373.

[ 6 ] 余英. 气泡帷幕在三峡工程RCC围堰爆破拆除中的应用[J].水电与新能源,2010(4):8-11. YU Ying. Application of bubble curtain in blasting-demolition of RCC coffer dam of TGP[J]. Hydropower and New Energy,2010(4):8-11.

[ 7 ] KIM C H, SHIN Y S. Numerical simulation of surface shield effects to water blast wave[J]. Ocean Engineering, 2013, 60: 99-114.

[ 8 ] 贾虎，沈兆武.空气隔层对水中冲击波的衰减特性[J].高压物理学报，2012，32(1)：61-66. JIA Hu，SHEN Zhaowu. An investigation into attenuation of underwater shockwave by air interlayer[J].Explosion and Shock Waves，2012，32(1)：61-66.

[ 9 ] 姚熊亮，杨文山，初文华,等. 水中空气隔层衰减冲击波性能研究[J]. 高压物理学报，2011，25(2)：165-172. YAO Xiongliang, YANG Wenshan, CHU Wenhua, et al. Research on performance of the underwater air buffer weakening shock wave[J].Chinese Journal of High Pressure Physics, 2011，25(2)：165-172.

[10] 邵鲁中，龙源,孙远征,等. 削弱水下钻孔爆破水中冲击波负面效应的试验研究[J]. 工程爆破，2008，14(3)：13-17. SHAO Luzhong, LONG Yuan,SUN Yuanzheng, et al. Experimental investigation of weakening negative effect of shock wave in water of underwater drilling blasting[J]. Engineering Blasting，2008，14(3)：13-17.

[11] 周睿，冯顺山. 气泡帷幕对水中冲击波峰值压力衰减特性的研究[J]. 工程爆破，2001，7(2)：13-17. ZHOU Rui, FENG Shunshan. Study on weakening peak pressure of underwater shock wave by bubble curtain[J].Engineering Blasting，2001，7(2)：13-17.

[12] 王玉杰.爆破工程[M].武汉：武汉理工大学出版社，2009：116-117.

[13] ANSYS Inc.AUTODYN user manual version13[Z]. 2010.

[14] Century Dynamics Inc. AUTODYN theory manual version 4.3.Concord,CA:Century Dynamics[Z]. 2003.

[15] COLE R H. Underwater explosions[M]. New York: Dover Publications Inc.,1948.

[16] BJØRNØ L, LEVIN P. Underwater explosion research using small amount of chemical explosives[J]. Ultrasonics, 1976，14(6):263-267.

Mitigation effects of air interlayer on underwater explosion shock wave

KOU Xiaofeng, WANG Gaohui, LU Wenbo, CHEN Ming, YAN Peng

(State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China)

Underwater structure protection receives increasing attention due to more damages in structures under underwater explosion, compared to those under explosion in air. Based on the theory of one-dimensional stress wave transmitting and reflecting at the interface between two medium, the influences of low impedance medium, such as, air on underwater explosion shock wave propagation were analyzed. The fully coupled model for underwater explosion containing air interlayer was established. Considering the dynamic interaction among underwater explosion shock wave, air interlayer and detonation products, the mitigation effects of air interlayer on underwater explosion shock wave were investigated. The development process of air interlayer was revealed. At the same time, the influences of thickness and location of air interlayer on its mitigation effects on underwater explosion shock wave were analyzed. The results showed that the closer the distance between airlayer and the projected object, the better the protection effects. The results had important engineering application values.

underwater explosion; air interlayer; mitigation effect; shock wave propagation characteristics; structure protection

国家自然科学基金项目(51125037;51509189)；中国博士后科学基金资助项目(2015M572197)；中央高校基本科研业务费专项资金资助(2042015KF0001)

2015-11-23 修改稿收到日期：2016-01-15

寇晓枫 男，硕士，1991年生

王高辉 男，博士，讲师，1986年生 E-mail:wanggaohui@whu.edu.cn

TV312

A

10.13465/j.cnki.jvs.2017.03.002