基因组学数据的网络构建与分析方法*

哈尔滨医科大学卫生统计学教研室(150081) 王文杰 侯 艳 李 康

·综述·

基因组学数据的网络构建与分析方法*

哈尔滨医科大学卫生统计学教研室(150081) 王文杰 侯 艳 李 康△

基因组学数据具有超高维数、变量间作用关系复杂的特点，对其进行数据分析的方法研究面临巨大的挑战[1]。网络研究能够直观地反映出基因之间的相互作用关系，这不仅有助于特征标志物的筛选，增加筛选结果的可解释性，而且还能从分子水平阐述复杂的生物过程及各疾病的发病机制[1-2]。基因调控网络推断的本质是在不同影响因素条件下，通过测序得到各基因表达水平，利用各种方法和统计学指标，对不同基因表达的依赖关系进行衡量并排序，从而构建出潜在的基因调控网络，还原出网络的拓扑结构[3]。本文对近年新提出和发展的几种主要的网络分析方法做一综述。

网络推断方法

1.基于互信息的网络分析

两个变量关系的分析可以使用Pearson相关系数和Spearman相关系数的计算方法。然而，由于基于相关系数的方法无法识别表达模式之间更复杂的统计依赖关系(如非线性关系)，因此提出了基于互信息(mutual information,MI)的网络构建方法[4]。互信息可以看成是一个随机变量包含另一个随机变量信息量大小的统计量。两个基因间的互信息值可用于描述两基因间的统计相关性的大小，MI值大于给定阈值则认为相应的两个基因有调控连接[4-6]。采用MI衡量变量间的关联性时，要求数据为离散型数据，如果检测结果为连续型变量(如基因的表达水平)，则需要用光滑的样条函数来计算互信息[7]。一些研究者在互信息理论的基础上提出了用来区分网络中直接和间接相互作用边的改进方法，主要有环境相关似然度算法(context likelihood of relatedness,CLR)和准确胞状网络重建算法(algorithm for the reconstruction of accurate cellular networks,ARACNE)。其中，CLR算法是根据所计算出的MI值的经验分布修改MI得分，ARACNE算法则是利用互信息理论中的数据处理不等式(data processing inequality)这一性质，以每三个基因为搜索单元，将三个基因中的间接边过滤掉，具体算法如下：

(1)基础的互信息算法 两个随机的基因变量(x,y)的互信息值为

(1)

其中，I(x;y)代表基因x和基因y间的互信息，p(x)和p(y)分别为基因x和基因y的边际概率分布，p(x,y)为两基因的联合概率分布[5]。由于互信息统计量的计算要求数据为离散型，而微阵列得到的基因表达数据为连续型，因此需要先使用B样条平滑函数(B-spline smoothing)和数据离散化方法将数据离散化[7]。最后按照转录因子与目标基因间的互信息值大小排序，构造出网络结构。

(3)准确胞状网络重建算法(ARACNE) 不同于CLR算法，ARACNE算法是在两随机变量的互信息值基础上，通过修剪作用滤除互信息值较小的间接边[6]。其基本思想：首先使用高斯核估计量来估计互信息值[9]，与公式(1)不同的是，两个基因(x,y)间的互信息值通过使用二元标准正态密度函数，将概率的计算转变为函数的计算，公式如下：

(2)

其中，N为样本量，f(xi)和f(yi)分别表示随机变量基因x和y的边际概率转化成的高斯核函数，f(xi,yi)表示随机基因变量x和y的联合概率转化成的高斯核函数。根据上述公式，在计算出一个由任意两个输入基因x,y的互信息值MIxy组成的矩阵后，根据大偏差理论(large deviation theory)[10]，计算出所求的互信息值MIxy大于设定的阈值的概率，将大于阈值且显著的边保留，移除不显著的边，从而构建出网络结构。

以往基于互信息的网络构建方法存在一定的局限性，即当两基因间存在一个或多个中介基因时，这两个基因间便存在间接调控关系，导致网络推断性能评价中的假阳性率的上升。为此ARACNE算法基于数据处理不等式的理论，对选入的边进行修剪[10]，即在一个已知的基因调控网络中，数据处理不等式会删除那些间接边作用。例如对于一个简单的网络(gi↔gj,gj↔gk,gi↔gk)，如果I(gi;gj)≤min[I(gi;gk),I(gj;gk)]，则gi和gj之间的边将视为间接边被修剪移除。ARACNE算法对选入的调控关系中所连接的间接边结构的三个基因进行搜索识别，并移除三条边中互信息值最小的边，经过修剪后的调控边再根据其互信息值进行排序。

对于结构较为简单的网络，只要高斯核估计计算的互信息值MIij准确，则由ARACNE算法构建出来的网络将能准确地移除间接边，对于所连接的两基因(i,j)间的互信息值和任意一个中间基因k，都能保证Iij≥min(Ijk,Iik)。因此，在互信息基础上通过数据处理不等式修剪后的ARACNE算法，能够更准确地推断基因调控网络。Chávez等人在研究拟南芥根的转录调控关系时，使用了ARACNE算法构建其调控网络结构，成功验证了之前相关研究提出的根转录模型，并基于此网络结构提出了SHORT ROOT/SCARECROW和PLETHORA通路上的新转录因子[11]。

当网络结构较为复杂时，如基因i和j间可能存在不止一个中介基因，或者当基因i和基因j在三个基因对(i,j,k)中为直接作用，而在另外的三个基因对(i,j,p)中为间接作用的情况下，ARACNE算法将无法识别基因i和基因j的相互作用关系。在此基础上，Jang提出了高阶ARACNE算法，其不仅考虑了两基因间的一阶间接作用，还通过高阶数据处理不等式来处理更高阶的间接作用，因此能够识别两基因间更多的中介基因，显著提高了复杂调控网络推断的准确性[12]。

2.动态贝叶斯网络构建方法

贝叶斯网络是一种概率图形模型，它以有向无环图的形式反映了一组变量之间潜在的依赖和独立关系[13]。有向无环图中，如存在一条从节点A指向节点B的有向边，那么有向边所指向的B节点称为子节点，A节点称为父节点。若两节点之间没有直接相连的边则表示这两个节点相互独立，这就是贝叶斯网络的主要原理，称为马尔科夫条件。根据马尔科夫条件，每个节点的条件分布概率只与其父节点有关，这样能够大大地简化整个网络的联合概率分布，使得其计算上可行。对于一个贝叶斯网络图，记随机变量集为X={X1,X2,…,Xn}，Xi代表网络图中对应的节点，Pa(Xi)代表Xi节点处的父节点集，则贝叶斯网络为指定集合X的唯一联合概率分布

(3)

为确定以上的联合概率，需要确定所有上诉式中出现的条件概率，所有的这些条件概率组成了参数向量集合P，贝叶斯网络的构建就是找出一个最优的网络B=(G,P)，能够真实地反映现有数据集中各个变量之间的依赖关系[14]。

但是传统的静态贝叶斯网络的主要缺点是：①在样本量小时，很难从一个极为复杂的数据中得出最好的模型；②模型不允许循环(反馈环)结构的存在，因此无法描述X1→X2→X3→X1这样的环状反馈结构，但是在生物学过程中包含了很多这样循环调控过程，因而静态贝叶斯在构建网络结构上有着很大的限制[13]。为解决这一问题，提出了动态贝叶斯网络，动态贝叶斯网络是一般静态贝叶斯网络扩展时间维度的版本，即在原来网络结构上加上时间属性，并且很多静态贝叶斯算法的思想都可以沿用到动态贝叶斯网络的构建上[13,15]。构建动态贝叶斯网络一般分为三个步骤：

(1)确定需要分析的变量及其取值范围 由于贝叶斯网络方法需要计算整个网络的联合概率分布，在实际问题中变量数目往往较大，直接将所有变量纳入网络的构建，不仅会增加运算的复杂度，而且构建出来的网络模型过于复杂，变量间的相互作用无法解释，甚至由于混杂因素得出无法合理解释的生物学结构。因此在构建网络前，需要对变量进行变量筛选，根据研究目的选择有价值的变量构建网络模型，并确定这些变量的取值范围。

(2)确定网络结构 又称为结构学习(structure learning)，即通过给定的样本数据集进行学习，从中选出最能代表各变量关系的网络结构。贝叶斯网络的结构学习方法可分为基于约束算法和基于搜索得分算法，以及这两种算法的混合算法。基于约束算法通过条件独立性检验(conditional independence test)来判断变量间的依赖和独立关系。基于搜索得分算法则通过定义一个得分方程，用以评价不同网络结构对数据的拟合程度，得分越高，表示网络结构对数据拟合越好，选择得分最高的网络结构作为最佳网络结构。混合算法，即首先通过基于约束算法学习得出无方向的网络框架，然后利用搜索得分算法为网络中的边确定方向。

(3)确定局部概率分布 又称为参数学习(parameter learning)，指基于第二步确定的网络结构，对给定的样本数据进行学习，确定各节点处的局部条件概率。由于各节点加入了时间因素，在动态贝叶斯网络中节点的集合是包含时间因素的随机过程，需要得知每个随机变量Xi在各个时间点Xi,1,Xi,2,…,Xi,t上的概率分布。动态贝叶斯网络模型需要满足以下假设条件：

① 在一个有限时间内，所有时间点上的条件概率的变化过程一致。

② 动态概率过程依然满足马尔科夫条件，P(Xt+1|X1,X2,…,Xt)=P(Xt+1|Xt)，即未来时刻的概率只与当前时刻有关，而与过去时刻无关。

③ 相邻时间的条件概率过程是稳定的，即P(Xt+1|Xt)与时间t无关，因此可以得到不同时间的转移概率。

基于以上的假设，时间序列的动态贝叶斯网络可由两部分组成：①先验网络B0，用于定义初始时间(t=1)状态下X的联合概率分布；②转移网络B→，用于定义变量Xt与Xt+1上的转移概率P(Xt+1|Xt)。上述问题可以用图1表示。

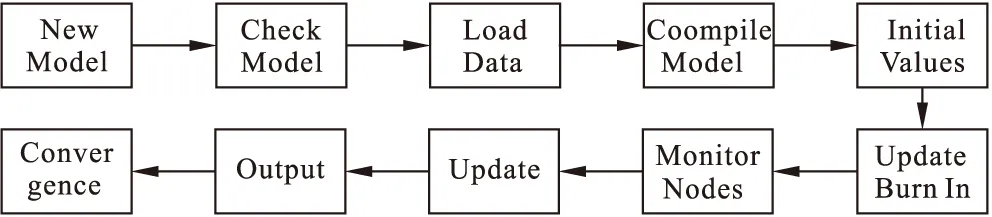
图1 动态贝叶斯网络示意图

动态贝叶斯网络模型的联合分布概率为

(4)

由于时间因素的引入，可将上述反馈调控机制做成图2中X1,t→X2,t+1→X3,t+2→X1,t+3形式的网络，从而解决静态贝叶斯网络无法处理的环路问题。同时，动态贝叶斯能够依据时间的先后顺序，揭示因果间关系，构建出的网络结构有更高的准确度。因此对于生物反馈调控网络，动态贝叶斯的还原能力优于静态贝叶斯。由于贝叶斯网络在网络的结构学习过程中，可以有效地结合先验知识，从而能够提高网络构建的准确性和运算速度，Whrhil和Husmeier等人利用生物学先验知识的基因表达数据，推断出了更为准确的基因调控网络[16]。Akutekwe 等人在构建出动态贝叶斯网络的结构基础上，结合支持向量回归方法中的非线性核函数来推断基因间的时序关系，在大肠杆菌和果蝇的基因调控网络中进行验证，并构建出与卵巢癌化疗敏感性相关的基因调控网络结构，识别出4个与卵巢癌化疗有关的中心调控基因[17]。

图2 动态贝叶斯网络对反馈调控

3.随机森林回归的网络构建方法

[3]王磊,姚骏.基于HTML5的移动病房WebApp的设计与实现[J].工业控制计算机,2017,30(05):143-144+148.

基于回归的网络构建方法，可以将p个基因的调控网络转化为建立p个回归模型的问题。线性回归模型不适合描述非线性调控关系，而且需要对变量的数目进行限制，而随机森林(random forest，RF)回归则更适合一般性的网络构建问题[18]。对于每个基因g，首先可以构建所有除去基因g本身以外的其他基因对基因g影响的回归模型，则第j个目标基因的回归模型可表示如下型式：

xj=fj(x-j)+εj

(5)

其中x-j=(x1,K,xj-1,xj+1,K,xp)，fj(x-j)为基于树给出的RF预测函数，εj表示误差项。随机森林回归算法中内嵌变量重要性排序机制，可得到目标基因与其转录因子间调控关系的大小，再把所有的调控关系合在一起进行排序，从而重建整个网络。

基于树集成的回归方法通过平均多棵树同时预测，极大地提高单棵树的预测性能。在随机森林中，每棵树的构建通过从原始训练集中抽取一个bootstrap样本得到，在每棵树的节点，从输入基因中选择k(k∈x-j)个基因作为此节点的备选分枝变量，然后根据分枝优度准则选取最优分枝。

基于树方法的随机森林回归，可以给出变量的重要性评分(variable importance measure,VIM)，其值可用方差改变量法计算，即对回归树的每个节点N，计算由于样本分裂导致的输出变量方差的总减小量，即

I(N)=#SVar(S)-#StVar(St)-#SfVar(Sf)

(6)

其中，S代表到达节点N的样本含量，St和Sf代表这些样本在节点N上分为两类的样本含量，即S=St+Sf，Var(·)表示不同数据中某变量的方差，#代表一组样本的数量。此方法计算的VIM值为某个变量在所有树中I值的平均值，即

(7)

由于不同基因表达值的数量级可能不同，在计算基因间VIM值前需要对数据进行标准化，以消除不同数量级的基因表达值对结果的影响。最后可以根据p个RF回归模型中的VIM值大小，确定其网络结构。

4.基于解卷积的网络优化算法

在构建网络的过程中，由于变量间关联的传递效应，现有的网络构建方法有时无法很好地识别出真正的调控关系，如在一个真实的网络中，节点1和节点2间存在强相关，节点2和节点3也存在强相关，那么节点1和节点3间也会存在较高的相关关系。即使节点1和节点3间并没有直接的调控关系，但是在网络结构推断过程中，节点1和节点3也容易被推断出一条边来。由于间接边的存在，两节点间的相关性也可能会被高估。随着网络规模的扩大，这种效应会被进一步放大，造成推断出来的网络结构既包含直接边，也包含了大量假阳性的间接边。网络解卷积算法可用来解决这一问题。

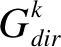
(8)

由实际数据获得的网络关联矩阵Gobs可做如下分解：

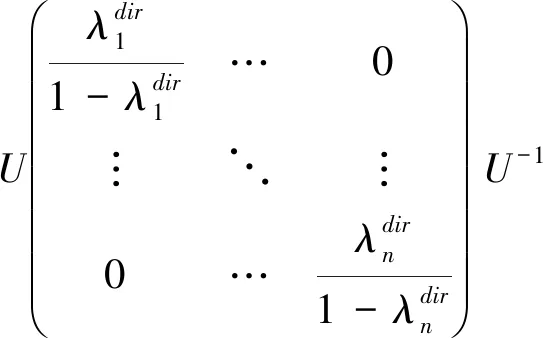
(9)

其中U代表特征向量，∑dir代表相应网络的特征值的对角矩阵。等式(a)利用网络邻接矩阵的特征值和特征向量分解原理；等式(b)利用泰勒级数得到。

同样，对于观察到的网络，可对其直接进行特征值和特征向量分解，即

(10)

将上述公式与等式(b)联立，可得到关于特征值的一个等式，即

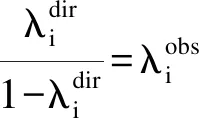
(11)

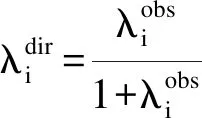
(12)

因此，由公式(12)，根据所求出的观察到的网络矩阵的特征值，可以求出直接相关网络的特征值，从而还原出直接网络结构Gdir。

网络解卷积算法假定网络的边权重满足2条线性关系假设：①间接边权重等于直接边权重的乘积；②观察到的边权重等于直接边和间接边权重之和。Feizi的研究表明[20]，该算法对于目前的一些网络构建方法都具有不同程度的优化作用，在DREAM5数据测验中进一步优化了由互信息算法，随机森林回归算法所构建的网络结构，使其准确度更高，挖掘到了更多有用的调控基因。

结 语

本文主要介绍了近年新发展的四种基因调控网络的构建方法。其中基于互信息的方法不需对变量间的关系做任何假设，因此能识别各种线性和非线性关系，但在计算互信息值时需要将数据离散化。动态贝叶斯网络，能够处理时间序列的基因表达数据，依据时间的先后顺序，揭示因果关系，使得还原的网络结构更容易解释。基于随机森林回归的算法，对网络的变量个数不需要限制，通过回归树对每个目标基因拟合回归模型，并通过集成树的多变量分析方法，计算出任意两个变量的关联性，结果相对稳健可靠。基于解卷积的网络优化算法则能够在满足假定条件下，对网络结构进行优化，移除由传递效应引起的间接边，准确地推断出直接边的网络结构。

实际上，基因调控网络的推断方法很多，仅用于DREAM5数据验证平台上的各种网络推断方法就有30余种。从基因表达水平的层面上，由于各基因间存在多种非线性调控关系，实际中可能需要结合多种网络构建方法进行分析。另外，如何利用适合的方法对不同层次(如基因和蛋白)的多组学数据构建网络，也极具挑战性。

[1]Smet DR,Marchal K.Advantages and limitations of current network inference methods.Nat Rev Microbiol,2010,8(10):717-729.

[2]刘万霖，李栋，朱云平,等.基于微阵列数据构建基因调控网络.遗传，2007,29(12)：1434-1442.

[3]Marbach D,Costello JC,Kuffner R,et al.Wisdom of crowds for robust gene network inference.Nat Methods,2012,9(8):796-804.

[4]Faith JJ,Hayete B,Thaden JT,et al.Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles.PLoS Biol,2007,5(1):54-66.

[5]Butte AJ,Kohane IS.Mutual information relevance networks:functional genomic clustering using pairwise entropy measuerments.Pac Symp Biocomput,2000,5:418-429.

[6]Margolin AA,Nemenman I,Basso K,et al.ARACNE:an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context.BMC Bioinformatics,2006,7(Suppl 1):S7.

[7]Daub CO,Steuer R,Selbig J,et al.Estimating mutual information using B-spline functions--an improved similarity measure for analysing gene expression data.BMC Bioinformatics,2004,5:118.

[8]Wang J,Chen C,Li HL,et al.Investigating key genes associated with ovarian cancer by integrating affinity propagation clustering and mutual information network analysis.European Review for Medical and Pharmacological Sciences,2016,20:2532-2540.

[9]Beirlant J,Dudewicz EJ,Gyorfi L,et al.Nonparametric entropy estimation:an overview.Intern J Math Stat Sci,1997,6(1):17-39.

[10]Mordelet F,Vert JP.SIRENE:supervised inference of regulatory networks.Bioinformatics,2008,24(16):i76-82.

[11]Ricardo A,Gerardo C,Karla L,et al.ARACNe-based inference,using curated microarray data of Arabidopsis thaliana root transcriptional regulatory networks.BMC Plant Biology,2014,14(97):1471-2229.

[12]Jang IS,Margolin A,Califano A.hARACNe:improving the accuracy of regulatory model reverse engineering via higher-order data processing inequality tests.Interface Focus,2013,3(4):20130011.

[13]强波，王正志.基于动态贝叶斯网构建基因调控网络.生物医学工程研究，2008，27(3)：145-149.

[14]Schafer J,Strimmer K.An empirical Bayes approach to inferring large-scale gene association networks.Bioinformatics,2005,21(6):754-764.

[15]赵红.利用动态贝叶斯网构建基因调控网络的研究进展.数学建模及其应用，2012，1(4)：5-11.

[16]Werhli AV,Husmeier D.Reconstructing gene regulatory networks with bayesian networks by combining expression data with multiple sources of prior knowledge.Statistical Applications in Genetics and Molecular Biology,2007,6(1):Art.15.

[17]Akutekwe A,Seker H.Inference of nonlinear gene regulatory networks through optimized ensemble of support vector regression and dynamic Bayesian networks.Conf Proc IEEE Eng Med Biol Soc,2015:8177-8180.

[18]Huynh-Thu VA,Irrthum A,Wehenkel L,et al.Inferring regulatory networks from expression data using tree-based methods.Plos one,2010,5(9):e12776.

[19]侯艳，杨凯，李康.基于随机森林回归的网络构建方法及应用.中国卫生统计，2015，32(4)：558-561.

[20]Feizi S,Marbach D,Medard M,et al.Network deconvolution as a general method to distinguish direct dependencies in networks.Nat Biotechnol,2013,31(8):726-33.

(责任编辑：郭海强)

*国家自然科学基金资助(81473072，81573256)；黑龙江省青年基金资助(QC2015098)

△通信作者：李康,E-mail:likang@ems.hrbmu.edu.cn